时间序列模型在流感预测中的应用

郑月彬，朱国魂,2

（1.桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004；2.昆士兰大学 信息技术与电子学院，澳大利亚 昆士兰州 4072）

传染病中流感是严重威胁人类健康的传染病。目前，预防和控制流感最有效的方法是接种流感疫苗，流感疫苗的有效性主要取决于能及时准确地使用与流感病毒匹配的流感疫苗。然而由于全球人口流动日益加快，传染性病毒可以很快地从一个地区通过飞行乘客传染到另外一个地区[1-3]。例如2018年12月份，山东共报告法定传染病30783例，死亡32人。其中，流行性感冒报告发病1659例，环比增多134%，报告死亡1人。因此，对于流感的预防是一项极为重要的研究工作[4-6]。

针对既往流感的一些预测精度较低、效果较差的问题，本研究以国家流感中心的数据为研究对象，整理了国内2012年第1周至2018年第48周的流感监测周报数据，根据国家流感中心的数据，利用ARIMA模型和Holt-Winters指数平滑模型分别对2018年第49周至2018年第52周的流感趋势进行预测。结果表明，对于流感趋势的预测，ARIMA模型相对于Holt-Winters指数平滑模型预测精度更高、预测效果更好，可用于对国内流感趋势的预测。

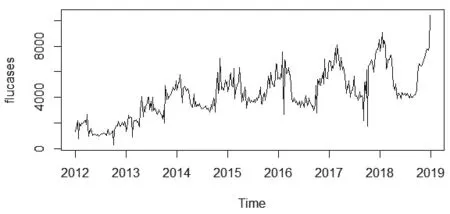
图1 国家流感中心2012年第1周至2018年第48周流感数据序列图Fig.1 Influenza data sequence map of the National Influenza Centre 2012 to the 48th week of 2018

1 材料与理论基础

1.1 数据

本研究所用数据来源于国家流感中心（http://www.chinaivdc.cn/cnic/），整理了国内2012年第1周至2018年第48周的流感监测周报数据，并将其形成时间序列，如图1所示。从图1可以看出，国内流感病例每年呈增长趋势，且每年的冬春交替时期是流感发病的高峰期，反映了对于流感的监测问题愈发严重，但对于流感的爆发，也是有律可循。

1.2 方法

自回归积分滑动平均模型（ARIMA模型）是时间序列分析模型中最为常用的模型之一，ARIMA模型原理主要是根据时间序列上的历史值及当前值实现时间序列上未来值的预测分析，能够不受其他相关变量变换的影响[7]。ARIMA模型的特点是必须应用于平稳时间序列，在应用ARIMA模型之前应对序列的平稳与否进行分析，对于不平稳时间序列数据需要进行d阶差分转化为稳定时间序列[8]。序列差分转换后为d阶单整序列，d为差分阶数，最后转换为平稳序列。ARIMA模型预测公式中p为时序数据本身的滞后数，即模型中的AR项；q为预测误差的滞后数，也称MA项，模型预测要首先确定p、q分别为AR和MA的系数。

Holt-Winters指数平滑模型是指数平滑法预测方法的一种，适用于具有增长或降低趋势，存在季节性[9]，并且可以用加法模型去描述的时间序列。Holt-Winters指数平滑法依靠其3个参数来估计当前时点的水平、斜率和季节性3部分。平稳的、趋势的和季节性的方程式中α用来估计当前时间的水平，β用于估计当前时间的趋势部分的斜率，γ用于估计当前时间的季节性部分。α、β、γ3个参数的取值范围相同，在0至1区间内，参数值越接近0，代表近期观测值对于未来的预测值权重越小，反之参数值越接近于1,则代表近期观测值对于未来的预测值权重越大[10]。

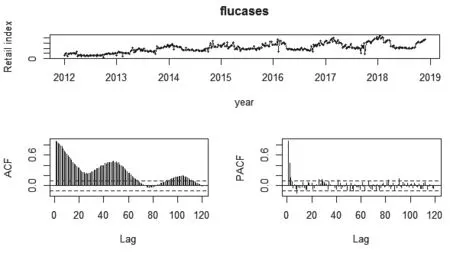
图2 原始序列检验图Fig.2 Original sequence test diagram

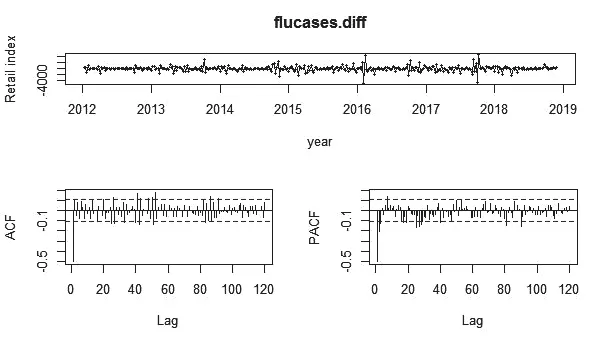
图3 一阶序列检验图Fig.3 1 Order Sequence inspection diagram

2 实验部分

ARIMA模型和Holt-Winters模型两者对所处理序列的平稳性要求有所不同，ARIMA模型只适用于平稳的时间序列，对不平稳的序列，应用ARIMA模型则需要进行平稳化处理，而Holt-Winters模型的应用则与序列的平稳性无关，无论序列平稳与否，皆可应用Holt-Winters模型。对本实验用到的国内2012年第1周至2018年第48周的流感监测周报数据的序列进行分析，图2表明序列自相关图呈拖尾性，若将ARIMA模型应用于此序列，则需对序列进行平稳化处理，序列自相关系数与偏自相关系数无季节跳跃，选择季节项系数为0。

因原序列为不平稳序列，所以对国内2012年第1周至2018年第48周的流感监测周报数据的序列进行一阶差分，并对差分后的序列进行分析，图3显示差分后的序列为平稳序列，且差分后自相关系数与偏自相关系数为0阶拖尾，故选择自相关系数与偏自相关系数均为0，ARIMA模型差分阶数为1，确定ARIMA最优模型为ARIMA(0,1,0)×(0,0,1)52。

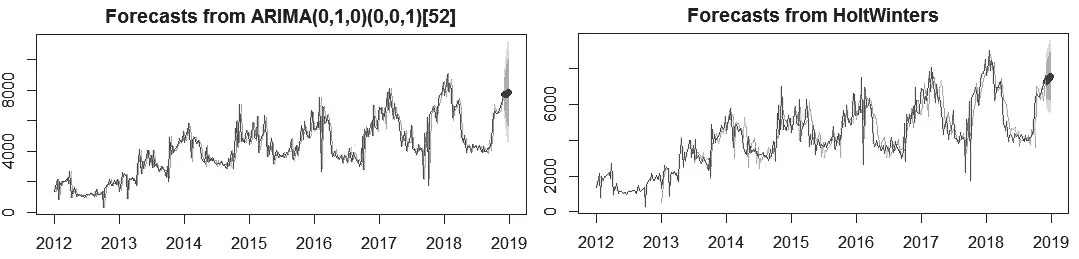
图5 预测结果对比图Fig.5 Comparison chart of forecast results

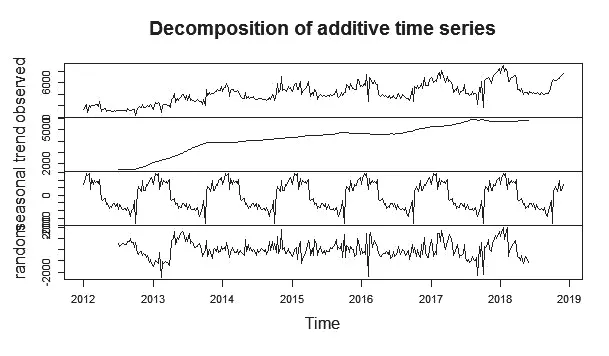
图4 原始序列分解图Fig.4 Original sequence decomposition diagram

Holt-Winters模型参数的选择依赖于对序列趋势、季节和随机波动部分的分解分析，对国内2012年第1周至2018年第48周的流感监测周报数据的序列进行相关的分解，结果见图4。原始序列、估计出的趋势部分和季节性部分及随机波动部分在图4中从上至下依次得出，观察分析国内2012年第1周至2018年第48周的流感监测周报数据的序列，可见其季节性部分具有明显的周期性波动。针对原始序列，Holt-Winters模型自定参数分别为α为0.45，β参数为0，γ参数为0.31，其参数均符合序列估计出的趋势部分和季节性部分及随机波动部分的趋势，所以Holt-Winters模型对国内2018年第49周至第52周序列值的预测选用系统自定参数。

3 结果

3.1 模型预测结果

对比观察ARIMA(0,1,0)×(0,0,1)52模型及Holt-Winters乘法模型对国内2012年第1周至2018年第48周的流感监测周报数据的序列值的预测，预测结果如图5所示。图中红色实曲线代表国内2012年第1周至2018年第48周的流感监测周报数据的历史数据，绿色曲线代表利用历史数据计算出来的2012年第1周至2018年第49周流感发病数量的历史数据拟合值，蓝色曲线代表2018年第49周至2018年第52周预测值，深灰色部分和浅灰色部分分别为80%和95%的置信区间。

将ARIMA模型和Holt-Winter乘法模型预测的序列值进行统计，并将ARIMA模型和Holt-Winter乘法模型预测结果与国家流感中心2018年第49周至2018年第52周流感发病数量实际值进行对比，对比结果见表1。ARIMA模型和Holt-Winter乘法模型预测结果对比明显，在所预测的4周中，ARIMA模型各周预测结果相比Holt-Winter乘法模型相对误差较小，预测精度较高。

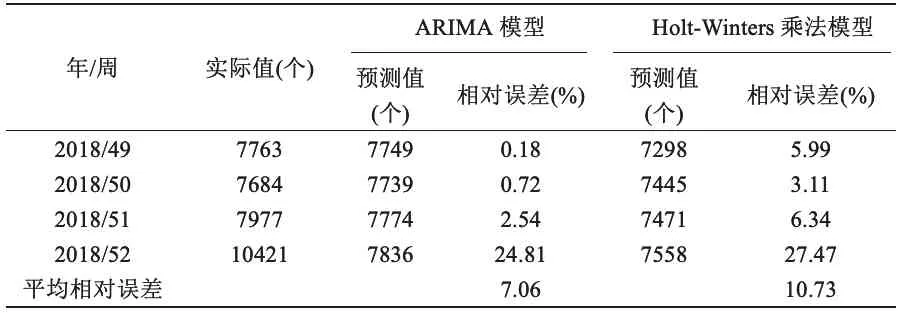
表1 ARIMA模型和Holt-Winter乘法模型预测误差对比表Table 1 Comparison table of prediction errors between Arima model and holt-winter multiplication model

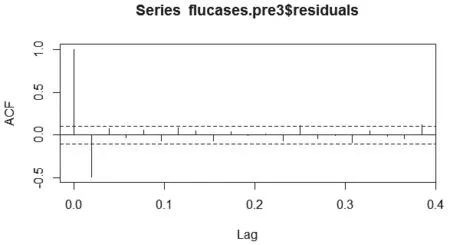
图6 ARIMA模型ACF检测结果图Fig.6 Arima Model ACF test results diagram

3.2 模型预测性能分析

为了验证模型的有效性，对ARIMA(0,1,0)×(0,0,1)52模型进行ACF自相关性检测，结果如图6所示。该模型的各阶残差自相关系数相关阶数内没有超过置信区间，说明ARIMA(0,1,0)×(0,0,1)52模型拟合之后的残差序列不存在自相关性。

对Holt-Winter模型进行Ljung-Box检验，检验结果中p-value为0.075，大于0.05的检验标准，表明该Holt-Winter模型可以通过白噪声检验，适用于对国内2012年第1周至2018年第48周的流感监测周报数据的序列建模。

4 结论

流感的爆发往往猝不及防，冬春换季流感更是严重，往往具有肆虐范围广、症状严重等特点，且儿童和老年人等弱势群体抵抗力差，通常成为流感爆发的重灾区，流感的盛行给人类的健康带来了严重的危害，对流感的预防监测课题也更加有意义。本文采用国家流感中心的数据进行流感爆发预测的研究，运用ARIMA模型和Holt-Winter乘法模型分别对国内2012年第1周至2018年第48周的流感监测周报数据的序列进行了建模，并对2018年第49周至2018年第52周的预测结果进行了分析和对比，结果如本文表1所示，Holt-Winters乘法模型和ARIMA模型在预测中的平均相对误差分别为10.07%和7.06%，预测结果表明ARIMA模型的预测相对误差小于Holt-Winters乘法模型。实验结果显示基于国家流感中心数据的ARIMA模型能够准确有效地监测国内流感趋势。