多波束声线跟踪改进模型研究与分析

刘 毅 ，王佑喜 ，周兴华

（1.浙江省河海测绘院，浙江 杭州 310008；2.浙江省河口海岸重点实验室，浙江 杭州 310020；3.浙江省水利防灾减灾重点实验室，浙江 杭州 310020）

1 问题的提出

在多波束测量过程中，声波在穿越不同水层时，不仅传播速度不同，还会发生声线弯曲现象。由于大量的非垂直入射的波束，若认为声线在整个水柱中按直线传播且声速值不变，采用三角法直接得到水底的坐标，其计算精度难以满足要求，声线的弯曲和声速的变化在很大程度上影响多波束测量成果的质量，是多波束系统的主要系统误差来源。为此，要想提高多波束测量成果的精度，在考虑声波的传播特性的基础上，研究一种声线跟踪技术，对测深数据进行补偿，以提高测深数据的精度，有着重要的理论和现实意义。

2 声速变化及声波传播特性对测深值的影响

2.1 声速变化对测深值的影响

海洋中的声速是一个比较活跃的海洋学变量，由于受到季节性变化和昼夜温差的影响，表层声速的变化是整个声速剖面变化中最活跃的部分，对测量精度影响最大，尤其是边缘波束，下面以表层声速为例进行分析。

表层声速对测深的影响包括2个方面，一是表层声速所造成的波束指向角误差，致使在波束脚印位置归算时造成的水深误差；二是表层声速误差在脚印位置归算时直接造成的误差。为更加直观的表现表层声速和波束指向角误差对测深精度的影响，令水深为100 m，系统声速为1 500.00 m/s，分别计算表层声速为1 400.00 m/s和1 600.00 m/s时，波束脚印位置的回波曲线（见图1）。

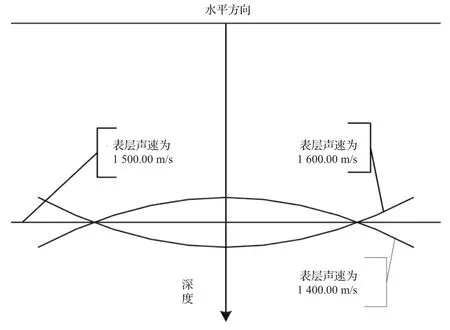
图1 回波曲线仿真示意图

当发射频率恒定时，若仪器设定的表层声速小于实际表层声速，仪器设定的波束指向角小于实际的波束指向角，则波束覆盖面积变小，水深在中央部分测深，在边缘部分测浅，形成笑脸状失真；若仪器设定的表层声速大于实际表层声速，仪器设定的波束指向角大于实际的波束指向角，则波束覆盖面积变大，水深在中央部分测浅，在边缘部分测深，形成哭脸状失真。

2.2 声波的传播特性对测深值的影响

声波在2种介质的界面上或同种介质发生变化时会发生折射和反射，符合折射、反射定律，满足Snell法则。Snell法则可表述为：

式中：θi、θi+1是声速为Ci和Ci+1相邻介质层界面处波束的入射角和折射角（°）；p为Snell常数。

根据Snell法则，声波在传播的过程中遇到不同介质层将发生折射，这将使各波束声线的旅行路径和前进方向发生改变，造成声线弯曲现象。声线弯曲对测深影响示意见图2。从图2可以得出，声线弯曲对多波束测深的影响主要反映在2个方面：一是对声线传播距离的影响，也就是对覆盖宽度的影响；二是对水深测深值的影响。

图2 声线弯曲对测深影响示意图

3 声线跟踪计算原理

根据Snell法则，若表层声速C0和声速C(z)的垂直分布已知，则可以按式（1）解算海洋中任意深度处声线的入射角，从而可确定任意深度声波的传播方向。对于恒定声速梯度，若声线在海面以θ0为入射角入射，且声源位于y =0，z = z1处，接收点位于(y，z )点处，声速按c = c(z)分布，可以采用下列积分来求出声线经过的水平距离：

根据Snell法则可导出：

式中：n表示折射率，即n = C(z1)/C(z)。对于恒定声速梯度情况，轨迹是一弧线。有时，直接从声线轨迹图来求水平距离更为方便，其基本关系式为：

式中：g为绝对声速梯度，g = dC/dz = C0θ。

4 声线跟踪建模分析

声线跟踪技术是建立在声速剖面基础上的一种波束脚印相对船体坐标的计算方法。即将声速剖面内相邻2个声速采用点划分为1层，层内声速变化可假设为常值或常梯度。在实际海底测量过程中，可以将测得声信号从发射到达海底的往返时间为T。声线跟踪的基本思想就是用声波单程旅行时间减掉声线在每层传播所用的时间，一直减到0为止。此时，声线的终点就是声线到达海底的实际位置。

4.1 常声速 — 声线跟踪模型

假设波束经历由N层组成的水柱，声速在层内以常速传播（即声速梯度为0）（见图3），根据Snell法则：

图3 常声速声线跟踪示意图

设层厚度为Δzi（Δzi= zi+1- zi），则波束在i层内的水平位移yi和传播时间ti为分别为：

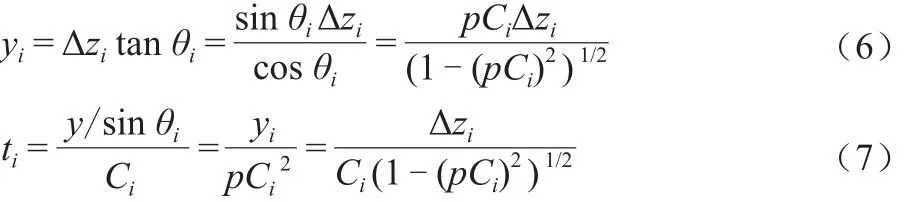
根据式（6）及式（7），波束经历整个水柱的水平距离和传播时间分别为：

4.2 常梯度 — 声线跟踪模型

假设波束经历由N个不同介质层组成的水柱，声速在各层中以常梯度gi变化，声速变化函数采用Harmonic平均声速。

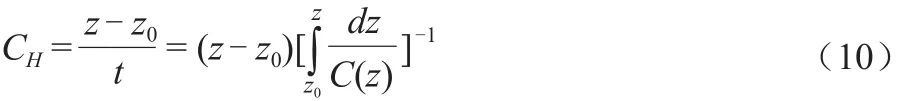
常梯度声线跟踪示意见图4。

图4 常梯度声线跟踪示意图

如图4所示，设层i上下界面的深度分别为zi和zi+1，i层的厚度为Δzi，波束在层内的实际传播轨迹应为1条连续的、有一定曲率半径的弧段，设其曲率半径为Ri：

则层内声线的水平位移yi为：

由式（5）可知：cos θi= (1 - (pCi)2)1/2（13）

且 Δz = z - z，则：

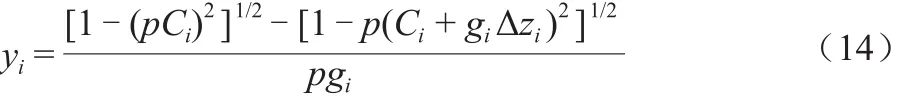
由图4可知，波束在该层经历的弧段长度Si= Ri(θi-θi+1) ，则经历该段的时间ti为：

4.3 常声速 — 声线跟踪改进模型

在传统的声线跟踪模型中，采用实测声速剖面在很大程度上考虑到声速误差对测深成果的影响，然而实测声速剖面与真实声速剖面仍然存在一定差异，特别是采用较粗的分层且采用常声速法时，声线跟踪模型受到声速误差的影响，模型本身存在较大误差。因此，在采用声线跟踪模型对多波束测深值进行改正时，还必须考虑声速误差的存在。设层内的声速为Ci其误差为dCi，以常声速 — 声线跟踪模型为例，它对层内折射角的影响为：

则式（8）、式（9）考虑声速误差的影响：

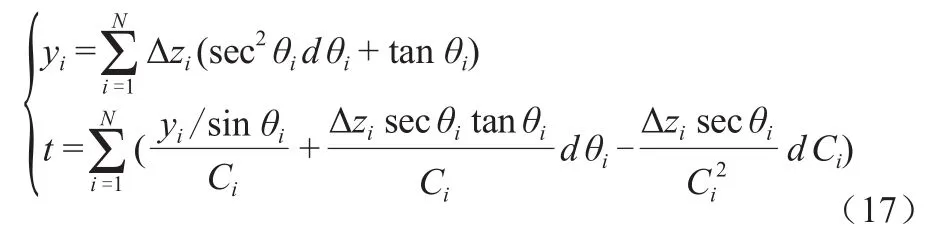
值得说明的是，在分层很细时采用常梯度法，每层中的声速变化不大，且用梯度变化来模拟声速的变化，因此，可以不对模型中的声速误差进行修正。

5 试验与分析

为了验证上述几种声线跟踪模型的正确性及可行性，利用某海域多波束测深数据进行声速改正试验。实测声速剖面见图5，最大深度为72 m，平均声速为1 449.98 m/s。由于声速误差和声线弯曲现象的存在，实际测得的水深值存在系统误差，不能作为评价精度的标准。在计算深度相对误差时，依据实际声速剖面，采用精细分层的常梯度 —声线跟踪法计算得到深度值作为水深真值Z。

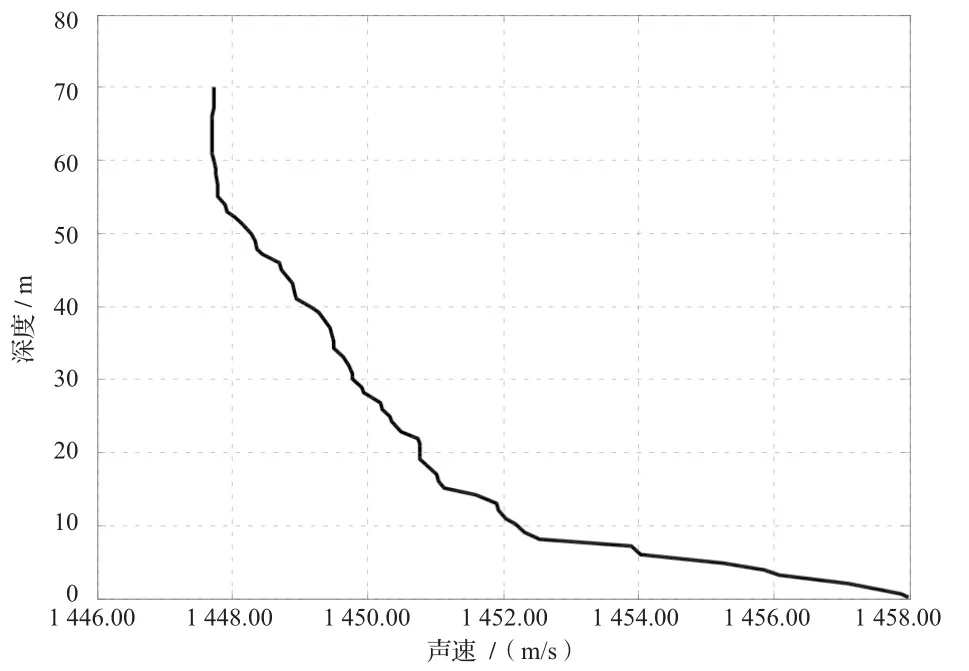
图5 实测声速剖面图

声线跟踪模型主要有层内声速变化假设为常值的常声速 — 声线跟踪法和层内声速变化假设为常梯度的常梯度 —声线跟踪法，以及本文提出的改进模型。为比较3种方法的计算精度，分别采用1 m分层和7 m分层对3种模型进行计算，其中改进模型是基于常声速模型进行计算的。声线跟踪模型的比较计算结果见表1、表2，声线跟踪模型的计算精度见图6。

表1 声线跟踪模型比较表 （1 m分层）

表2 声线跟踪模型比较表 （7 m分层）

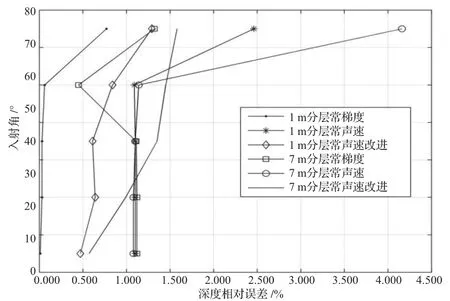
图6 声线跟踪模型的计算精度图

从表1、表2和图6可以得出，声线跟踪模型的深度相对误差远小于IHO规定的4z‰的精度指标，而且分层越细精度越高，常梯度 — 声线跟踪的模型精度优于常声速 —声线跟踪模型，主要是在每层计算中严格参考实际声速剖面的测量参数，并采用常梯度的方式来模拟声速变化，其计算精度优于z‰。常声速 — 声线跟踪模型，虽然顾及声速剖面，但未严格地考虑声速在每层中的实际变化规律，在入射角小于60°时，具有较高精度。基于常声速的改进模型，计算精度比常声速模型明显提高，在入射角小于60°时，已接近常梯度模型计算精度。在实际应用中，对于波束覆盖较小的多波束设备，使用较粗的声速分层，3种声线跟踪模型都具有较高的精度；对应波束覆盖较大的设备，采用常梯度 — 声线模型和改进模型进行声速改正均有较好的效果。

6 结 语

声速改正在多波束数据处理中十分重要，同时也极难控制，声线跟踪法对实测声速剖面依懒性较强，在生产实践中，声速剖面站不可能将整个测区覆盖，其代表性误差对声速剖面有一定的影响，在海况复杂的情况下，这种影响较大。精细分层下的常声速声线跟踪改进模型虽然计算相对简单，但对于边缘波束，深度相对误差较大。因此，一种不依赖声速剖面而能满足精度要求并且计算简捷的声速改正方法还需进一步研究。