一类函数的零点与导数问题

■河南省西华县第一高级中学 李松林

与极值点偏移问题类似，函数的零点问题也成为高考考查的热点，大部分同学处理时感到非常棘手，尤其是当出现两个零点x1与x2的关系转化时，显得更加吃力。下面就x1与x2的关系转化方案即多元问题的转化，进行初步探索。

一、由题中的要证结论把x1与x2变换为然后进行换元构造函数

例1 已知函数f(x)=2x(l nx+1)。

(1)求函数f(x)的单调区间；

(2)若斜率为k的直线与曲线y=f "(x)交于A(x1，y1)，B(x2，y2)两点，其中x1＜x2，求证

分析：此题主要考查导数的应用，导数与单调性的关系及函数的零点问题，并且牵涉两个零点的处理方法，要尽量把两个零点x1与x2进行转化，使未知参数尽可能减少。

解：(1)函数的定义域为(0，+∞)，f "(x)=2(l nx+1)+2=2 l nx+4=2(l nx+2)。令f "(x)＞0，得；令f "(x)＜0，得0＜。所以函数f(x)在区间上是减函数，在区间上是增函数。

(2)由已知得：

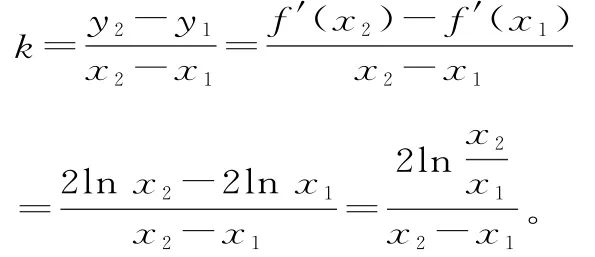
设g(t)=t—1—l nt，则g "(t)=1—，可得g(t)=t—1—l nt在区间(1，+∞)上是增函数。又g(1)=0，所以g(t)=t—1—l nt＞0，即l nt＜t—1。又设h(t)=tl nt—t+1，则h "(t)=l nt+t·1=l nt＞0，所以h(t)=tl nt—t+1在区间(1，+∞)上是增函数。又h(1)=0，所以h(t)=tl nt—t+1＞0，即t—1＜tl nt，所以l nt＜t—1＜tl nt(t＞1)成立，即成立，所以

方法总结：关键是把要证结论中的k利用x1，x2来表示，问题转化为含x1，x2的式子处理。

二、根据题中的条件得到两个零点x1与x2的关系式，然后化为的形式

例2 已知函数f(x)=al nx—b x2的图像上一点P(2，f(2))处的切线方程为y=—3x+2 l n2+2。

(1)求a，b的值；

(2)若方程f(x)+m=0在区间内有两个不相等的实数根，求实数m的取值范围；

(3)令g(x)=f(x)—k x，如果g(x)的图像与x轴交于A(x1，0)，B(x2，0)(x1＜x2)两点，且A B的中点为C(x0，0)，求证：g "(x0)≠0。

解析：(1)函数的定义域为(0，+∞)，因为f "(x)=—2b x，所以f "(2)=—3，f(2)=al n2—4b=—4+2 l n2，可得a=2，b=1。

令f "(x)＞0得0＜x＜1，令f "(x)＜0得x＞1，所以函数f(x)在区间(0，1)上是增函数，在区间(1，+∞)上是减函数。所以y=f(x)+m的最大值为f(1)+m=—1+m。又当x→0时，y→—∞，当x→+∞时，y→—∞。所以若方程f(x)+m=0在区间内有两个不相等的实数根，则必有解得1＜

方法总结：解决此题的关键在于：①根据函数f(x)的零点，建立x1与x2的关系式；②用反证法得到含有x1与x2的等式；③变形为的式子，然后换元构造函数。

三、通过放缩变换得到x1与x2的关系，消去多余的变量，化多元为一元

例3 已知函数f(x)=x—as i nx(a＞0)。

(1)若y=f(x)在R上单调递增，求实数a的取值范围；

解析：(1)f "(x)=1—ac o sx，因为f(x)在R上单调递增，所以f "(x)=1—ac o sx≥0恒成立，所以ac o sx≤1，即≥c o sx。因为c o sx∈［ — 1，1］，所以≥1。又因为a＞0，所以0＜a≤1。

由已知g(x1)=g(x2)(x1≠x2)，可得

由(1)知f(x)=x—sinx在R上单调递增，不妨设x1＜x2，则f(x1)＜f(x2)，即x1—sinx1＜x2—sinx2，所以x1—x2＜sinx1—sinx2，则sinx2)，所以 —(x—x)，所以x—x—1212，即＞0，所以bl n

因为x1＜x2，所以l n＜0，所以b＜，所以x1x2＜4b2⇒＜—2b。

又因为 —2b＞，所以只需证，只需证

令h(t)=—l nt(0＜t＜1)，则h "(t)

所以h(t)=—l nt在(0，1)上是增函数，且h(1)=0，所以h(t)=0，即＜l nt成立，所以x1x2＜4b2得证。

方法总结：解决问题的关键在于根据第(1)问的结论，通过放缩消去(sinx1—sinx2)，从而转化为x1—x2，得到x1与x2的关系，再由结论进行放缩转化为的形式，进而换元，构造函数。