函数及导数应用易错题归类剖析

■河南省许昌高级中学 杨 涛

“函数与导数”是高中数学中的重点和难点知识，在历年高考中都占据着重要的地位，而且这部分知识既有难度较大的填空题，还有计算烦琐的解答题。又因为“函数”贯穿高中数学的始终，因此，学好这部分知识对同学们来说，显然是非常必要的。鉴于这部分知识有很多易错点，笔者根据自己的教学实践，对这部分知识的易错点总结剖析如下，供同学们参考。

易错点一：概念的理解不到位

在“函数”的学习中，经常会遇到一些条件相似，但在本质及解题方法上却存在很大差异的问题。若能及时对它们进行对比、区别，则可摆脱知识的“负迁移”，走出思维的误区，提高解题的准确率，同时对同学们加深对概念的理解、题意的挖掘、审题能力的培养等方面都大有益处。

1.定义域与值域。

例1 (1)若函数y=l g(x2+x+2a)的定义域为R，求实数a的取值范围；

(2)若函数y=l g(x2+x+2a)的值域为R，求实数a的取值范围。

分析：这两小题都属于恒成立问题，但仅一字之差，表达的含义却截然不同。第(1)问中要求函数u=x2+x+2a的值域为正实数集的子集，而第(2)问中则要求函数u=x2+x+2a必须取到一切正数。平时学习中第(1)问的情形较常见，解答第(2)问时，因受第(1)问的影响极易出现错误。因此，审题时应善于找出题组间含义的相异之处。

解：(1)依题意，x2+x+2a＞0对一切x∈R恒成立，故Δ=1 2—4×1×2a＜0，解得a＞1 8。

(2)依题意，x2+x+2a能取遍正实数集内的所有实数值即可，即要求正实数集为函数值域的子集，故Δ=1 2—4×1×2a≥0，解得a≤1 8。

2.主元与参数。

例2 (1)已知函数f(x)=x2+a x+1，在x∈[0，2]上，f(x)＞0恒成立，求实数a的取值范围；

(2)已知函数f(x)=x2+a x+1，当a∈[0，2]时，f(x)＞0恒成立，求实数x的取值范围。

分析：在同一题目中，主元与次元是相对的，只有合理区分主元与次元，才能快速解题。

解：(1)将“x”看成主元，“a”看成参数。

①当x=0时，f(x)=1＞0恒成立，此时a∈R；

②当x∈(0，2]时，x2+a x+1＞0恒成立，即a＞又因为≤—2(当且仅当x=1时取等号)，故a＞—2。

综上，实数a的取值范围为(—2，+∞)。

(2)将“x”看成主元，“a”看成参数。f(x)=g(a)=x2+a x+1＞0恒成立，应有g(0)＞0，g(2)＞0，即x2+1＞0，x2+2x+1＞0，解得x≠—1。故实数x的取值范围为(—∞，—1)∪(—1，+∞)。

易错点二：过点P的切线与在点P处的切线

过一点求曲线的切线方程有三种不同的类型，下面举例说明。

1.已 知 曲 线y=f(x)上 一 点P(x0，f(x0))，求曲线在该点处的

这是求曲线的切线方程的基本类型，课本上的例、习题都是这种类型。其求法为：先求出函数f(x)的导数f "(x)，再将x0代入f "(x)求出f "(x0)，即得切线的斜率，然后写出切线方程y—f(x0)=f "(x0)(x—x0)，化简整理即可。

例3 求曲线f(x)=x3—3x2+3在点P(1，1)处的切线方程。

解析：由题设知点P在曲线上，因为f "(x)=3x2—6x，所以曲线在点P(1，1)处的切线的斜率为f "(1)=—3，故所求的切线方程为y—1=—3(x—1)，即y=—3x+4。

2.已知曲线y=f(x)上一点A(x1，f(x1))，求过点A的曲线的切线方程。

这种类型容易出错，一般学生误认为点A一定为切点，事实上可能存在过点A而点A不是切点的切线，要引起注意，这类题型的求法为：设切点为P(x0，f(x0))，先求出函数f(x)的导数f "(x)，再将x0代入f "(x)求出f "(x0)，即得切线的斜率(用x0表示)，写出切线方程y—f(x0)=f "(x0)(x—x0)，再将点A的坐标(x1，y1)代入切线方程得y1—f(x0)=f "(x0)(x1—x0)，求出x0，最后将x0代入方程y—f(x0)=f "(x0)(x—x0)，求出切线方程。

例4 求过曲线y=x3—2x上的点(1，—1)的切线方程。

解析：设切点为(x0，—2x0)，因为y "=3x2—2，所以切线斜率为3—2，故切线方程为y—(—2x0)=(3—2)(x—x0)。

又知切线过点(1，—1)，把它代入上述方程，得—1—(—2x0)=(3x0—2)(1—x0)，解得x0=1，或

故所求切线方程为y—(1—2)=(3—2)·(x—1)，或，即x—y—2=0，或5x+4y—1=0。

上面所求出的两条直线中，直线x—y—2=0是以(1，—1)为切点的切线，而切线5x+4y—1=0并不是以(1，—1)为切点，实际上它是经过了点(1，—1)且以为切点的直线，如图1所示。这说明过曲线上一点的切线，该点未必是切点。

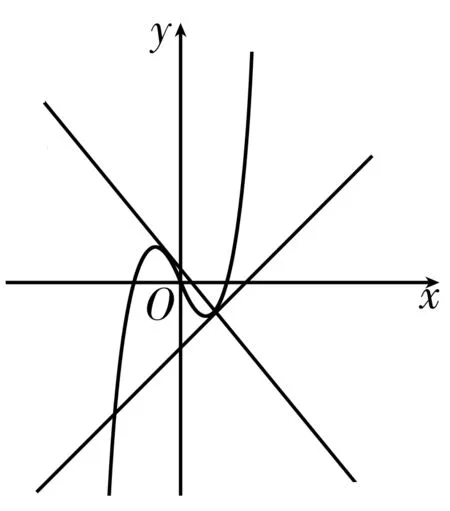
图1

3.已知曲线y=f(x)外一点 A(x1，f(x1))，求过点A的曲线的切线方程。

这种类型的题目的解法同上面第二种类型。

例5 过原点O作曲线y=x4—3x2+6的切线，求切线方程。

解析：由题设知原点O不在曲线上，设切点坐标为6x，切线斜率为4—6x0，切线方程为y—

故所求切线方程为y=—2x或y=2x。

易错点三：“导数值的符号”与“函数单调性”

设函数f(x)在某个区间内可导，若在此区间f "(x)＞0恒成立，则f(x)在此区间内单调递增；若在此区间f "(x)＜0恒成立，则f(x)在此区间内单调递减。利用导数解决函数的单调性问题时，除了掌握以上依据，还应明确以下几点(以增函数为例来说明)：

(1)f "(x)＞0是可导函数f(x)在定义域内单调递增的充分不必要条件。例如，函数f(x)=x2在区间(—∞，+∞)上单调递增，但f "(x)≥0。

(2)f "(x)≥0是可导函数f(x)在定义域内单调递增的必要不充分条件。若f(x)为增函数，则一定有f "(x)≥0，但反之不一定成立。因为f "(x)≥0为f "(x)＞0或f "(x)=0两者之一成立即可。当函数在某个区间内恒有f "(x)=0，则f(x)为常数，函数不具有单调性。

(3)f "(x)≥0且f "(x)在定义域内的任意子区间不恒为0是可导函数f(x)在定义域内单调递增的充要条件。

例6 已 知 向 量a=(x2，x+1)，b=(1—x，t)，若函数f(x)=a·b在(—1，1)上是增函数，求t的取值范围。

错解：因为f(x)=a·b=—x3+x2+t x+t，所以f "(x)=—3x2+2x+t。因为f(x)在(—1，1)上是增函数，则在(—1，1)上可得f "(x)＞0。因为f "(x)的图像是开口向下的抛物线，所以当且仅当f "(1)=t—1＞0且f "(—1)=t—5＞0时，f(x)在(—1，1)上满足f "(x)＞0，即f(x)在(—1，1)上是增函数，故t的取值范围是(5，+∞)。

评析：忽视特殊点f(x)=0。当f(x)在某个区间内的个别点处为零，其余点处为正(或负)时，f(x)在这个区间上仍然是单调递增(或递减)函数。例如，在(—∞，+∞)上，f(x)=x3，当x=0时，f "(x)=0，当x≠0时，f "(x)＞0，而f(x)=x3在(—∞，+∞)上显然是增函数。

正解：因为f(x)=—x3+x2+t x+t，所以f "(x)=—3x2+2x+t。由于函数f(x)在(—1，1)上是增函数，故在(—1，1)上可得f "(x)≥0恒成立。因为f "(x)的图像是开口向下的抛物线，所以当且仅当f "(1)=t—1≥0且f "(—1)=t—5≥0时，f(x)在(—1，1)上满足f "(x)≥0，即f(x)在(—1，1)上是增函数，故t的取值范围是[5，+∞)。

一个可导函数在某点处的导数为0是在该点取极值的必要不充分条件，即可导函数在某处取得极值，则函数在此处的导数值必等于0；反之，若在某处的导数值为0，则函数在该处不一定取得极值，还需进一步检验f "(x)在f "(x)=0处的根的左右两边的导数值的符号是否异号。

易错点四：“极值点”等同于“导数的零点”

对于满足f "(x0)=0的点x0称之为导数的零点，f(x)可导时f "(x)=0的点只是f(x)的极值点的必要不充分条件，所以把“极值点”等同于“导数的零点”容易出现错误。

例7 已知函数f(x)=在x=1处取得极值，且函数g(x)=—a x在区间(a—6，2a—3)上是减函数，求实数a的取值范围。

错解：由已知得f "(x)=x3+b x2—(2+a)x+2a，由f "(1)=0得b=1—a。

由已知得g "(x)=x3+b x2—(a—1)·x—a=x3+(1—a)x2—(a—1)x—a=(x—a)(x2+x+1)。

因此，当x＜a时，g "(x)＜0，即函数g(x)在(—∞，a)上单调递减。由(a—6，2a—3)⊆(—∞，a)，得a—6＜2a—3≤a，故所求a的取值范围为—3＜a≤3。

评析：以上解法忽略了一个细节，解题中用到f "(x)=0，即x=1是导数为0的点，那么x=1是不是函数的极值点呢?当b=1—a时，f "(x)=x3+b x2—(2+a)x+2a=(x—1)(x+2)(x—a)。如果a=1，那么x=1就只是函数f(x)的“拐点”而非极值点。由条件知f(x)在x=1处取得极值，因此应排除a=1，从而实数a的取值范围应是—3＜a＜1或1＜a≤3。

总之，同学们出现这些错误，一方面，是由于概念本身的抽象性，对基础知识掌握不全面或对题意理解不准确等导致的；另一方面，是因为教材对导数研究函数性质要求不全面、不太高，且教材选择的案例又太常规、太特殊，而平时遇到的函数丰富多样，所以同学们会出现认知盲点，出现错误。在平时的学习中，我们应该正视错误，剖析错误，澄清错误，对比分析，从而加深对概念本质的理解，消除疑惑，化解盲点，从而真正提高自己解决“函数与导数”问题的能力。