基于精细复合多尺度熵与支持向量机的睡眠分期

叶 仙， 胡 洁， 田 畔， 戚 进， 车大钿， 丁 颖

(1. 上海交通大学 机械与动力工程学院， 上海 200240； 2. 上海市儿童医院， 上海 200240)

人类1/3的时间都在睡眠中度过.与睡眠相关的疾病，如睡眠呼吸暂停以及低通气等睡眠障碍严重地影响了患者的生活质量.调查显示[1]，超过2%的成年女性以及4%的成年男性患有阻塞型呼吸暂停.在睡眠疾病的研究中，睡眠分期是必不可少的关键步骤.临床上按照Rechtchaffen and Kales(简称R&K)分期准则[2]将睡眠过程分为清醒期(W)、非快速眼动期(N)和快速眼动期(R).N期又被分为非快速眼动1期(N1)、非快速眼动2期(N2)、非快速眼动3期(N3)和非快速眼动4期(N4)，其中N3和N4通常被整合成深睡眠期.医疗人员根据美国睡眠医学会(AASM)标准[3]，通过观察α节律波、纺锤波和K复合波等特征来判别睡眠阶段.人的整夜睡眠时间为7～8 h，人工进行睡眠分期通常需要花费 2～4 h，并且不同专家的判读结果一致度低于90%.针对人工睡眠分期效率低、准确性不高的问题，研究人员提出采用自动区分睡眠过程的方法代替传统的经验判读方法.

睡眠分期主要包含睡眠信号(1帧图像)的特征提取以及睡眠时段的分类.睡眠信号的特征提取方法主要包括时域分析、频域分析、时频分析[4]和复杂性分析等方法.其中，复杂性分析方法是通过表征系统的动态特性来研究信号内在特征的，已经成为生物信号时间序列的研究方向.熵作为表征系统复杂度的重要指标，可用于区分人体生理信号的复杂度.Costa等[5]提出多尺度熵(MSE)方法，通过粗粒化的方式对时间序列进行多尺度划分，以实现对时间序列的多尺度分析.MSE方法能够分析时间序列隐藏在不同尺度的模式信息，但在多尺度样本熵粗粒化序列的研究中，基于粗粒化定义的多尺度计算方法对时间序列长度的依赖性较强.对于生理信号中的常见噪声(白噪声和1/f噪声)，当时间尺度增加时，所得到的时间序列越短，MSE与复合多尺度熵(CMSE)算法引入未定义熵的可能性越大，从而导致算法的有效性降低.在另一方面，睡眠分期的分类算法也存在差异性.Flexer等[6]采用隐马尔可夫方法(HMM)进行睡眠分期，其准确率达到了 80.0%；李谷等[7]利用希尔伯特-黄变换方法对睡眠进行自动分期，其平均准确率为 81.7%.近年来，研究人员提出了基于决策树的多分类支持向量机(SVM)算法[8]，并将其用于睡眠分期的多分类问题.

本文通过改进CMSE算法，提出了基于精细复合多尺度熵(RCMSE)的睡眠分期算法.对于较短的生物信号时间序列，当使用RCMSE算法时引入未定义熵的概率降低，所以RCMSE算法的有效性和准确性优于MSE以及CMSE算法，并且选择特征区分度较高的RCMSE特征作为分类器的输入，以保证输入的稳定性.另外，结合层次结构以及SVM的优势，利用多层次的SVM分类器进行睡眠分期，达到了快速准确的分期效果.

1 RCMSE算法

睡眠分期算法的流程如图1所示.首先，以30 s记录1帧图像，对睡眠的脑电(EEG)信号以及眼电(EOG)信号进行分段，并且对原始信号进行滤波处理；然后，对睡眠信号的复杂度进行分析，提取分类器的输入特征，即RCMSE；最后，运用多层次的SVM来实施睡眠分期.

图1 睡眠分期算法流程Fig.1 Flow chart of the proposed sleep scoring method

1.1 信号的提取与预处理

本文所用数据来源于美国生理信号数据库PhysioBank[9]中的Sleep-EDF数据库，选择10位健康成人作为研究对象，并对每位研究对象睡眠阶段的生理信号的记录时间为20 h，选用熄灯以后其EEG(Fpz-Cz)和EOG通道的波形作为研究信号.其中，选择对象的睡眠状态良好、各个睡眠时期已被完整地标注.整夜的多导睡眠图(PSG)包含Fpz-Cz通道和Pz-Oz通道的EEG信号、EOG信号以及肌电(EMG)信号.采集数据的幅值单位为μV，EEG信号以及EOG信号的采样频率均为100 Hz.EEG信号与EOG信号包含大量的生理信息，本文选取EEG(Fpz-Cz)和EOG通道的信号进行分析.

根据睡眠分期的判读规则，睡眠监测开始后，按照每30 s记录的1帧图像[10]进行判读.由于EEG信号和EOG信号的频率均为100 Hz，所以以 3 000 个样本点为1段对数据进行预分割.睡眠时，EEG信号极其微弱，背景噪声较强，易于引入干扰，如面部肌肉以及眼球的移动等；并且EEG信号和EOG信号均是非平稳的随机信号，难以提取特征，因此，需要利用有效的手段对其进行降噪处理.根据AASM推荐的各通道滤波标准，EEG信号及EOG信号的带通滤波标准均为 0.3～35.0 Hz，因此，设置巴特沃斯滤波器的通带频率为 0.3～35.0 Hz，以对信号进行滤波处理.

1.2 精细复合多尺度熵特征提取

本文以生物信号的复杂度作为睡眠分期的判定标准.目前，复杂度的量化方法包括近似熵[11]、样本熵、多尺度样本熵和RCMSE等.由于RCMSE的有效性及准确性较高，所以本文利用RCMSE方法分析睡眠信号的时间序列复杂度，计算EEG信号以及EOG信号的多尺度熵.以下为RCMSE算法的步骤.

(1) 采集研究对象的EEG和EOG信号，每一通道的信号为一维的离散时间序列.令x={x1,x2,…,xN}为长度为N的时间序列.粗粒化过程如下：

(1)

式中：1≤j≤N/τ，τ为尺度值；1≤k≤τ.

通过式(1)可以得到不同时间尺度上的粗粒化时间序列.

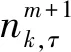
(2)

式中：

式(2)可简化为

(3)

通过考虑多方面的因素来选择合适的参数.其中：嵌入的维数m越大，包含的细节信息越多，但m值越大，需要的数据长度越长，综合考虑，本文选取m=2[12]；r值一般为原始数据标准差b的 0.10～0.25 倍，本文选取r=0.15b；由于选择太大的τ值将会影响计算效率，而选择太小的τ值将导致无法提取足够多的有效信息，因而本文设置粗粒化的最高τ值为20.

1.3 多层次支持向量机分类器设计

本文使用SVM方法进行模式分类.从本质上来说，SVM是一种二分类的方法.假设{(xi,yi),i=1,2,…,N}为训练集，其中xi∈Rd是输入数据，yi∈{-1,+1}为分类的标签，分别代表不同的睡眠状态.将超平面定义为

wTx+b=0

其中：w是d维的向量；b是标准偏差.为获得更大的边界以及更强的泛化能力，引入正的松弛变量ξi.根据以下约束的二次优化问题的求解来确定最优的超平面：

(4)

使得

yi(wTxi+b)≥1-ξi,i=1,2,…,N

(5)

式中：C是惩罚参数.通过求解优化问题来估计w和b.然后，定义离散决策函数，对输入数据进行分类：

(6)

式中：αi是拉格朗日乘子；K(xi,xj)=φ(xi)φ(xj)，为核函数，φ(x)为非线性函数，形成从训练数据到高维特征空间的映射.

图2 多层次SVM分类算法框图Fig.2 Block diagram of the proposed multi-classification SVM

本文的研究目标是将睡眠阶段分为5个不同的时期，即W期、N1期、N2期、N3期和R期，该分期属于多分类问题.针对睡眠分期的多分类问题[13]，一般采用将多分类问题转化为两分类问题来求解.具体方法：① 一对一法，即在每两类之间训练一个分类器.对于一个k类问题，存在k(k-1)/2个分类函数.② 一对多分类法，在每一类别与其他类别之间构造分类函数(K类问题构造K个两类分类器).该方法存在分类重叠以及不可分类的缺点.与一对一以及一对多方法对比，多层次SVM分类方法的复杂度更低，能够快速完成分类.多层次SVM分类算法的框图如图2所示.首先，对RCMSE进行特征提取，然后，根据RCMSE曲线的分布特征来确定不同层次的输入参数.分类器由3层组成：第1层将信号分为睡眠期以及清醒期，第2层以及第3层分别在上一层分类结果的基础上进行更深层次的分类，直到将睡眠阶段分为5个独立的时期.其中，RCMSE 值为输入特征，随机选取其中的部分数据进行分类器训练，剩下的睡眠数据用于分类器的预测.通过对比预测的睡眠分期结果与人工判读的睡眠分期标签，获得睡眠自动分期的准确率.

2 结果与分析

2.1 RCMSE分析

EEG信号是睡眠分期准则的主要判别标准，所以本文首先选取EEG信号，参考导联为Fpz-Cz通道，所得EEG信号的RCMSE的变化曲线如图3所示.其中，不同的点表示各个时期的RCMSE均值，其上下竖线表示RCMSE标准差.根据RCMSE的变化趋势确定分类器的层数以及设置每一层次的输入参数.由图3可见：W期与其他时期EEG信号的RCMSE的差别较为明显，所以在分类器的第1层将数据分为清醒期和睡眠期；N1期、R期与N2期、N3期的RCMSE的区分度较高，在第2层SVM中对其进行分类；N2期与N3期的RCMSE的差异明显，可在第3层分类器中对其分类.

图3 脑电信号EEG通道的RCMSE变化曲线Fig.3 RCMSE curves of channel EEG

参考AASM睡眠及相关事件判读手册[14]，可以发现睡眠R期的低波幅混合频率与N1期的相似，2个时期的EEG信号相似度较高，但其EOG信号存在差异.其中，N1期为缓慢眼动，而R期出现了快速眼动的现象.相应地，由图3可见，N1期与R期EEG信号的RCMSE变化趋势非常相似，且其区分度较差，通过EEG信号的RCMSE变化特征难以区分这2个时期.为此，本文提取研究对象的EOG信号进行N1期以及R期的分类.图4所示为EOG信号的RCMSE变化曲线.可见，N1期与R期的区分效果得到了改善.

图4 眼电信号EOG通道的RCMSE变化曲线Fig.4 RCMSE curves of channel EOG

人工的睡眠分期准则对于特征的选择具有重要的参考价值.这个睡眠分期准则充分结合信号的整体与局部信息，根据不同的规则判别睡眠时期.具体方法：① 在判读N1期时，1帧图像中整体背景特征满足低波幅混合频率(3～7 Hz)的成分所占比例超过50%，即低波幅混合频率波的宽度所占比例超过50%，该准则表征了信号的整体特点；② 在判读N2期时，需要运用局部短时的K-复合波特征，该准则表征了信号的局部特点.与人工的睡眠分期准则对应，本文提出的基于RCMSE特征的睡眠分期方法能够通过特征尺度的变化来表征信号的整体或局部特点：当特征尺度τ=1时，能够表征信号的整体特征；当τ不断增大时，能够表征信号的局部特征.通过比较RCMSE的均值以及标准差，优先区分差异性较大的睡眠时期，因此，将RCMSE作为信号的特征输入能够较好地反映睡眠信号的复杂度.

分析上述RCMSE的变化曲线可以看出，N1期与R期的区分度较低，N2期与N3期的变化趋势相似.其中，N2期与N3期在τ处于1～10范围内的区分度较高.因此，选择容易区分的尺度范围作为多层次SVM分类算法的特征输入，可以保证分类效果并且提高工作效率.对于每层的分类节点，选取的 RCMSE 特征尺度以及对应的通道见表1.

表1多层次SVM分类的通道以及特征提取

Tab.1RCMSEfeaturesandchannelforSVMclassificationmethod

分类器τ通道清醒期与睡眠期1～20EEG(Fpz-Cz)N1期和R期与N2期和N3期1～20EEG(Fpz-Cz)N1期与R期1～20EOGN2期与N3期1～10EEG(Fpz-Cz)

2.2 睡眠分期结果

表2列出了睡眠的SVM自动分期结果与人工判读分期结果的对比.表中，对角线上的黑体数值为准确判读的数据量，非对角线的数值为误判数据.根据表2中的内容，采用本文算法计算所得各个独立睡眠时期的分类准确率如表3所示.由表3可见：清醒期的分类在第1层SVM分类器中完成，其分类准确率最高，达到了 92.4%；第3层SVM分类器完成对N1期的分类，由于N1期与R期的特征最相似，其中N1期的部分数据被人工误判为R期，同时，在整个睡眠阶段的N1期数据较少，所以最终导致N1期的人工判读准确率较低；N2期及N3期的分类准确率分别达到了 89.2% 以及 90.0%.SVM分类器每一层次的分类效果都会对最终的分类结果产生影响，其中W期、N2期、N3期、R期的分类准确率均高达85%以上，从而保证了各个睡眠阶段的分类效果.

表2 SVM分类和人工判读结果Tab.2 The classification results of SVM

表3 独立睡眠时期的准确率Tab.3 Accuracy for individual stages

2.3 睡眠分期方法比较

将本文算法与文献[15-17]中的算法进行比较，所得到的分类准确率如表4所示.由表4可见，与文献[15-17]中的算法相比，本文所提出的算法的分类准确率有所提高.另外，由表5可见，本文算法在W期、N1期、N2期以及N3期的分类效果均比文献[18]中的算法更优，同时，在R期也保持了较高的分类准确率.针对文献[19]中的算法不能准确区分睡眠R期的问题，本文算法有所改进，在该阶段的分类准确率有所提高，并且在其他阶段也保持了较高的分类准确率.通过对比各个独立时期的分类结果可见，本文算法具有更加平衡的输出，并且总体的分类准确率更高.因此，相对其他的算法，本文提出的算法具有较好的稳定性.

表4 不同算法的分类准确率比较Tab.4 Comparison of classification accuracy

表5 独立时期的分类准确率比较Tab.5 Performance comparison of individual stages

3 结语

本文提出了基于RCMSE特征的多层次SVM睡眠自动分期模型.从研究对象的EEG信号以及EOG信号中提取RCMSE特征，以RCMSE值作为研究的唯一特征，它可以从多个尺度表征生理信号的复杂度，对于较短的数据可得稳定的RCMSE值，其抗噪能力强，为睡眠分期提供了良好的输入参数来源.总体的分类器框架基于多层次SVM分类展开，根据RCMSE的变化曲线对分类器层次进行设置，所得睡眠分期的准确率达到了 85.3%，从而验证了所提算法对睡眠分期的可行性和有效性.

然而，在本文的研究中，仅选用EEG信号以及EOG信号作为评价标准，其分类准确率有待于进一步提高.研究表明，在不同的睡眠状态下，周期性的腿动信号与翻身信号有明显的差异.其中，腿动信号的相对频率、持续时间和引起醒觉的效应都随着睡眠的加深而逐渐下降，而腿动间隔时间将随之增加，这对于判别睡眠阶段有所帮助.因此，下一步将研究受试者的体动信号，以获取体动能量值，并利用多信息融合技术分析受试者的睡眠阶段.