一种具有鲁棒性的无证书部分盲签名

曾丽，李旭东

（西华大学理学院，成都610039）

0 引言

部分盲签名的定义首次被Abe和Fujisaki[1]在1996年提出，次年，Abe等人[2]中又给出了具体的基于RSA和Schnorr算法的部分盲签名方案。部分盲签名不仅是盲签名的进一步发展，更是很好地解决了盲签名存在的问题。与盲签名的不同之处在于，它可以填加一些双方已经协商好的信息，如签名周期、签名时间等。这样即保证了代签消息的部分盲性，也保证了签名者的合法权益。

2008年，荣维坚[3]结合无证书密码体制，第一次提出无证书的部分盲签名方案，但未证明该方案的不可伪造性。2010年，余丹等人[4]荣方案的存在的问题，提出了改进的部分盲签名方案。在此期间，一些基于不同算法的无证书部分盲签名的方案相继被提出[5-9]，这部分方案中，大多是都采用了双线性对，这种运算计算开销大。2012年，邵国金等人[10]提出一种基于椭圆曲线DLP的无证书部分盲签名方案，该方案大大降低了签名和签名验证过程中的计算开销。2016年，赵振国[11]针对文献[10]所提出的方案不能提供不可伪造性这一问题，提出了新的无证书部分盲签名方案。

本文对文献[11]通过公共信息被篡改具体的攻击，指出该方案存在安全问题：恶意用户可以在毫不被察觉的情况下，更改公共信息（双方事先协商好的部分），让签名者的权益受到威胁，失去对消息的可控性。本文针对这个问题，提出了一个改进的方案，改进的方案不仅能够抵抗公共信息被篡改，在满足部分盲性、不可伪造性等安全性需求的同时，计算效率还得到了进一步提高。

1 预备知识

（1）椭圆曲线的离散对数问题

给定定义于有限域Fq上的椭圆曲线E，选择一个点P∈E(Fq)作为基点，P的阶数为素数n，Q∈P，对于任意的a∈，给定P，由Q=aP计算a。整数a称为Q的基于P的离散对数，表示为a=。

（2）计算Diffie-Hellman问题

2 方案的回顾

2.1 方案的回顾

文献[11]中的无证书部分盲签名方案由以下四个协议构成：

（1）设置

设 p、q是两个大素数，G是由E(Fp)是椭圆曲线上的点组成的阶为q加法群；

P0=sP为KGC的公钥，其中，s∈是KGC的主密钥，P是G是的一个基点。H1、H2、H3是安全的单向散列函数，H1：{0 ,1}∗×G→，H2：{0 ,1}∗×{0 ,1}∗×G→，H3：{0 ,1}∗×{0 ,1}∗×G×G×G→。 系统公布参数{p,q,E(Fp),G,P0,H1,H2,H3}。

（2）密钥设置

签名者B将其身份IDB发送给KGC，KGC随机选择 yB∈，计 算YB=yBP ，qB=H1(IDB,YB)和dB=yB+sqB，KGC 返回dB、YB，dB、YB分别作为 B的部分私钥、部分公钥。B选择任意的xB∈作为其私有秘密，计算XB=xBP，并且输出B的私钥SB=(xB,dB)和公钥PB=(YB,XB)。

（3）签名协议

用户A请求签名者B对消息m签名，c是双方共同协商的公共信息，签名过程如下：

Step3.签名（阶段2）：签名者B计算k=H3(c,IDB,XB,YB,P0)，v=r-u(kxB+dB)，将v返回给A；

Step4.去盲：A收到 v后，计算 w=βv+α，则(h,w)是(m,c)的部分盲签名。

（4）签名验证

验证者通过计算qB=H1(IDB,YB)，k=H3(c,IDB,XB,YB,P0)和T=h(kXB+YB+qBP0)+wP来验证等式h=H2(m,c,T)是否成立。如果等式成立，则接受签名，反之亦然。

2.2 方案的分析

通过分析，文献[11]方案存在公共信息被恶意篡改的问题。假设攻击者将公共信息c修改为c1（c≠c1），利用自己伪造的c1执行签名过程，如下：

用户A请求签名者B对消息m签名，c1是双方共同协商的公共信息，签名过程如下：

Step3.签名（阶段2）：签名者B计算k∗=H3(c1,IDB,XB,YB,P0)，w∗=r-u∗(k∗xB+dB)，将 v∗返回给A；

Step4.去盲：A收到 v∗后，计算 w∗=βv∗+α，输出对(m,c1)的部分盲签名 (h∗,w∗)

验证过程：

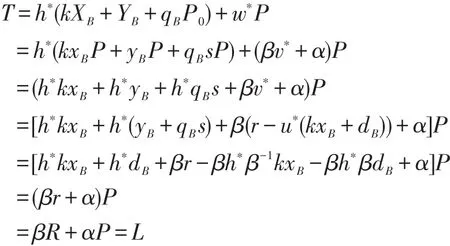
因此，验证者也可以验证(m,c1)的部分盲签名(h∗,w∗)是有效合法的，在不被察觉的情况下，恶意的用户就将协商好的公共信息进行了篡改。

3 新的无证书部分盲签名方案

针对文献[11]中存在的问题——任意篡改公共信息，本文在原方案的基础上进行了改进，改进方案的密钥产生算法与文献[11]相同，在设置中增加了安全的散列函数H4。密钥设置、签名协议和签名验证如下。

3.1 设置

设 p、q是两个大素数，G是由E(Fp)是椭圆曲线上的点组成的阶为q加法群；

P0=sP为KGC的公钥，其中，s∈是KGC的主密钥，P是G是的一个基点。H1～H4是安全的散列函数 ， H1：{0 ,1}∗×G→， H2：{0 ,1}∗×{0 ,1}∗×G→，H3：{0 ,1}∗×{0 ,1}∗×G×G×G→，H4：E(Fp)→。系统公布参数{p,q,E(Fp),G,P0,H1,H2,H3,H4}。

3.2 密钥设置

签名者B将其身份IDB发送给KGC，KGC随机选择yB∈，计 算YB=yBP ，qB=H1(IDB,YB)和dB=yB+sqB，KGC返回dB、YB，dB作为B的部分私钥，YB作为B的部分公钥。B随机选择xB∈Zq*作为其私有秘密，计算XB=xBP，并且输出B的私钥SB=(xB,dB)和公钥PB=(YB,XB)。

3.3 签名协议

用户A请求B对消息m签名，c是双方共同协商的公共信息，签名过程如下：

Step3.签名（阶段2）：签名者B计算k=H3(c,IDB,XB,YB,P0)，v=rz-u(kxB+dB)，将v返回给A；

Step4.去盲：用户收到 v后，计算w=βv+α，输出对(m,c)的部分盲签名(h,w)。

3.4 签名验证

验证者计算qB=H1(IDB,YB)，k=H3(c,IDB,XB,YB,P0)和 z=H4(c)，验证等式wP+h(kBXB+YB+qBP0)=L是否相等。若相等，则接受签名，否则拒绝。

4 新方案分析

4.1 正确性

新方案的正确性证明如下：

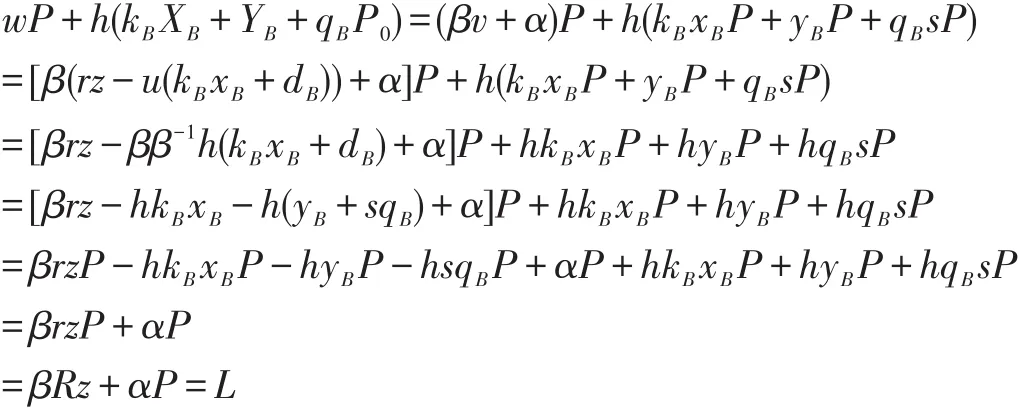
4.2 部分盲性

针对本文使用的两个盲化因子α,β∈Zq*，如果签名者私自保留了u，由于H2是一个安全的哈希函数，签名者不能从h=H2(m,c,L)中恢复出信息m。考虑到以下三个式子：

一定存在唯一的 β=hu-1使式（2）成立。如果任意一个签名(h,w)是有效的，可以计算出唯一的α=w-hu-1v，使得 wP+h(kBXB+YB+qBP0)=L=αP+zβR成立。因此，盲因子α,β一直存在于在部分盲签名中。根据文献[11]中定义1，由于α,β一直存在，所以攻击者赢得游戏的优势可以忽略。因此，改进的方案能够满足部分盲性。

4.3 不可伪造性

一般情况下，签名者的私钥只有自己知道，假设攻击者AI通过访问获取了系统的三个参数(s,dB,PB)，但是他不知道xB。攻击者 AI如果想从XB=xBP获取xB，则他需要解决DLP困难问题。因此不可能获取SB，无法伪造出有效签名。

假设攻击者将公共信息c修改为c1（c≠c1），攻击者利用自己伪造的公共信息c1执行改进方案的签名协议。由于协商的公共信息和签名人的私钥绑定在一起，如果想篡改c，那么他需要解决CDHP困难问题，显然也是不可性的，所以改进后的方案能够抵挡攻击者恶意篡改公共信息c。

4.4 效率分析

改进的方案与文献[10-11]中的方案进行比较，求解时作出以下假设：p为1024比特；q为160比特；n为1024比特；安全单向哈希函数的输出大小为160比特；H、M和E分别表示哈希函数计算时间、椭圆曲线点加的计算时间和点乘的计算时间。在计算机仿真实验中，操作系统采用Windows 7系统，CPU主频率为3.40GHz，内存为4GB。通过编程实现了椭圆曲线密码所需要的各种运算，其中：H≈0.0001ms，E≈0.442ms，M≈0.0018ms。结果见表1。由于多次使用哈希生成值来代替椭圆曲线上的点乘运算，所以计算性能优于文献[10]和文献[11]。

表1 改进后的方案与其他方案的计算效率比较

5 结语

本文对赵振国提出的可证安全的无证书部分盲签名机制进行了分析，发现该方案并不安全，不能够承受公共信息被篡改的攻击，本文为了解决这个问题，在文献[11]的基础上，提了一个改进的方案，通过分析表明，新提出的方案是正确的，满足不可伪造性和部分盲性，方案的总体安全级别高于同类方案，并且在效率上比邵的方案和赵的方案更具有优势，具有广泛的应用。