结冰条件下的飞行控制律重构设计方法

王良禹， 徐浩军， 李颖晖， 李哲

(空军工程大学航空工程学院， 西安 710038)

近年来，由飞机结冰而引发的飞行事故时有发生，造成了大量的人员伤亡和财产损失。飞机结冰是指在飞行过程中遭遇结冰天气而机体表面产生结冰的现象，是影响飞行安全的重要因素之一。针对飞机结冰问题，国内外都开展了大量的研究工作[1-4],飞机的防/除冰系统也由此得到迅猛发展[5-7]，但是仅依靠防除冰系统也无法保证不会出现残留冰或者由结冰引起的飞行事故不会发生，例如2006年某型飞机就因为飞机结冰而导致失控坠毁。因此，开展对飞机结冰后的飞行安全保障方法研究很有必要。研究结冰对飞机飞行性能和飞行品质的影响、结冰条件下的飞行控制律重构设计以及结冰后边界保护等是保障飞机安全飞行的重要手段[8-11]。

目前，关于飞机飞行控制的理论与方法有很多。美国Bragg教授等开发了飞机智能结冰系统(Smart Icing System,SIS)[12]，为飞机容冰飞行控制和结冰边界保护提供了思路。Aykan等通过神经网络、容错控制等方法开展了飞机结冰后控制律重构的研究工作[13-14]。国内相对起步较晚，对结冰后的飞行控制律重构和边界保护等研究还比较薄弱。北京航空航天大学的杜亮和洪冠新[15]研究了结冰对飞机飞行包线的影响。空军工程大学的王小龙等[16]引入铰链力矩检测模块，研究了基于飞机自驾仪的结冰后边界保护方法。复旦大学的应思斌[17]开展了对容冰控制理论与方法的研究，建立了综合结冰保护系统。然而，从目前的公开文献来看，对结冰后飞行控制律重构设计及边界保护方法的系统研究还不足，成果也相对较少。

飞机的动态模型具有很强的非线性特征，而传统的基于小扰动线性化的控制方法已越来越不能满足任务需求，这就要求一种能满足非线性系统的控制方法。反馈线性化理论在近年来得到迅猛发展[18-19]，对非线性系统具有很好的控制效果。但是由于其需要依赖精确的系统模型，易受模型中的不确定性因素及外界环境的影响，抗干扰性较差。

Bragg教授等提出一种线性的结冰影响模型，受到了广泛应用[1]。然而该模型对大迎角及过失速阶段的描述并不准确，因此，本文在前人的基础上建立了非线性结冰影响模型，并构建了结冰飞机纵向非线性动力学模型。通过将反馈线性化理论与模糊控制原理相结合，设计了飞机结冰情形下的飞行控制律。一方面通过反馈线性化保证了飞机纵向运动的动态特性，另一方面利用模糊控制原理较强的鲁棒性，改善了反馈线性化对模型精度的依赖及其抗干扰能力。在不同结冰严重程度以及干扰下进行仿真计算，并与传统PID控制进行对比，验证了本文所设计控制律的有效性，具有较强的理论意义和工程应用价值。

1 结冰后飞机非线性动力学模型

1.1 结冰影响模型

现有的公开文献中，Bragg等[1]提出了一种线性的结冰影响模型，并得到了广泛的应用：

C(A)iced=(1+ηKC(A))C(A)

(1)

式中:C(A)和C(A)iced分别为飞机结冰前后的气动参数；η为结冰因子，仅与气象条件有关，反映不同结冰严重程度，其值越大表明结冰越严重，一般取值范围大致为0～0.3；KC(A)为结冰系数，仅与飞机有关，对于给定飞机时为常值。然而，该模型对大迎角及过失速阶段的结冰后气动特性的描述并不准确，且未能体现失速迎角的变化，仅适合于失速前的线性阶段。

图1为NACA 0012翼型的升力系数CL曲线[20]，从图中可以看出，在失速前飞机的升力系 数减小，升力线斜率降低，并呈现线性变化；而在过失速阶段，随着结冰严重程度的增加，升力系数曲线变得平滑，且大于失速迎角时的升力突变现象也变得不再明显。这是因为结冰主要是通过改变流场而产生影响，而在过失速阶段，由于迎角α较大气流早已产生分离，飞机上的积冰对流场的影响也变得不再明显。

图1 NACA 0012翼型升力系数曲线[20]Fig.1 Lift coefficient curves of NACA 0012 airfoil[20]

因此，在线性结冰影响模型的基础上，通过改变KC(A)值，使其随着迎角的变化而改变，构建了非线性结冰影响模型，以完善结冰对气动特性影响的描述。KC(A)的变化情况如下：

1) 在接近失速迎角αstall前，KC(A)的取值与线性结冰影响模型一致。通过仿真得到不同结冰程度下的失速迎角，再利用插值则可得到对应η值下的失速迎角αstall。

2) 进入失速区后，通过拟合得到KC(A)的值，使结冰后的气动参数趋近于未结冰时的值。

3) 当迎角增大到某一阀值α1时，KC(A)应取值为0。

以Z轴上的气动力系数CZ对升降舵偏角δe的导数CZδe为例，对应的KC(A)值如下：

(2)

式中：a1等为关于η的多项式函数，可通过拟合得到，限于篇幅原因不做详细叙述。通过仿真得到基于非线性结冰影响模型的升力系数曲线，如图2所示。

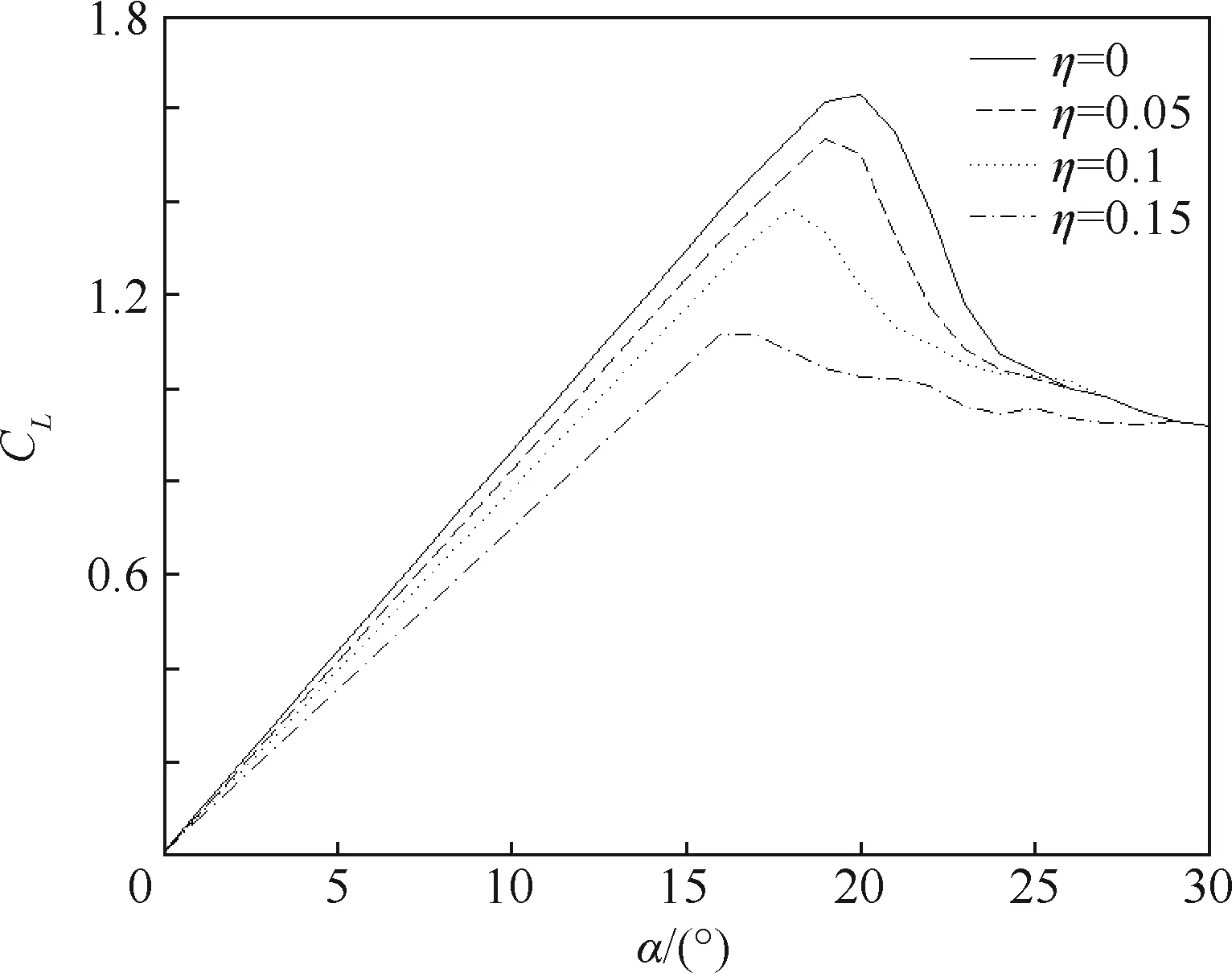
图2 升力系数曲线Fig.2 Lift coefficient curves

1.2 飞机纵向非线性动力学模型

飞机结冰后，飞行包线萎缩，而飞机的俯仰运动会对飞机的飞行安全产生直接的影响。因此，飞机的纵向俯仰运动是本文研究的重点，其简化的动力学模型可表示为

(3)

(4)

式中:V、θ和q分别为飞机的速度、俯仰角和俯仰角速度；S和b分别为机翼面积和平均气动弦长；m和Iy分别为飞机质量和惯性矩；δp为发动机转速百分比；T、D、L和M分别表示发动机推力、阻力、升力和俯仰力矩，且T=f(δp)；g为重力加速度；CD和Cm分别为阻力系数和俯仰力矩系数；ρ为空气密度；x为状态向量，这里取x=[V,α,θ,q]T。

飞机的纵向非线性气动力模型为[21]

(5)

式中：CX为机体X轴上的气动力系数，通过插值计算得到。通过坐标转换，可得到飞机的升力系数CL和阻力系数CD：

(6)

引入结冰影响模型，即可得到结冰后的非线性气动力模型。以CZ为例，则结冰后的非线性气动力系数可表示为：

CZiced=(CZ(α)-CZ0)(1 +KCZαη)+

CZ0(1 +KCZ0η)+CZ(α,δe)(1+

KCZδeη)+CZ(α,q)(1+KCZqη)

(7)

式中：CZiced为结冰后的CZ值;CZ0为迎角α=0°时的CZ值；KCZα、KCZq和KCZ0分别为气动导数CZα、CZq和气动参数CZ0对应的KC(A)值。

2 结冰后的纵向飞行控制律设计

随着航空工业的快速发展，飞机的非线性问题也受到越来越多的关注，而基于小扰动线性化的控制方法愈来愈不能满足发展的需求。本节基于所建立的结冰飞机纵向非线性动力学模型，将反馈线性化理论与模糊控制原理相结合，重构设计了结冰情形下的飞行控制律，保障了飞机在结冰条件下具有一定的飞行能力。

2.1 纵向飞行品质要求

在飞机纵向运动过程中，对于长周期响应而言飞行员一般有足够的时间进行操和修正，而往往却因为短周期响应较快导致飞行员来不及进行操纵和修正，容易引发飞行事故。因此，绝大多数纵向飞行品质要求是针对短周期建立的。依据文献[22]，给出了飞机纵向飞行品质要求，如表1所示。

表1 纵向飞行品质要求Table 1 Longitudinal flight quality requirements

2.2 纵向飞行控制律设计

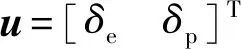
(8)

可得：系统的相对阶r=r1+r2=3<4。对原系统进行如下变化：

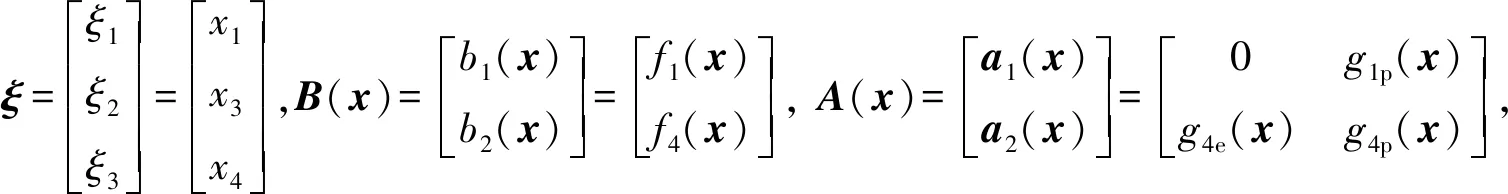
(9)

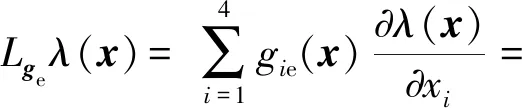
(10)

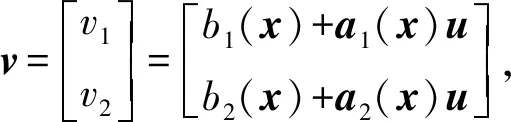
(11)

构造模糊控制器，将其输出作为反馈线性化的等效输入v，即可实现反馈线性化理论与模糊控制原理的结合，完成纵向控制器的设计。下面给出模糊控制方法，图3为模糊控制器的结构原理图。

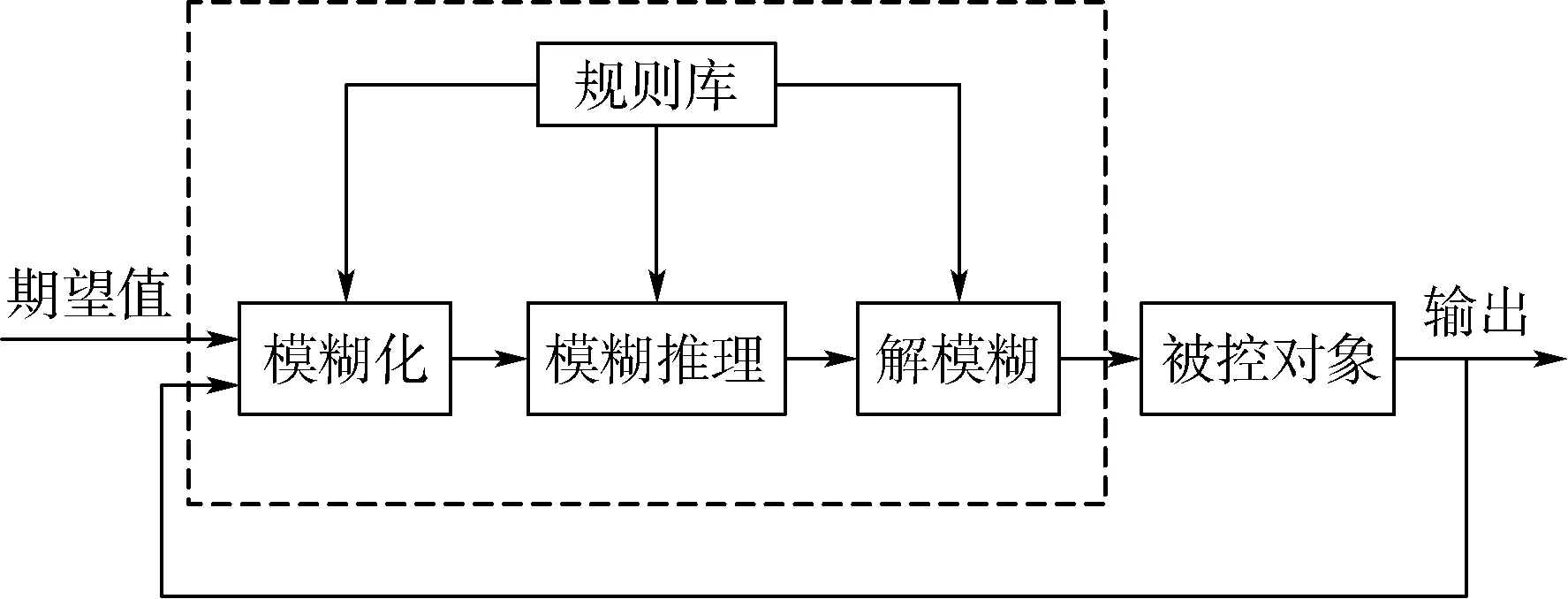
图3 模糊控制原理图Fig.3 Schematic diagram of fuzzy control

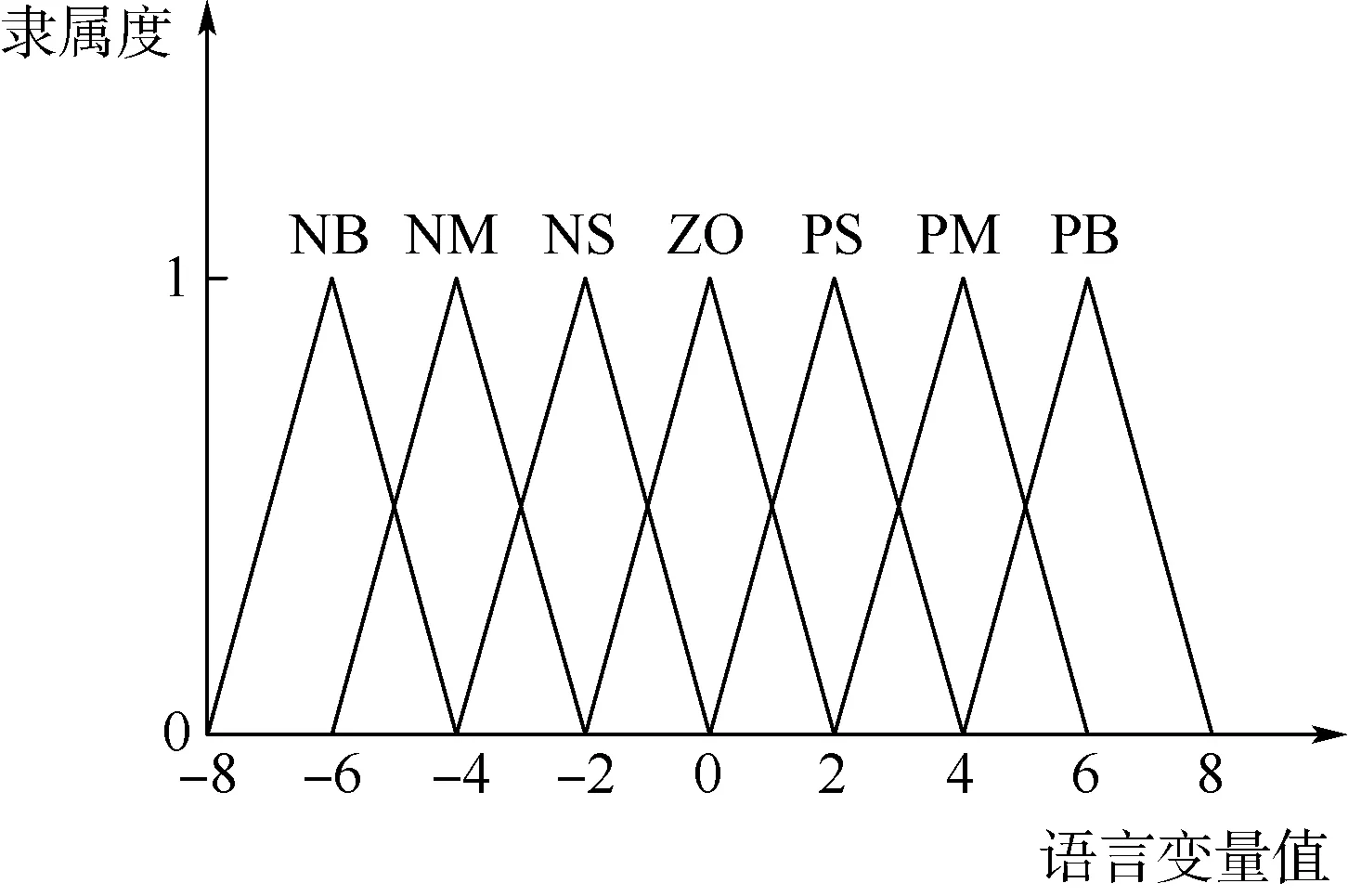
图4 隶属函数的形状及分布Fig.4 Shape and distribution of membership functions

建立相应的模糊语言规则库，如表2所示。

基于MATLAB/Simulink建立模糊控制系统，与反馈线性化控制器相结合，即可完成飞机纵向控制律的设计。图5为模糊控制系统的Simulink仿真结构,θ和θd分别为俯仰角和俯仰角指令，图6为飞机纵向控制律的模块结构。

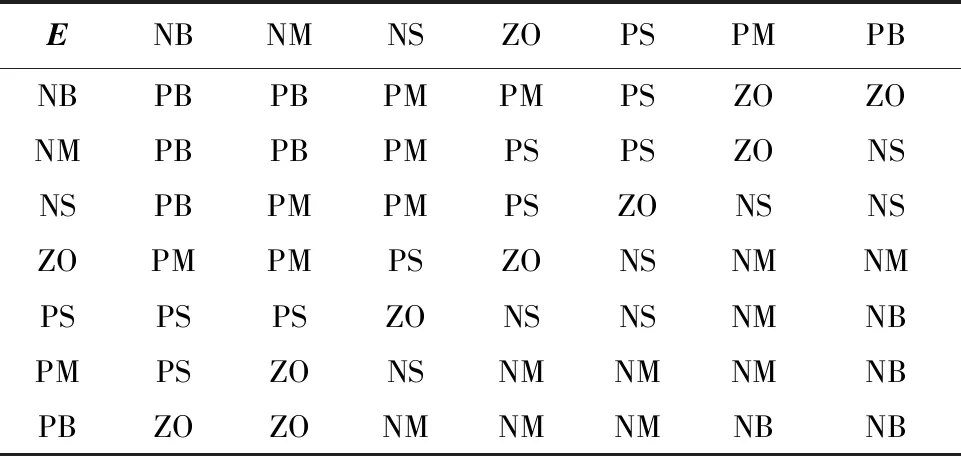
表2 模糊语言规则库Table 2 Fuzzy language rule base

图5 模糊控制系统的Simulink仿真结构Fig.5 Simulink simulation structure of fuzzy control system

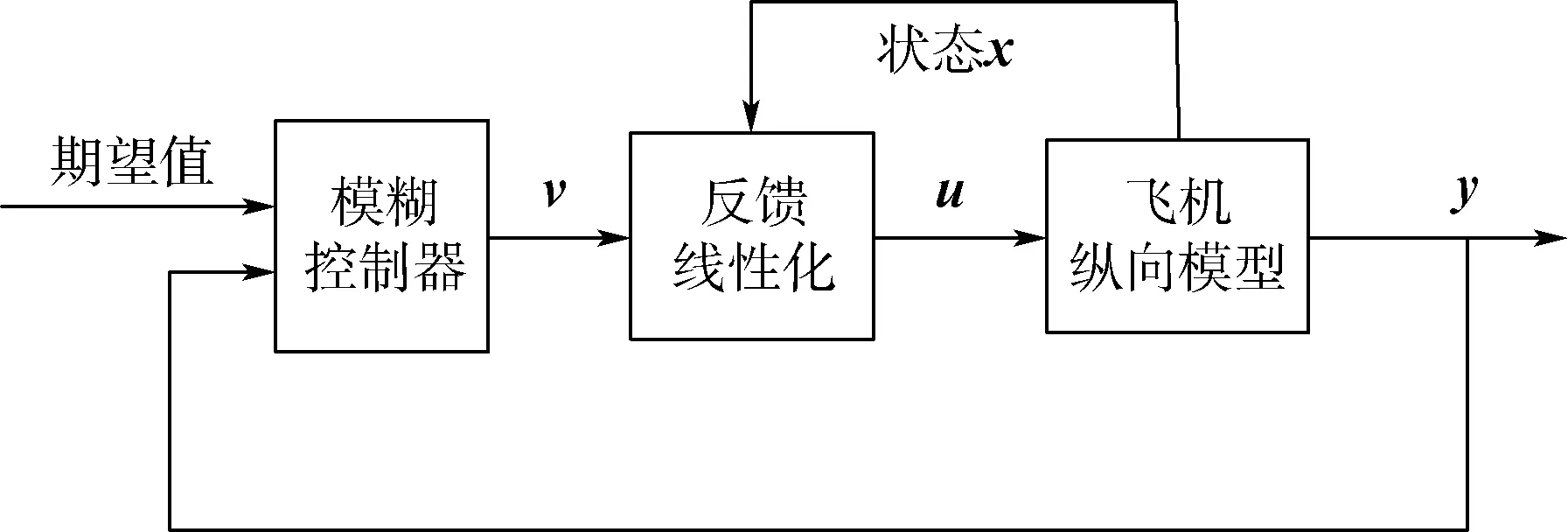
图6 纵向控制系统的结构模块Fig.6 Structural module of longitudinal control system

3 仿真验证分析

以某型飞机为例，初始条件设为：高度H=3 km、速度V=140 m/s，基于本文所建立的动力学模型及飞行控制律方案进行仿真验证，分析结冰对飞机动态响应特性的影响及该控制律设计方案下飞机在不同结冰严重程度和干扰下的动态响应特性，并与常规PID控制进行比较，其中PID控制器的各参数为kP=-5.694、kI=-4.238、kD=-6.612。

3.1 结冰后的动态响应特性分析

保持飞机初始状态为平飞状态，假设结冰因子η从0线性增加到0.3，来模拟从干净外形到轻度结冰再到严重结冰。在无指令修正情况下，对不同结冰严重程度下飞机的纵向动态响应特性进行仿真分析，图7为飞机的纵向动态响应曲线。

从图7中可以看出，飞机结冰后，其纵向动态响应出现了振荡现象，且在无指令修正情况下飞机逐渐偏离了平衡状态。随着结冰严重程度的增加，纵向响应振幅增大、衰减变慢，而迎角增大使得飞机面临有可能失速的危险，严重威胁飞行安全。因此，有必要采取适当的控制方法，来保障飞机在结冰条件下的飞行安全。

3.2 基于纵向飞行控制律的仿真验证分析

保持初始状态不变，仿真时给定俯仰角指令θd=8°和速度指令Vd=140 m/s，并引入零均值随机白噪声信号来模拟干扰因素。针对本文所设计的纵向控制律，设定飞机遭遇不同严重程度的结冰，并给定中等程度的干扰进行仿真分析。表3为设计控制律和PID控制作用下俯仰角响应的性能品质，图8为在2 种控制方式作用下的动态响应曲线。

从表3中可以看出，在设计控制律作用下的俯仰角响应较快，稳态误差和超调量均为0，而随着飞机结冰严重程度的增加，其上升时间和调节时间均有增加，但仍满足性能品质要求。相比较而言，设计控制律下的时域品质明显优于常规PID控制器下的性能品质，在结冰因子η=0.3时，其上升时间也只有0.51 s，调节时间仅有0.92 s。

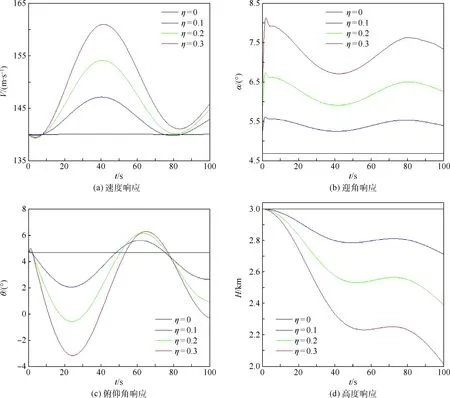
图7 结冰飞机动态响应曲线Fig.7 Dynamic response curves of icing aircraft

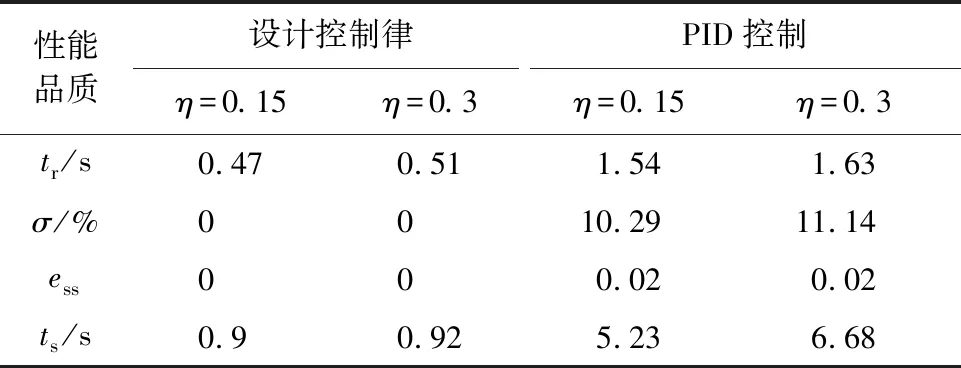
性能品质设计控制律PID控制η=0.15η=0.3η=0.15η=0.3tr/s0.470.511.541.63σ/%0010.2911.14ess000.020.02ts/s0.90.925.236.68

从图8中可以看出，在2种控制方式下，速度响应变化趋势基本一致。比之于PID控制，在设计控制律下的俯仰角响应能以更快的速度收敛到稳定值，并且受其他干扰因素的影响不大。随着飞机遭遇结冰及结冰严重程度的增加，飞机的迎角增大，容易触发失速迎角，而相比于常规PID控制器，设计控制律作用下的迎角响应幅值更小、衰 减更快。对比俯仰角速度曲线，设计方案下的俯仰角速度幅值较大、衰减更快，才使得俯仰角能快速地收敛到稳定值。

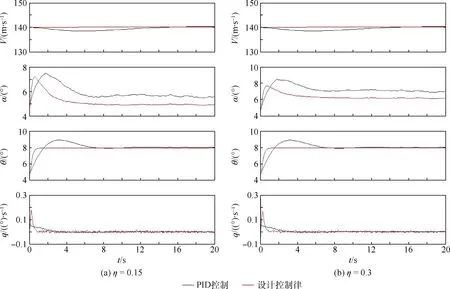
图8 中等程度干扰下结冰飞机纵向响应曲线Fig.8 Longitudinal response curves of icing aircraft under moderate interference

4 结 论

1) 基于线性结冰影响模型，建立的非线性结冰影响模型能更为准确地描述在大迎角及过失速阶段结冰对飞机的影响，且体现了失速迎角的变化情况。

2) 本文所设计的飞行控制律方案，比常规PID控制器具有更优的时域性能品质，其俯仰角响应的超调量和稳态误差均为0，相比较而言上升时间快1 s左右，调节时间快5 s左右。

3) 将反馈线性化理论与模糊控制原理相结合，既改善了控制方案的抗干扰能力，也保证了较强的动态响应特性，具有较强的理论价值和应用价值。