基于近似动态规划的目标追踪控制算法
2019-04-08李惠峰易文峰程晓明
李惠峰, 易文峰, 程晓明,2
(1. 北京航空航天大学宇航学院, 北京 100083; 2. 北京航天自动控制研究所, 北京 100854)
无人机具有结构简单、成本低廉等优点,是用于自主追随的理想平台。近年来,随着自动化技术、计算机技术、电子器件等高新科技水平的不断提高,无人机在民用领域也大有可为,它可应用于:跟踪拍摄、无人机集合作战等领域,市场前景非常乐观,具有巨大的经济意义,而这些功能的实现都依赖于无人机对目标的精确跟随。
目前国内实现无人机自主跟踪主要通过低空飞行的无人机搭载无线相机,通过相机视觉传达无人机与目标的水平位移,进而通过控制装置调节无人机的位置以及姿态,使得无人机紧随跟踪目标。但是因为整个跟踪过程基于视觉系统,所以存在背景运动、噪声、目标被遮挡以及目标逃出视野之外的等等问题,且其算法还需利用实时图像计算其跟踪对象的像素点变化从再计算得出机动规律,使得无人机自主飞行控制的变得低效以及不准确。另外如果得到较好的目标位置,其控制部分往往研究比较少,只是简单地使用控制器跟随当前目标位置,无法预测目标的下一个可能位置,加上如果应用背景是无人机博弈等对策问题,预测目标的位置显得十分重要。目前利用图像获得相对位置的方法已经较为成熟[1],如在线目标跟踪算法中的均值偏移算法[2]、子块跟踪算法[3]、子空间算法[4],滤波算法中的特征改进、多核算法[5]、尺度估计[6-8]、分块算法[9]等,深度学习中的深度目标跟踪算法[10]等,可以解决大多数图像跟踪存在的问题,但其控制器的目标都几乎只是计算目标与无人机的距离而设计控制器,之后将目标放在图像中心[9],而忽视了从控制方面改善跟踪效果。如果在控制方面加上对目标的预测,那么跟踪效果也会得到很大的改善且也可以将之使用于博弈控制,改善了现有控制算法不灵敏,对图像依赖大的问题。
本文将近似动态规划的方法应用于无人机自主追随的问题,如果已知目标的位置等条件,使用提前使用博弈方式训练好无人机的特征参数的方法,那么本文算法可以使无人机做出更好更快的选择。最后,对设计的算法进行了仿真实验,验证了算法的可行性及其良好的跟踪性能。
1 近似动态规划
基于贝尔曼方程的动态规划为无人机跟随的最佳机动策略提供了新的手段,由此产生的优化策略为无人机跟踪问题提供了更好的方法,即在给定的飞行状态下,对最优跟踪控制策略的求解,不需要大量的在线计算,能够完成实时的最优跟踪。尽管动态规划方法非常适合应用于这类问题,但是其不适用于求解计算量较大的问题,因为离散状态空间大小随状态空间变量的数量成指数增长,从而产生维数灾使得算法难以实现。而基于动态规划的近似动态规划(Approximate Dynamic Programming, ADP)为解决复杂且庞大的最优跟踪控制问题提供了新的可能。
近似动态规划使用的基本原理是利用函数近似结构(比如神经网络),来逼近经典动态规划中的性能指标函数,从而逼近得到最优性能指标和最优控制,近似动态规划的结构如图1所示[11]。
近似动态规划算法主要由3部分组成:动态系统、执行网络和评价网络。在实际应用中,每个部分的实现由神经网络执行。当系统模型未知时,可以通过神经网络对系统模型进行辨识;执行网络生成系统的控制策略,通过调节执行网络的参数来达到逼近最优控制策略的目的;评价网络用于评价执行网络生成的控制策略。不同于传统的反馈控制方法,图1中评价网络到执行网络的增强信号是对执行网络控制策略的评价结果,这一信号有助于指导执行网络的优化设计。本文需要指出执行网络和评价网络的权值调整优化目标之间的区别:评价网络的参数优化的目标函数是使得评价网络的输出满足贝尔曼方程;建立在评价网络基础上,执行网络参数优化的目标是最小化评价网络的输出。
J(xk)=r(xk,uk)+J(xk+1)
(1)
式中:r(xk,uk)通常被称之为回报函数(reward function);在k时刻,以J(xk)性能指标表示为状态xk的函数;在k+1时刻,性能指标则可以表示为J(xk+1)。根据贝尔曼最优性原理[12]
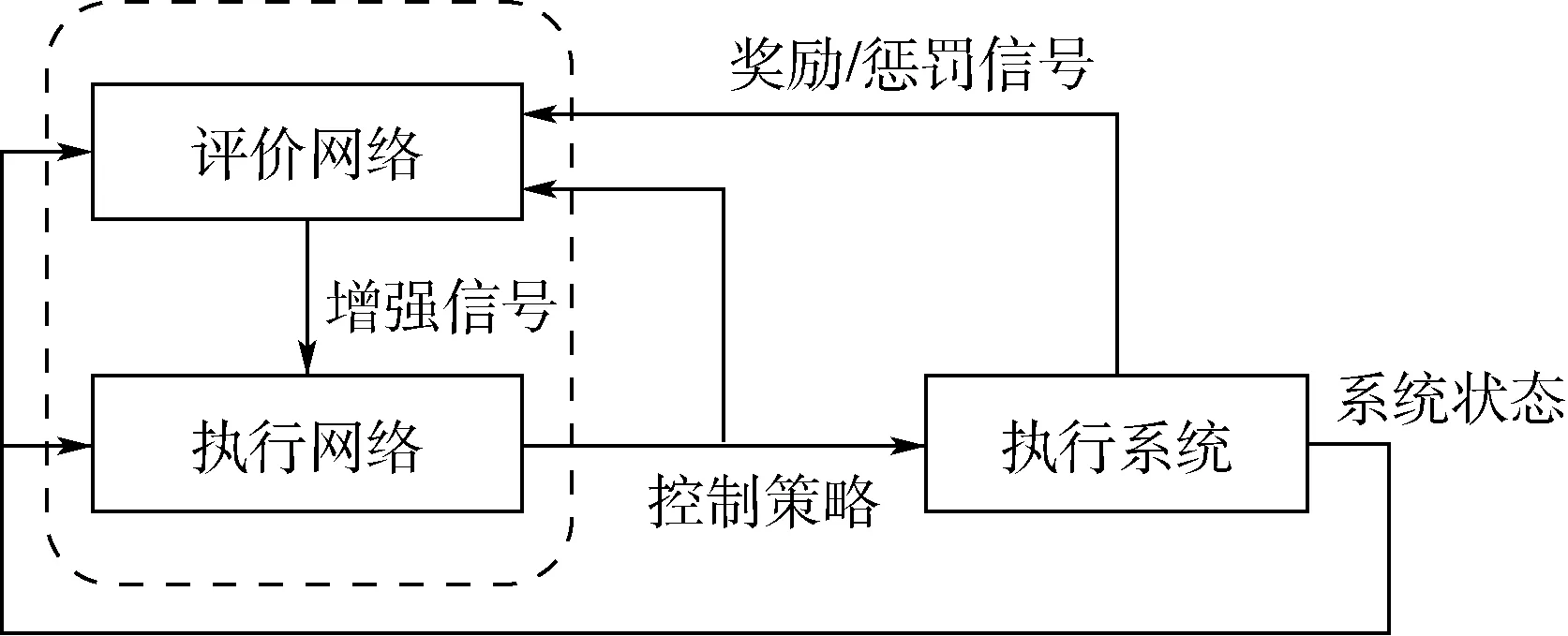
图1 近似动态规划结构[11]Fig.1 ADP structure[11]
(2)
则最优控制可以表示为
(3)
其方法有很多种,本文利用近似值函数的方法来实现整个算法过程,这可以很好地解决动态规划的维数灾问题。近似动态规划变量说明见表1。

表1 近似动态规划变量说明Table 1 ADP symbology
2 算法构架
算法的基本函数是状态转移函数,将目标追踪的过程离散化,则每个状态到下一个状态由状态转移函数控制。而奖励函数、特征生成函数、轨迹采样函数等都用来生成近似值函数,值函数即状态的未来奖励值,奖励值越大,则对于无人机来说位置就越好,可以通过近似的值函数产生最佳策略。算法框架如图2所示。
2.1 状态量、目标、控制量以及动力学
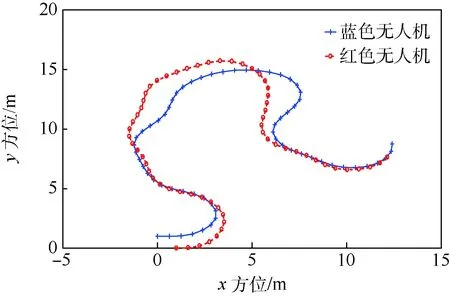
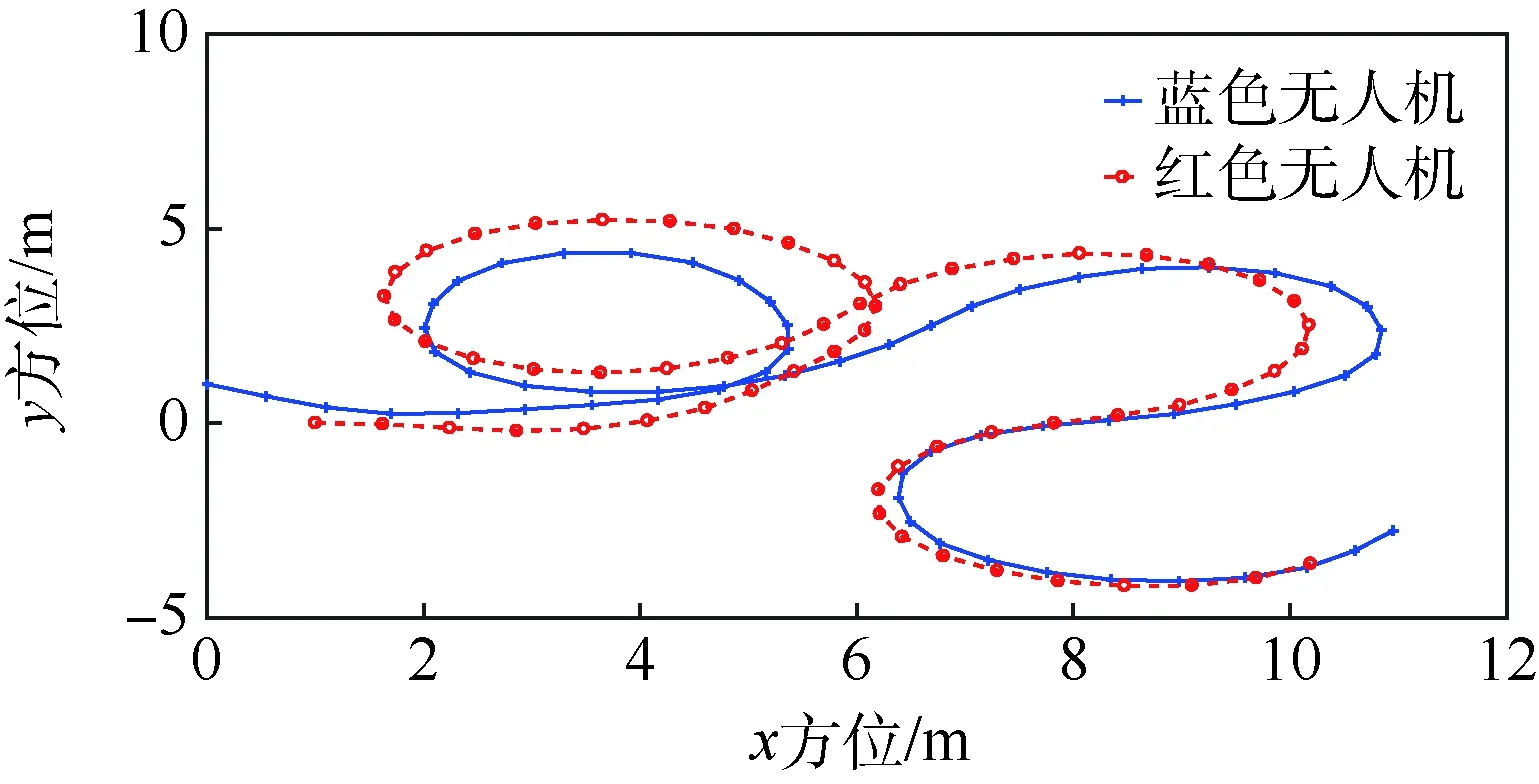
跟踪系统的状态量x由无人机和目标的位置、偏航角和滚转角组成,本文目标可以指具有滚转角特征的比如其他飞行器、鸟类等,如果为其他不具有滚转角的目标,则可替代为控制量直接作用的状态量。本文选取的是具有滚转角的对象,以我方飞行器为蓝色无人机,目标用红色代替[13]。
(4)
式中:ψ为偏航角,下标b和r分别表示蓝色和红色无人机;φ为滚转角;xpos和ypos可以在x-y平面内任意取值,滚转角和偏航角需要在[-180°,180°]取值。
跟踪的目标始终在一定范围之内,有时候还需要其他的目标来满足需求,比如必须把无人机限制在目标后方的一定扇形区域内,以保证我方无人机占据优势的战略地位。还有其他需求,比如跟随航拍,就必须把无人机限制在目标前方的扇形区域内,本文设定的目标是在其后方的扇形区域内。具体区域如算法1所示,AA和ATA分别为方位角和天线拂擦角。奖励区域如图3所示。
算法1优势位置函数gpa(x)
输入:{x}。
R=“飞行器与目标的欧几里得距离”
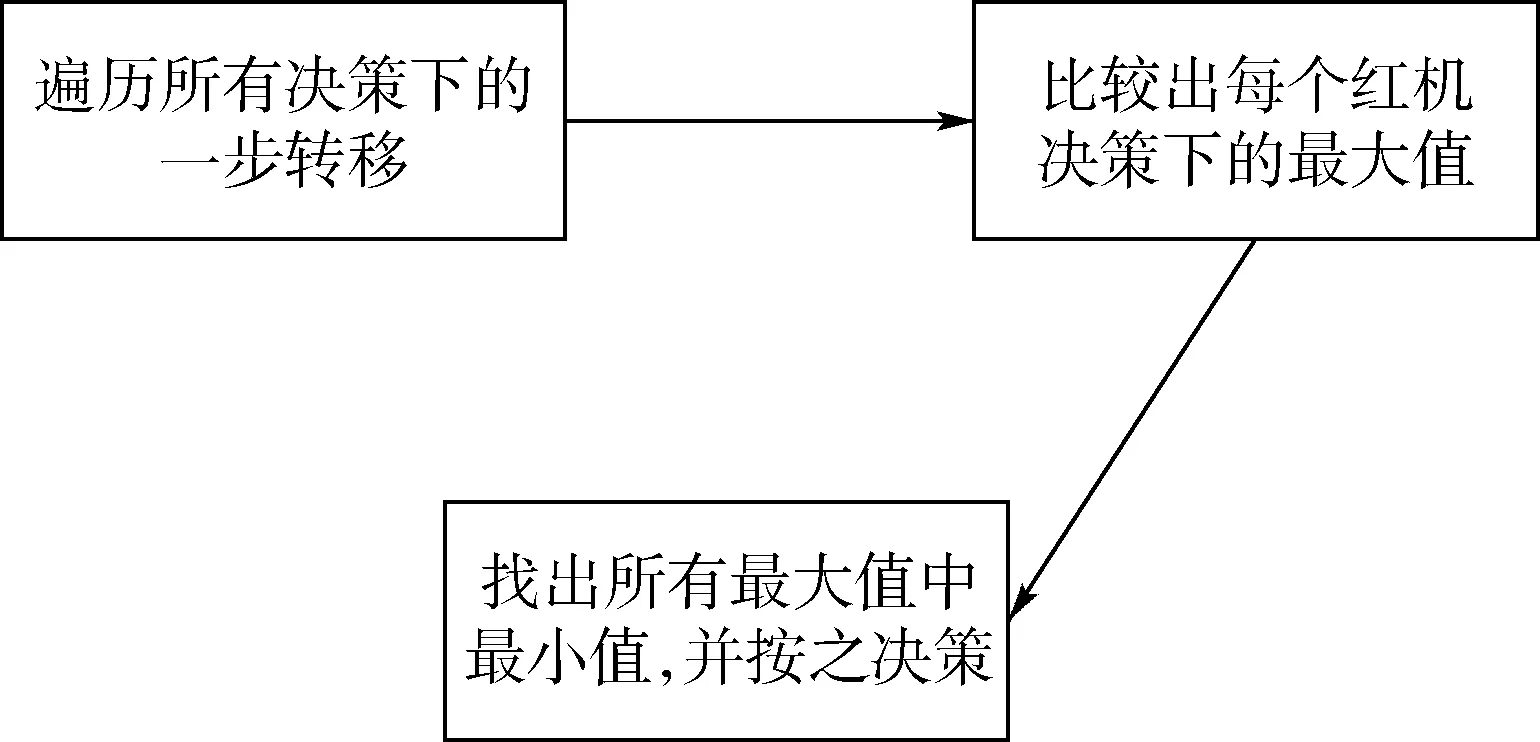
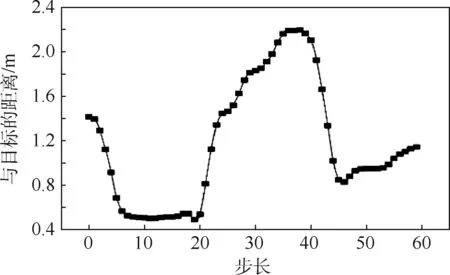
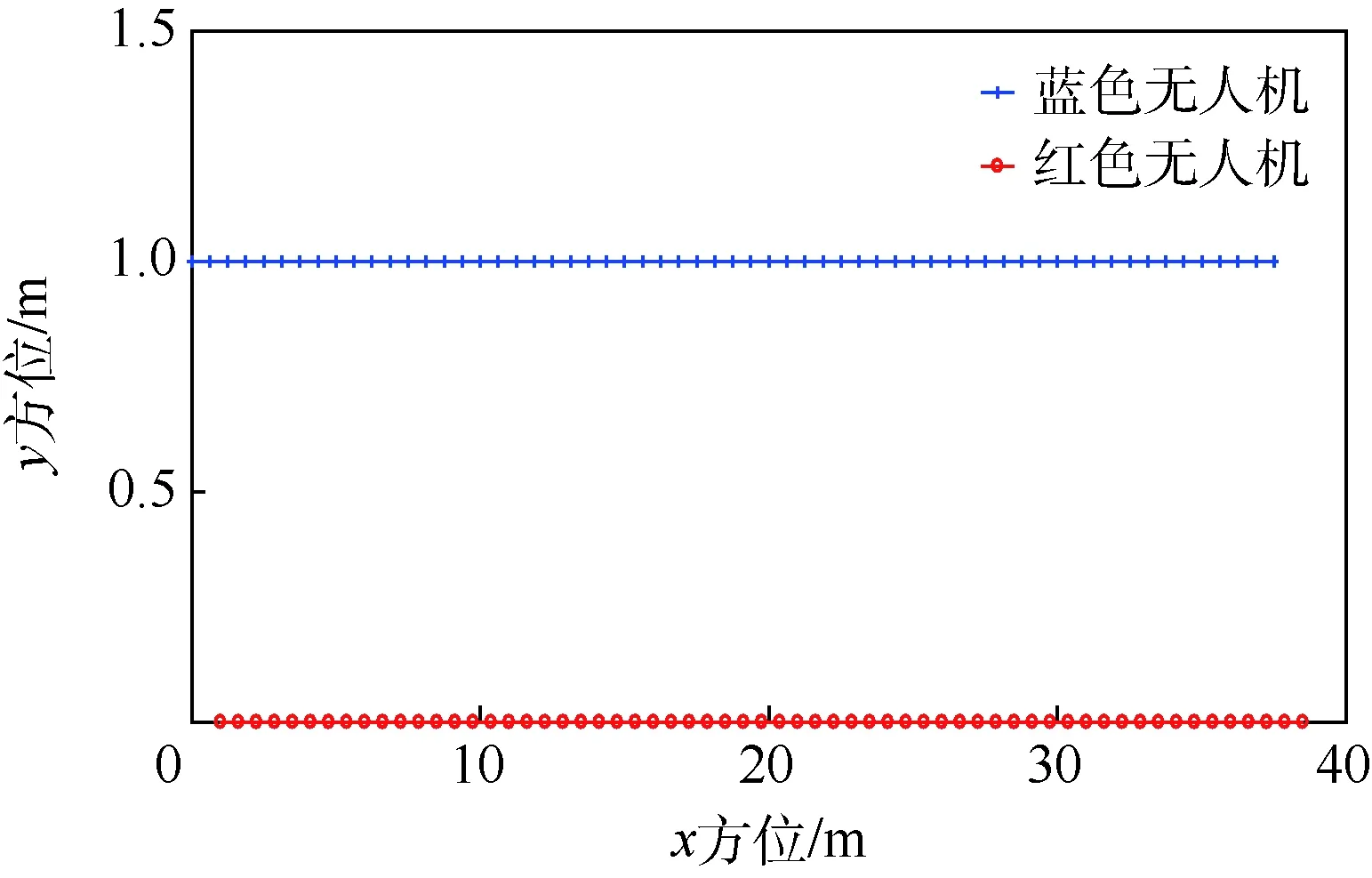
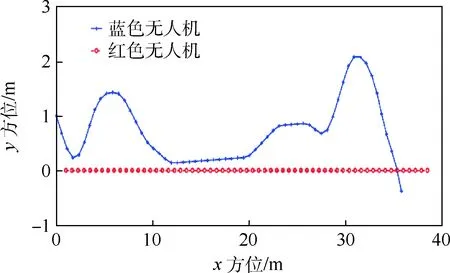
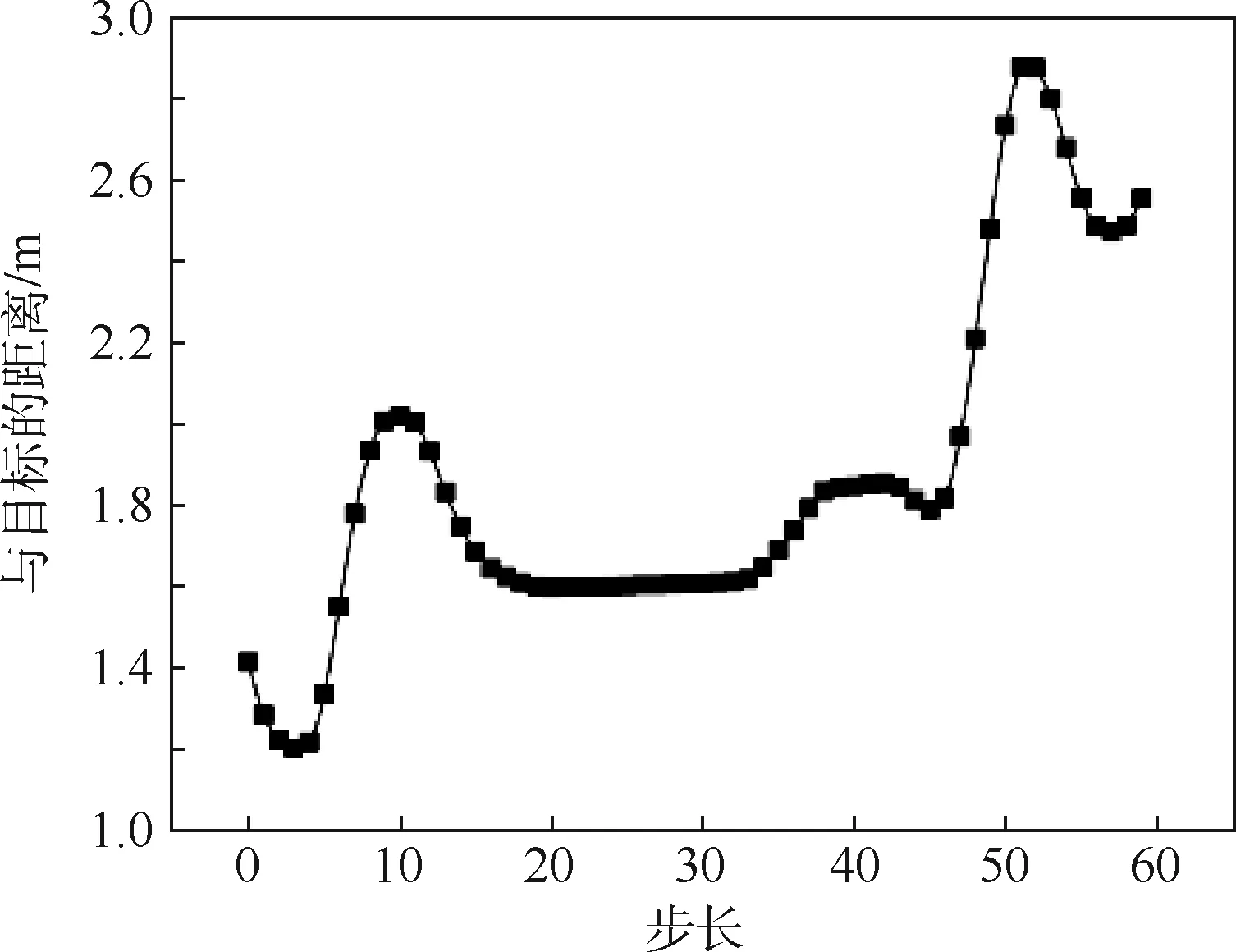
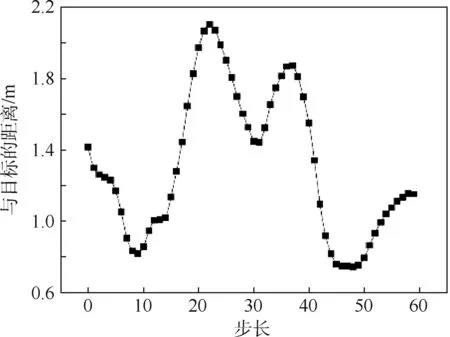
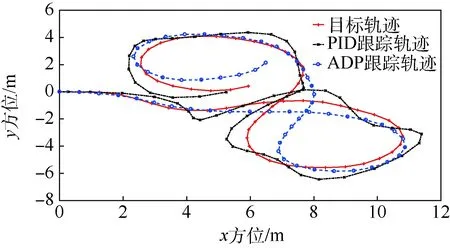
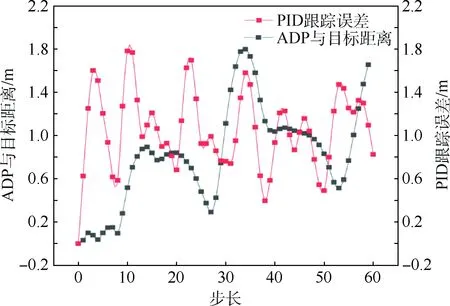
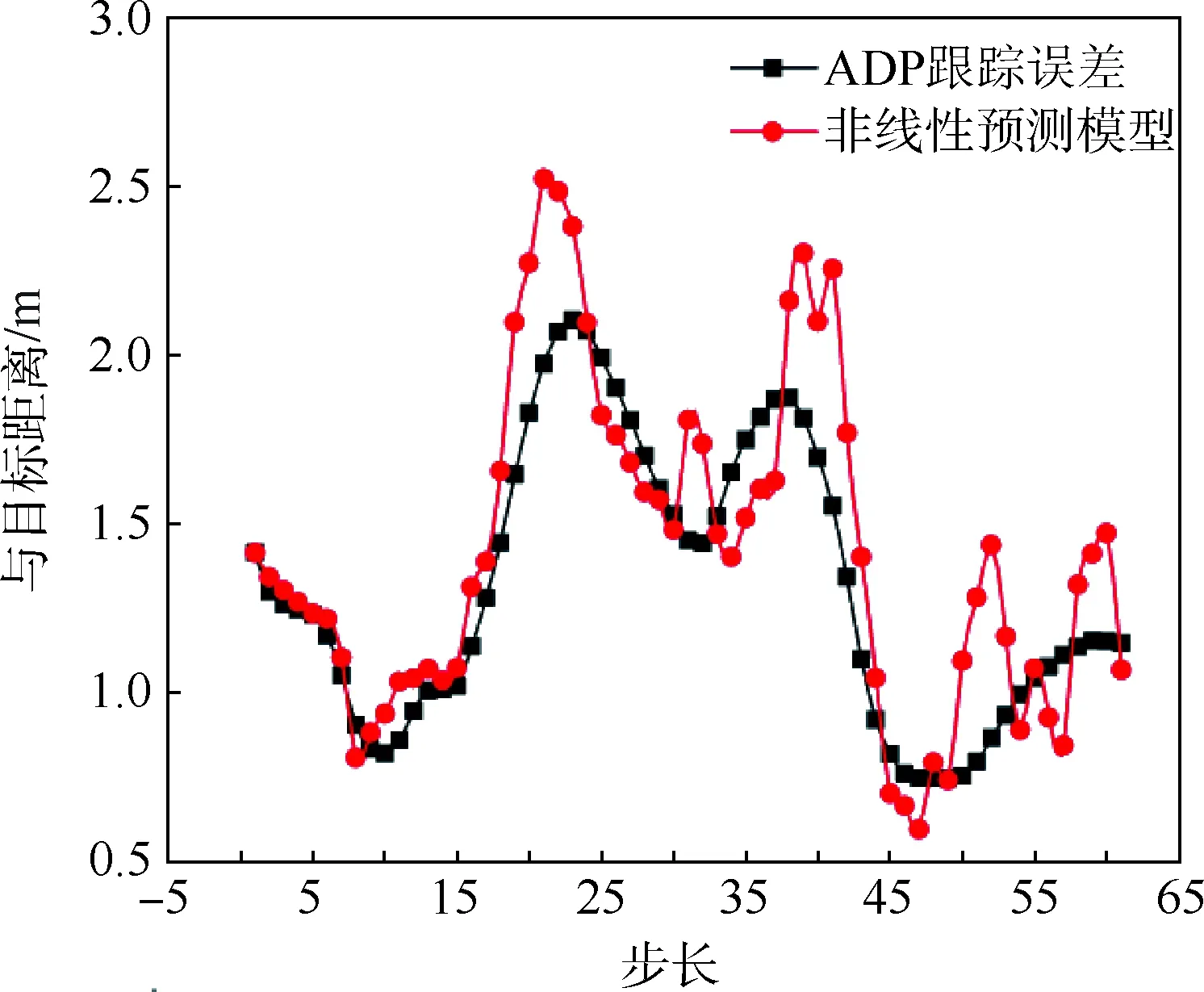
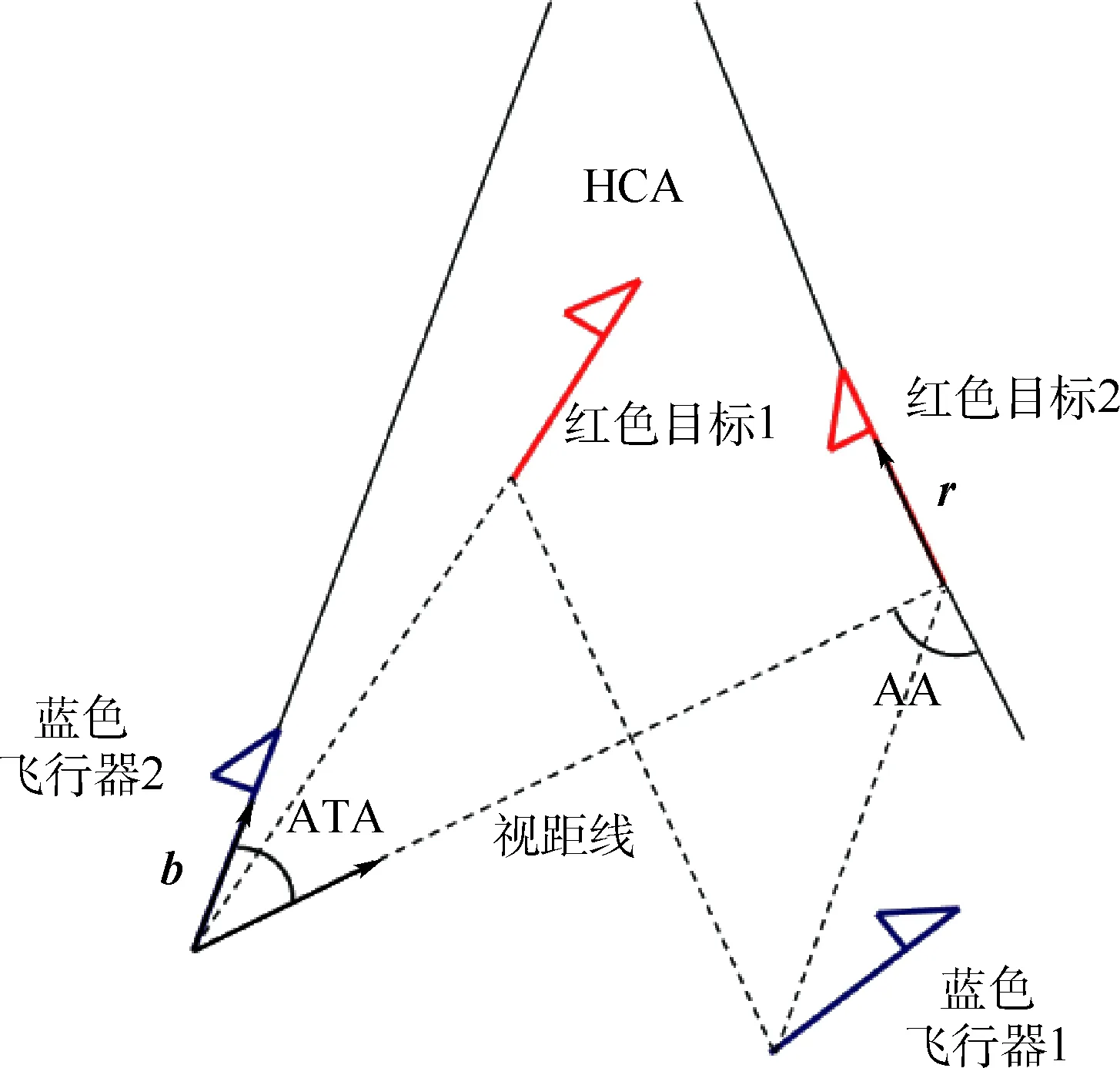
if(0.1 m (|ATA|<30°) then gpa(x)=1.0 else gpa(x)=0 end if 输出奖励:(gpa)。 图2 算法框架Fig.2 Algorithm framework 图3 奖励区域Fig.3 Reward area 算法2状态转移函数f(xi,ub,ur) 输入:{xi,ub,ur}。 fori=1:5(once per Δt=0.05 s) do for{red,blue} do ifu=L then else ifu=R then end if ypos=ypos+Δtvcosψ end for end for 为了更好地训练无人机的跟踪效率,本文使用极大极小算法使跟踪目标与我方无人机进行博弈。而对于每个状态,我方及目标皆有3个机动策略,所以有9种可能的结束状态,红色目标的机动策略选择源自双方的初始状态与9种可能情况的结合机动策略,通过状态转移函数计算结束状态。而在每个状态采用一种评分体系对当前位置进行评分,表示红色目标的优势程度,因此,我方无人机的目标就是最大化地减小其评分。 按照目标的定义,跟随在目标的后方的一定距离以内,可以得到优势位置函数gpa(x),可是它的不连续性导致近似值函数过程难于操作,所以引入连续的评估函数S(x),将两者结合起来一起构成每个状态的评分体系[14]。 评估函数表达式为 (5) 每架飞行器都有相对于另一架飞行器的对称表示,不失一般性,本文从蓝色飞行器角度描述几何。奖励区域为两箭头所夹区域,ATA为我方无人机头部与视距线的夹角,AA为视距线与敌方无人机头部反方向所成夹角。R为两物体之间的实际距离,Rd为两物体间的期望距离,常数p单位为m/(°),其为用来协调方位分数和距离分数。p的有效值为0.1 m/(°),R的有效值为2 m。目标奖励函数的具体表达式为 g(x)=wggpa+(1-wg)S (6) 式中:wg=0.8为权重系数。 图4、图5分别给出了评估函数以及具体奖励位置的三维图。假设目标在原点。 图4 评估函数Fig.4 Evaluation function 图5 优势目标奖励的位置Fig.5 Advantageous target reward position b=[cosψb,sinψb]T (7) r=[cosψr,sinψr]T (8) AA=arccos(dbrb/(dbrb)) (9) ATA=arccos(dbrr/(dbrr)) (10) (11) 图6 角度定义Fig.6 Angle definition (12) 这些被选取的特征被用来形成特征向量ζ(x),特征量通过相互组合进行扩充,举个例子,如果选取的特征量为{A(x),B(x),C(x)},则形成的特征向量为 ζ(x)=[A(x),B(x),C(x),A(x)B(x), A(x)C(x),C(x)B(x),A2(x), B2(x),C2(x)] (13) 则在第k次迭代后,值函数可以被近似为 (14) 式中:βk为各个特征对于近似值函数的权重系数。可以看出,如果特征量选取越多,则近似值函数对于真正值函数更为接近,但是由此可以看出,特征量选取的越多,则计算的复杂度和量要大大增加,这违背了本文选取近似动态规划的初衷。所以选取上述对于目标跟踪十分重要的特征,总计如下[15]。 (15) 采样点越密集则对于近似值函数来说就更加精确,但是对于计算量来说,采样点越密集,计算量就越大,因此应选择采样区间。 为了使采样的空间更加符合目标跟踪时的实际情况。我方无人机以及跟踪目标的横纵坐标使用标准差为7 m的高斯分布,初始状态的偏航角以及滚转角符合均匀分布。就像最小二乘法中所使用的方法,将所有采样的状态存储于一个大矩阵X中。 (16) 使用生成的采样点生成构建近似动态规划框架的特征为 ζ(x)=[ζ(x1),ζ(x2),…,ζ(xn)]T (17) 为了更好地训练值函数,使得训练出来的值函数具有最大的普遍性,目标运动算法选择博弈算法,本文采用Minimax算法,Minimax算法又名极大极小算法,是一种找出失败的最大可能性中的最小值的算法[16]。 Minimax算法常用于棋类等由两方较量的游戏和程序。该算法是一个零总和算法,即一方要在可选的选项中选择将其优势最大化的选择,另一方则选择令对手优势最小化的方法。而开始的时候总和为0。其算法如图7所示。 图7 Minimax算法流程Fig.7 Minimax algorithm flowchart 通过合理的轨迹采样、特征选取以及奖励函数的建立,可以通过算法得到一个与真实值函数十分近似的近似值函数。其具体思想如下所示。 假设λ是列向量的系数,本文可以把整个模型[17]写为 y=λTx+ε (18) 式中:y、x和ε分别为因变量、自变量和估计误差。 (19) (20) 那么本文的目标变为选择一个β使误差的平方和最小,即 (21) (22) 则通过以上方式,本文可以得到近似值函数,算法大概通过40次迭代,可以得到最优的参数矩阵。 尽管本文的近似值函数相对于真正值函数来说已经十分接近,但对于策略选择来说,仍有可能不是最优的策略,所以策略选取应用rollout策略[18]。rollout算法是对于当前状态,从每一个可能的动作开始,之后根据给定的策略进行路径采样,根据多次采样的奖励和来对当前状态的行动值进行估计。在当前估计基本收敛时,会根据行动值最大的原则选择动作进入下一个状态再重复上述过程。在蒙特卡罗控制中,采样的目的是估计一个完整的,最优价值函数,但是rollout算法中的采样目的只是为了计算当前状态的行动值以便进入下一个状态,而且这些估计的行动值并不会被保留。在得到最优的策略函数后也可将结果放入神经网络训练,利用决策对特征进行分类,使得无人机在博弈或者跟随目标的程中快速做出决策。算法具体实现过程如算法3所示。 算法3rollout算法 输入:xi。 初始化:Jbest=-。 forub={L,S,R} forj={1:Nrolls} do end for ifJcurrent>Jbest then ubest=ub,Jbest=Jcurrent end if end for 输出:ubest。 对定常运动的目标以及与我方无人机博弈的目标的跟踪任务进行了仿真,任务是始终在目标的后方的0.1~3 m,最后将本控制算法与经典控制算法PID进行比较,得出本算法在复杂环境下的优势。 通过之前所叙述的利用博弈离线训练好近似值函数特征参数的方法,结合rollout算法,可以得到最优的控制指令。 通过给定两方无人机不同的初始状态以及选取目标无人机的不同策略,来模拟不同环境的工况,初始状态以及目标策略选取如表2所示,其中,Minimax代表目标无人机选取与我方博弈的极大极小策略,Maintain代表目标无人机选取定常的直线运动。 最后,对比本文与传统PID算法的仿真结果, 由于PID算法只能跟踪预定轨迹,在进行PID算法的仿真时,将ADP仿真完成后得到的目标轨迹给定给PID算法,从而比较出本文算法优势。仿真结果如图8~图20所示,xinit为起始状态分类。各仿真图初始状态及目标策略如表2所示。 由以上仿真结果可知,如果已知目标的位置,目标的运动是定常的,如图11、图13所示可以实现很好的跟随,并且按照预定的目标始终跟在目标的后方,而对于目标运动变化较大,甚至与我方进行博弈的情况下如图9、图15所示,由仿真图所示,该算法具有一定的预测性,该控制算法可以实现很好的跟随。与给定PID目标轨迹的控制方法比较,可以看到,即使给定传统PID算法目标轨迹,其跟踪的稳定性也不是很好,具有一定的振荡,但对于ADP算法,从图16中可以看出其具有一定的预测性,且其与目标的距离始终保持在之前设定的0.1~3 m的范围以内,不妨假设ADP跟踪的目的为与目标为1 m,而PID的目的为与 目标的距离为0 m,可以计算得到各算法的方差分别为 表2 各仿真图初始状态及目标策略Table 2 Initial state and objet strategy of each simulation chart 注:πr—敌机机动策略。 图8 60步长仿真(xinit=1)Fig.8 60 step length simulation (xinit=1) 图9 实时与目标距离(xinit=1)Fig.9 Real-time target distance (xinit=1) 图10 60步长仿真(xinit=2)Fig.10 60 step length simulation (xinit=2) 图11 实时与目标距离(xinit=2)Fig.11 Real-time target distance (xinit=2) 图12 60步长仿真图(xinit=3)Fig.12 60 step length simulation chart (xinit=3) 图13 实时与目标距离(xinit=3)Fig.13 Real-time traget distance map (xinit=3) 图14 60步长仿真(xinit=4)Fig.14 60 step length simulation chart (xinit=4) 图15 实时与目标距离(xinit=4)Fig.15 Real-time traget distance map (xinit=4) 图16 给定PID目标轨迹时的仿真比较Fig.16 Simulation comparison when PID target trajectory is given 图17 PID跟踪误差以及ADP与目标距离Fig.17 PID tracking error and target distance from ADP simulation 图18 非线性预测模型方法与ADP的跟踪比较Fig.18 Comparison of tracking between nonlinear prediction model methods and ADP SADP1=52.994 5 m2 (23) SPID=75.183 5 m2 (24) SADP2=114.7 m2 (25) Snolinear=136.9 m2 (26) 在这组仿真下可知,即使在ADP算法不知道目标的轨迹的前提下,ADP算法也具有更好的稳定性。由此可知,该算法可以适应于较为复杂的环境。 图20所示的是基于非线性模型预测跟踪控制算法的逃逸无人机控制[17-19],由图可知,虽然 这种算法有着较好的跟踪结果,但是由于这种方法本身不产生机动,所以该方法有着一个天然的缺陷,它不具有在追踪和逃逸角色切换的能力。而ADP算法可以很好地实现角色的切换。 图19 非线性预测模型方法与ADP的跟踪误差比较Fig.19 Comparison of tracking error between nonlinear prediction model method and ADP 图20 无人机跟踪与博弈Fig.20 UAV tracking and gaming 1) 本文对无人机跟踪控制算法进行研究,提出了将近似动态规划用于目标跟踪问题中的飞行控制问题,在已知双方状态的条件下,可以应对目标的灵活运动,预测目标的运动轨迹。 2) 为了确保得到的决策是最优决策,使用rollout算法得出结论。实现了飞行器在跟踪甚至博弈过程中的有效跟踪,在现行跟踪问题上缺少飞行控制的研究进行了补充。 3) 仿真验证了目标跟踪的有效性。对于多目标且多控制体的模型可以结合粒子群算法、遗传算法等其他智能算法[20]来实现。项目可以应用于大多数跟随场合以及大多数飞行器博弈场合。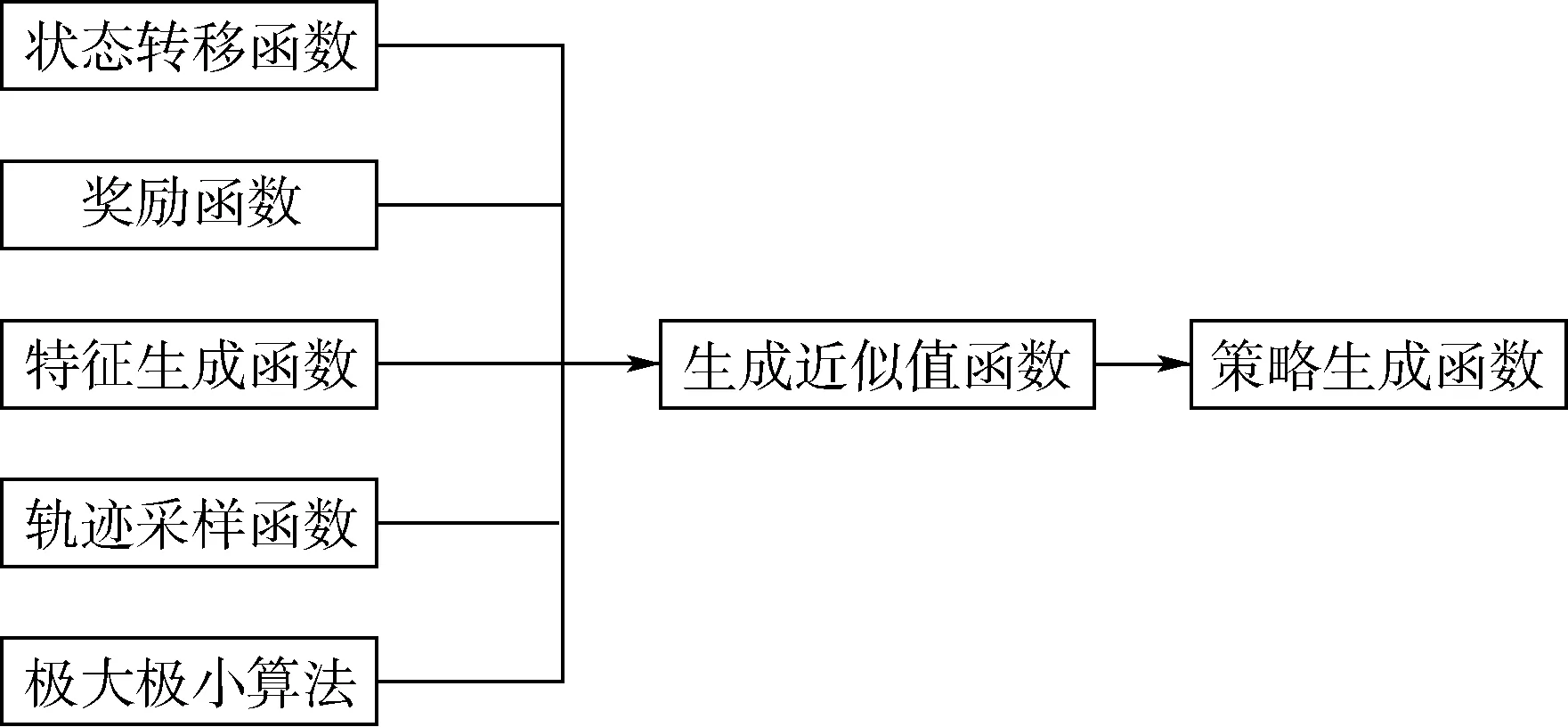
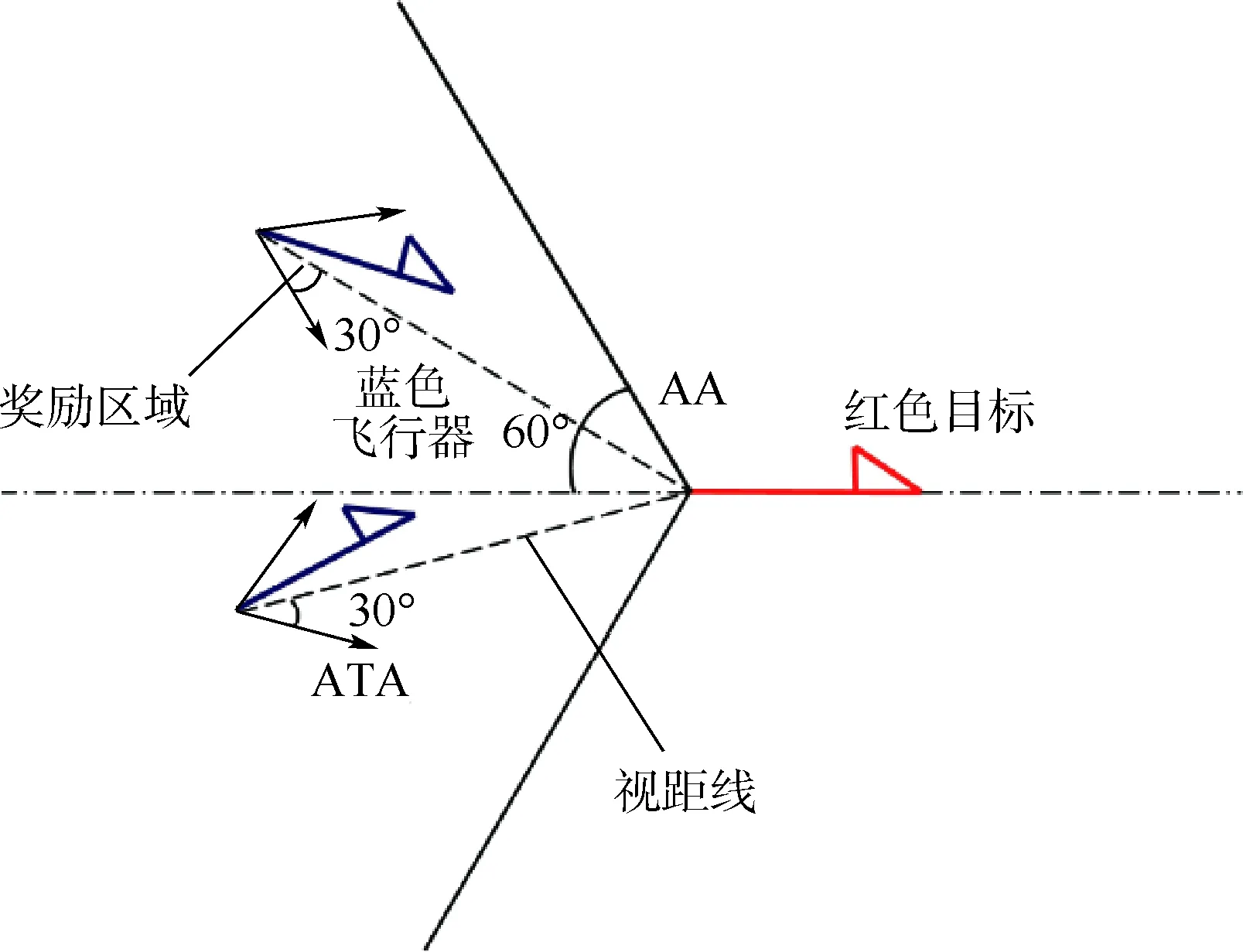
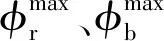
2.2 奖励函数
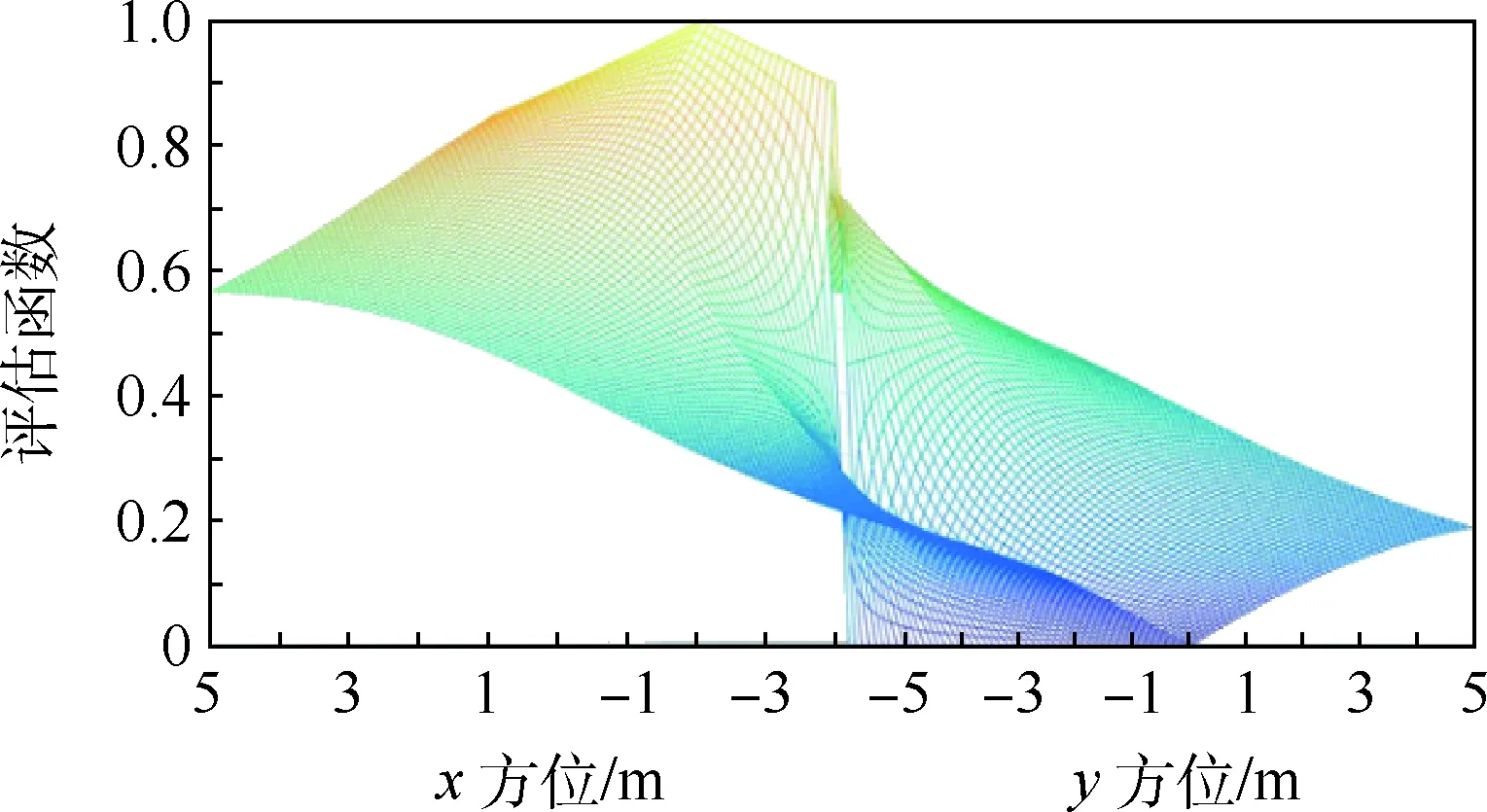
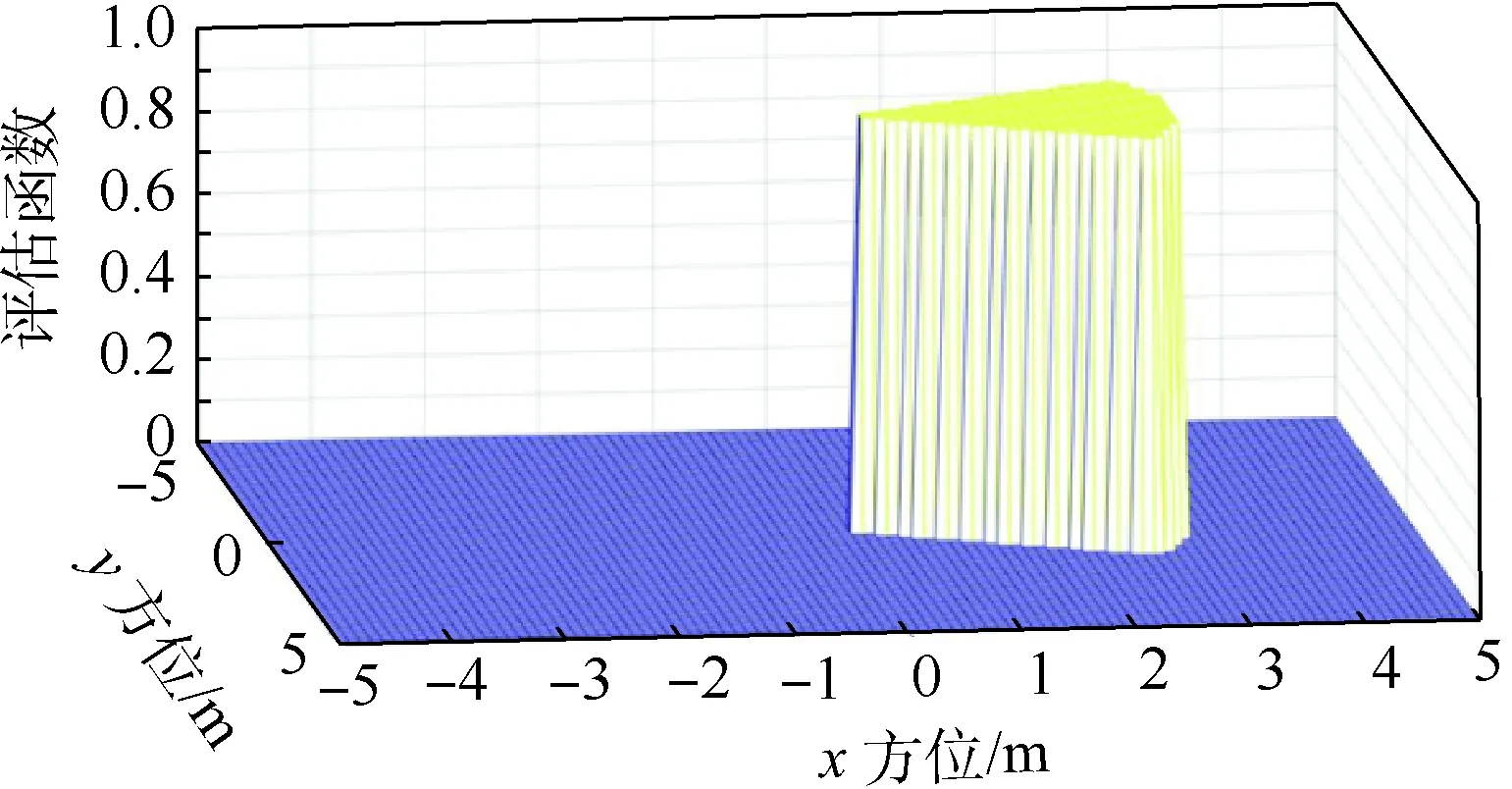
2.3 特征选取
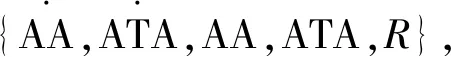
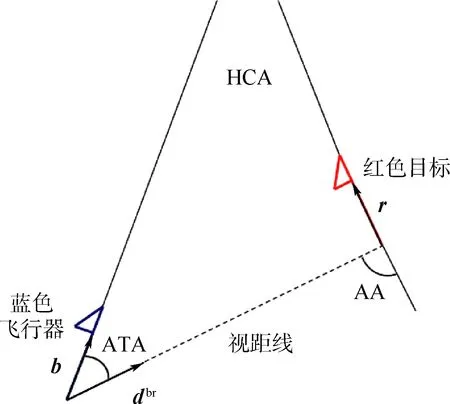
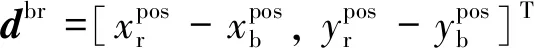
2.4 轨迹采样
2.5 目标策略函数
2.6 生成近似值函数
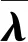

2.7 策略选取(控制指令生成)
3 仿真结果



4 结 论
