基于蒙特卡洛遗传算法的排课问题研究

张贵军, 陈 安, 胡 俊

(浙江工业大学 信息工程学院, 浙江 杭州 310014)

随着高等院校招生规模扩大和专业的发展,教学资源不足的问题被放大,合理的教学安排变得尤为重要。排课已经成为教学管理中的一项重要工作[1]。

排课问题实质上属于调度问题的研究范畴,即将班级、教师、课程等资源根据约束条件安排在特定的时间和教室中,并使结果达到最优。由于该问题具有多约束、多目标和非线性的属性[2],难以用经典优化方法求解,因此通常采用启发式优化算法,例如模拟退火算法、遗传算法、禁忌搜索算法等来求解该类问题[3]。

笔者对传统遗传算法做了改进,提出一种基于蒙特卡洛的遗传算法,对交叉和变异阶段产生的个体采用蒙特卡洛概率接受的方法,弥补传统遗传算法的早熟、收敛速度慢等缺点,避免算法陷入局部极值解,提高种群的质量。最后,采用ReactJS+NodeJS+MongoDB框架开发出一套智能排课系统。

1 排课问题的数学模型

排课问题的主要内容是将班级、课程、教师和教室安排在不冲突的时间内。然而在排课过程中,课表的合理性会受课程时间安排均匀度、教室利用率以及不同类型课程在不同时间段上课效率等方面的影响。因此,排课需要解决的问题是：确定每个班级的课表在满足各种约束的条件下目标达到最优。

1.1 变量描述

排课问题的数学模型变量描述为：

(1) 班级集合：C={c1,c2, …,cn}；

(3) 教师集合：T={t1,t2,…,tk}；

(5) 教室集合：R={r1r2,…,rp}；

(6) 教师对上课时间的满意度集合：W={w1,w2,w3,w4,w5}。

1.2 约束条件

在建立排课问题数学模型之前,考虑如下约束条件[4-6]：

(1) 同一个班级在同一个时间段只能安排一门课程,即：

(1)

表示同一个班级cn在同一时间dm只能安排同一门课程kl,在教室rp由教师th授课；其中L表示最多有L个课程,H表示最多有H个教师,P表示最多有P个教室；

(2) 同一个教师在同一时间段只能安排一门课程,即：

(2)

表示同一个教师th在同一时间dm只能安排同一门课程kl,在教室rp授课班级cn；其中L表示最多有L个课程,N表示最多有N个班级,P表示最多有P个教室；

(3) 同一个教室在同一时间段只能安排一门课程,即：

(3)

表示同一个教室rp在同一时间dm只能安排同一门课程kl,在教室中由教师th在授课班级cn；其中L表示最多有L个课程,N表示最多有N个班级,H表示最多有H个教师；

(4) 教室容量须大于班级学生人数,即：

rnum≥cnum

(4)

rnum表示教室容量,cnum表示班级学生数量。

(5) 每个课程的上课时间尽量满足教师的要求；

(6) 同一门课程的上课安排不能过于紧凑；

(7) 合理利用教室的利用率与上课地点的关系。

上述(1)—(4)为排课的硬约束条件,(5)—(7)为软约束条件。满足硬约束条件的方案便是排课的可行解,软约束条件则是作为评判排课方案好坏的标准。本文的排课方法是在对班级、课程、教师、教室和学生五元数组求解过程中,满足上课地点和上课时间不冲突的条件下,经过一步步的优化最终找到最优的排课方案。

2 编码方案

2.1 编码

编码方式不同,排课效率也会不同,好的编码方式能够让排课变得更高效。本文中,排课问题的研究对象为班级、课程、教师、时间和教室,采用十进制的编码方式对课表编码。

将课表看作个体,将班级、课程、教师、时间和教室信息编码作为染色体,编码结构形式为班级编号-课程编号-教师编号-上课时间编号-教室编号(见图1)[7]。例如编码为0113-0301-0202-1135-1204,表示班级编号为0113的班级,由编号为0202的教师来授课编号为0301的课程,“1135”表示上课时间,规定一门课程一周上2个课时,将一天划分为5个上课时间段,所以“1135”表示为周一的第1段时间(即上午第1、第2节课),以及周三的第5段时间(即晚上第9、第10节课)。

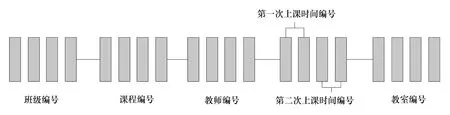
图1 基因编码图

2.2 适应度评价函数

在遗传算法中,适应度评价函数是衡量一个个体好坏程度的重要标准。本文将从3个方面对排课问题定义评价函数。

2.2.1 课程间隔

对于同一门课程的安排,合适的时间间隔有助于学生学习和巩固课程知识,保持学习的积极性,同时给予教师充分的时间备课,避免学生与教师因密集的课程而过度劳累。

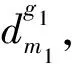
(5)

(6)

(7)

(8)

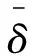
2.2.2 教室间隔

一天内相邻时间的上课教室安排对学生和教师也有一定的影响,合理安排上课教室能够使学生在上课之前有充裕的时间休息和预习下一节课程内容,让教师有充足的时间休息并且准备上课内容。因此针对教室间隔的安排,具体方式如下：

(9)

(10)

(11)

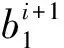
2.2.3 教师要求

课程安排的时间和地点应尽可能满足教师的要求,如果上课时间和地点与教师的个人安排有冲突,会导致教学进程缓慢、教学效率降低。因此,满足教师对上课时间和地点的要求是教学排课中一个重要的环节。教师合理度要求表达为

(12)

其中,f3表示总的教师合理度,q表示一个班级的教师合理度,θ1表示根据第一次上课时间段从教师-时间满意表中查询其对应的满意值,θ2表示根据第二次上课时间段从教师-时间满意表中查询其对应的满意值,如表1表示教师A的时间满意表；α表示教师对安排的授课教室的满意度,其值也是通过查找教师-教室满意表得到,如表2表示教师A、B、C对教室A、B、C、D、E的满意表。

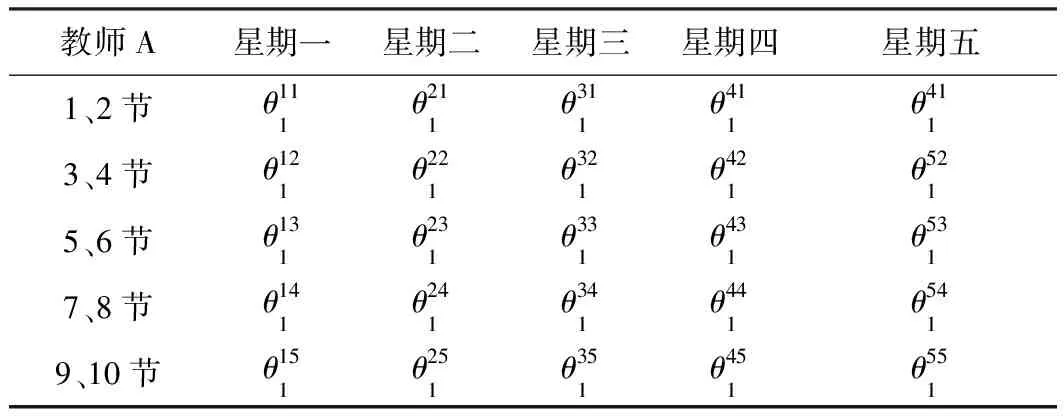
表1 教师-时间满意表

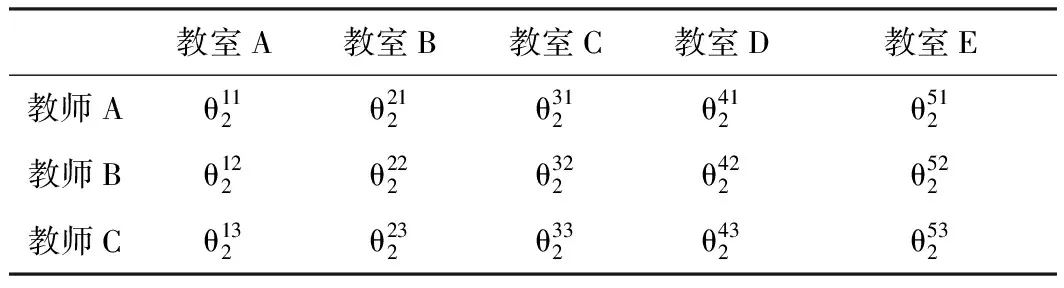
表2 教师-教室满意表

综上所述,本文的适应度评价函数F定义如下：

(13)

其中ωi表示适应度函数评价值fi对应的权值,其中i=1,2,3,因此目标函数为f=max(F)。

3 蒙特卡洛遗传算法

3.1 蒙特卡洛

本文的排课问题实质可定性为一个离散非线性规划问题。在排课中,蒙特卡洛[8-10]采样过程如下：

首先,设定马尔可夫链状态转移概率ρ与当前种群最优个体状态值x0以及新生成个体状态值x1有关,平稳分布π(x)设定状态转移次数的阈值为n1。

然后,在每一次遗传算法排课的迭代过程中,进行n1次转移：

(1) 从均匀分布中u～uniform[0,1]中随机采样得到u；

(2) 若u<ρ,则接受转移x1→x0并且结束本次转移,则x1=x2,其中x2表示下一代新个体的状态值；否则不接受转移。

3.2 种群初始化

传统遗传算法在初始化种群过程中,通常采用随机方案来生成种群。考虑排课的特殊性,本文在初始化过程中加入约束条件生成初始化种群。

根据教学任务,班级的专业课和授课教师已经提前安排,只需对上课时间和上课地点初始化。首先,对于每个班级随机生成一组课程的上课时间和地点。若分配的上课时间、教室位置以及教室容量没有发生冲突,那么将信息保存下来作为个体中的一条染色体；若产生冲突,则按照上述规则重新初始化,依次完成每个班级的编码直到全部成功编码,最终根据种群规模来生成相应个体,从而达到种群初始化。

3.3 选择

选择操作是对种群中个体进行去劣存优的一种自然选择过程,从旧种群中选取适应性强的个体。个体适应度越高,被选择的可能性越大[11]。本文采用蒙特卡洛概率接受的方法进行选择,若交叉变异产生的新个体优于旧个体,则接受该个体,否则以一定的概率来接受该个体,其中接受概率为

(14)

其中σ为接受概率,E1为旧个体的适应度,E2为新个体的适应度,KT为常量；

3.4 交叉

染色体的交叉保证了种群的多样性,防止遗传的单一化[12],在进行交叉之前要选择双亲。本文中选取当代种群中适应度最优的个体S1作为父代,在剩余个体中随机选择个体S2作为母代。交叉的方法为：

(1) 从双亲中随机选取2段相同片段的染色体,将染色体中的“时间”和“教室”基因如图2方式进行交换；

(2) 判断交换成功之后的个体S1是否发生课表冲突,若不冲突,则表示交叉完成,否则恢复染色体片段并且回到步骤(1)中继续交叉,直到不冲突。

图2 交叉

3.5 变异

变异操作是自然选择中的突发过程,它的出现扩大了种群的多样性[13]。本文中的变异方式有3种：对染色体中的“时间”进行变异；对染色体中的“教室”进行变异；对染色体中的“时间”和“教室”基因一起变异[14]。具体变异操作如下：

(1) 首先通过生成随机数来判断执行上述变异方式中的一种；

(2) 从个体中随机选取一条染色体进行变异,其中变异的方式如图3所示,从时间集合D或者教室集合R中随机选取时间和教室编号信息,替换该染色体中的时间和教室编号；

(3) 判断变异之后的个体是否发生课表冲突,若不冲突,则表示变异完成,否则转到步骤(2),并且恢复该染色体片段。

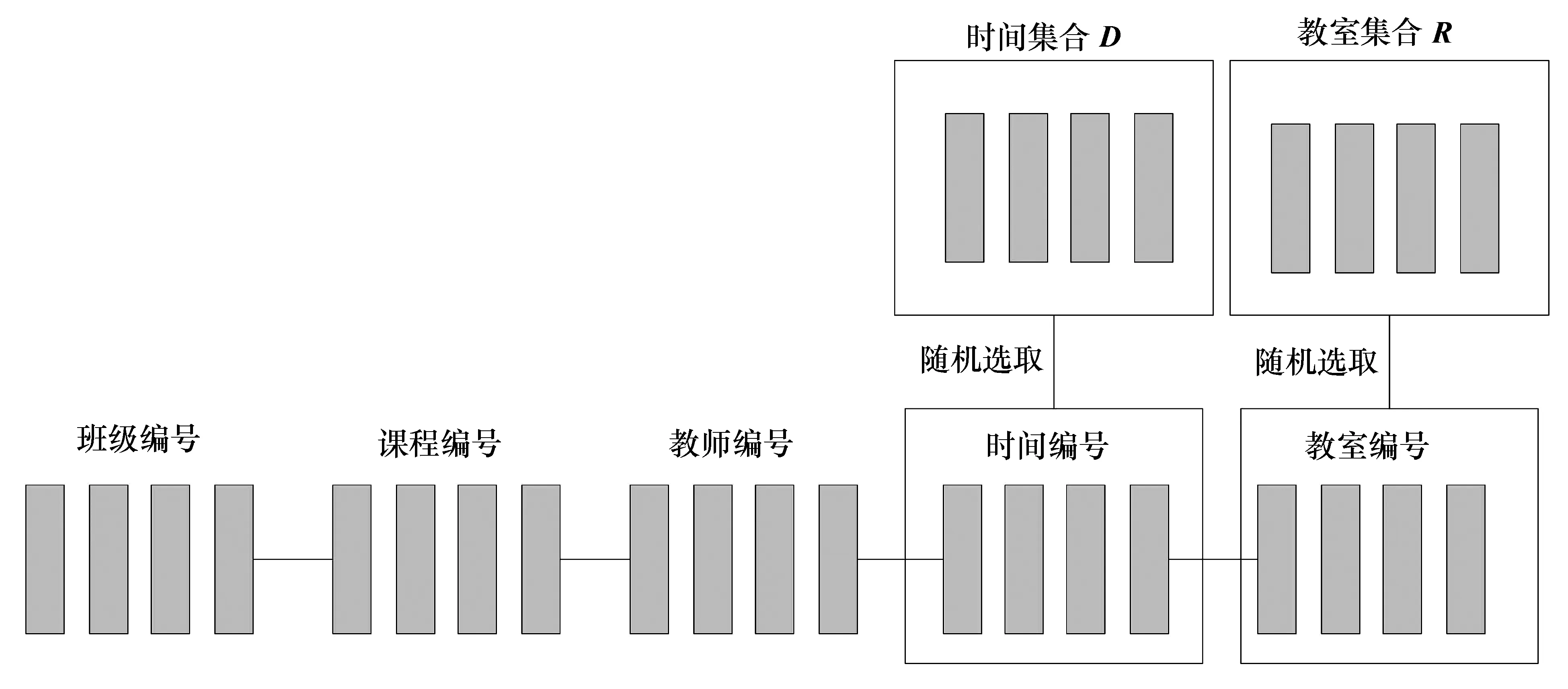
图3 变异

4 仿真测试与分析

为了验证排课问题中蒙特卡洛遗传算法的性能,选取某高校某学院27个班级、55位教师的实验数据。将教师对于时间和教室的满意值均设为1,设置种群规模20,交换概率0.5,变异概率0.01,遗传代数1 400代。将传统遗传算法与基于蒙特卡洛遗传算法作对比测试,运行结果如图4所示。从图4中可知,在1～400代期间,传统的遗传算法对适应度的提升稳定,而蒙特卡洛遗传算法对适应度的影响影响较大,适应度的变化体现出蒙特卡洛方法中对较差适应度个体进行概率接受的特点,在400～1600代的时候,基于蒙特卡洛的遗传算法收敛速度优于传统遗传算法。实验结果表明：基于蒙特卡洛的遗传算法得到的最优解优于传统遗传算法,说明加入蒙特卡洛方法可以避免局部极值解,得到问题最优可行性方案。

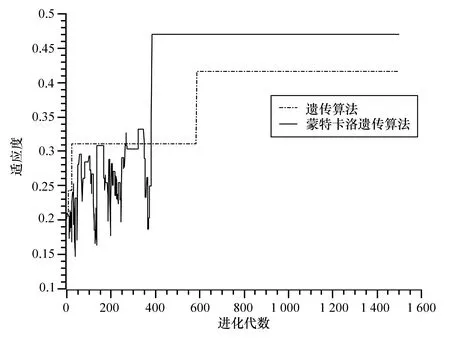
图4 蒙特卡洛遗传算法收敛性能对比图

5 结语

排课是教学管理中非常重要的一部分,传统的排课方法效率低、排课冲突率高,影响教学秩序。本文采用基于蒙特卡洛的遗传算法进行排课,统计学生、教师、课程等信息,将排课问题转化成多约束、多目标的模型优化问题,将蒙特卡洛与遗传算法结合,启发式搜索排课问题的最优可行性方案,在满足上课时间、地点不冲突,兼顾学生、教师和教室容量需求的情况下得到比较人性化、合理化的课表。