基于等几何边界元法的声屏障结构形状优化分析

陈磊磊， 申晓伟， 刘 程， 徐延明

(1. 信阳师范学院 建筑与土木工程学院，河南 信阳 464000； 2. 中国科学技术大学 近代力学系， 合肥 230026)

声屏障作为一种有效、经济的降噪工具，在交通噪声治理中已被广泛采用，如何有效地利用好这一降噪措施，使其发挥出更大的经济技术效果，对于改善人们的生活质量具有重要的意义。声屏障的降噪效果与声屏障的形状、尺寸和材料属性有关，进行声屏障结构优化设计可以有效地提高其降噪效果。目前大多研究都集中在采用遗传算法等启发式算法进行声屏障的形状优化例如，Baulac等[1]采用遗传算法对T型声屏障的顶端结构进行了优化设计；Toledo等[2]采用了进化算法对声屏障顶端形状进行了优化；Mun等[3]采用了模拟退火方法对声屏障的几何尺寸进行了优化。这些研究大多采用传统几何插值方法描述结构形状，在优化过程中很难灵活地控制形状变化，并需进行网格再划分。由于这些缺点，现有研究大多对几何形状较为简单的顶端结构进行优化[4]。等几何方法(Isogeometric Analysis，IGA)可以克服这些缺点，该方法采用CAD(Computer Aided Design)领域中广泛使用的非均匀有理B样条(Non Uniform Rational B Sample，NURBS)进行几何建模，并在CAE(Computer Aided Engineering)分析中采用相同的样条基函数进行物理场插值计算，实现了几何模型与分析模型的同一表达。与传统算法对比，具有以下优点：①几何模型是精确的，避免了几何模型误差，提高计算精度；②几何模型是由控制点决定的，避免了网格再划分的工作，提高了计算效率。此外，在用于模型形状优化分析的敏感度求解方面也具有一些优势：①对具有高阶效应的复杂几何模型的敏感度分析更精确。NURBS基函数具有高阶连续特性，比拉格朗日形函数包含更多的信息，更有利于进行结构响应分析和敏感度计算；②在基于敏感度分析的优化过程中，大大简化了修改模型与原CAD模型几何数据的交互，由于NURBS基函数的使用，仅需简单地移动等几何节点位置，即可实现分析模型的形状优化[5]。因此，IGA方法的建立，使复杂实际结构的形状拓扑优化得以有效开展。

边界元法已广泛应用于流体力学、声学、电磁学、断裂力学等工程领域。与其他数值方法相比，边界元法(Boundary Element Method，BEM)在求解无限域或半无限域问题上，具有独特的优势。近些年，一些学者将IGA与BEM结合起来，发展了等几何边界元法(IGABEM)，并有效应用于位势问题和弹性力学领域。例如，Gu等[6]将IGA与边界面法相结合，进行三维位势问题分析；Gong等[7]将该方法应用到三维位势问题领域；Simpson等[8]详细给出了该方法的计算流程，并应用到二维弹性力学领域。近几年，IGABEM开始被应用到声学领域。例如，Peake等[9]采用该方法进行二维Helmholtz问题分析，随后，Coox等[10-11]对该方法进行深入研究，从二维到三维，从NURBS样条到T样条。另外，Kostas等[12]采用IGABEM进行弹性力学问题的敏感度计算和形状优化分析，这些研究都显示出IGA在形状优化中具有巨大的优势。然而，在声学领域的敏感度分析及其结构声学优化分析却研究较少。对于本文所关心的外声场问题，采用IGABEM可自动满足无限域处的索莫菲边界条件，只需对结构外表面进行离散和数值积分计算；单元上的积分面和变量都采用NURBS基函数插值得到，但是NURBS基函数是通过递推公式计算得到的，在边界元系数矩阵元素计算过程中，需要增加一次循环计算，这会降低IGABEM的计算效率，导致相同自由度数的IGABEM比传统BEM消耗更多的计算时间，但由于结构模型的精确建立也产生更高精度的计算结果。另外对于带有很多间断不光滑结构面的描述，基于NURBS的IGA方法还是很难实现的，因此限制了该方法对于实际复杂问题的应用。但一些方法可以用来改善这一缺点，例如T样条插值、细分曲面等。虽然IGA有这些难以克服的缺点，但由于其在结构形状表征和形状优化上的独特优势，国内外很多学者致力于该方法的开发和应用研究上。

本文采用IGABEM进行声学敏感度分析，使用Burton-Miller方法克服外声场的非唯一解的问题[13-14]，并推导出无奇异敏感度边界积分方程。然后以等几何控制点坐标作为设计变量，以声屏障降噪区域的声压作为目标函数，以结构的面积大小作为约束，建立二维声屏障结构声学优化数学模型，并采用MMA(Moving Approximation Algorithm)方法进行寻优计算。

1 基于边界元法的二维声学状态分析

1.1 基于传统边界元法的二维声学状态分析

对于半空间二维声学问题，传统边界积分方程(Conventional Boundary Integral Equation，CBIE)和法向导数边界积分方程(Normal Derivative Boundary Integral Equation，NDBIE)分别表示为

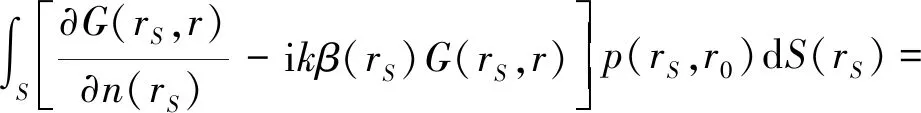
(1)

(2)

式中：r0为声源点；β为声导纳。格林函数为

(3)

将CBIE方程和NDBIE方程线性组合后形成的Burton-Miller方程可以有效的克服数值解的非唯一性问题。将边界S离散后，可得到如下的线性代数方程组

[H-ikGB]P=Pi

(4)

(5)

式中：H和G为边界元系数矩阵；P为节点声压向量；Pi为入射声压向量；βi为结构表面第i个边界单元上的吸声材料介质导纳参数。

实际上，式(1)和式(2)的积分计算需要克服奇异性问题。Sx代表包含源点r的边界单元，在该边界单元上的积分具有奇异性，需要做出特别处理。在这里，柯西主值积分和Hadamard有限部分积分法被用于克服这一问题。 在Sx上的两项奇异积分分别为

(6)

(7)

式中：ξ为每个单元的局部坐标；J为雅可比。

(8)

(9)

式中：m为边界元内插值节点的个数； 当拉格朗日函数插值用于数值解时，pi为单元节点声压向量。而对于NURBS基函数，则表示在对应的控制点上的声压值。将式(8)代入式(9)，我们可以得到

(10)

使用不同类型的拉格朗日函数进行边界元积分计算，可得到Bi和Di的不同表达。当使用NURBS基函数进行边界元插值计算时，需作出不同处理。首先，NURBS基函数为

(11)

(12)

(13)

(14)

然而， 对于p=1,2,3。

(15)

将式(11)代入式(10)， 可得到基于NURBS插值计算的Bi和Di的表达式为

(16)

(17)

在精确得到奇异积分的计算表达式后，亦是给出系数Bi和Di的表达式，进而可以得到无奇异的边界积分方程式(6)和式(7)。最后使用式(4)可得到节点处未知变量值。

1.2 基于传统边界元法的二维声学形状灵敏度分析

将式(1)和式(2)分别对设计变量进行求导，可得

(18)

(19)

(20)

(21)

式(20)和式(21)等号右边第二项是非奇异的，可以用高斯积分法求解。然而，右边的第一项是奇异性的。通过使用式(9)，我们可以得到以下表达式

(22)

(23)

当使用NURBS基函数进行数值计算时，边界曲线可表示为

(24)

式中：X(ξ)为边界点的坐标；n为控制点数量；Pi为控制点的坐标。将式(24)对设计变量进行求导，可得如下边界曲线敏感度表达式

(25)

同样地，可得到坐标导数的敏感度表达式边界积分解

(26)

结合式(18)和式(19)，消除奇异边界积分后，最终可以得到如下敏感度边界积分方程

(27)

利用上述方程，我们可以得到用于物理场近似的特殊控制点处的声压敏感度值。然后利用式(18)得到域内任意点处的声压敏感度pf。

2 声学结构形状优化模型的建立

对于结构声学形状优化问题，等几何控制点决定结构形状及几何尺寸，将其选做优化设计变量，能灵活的体现形状的变化。选取参考区内若干点上的声压作为目标函数。在二维声学结构形状优化中，结构面积是重要的约束条件，以声影区参考点声压幅值在一定频带上的均值为目标函数，满足多约束条件下的目标函数最小为设计目标，优化过程中采用MMA法更新设计变量[15-17]。综上所述，该优化问题的数学模型可表示为

(28)

目标函数∏(X)对形状设计变量x的灵敏度表示为

(29)

式中： R为取复数的实部值。 当采用基于梯度分析的MMA方法进行优化分析时， 约束函数A0(封闭结构的面积)的求解是非常重要的，因此结构的面积可由边界积分计算出，表达式为

(30)

另外结构面积对设计变量的敏感度为

(31)

式中：Ne为NURBS单元数； [ξe,ξe+1]为第e个NURBS单元在参数空间内的位置。

3 直立型声屏障的形状优化

3.1 直立型声屏障模型描述

图1 直立型声屏障初始模型Fig.1 Initial model of vertical shape sound barrier

利用NURBS建模的初始控制点为图中6个点，坐标分别为p0=(5.2,0)，p1=(5.2,3)，p2=(5.2,3)，p3=(5,3)，p4=(5,3)，p5=(5,0)。 对应的节点向量为Ξ=[0.0,0.0,0.0,0.45,0.45,0.55,0.55,1.0,1.0,1.0]， 阶数pg=2。

3.2 单频激励下优化结果

本节研究了声屏障在单频激励下的形状优化。需要注意的是，选择适当的控制点数量对于基于IGA的形状优化分析是十分必要的。更多的控制点数可以生成更灵活更复杂的的结构外形，自然可得到更低目标函数值，但设计变量的增加往往大大提高CPU(Central Processing Unit)计算时间，因此找到合适的优化控制点数是很有必要的。在图2中，纵坐标表示目标函数值，横坐标表示MMA迭代次数，4个不同控制点数被用于优化分析。起初随着MMA迭代次数的增加，不同设计变量数目的曲线都会快速收敛到一个固定值，同时随着控制点数N由5～20的增加，目标函数最终收敛值也在逐一下降表明随着控制点数的增加，优化自由度在不断提高，可得到更好的降噪效果。与此同时，需要更多的CPU时间，并且此时目标函数随N增加时下降速率逐渐变缓，表明随着N的增加，每增加一个控制点目标函数值降低的幅度是越来越小的。这说明当优化自由度增加到一定程度后，再增加设计变量数目降噪效果是不会有太大提高的。图3显示了不同优化控制点数目下面积约束收敛的效果，设计变量数目越多，最终面积的利用率就越大。图4表示计算频率400 Hz时优化控制点数目越多，优化后声屏障的形状就越复杂，降噪效果也越显著。从图5中可看出，当控制点数目相同计算频率不同时优化结果并不相同，计算频率越大优化后的结构形状越复杂，说明单频优化结果具有很强的频率依赖性，因此需要进一步在整个频带上进行形状优化研究。在图6中，横坐标表示目标区域内参考点的编号，纵坐标表示声压级值。Initial value表示声屏障初始形状时目标区域内参考点的声压级值，Optimal value表示声屏障形状优化后参考点的声压级值。声压级值与声压值的关系为

图2 400 Hz时不同优化控制点数目下目标函数随迭代次数变化Fig.2 Objective function in terms of iteration step for different numbers of design variables

图3 400 Hz时不同优化控制点数目下面积约束随迭代次数变化Fig.3 Area constraint in terms of iteration step for different numbers of design variables

(32)

式中：φ0为参考声压，空气中参考声压取2×10-5Pa。从图6中可以看出声屏障形状在优化后声压级值明显降低，表明降噪效果有了很大的改善。与此同时优化结果对频率的依赖性依然较强。通过对不同频率下声屏障形状的优化，声压级值降低的幅度也是不同的。如频率400 Hz时降噪改善在5 dB，频率700 Hz时降噪改善达到8 dB等。从声源波长的角度分析，声源频率越高，波长就越短，进而波长与声屏障的零碎尺寸比值就越小，从而越不容易发生衍射，表明声屏障对高频声源的降噪效果更具敏感性。

图4 400 Hz 时不同优化控制点数目下声屏障最终优化形状Fig.4 The optimized shape of the sound barrier with different numbers of optimization control points

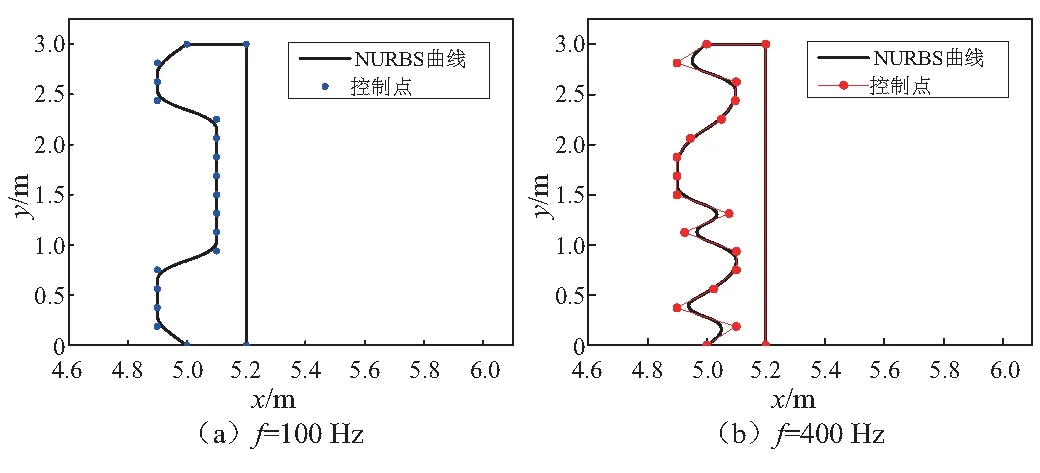
图5 不同频率下声屏障最终优化形状Fig.5 The final shape of the sound barrier with 15 control points at different frequencies

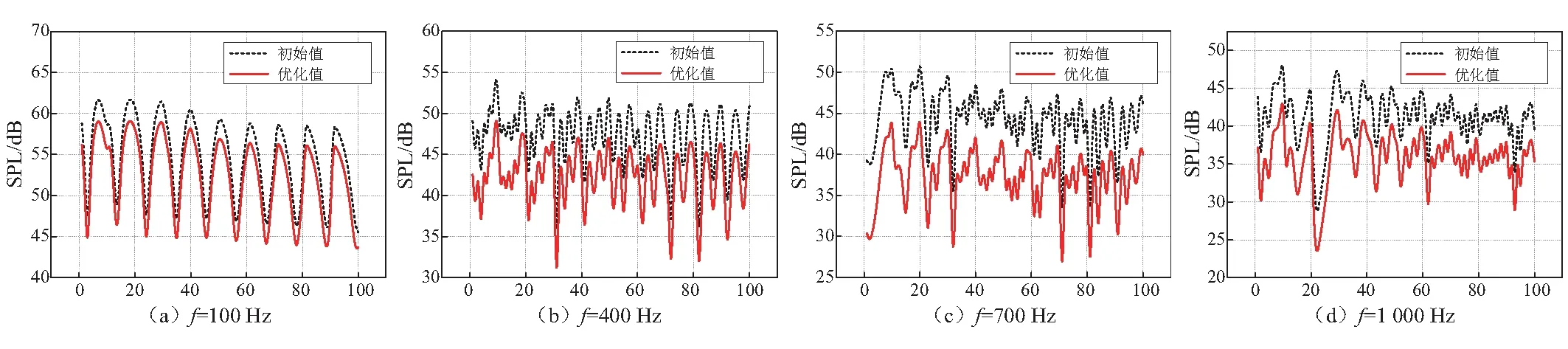
图6 优化前后不同频率下参考区内计算点处声压级变化Fig.6 Improvement of noise reduction at different frequencies

总之，基于IGABEM方法的形状优化分析，选取一定数量的形状控制点为设计变量，数量越多，优化后的形状就越复杂，虽然可得到更优的计算结果，但由于设计变量数量的增加，也消耗了更多的计算时间，因此，选取一个合适的设计变量数是重要的。经验上，在计算量可以接受的情况下，尽可能在边界线或面上布置更多的优化控制点。下一步，我们会进一步考察优化控制点数与计算量之间的对应关系，给出经验表达式。另外，优化控制点数的增加，还导致优化过程中的收敛迭代步数大大增加，大幅降低优化算法的计算效率，下一步，通过发展有效的预处理方法和迭代求解算法，提高优化算法的计算效率。

3.3 频带激励下优化结果

由于现实生活中声源的频率是复杂的，并不是以单频存在，通常分布在某一个特定的频率带内。为此需要在一个频率范围内建立一个平均目标函数，频带内的目标函数为

(33)

式中：ω1为下限频率；ω2为上限频率； ∏为单频下的目标函数，可参见式(28)。频带内目标函数敏感度表示为

(34)

图7 200～500 Hz频带内声屏障最终优化形状Fig.7 The final shape of the sound barrier in certain frequency band

另外，得到的优化声屏障结构外形由于表面凸凹不定，复杂多变，是难以直接应用于实际工程问题，实际上可通过增加约束条件达到符合实际规范的优化结构外形，这也是我们接下来的重点工作。本文的重点是进行基于等几何的结构声学优化设计算法研究，使用声屏障结构主要是为了验证开发算法的有效性。

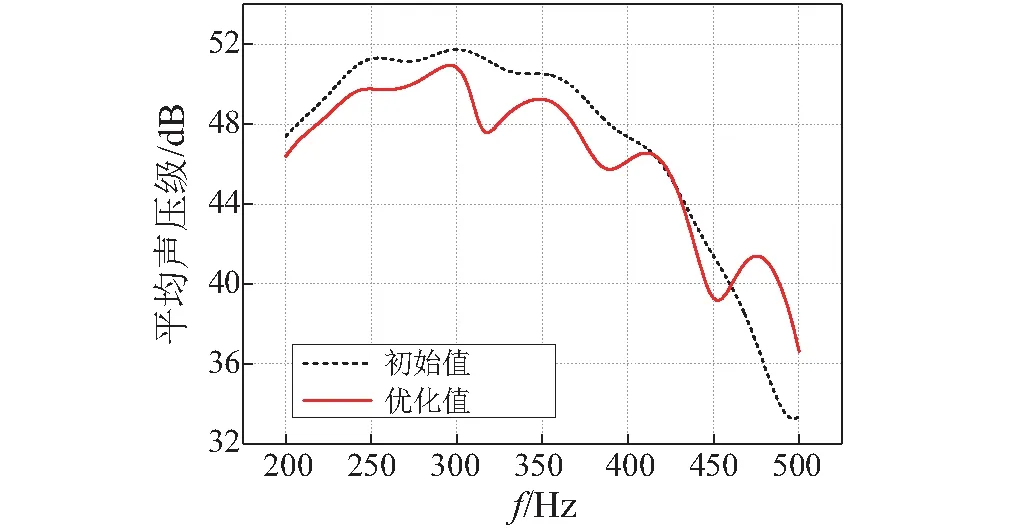
图8 不同频带下声屏障优化后降噪效果Fig.8 Noise reduction effect after noise barrier optimization in terms of frequencies

4 结 论

本文主要介绍了二维声场等几何边界元的声学状态分析、声学形状敏感度分析及建立结构形状优化模型，导出了带有设计变量的目标函数灵敏度分析表达式，并通过实例验证了基于等几何边界元法的声学结构形状优化算法，结果表明优化后的结构形状对降噪效果确有改善，同时声学结构的形状优化与频率是密切相关的，在不同的计算频率下最优解不同，即降噪效果不同。如与实际相结合，通常考察一定频带内的优化结果往往更加有效。该方法的突出特点是将设计变量作为等几何建模的控制点，采用MMA方法更新优化过程中的设计变量，灵活准确地控制形状变化，并通过敏感度分析找到形状变化与声场声压分布的对应关系，从而解决最优解问题。