变刚度转臂定位节点对地铁车辆车轮磨耗的影响

2019-04-03祁亚运戴焕云

振动与冲击 2019年6期

祁亚运，戴焕云，魏来，干锋，徐坤

(西南交通大学牵引动力国家重点实验室，成都 610031)

随着我国轨道交通的迅速发展，地铁运营里程逐年增加。载客量不断增大，地铁车轮磨耗问题日益显著。地铁线路一个重要特点是小曲线多，车辆启动制动频繁。因此地铁车轮存在严重的磨耗，钢轨也出现大量的波磨现象。关于地铁车轮磨耗的问题，国内为学者十分关注这一问题。首先Pearce等[1-3]根据试验提出了车轮磨耗模型，并确定了相关系数。Han等[4]根据实测车轮磨耗型面的拟合出了车轮磨耗模型并用于车轮磨耗预测取得了不错的效果。Pombo等[5]利用多体动力学软件仿真并用于车轮磨耗预测。Ignesti等[6]采用磨耗模型分析了钢轨和车轮的磨耗。陶功权等[7]在考虑稳定性的基础上进行车轮磨耗预测。罗仁等[8-9]探究了不同的系统参数对车轮磨耗的影响。于春广等[10]对地铁车轮磨耗进行了跟踪测试，提出相应车轮减磨措施。陶功权等[11]从静力学角度分析了不同轨底坡对我国常用于地铁车辆的LM, 51002和DIN5573型面与CN60钢轨匹配的轮轨接触特性的影响。沈钢等[12]对比初始与实测轮轨型面对上海地铁A型车的曲线通过性能的影响，并分析不同的轮轨型面匹配对轮轨磨耗、钢轨波浪形磨耗、接触疲劳的影响。李霞等[13]介绍了车轮磨耗的预测方法。考虑轮轨动态接触状态，采用数值分析方法分析异常磨耗的地铁车轮和新钢轨作用情况，且对导致地铁车轮踏而异常磨耗的原因作了分析。丁军君等[14]在SIMPACK软件中建立地铁车辆动力学模型，基于FASTSIM算法和Braghin踏而磨耗模型，分析弹性滑动速度对磨耗的影响，并对车辆在直线、曲线和实际线路上运行时的车轮磨耗过程进行仿真。张隶新等[15]利用变刚度转臂定位节点对车辆动力学的影响。孙宇等[16]研究了凹形磨耗下轮轨两点接触时的轮轨力和动力学性能。李国栋等[17]研究了LMB踏面长期磨耗状况下其动力学性能和轮轨接触关系的研究，最后表明LMB踏面延长了车轮磨耗里程，同时在磨耗周期内减弱了车辆振动。杨阳等[18]通过结合机车动力学仿真和Achard磨耗模型研究了不同牵引力矩对车轮磨耗的影响，同时与实测踏面数据进行对比。李亨利[19]主要研究了货车车轮磨耗的规律和不同的影响因素。杨新文等[20]采用修正的非Hertz接触算法计算了曲线超高对钢轨磨耗的影响。

本文首先分析了变刚度转臂定位节点模型的频变特性和幅变特性，利用该模型的在曲线通过时的优势，将其用于地铁转臂定位节点的磨耗仿真分析，计算了定刚度和变刚度转臂定位节点在曲线通过时的受力。最后采用Zobory模型计算了地铁车辆的通过不同线路状况的磨耗深度，并进行了车轮磨耗预测分析以及模型参数对磨耗的影响。

1 模型建立

1.1 转臂定位节点建模

转臂定位节点是连接构架和轴箱机构的重要部件，一般是橡胶件。转臂定位装置如图1所示。德国Freudenberg Schwab公司开发了具有变刚度特性的转臂定位节点，变刚度转臂定位节点模型考虑了其频变特性，在直线上刚度大，表现为硬特性；在曲线上刚度较小，表现为软特性，具有自适应的调节功能，改善了车辆的曲线通过性能。本节采用Poynting-Thomson模型(以下简称PT模型)模拟该变刚度定位节点的非线性特性。PT模型如图2所示。其中包括2个弹簧单元和1个阻尼单元，弹簧与阻尼组成串联单元，该串联模型再和弹簧并联组成PT模型。

图1 转臂定位节点装置Fig.1 Rotary arm positioning node device

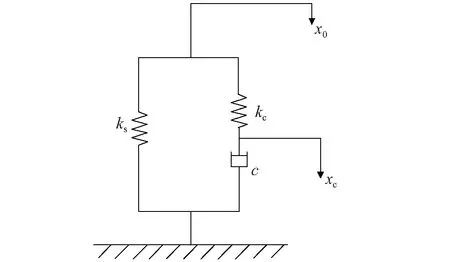
图2 Poynting-Thomson模型示意图Fig.2 Poynting-Thomson model schematic diagram

在PT模型中，x0=A0·sin(2πf·t)。其中：A0为激扰幅值；f为激扰频率。串联单元的力F可以表示为

F=ksx0+kc(x0-xc)

(1)

PT模型中的具体参数见表1。从式(1)可知， PT模型中力与位移的关系，通过改变激扰频率和激扰幅值，可获得系统的非线性刚度和阻尼特性曲线。

表1 模型参数

图3和图4给出了PT模型的频变特性和幅变特性曲线，从图3可知，频率增大后，示功图斜率越大，说明刚度变大，示功图面积变小，说明模型阻尼变小。从图4可知，随着幅值的改变，频率不变，因此刚度不会增大。随着幅值增大，示功图增大，模型阻尼也增大。

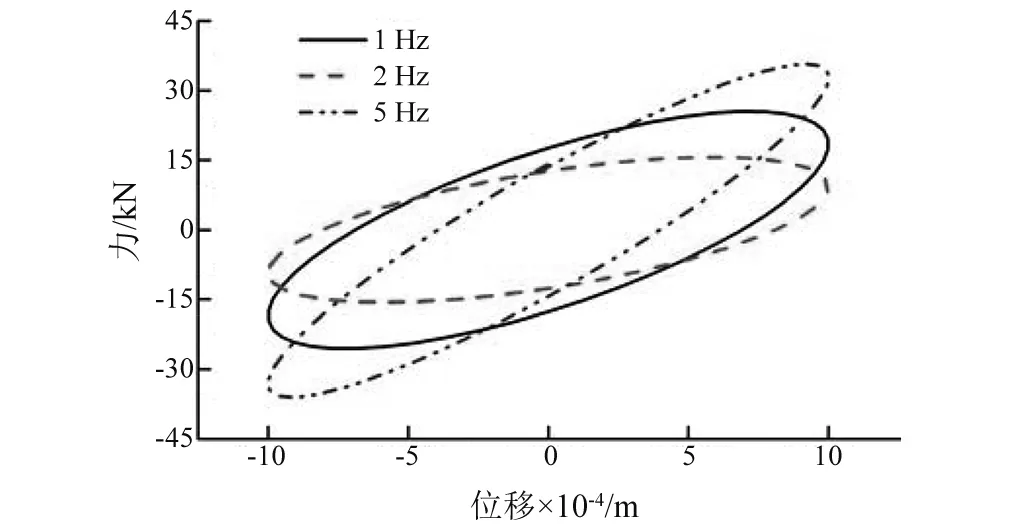
图3 模型频变特性Fig.3 The frequency variation characteristics of model

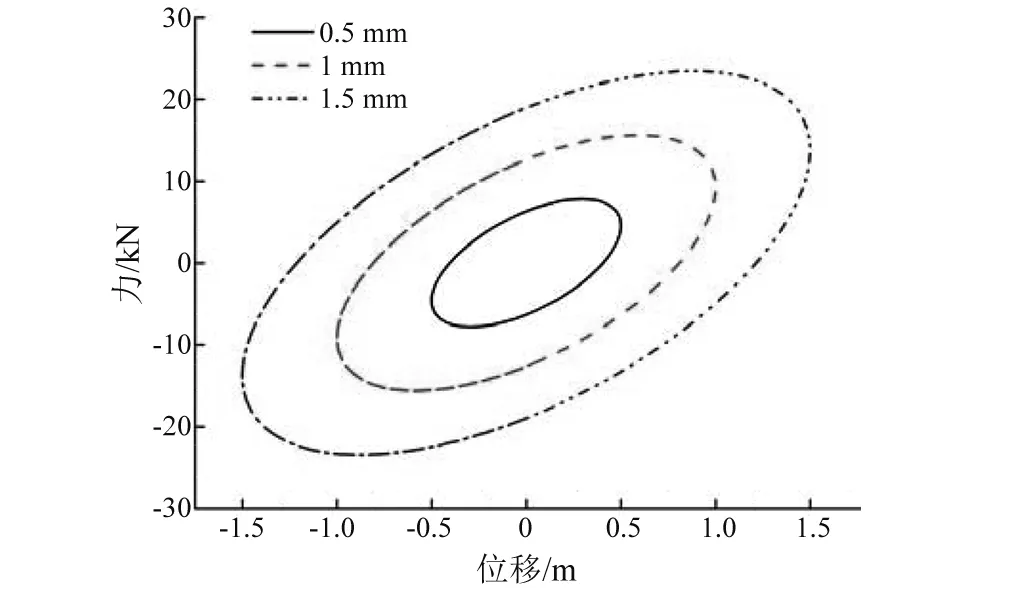
图4 模型幅变特性Fig.4 The amplitude variation characteristics of model

仿真值和试验刚度对比，如图5所示。从图5可知，试验值和理论值有很好的一致性。模型准确地模拟了频变刚度特性。因此将该模型用于变刚度转臂节点仿真时有效的。

图5 仿真计算和试验刚度试验值对比Fig.5 Comparison of simulation and test stiffness test values

1.2 车辆模型

建立我国地铁车辆模型，采用LM踏面，选取1个车体，2个构架、4个轮对与8个转臂以及一系悬挂和二系悬挂系统组成车辆系统。车体、构架、轮对考虑了纵向、横向、垂向、侧滚、点头、摇头6个自由度。轮对的垂向和侧滚运动耦合在一起；转臂只考虑点头自由度，该模型考虑车辆自由度，如表2所示。以车辆前进方向为x轴，y轴为平行于轨道方向，z轴为垂直于轨道向下建立坐标系。车辆模型如图6所示。考虑轮轨非线性的接触关系和车辆悬挂系统，车辆系统的动力学方程表示为

(2)

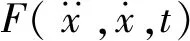
表2 车辆自由度

图6 车辆动力学模型Fig.6 Vehicle dynamics model

1.3 轮轨接触算法

计算轮轨接触特性时，选用Hertz-FASTSIM的的快速算法，即轮轨间法向力的计算采用Hertz接触理论，切向接触应用FASTSIM接触理论。这种算法由Hertz接触理论计算椭圆接触斑大小，并在接触斑内划分网格单元，每个单元的长度为Δi和Δj。接触单元上的法向力为

(3)

(4)

式中：pz(i,j)为接触网格上的法向力分布；a，b为接触斑长轴、短轴一半； Δv，Δvi，Δvj为相对滑动速度、纵向相对滑动速度、横向相对滑动速度；vi为质点通过接触点的速度。

并假设接触斑内任意一点(i,j)的弹性位移u与同方向的法向力p和柔度系数L有关，即：u(i,j)=L·p(i,j)，滑动方程描述为

(5)

式中：Vi，Vj为纵向和横向滑动速度；Vv为列车运行速度；ξi，ξj为纵向和横向蠕滑率；φ为自旋蠕滑率；u1，u2为纵向和横向弹性位移。

弹性滑动速度可以表示为

(6)

黏着区和滑动区共同构成了接触斑区域，磨耗主要发生在接触斑内的滑动区。将接触区进行划分(见图7)，假设切向力的大小与轮轨间的切向应变成线性关系。

u(i,j)=L·F(i,j)

(7)

式中：u(i,j)为弹性变形；L为柔度系数；F(i,j)为轮轨间的切向力。柔度系数L可以利用KALKER理论中蠕滑力与蠕滑率之间的关系得到。

(8)

图7 椭圆接触斑示意图Fig.7 Sketch of ellipse contact spot

接触斑(长轴是2a，短轴长为2b)被划分成i×j个接触单元，单元格的长度分别为Δi和Δj，见图2。任意单元内，滑动速度与刚性滑动量和切向变形有关，即

(9)

式中：vs(i,j)滑动速度；p(i,j)为刚性滑动量。

(10)

在黏着区域，滑动速度为0，左边为0，切向力为

(11)

在滑动区域，根据库伦摩擦定理：当接触斑单元上的切向力大于其最大摩擦力(轮轨法向力乘以摩擦因数)，若F(i,j)≤Fmax(i,j)，则单元格处于黏着区；若F(i,j)>Fmax(i,j)，则滑动出现，滑动区单元格切向力

(12)

1.4 ZOBORY磨耗模型

在ZOBORY磨耗模型中，接触斑划分为nx×ny个单元格，由上节可知，轮轨接触区划分为黏着区和滑动区，分别表示为Aa和As。根据轮轨蠕滑理论，黏着区内不发生磨耗，只在滑动区发生磨耗。接触斑内的磨耗能量流密度为

(13)

(14)

应用质量流密度计算单位面积的质量为

(15)

图8 磨耗系数Fig.8 Coefficient of wear

由于接触班划分的网格块很小，可以近似为

(16)

则磨耗深度可以表示为

Δz=Δm/(ρ·ΔA)

(17)

式中： Δz为磨耗深度；ρ为材料密度；将式(15)代入式(17)就可以计算出接触班上网格块的磨耗深度。

2 变刚度模型动力学性能

2.1 变刚度模型曲线通过性能

为了计算变刚度模型曲线通过性能，采用500 m曲线半径，超高为120 mm，速度为70 km/h。轨道激扰采用地铁线路轨道激扰。分别计算了变刚度模型和定刚度模型的磨耗功、轮对冲角以及纵/横向蠕滑力。

从图9～图11中可知，车轮通过500 m曲线时的车轮磨耗功、轮对冲角和蠕滑力计算结果，从图中可以看出采用变刚度模型时的磨耗功比定刚度模型减小50%。采用变刚度模型时轮对冲角比定刚度模型减小55%，因此可以看出采用变刚度模型时曲线通过性能有了很大提升，而且减小了车辆通过曲线的磨耗；定刚度模型纵向蠕滑力最大值为13 kN，动刚度模型的纵向蠕滑力为5.5 kN。定刚度模型的横向蠕滑力值为10 kN，变刚度模型的横向蠕滑力为6 kN。变刚度模型使得纵向蠕滑力和横向蠕滑力明显降低。

图9 磨耗功Fig.9 Wear power

图10 轮对冲角Fig.10 Wheelset angel

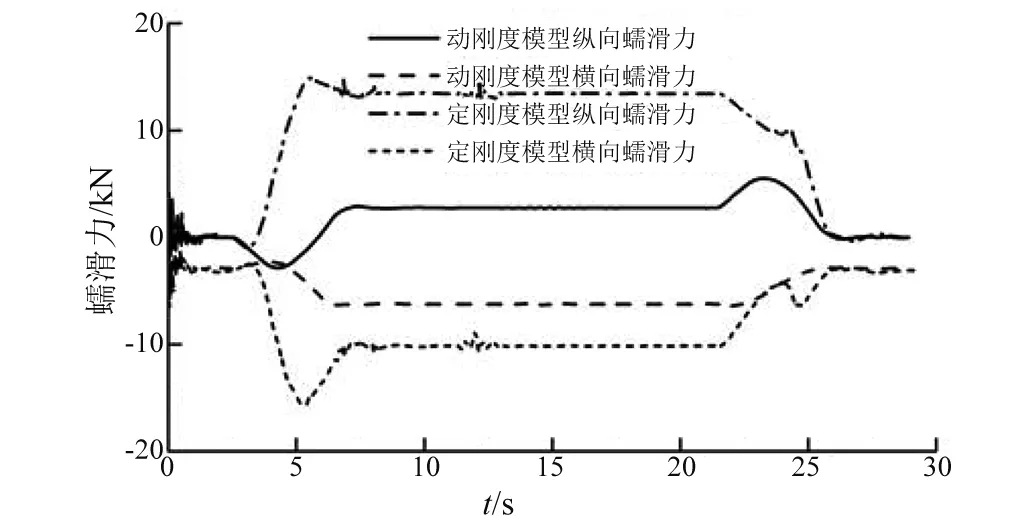
图11 蠕滑力Fig.11 Creep force

2.2 变刚度模型平稳性和安全性计算

由上节可知，采用变刚度节点具有较好的曲线通过性能，但对于车辆的平稳性和安全性影响未知，本介计算了两种模型下平稳性和安全性指标。

从图12可知，采用动刚度模型时车体中部平稳性有所降低，当速度在100 km/h时，平稳性指标降低5.6%。从表3可知，采用动刚度模型时其轮轨横向力和倾覆系数和定刚度模型差别较小，脱轨系数和轮重减载率都有了一定的减小，脱轨系数较小了10.2%，轮重减载率减小了9.3%。

图12 车体中部平稳性指标对比Fig.12 Comparison of ride index in the middle of car body

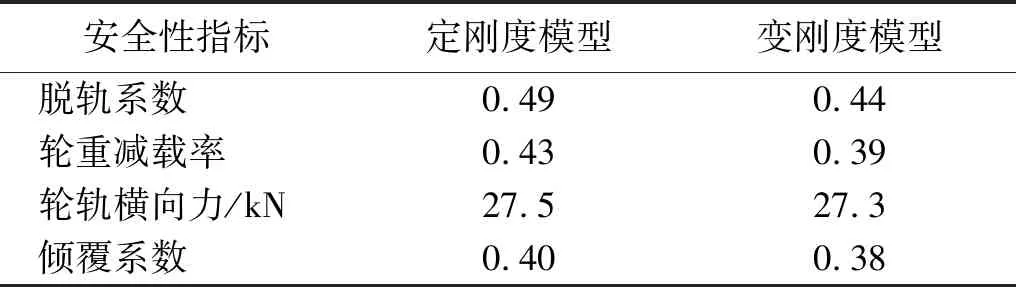
安全性指标定刚度模型变刚度模型脱轨系数0.490.44轮重减载率0.430.39轮轨横向力/kN27.527.3倾覆系数0.400.38

因此采用变刚度模型的平稳性性能有所降低，其安全性指标在曲线上比较关注的脱轨系数和轮动减载率都有所降低。

3 车轮磨耗仿真分析

车轮磨耗预测主要包括以下步骤：

步骤1车辆动力学仿真，通过SIMPACK建立车辆动力学模型，计算出每一积分步的轮轨接触参数，并将轮轨接触参数输出。

步骤2局部轮轨接触计算，采用Karlker算法重新划分接触斑网格，区分黏着区和滑动区，计算磨耗模型需要的参数。

步骤3车轮磨耗计算，计算接触斑磨耗深度并线性插值累加到踏面上，并将累加后的磨耗深度进行平滑。

步骤4踏面更新。

其计算流程如图13所示。

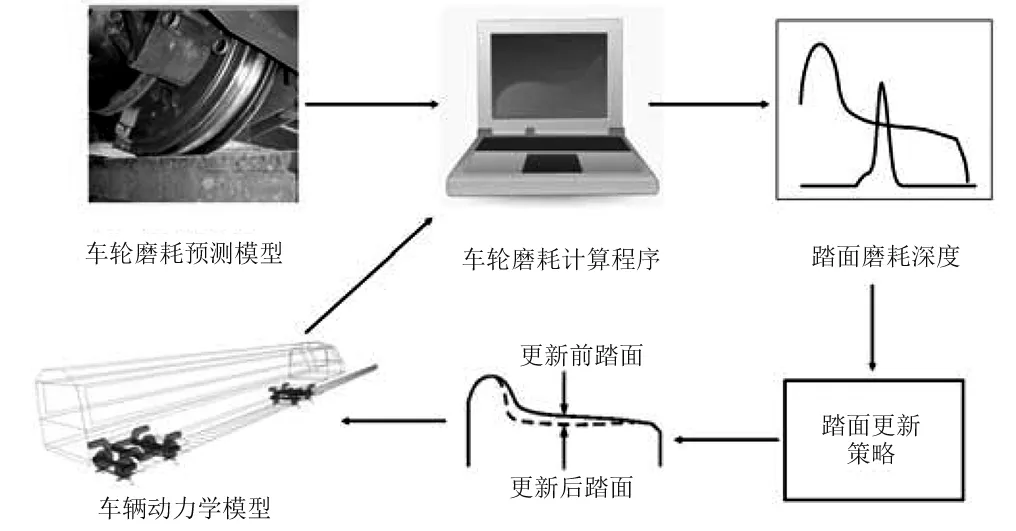
图13 车轮踏面磨耗计算过程示意图Fig.13 Diagram of wheel tread wear calculation process

3.1 直线工况下车轮磨耗

仿真踏面为LM踏面，轨面为60轨。轨底坡为1∶40。在600 m直线上两种模型的车轮磨耗深度，采用实测线路轨道激扰。磨耗深度计算采用zobory模型，图14给出了两种模型在直线工况下的车轮磨耗深度值，当采用定刚度模型时车轮磨耗深度相对于定刚度模型明显减小，1位轮对左轮磨耗深度减小55%,1位轮对右轮磨耗深度减小46%。因此在直线工况下变刚度模型能够有效降低车轮磨耗。

3.2 曲线工况下车轮磨耗

仿真选用实测轨道谱，曲线半径为500 m，缓和曲线长100 m，圆曲线长200 m，超高为120 mm，轨底坡为1∶40。采用Zobory模型计算了左右车轮磨耗深度。从图15可知，当采用定刚度模型时，1位轮对左车轮磨耗深度为70×10-9m；当采用变刚度模型时，1位轮对右车轮磨耗深度为19×10-9m，且磨耗更均匀，车轮最大磨耗深度减小72.8%。当采用定刚度模型时，1位轮对右车轮磨耗深度为55×10-9m，采用变刚度模型时，1位轮对右车轮磨耗深度为18×10-9m，车轮最大磨耗深度减小67.3%。因此，从磨耗深度的仿真结果来看，变刚度模型有效地降低了地铁车辆通过曲线时的车轮磨耗。

图16给出了不同曲线半径下，计算了基于定刚度模型和变刚度模型车轮磨耗深度。随着曲线半径的增大，定刚度模型和变刚度模型车轮磨耗深度都不断降低，两种模型的磨耗深度之差逐渐减小。可见，曲线半径越小，变刚度模型的在减缓磨耗方面作用更加显著。在300 m，500 m，800 m和1 000 m曲线半径下，变刚度模型磨耗深度均小于定刚度模型磨耗深度。

图14 直线工况下车轮磨耗深度Fig.14 Wheel wear depth under a straight line

图15 曲线工况下车轮磨耗深度Fig.15 Wheel wear depth under a curve line

图16 不同曲线下的磨耗深度Fig.16 Wheel wear depth under diffrent curve lines

3.3 长距离车轮磨耗预测

由于缺乏买际线路货料，因此本文选用表4所示的线路。为了减少计算量，本文做了以下假设：①线路上左曲线和右曲线对称分布；②列车不掉头往返运行；③每条曲线或直线的摩擦因数均为3；④计算中不考虑钢轨型面的磨损。基于以上假设，车辆第1，第4轮对左右车轮的磨耗相同，第2，第3位轮对左右车轮的磨耗也相同，在计算时给出第1位轮对车轮的磨耗仿真结果。

表4 线路设置参数

采用以上线路工况，现分别就就两种模型进行5万km里程的磨耗预测，给出了车轮磨耗后型面和车辆磨耗深度，如图17所示。

图17 5万km车轮磨耗预测Fig.17 Wheel wear prediction of 50 thousand km

由图17可知，定刚度模型车轮的磨耗分布主要出现在车轮名义滚动圆士40 mm范围内，变刚度模型车轮的磨耗分布主要出现在车轮名义滚动圆士20 mm范围内。在运行里程为5万km的情况下，采用定刚度模型的最大磨耗深度为0.9 mm，出现的位置在名义滚动圆外侧10 mm处，同时在名义滚动圆内侧30 mm处磨耗也较大，这是由于过曲线时轮缘根部频繁接触造成的，采用变刚度模型时最大磨耗深度均出现车轮名义滚动圆内侧约5 mm处，最大磨耗深度为0.52 mm。最大磨耗深度减小42.2%。可以看出长距离运营工况下，采用变刚度模型可以有效减小车轮磨耗深度，改变车轮磨耗范围。

地铁车辆在实际线路中运行环境复杂，线路情况复杂，而仿真计算中仅采用了几条典型的线路工况，仿真中轮轨材料的塑性流动、天气因素对轮轨界面摩擦因数的影响均未在考虑范围内。因此仿真计算结果与车轮实际磨耗可能存在一定的差异。但本文仿真作为理论分析，只作定性研究。

3.4 参数对车轮磨耗的影响

图18中给出了串联刚度、并联刚度、并联阻尼系数对车轮磨耗的影响，从18(a)可知，随着串联刚度的增大，车轮磨耗深度不断增大，当从20 MN增大到40 MN时，车轮磨耗深度增大55%，从40 MN增大到60 MN时，车轮磨耗深度增大45.1%。从图18(b)和图18(c)可知，并联刚度和串联阻尼系数对车轮磨耗的影响较小，当并联刚度从4 MN增大到8 MN时，车轮磨耗深度从31×10-9增大到了33×10-9，增大了6.41%，当串联阻尼系数从0.2 MN增大到1 MN时，车轮磨耗深度增大2.4%。因此，串联刚度对变刚度模型的车轮磨耗影响最大。并联刚度和串联刚度阻尼系数对对定刚度模型的车轮磨耗影响较小。