BIF型磁铁矿石冲击破碎特性的能量效应

2019-04-03甘德清刘志义张成龙

振动与冲击 2019年6期

甘德清，高锋，刘志义，张成龙

(1. 华北理工大学矿业工程学院，河北唐山 063210； 2. 河北省矿业开发与安全技术重点实验室，河北唐山 063210；3. 首钢集团有限公司矿业公司水厂铁矿，河北迁安 064400)

条带硅铁建造(BIF型)磁铁矿石是我国铁矿企业的主要产品，也是我国钢铁行业的主要原材料，品位主要为20%～40%，需破碎加工成精矿后才能用于冶炼。冲击破碎是磁铁矿石的主要破碎方式，能量是驱动矿石破碎的根本原因，直接影响破碎质量。我国磁铁矿石破碎加工规模巨大，单位能量消耗过高。因此，为了弄清能量对磁铁矿石破碎的本质作用，进而解决磁铁矿石破碎能量消耗过高的问题，有必要研究能量对BIF型磁铁矿石破碎特性的影响关系。

目前，国内外许多学者研究了矿岩石冲击破碎的能量特征及其对破碎结果的影响关系。Saeidi等[1]进行了单颗粒多次冲击破碎试验，分析多次冲击破碎过程的能量变化特征和能量对逐次破碎结果的影响。Narayanan等[2]采用t10(筛孔直径为初始粒径1/10时的筛下质量分数)研究冲击破碎效果，分析能量与破碎粒度的关系，并将试验结果用于球磨机参数优化。Tavares等[3]进行了单颗粒一次冲击破碎试验，分析了破碎颗粒的数量和能量的关系。Sadrai等[4]使用高孔隙率石灰岩、石英岩和岩盐进行空气炮高速冲击破碎试验，得出了能量效率的计算方法和适用范围。张文清等[5-7]通过霍普金森冲击破碎试验探究了冲击破碎的能量转化关系，分析了破碎能量与破碎粒度分布之间的相关关系。牛雷雷等[8]研制了适合中应变率冲击加载的摆锤压杆冲击试验装置，测试了矿岩破碎的吸收能，得到破碎能量与破碎结果的理论关系。部分学者开展了轻气炮霍普金森冲击试验，研究矿岩石冲击破碎能量与破碎结果的量化关系，得到能量与破碎程度指标的关系模型[9-11]。胡振中等[12]对淮北无烟煤和烟煤进行单块矿石落锤冲击破碎试验，以产物粒度模数t10为破碎粒度指标，得出比冲击能耗随产物t10的增大指数增长。Napier-munn等[13-14]分别通过落锤和摆锤冲击试验研究提出了单颗粒冲击能耗模型，指出冲击破碎能量与产品粒度模数之间的函数关系，并进行了很好的验证。Wu等[15]使用不同尺寸不同强度的石膏球进行冲击速度为1～9 m/s的两次落锤破碎试验，得到小颗粒碎屑数量与冲击能成正比。Reddish等[16]通过室内落锤冲击试验和Flac数值模拟试验研究了冲击能对圆柱形花岗岩试件破碎程度的影响。

以上研究侧重于岩石破碎能耗对破碎结果的影响，在落锤冲击试验研究中缺乏能量转化与效率特征的讨论，对落锤冲击作用下能量对BIF型磁铁矿石破碎特性和产品粒度分形的影响关系研究较少。矿石加工过程中，机械与矿石之间发生挤压或接触撞击作用实现矿石破碎。为接近矿石破碎的实际情况，采用导杆式落锤冲击试验系统，通过室内试验研究落锤直接冲击破碎BIF型磁铁矿石的能量与分形特性，探讨落锤冲击破碎的能量转化和能量效率特征，分析能量对破碎强度特性和破碎结果的影响关系。

1 落锤冲击破碎试验

1.1 试验装置与过程

试验在导杆式落锤冲击试验系统上完成，如图1所示。落锤质量为285 kg，在落锤上固定加速度感应器。系统通过激光测速仪测量冲击速度，同时记录冲击过程的加速度、作用力、位移与作用时间。试验时清洗导向杆并涂抹润滑油，减小摩擦力对落锤运动的影响。试验开始前对边长为100 mm的立方体试件进行预冲击试验，发现冲击高度为0.8 m时矿石发生有效的块体分离；落锤以0.8 m，0.9 m，1.0 m，1.1 m，1.2 m，1.3 m的高度冲击刚性底座上的BIF型磁铁矿石试件；冲击高度为1.3 m时矿石过度破碎，已满足试验对破碎程度的需要，且碎屑飞出较严重，为便于收集碎屑，保证粒度分析的准确性，不再使用更高的冲击高度。考虑试验数据的离散性，每个冲击高度下使用6个试件。试验结束后用0.074～75 mm孔径的标准筛筛分碎块，用高精度电子秤称量筛上的碎块质量，分析粒度分布特征。

图1 导杆式落锤冲击试验系统Fig.1 Drop weight impact test system with guide rod

1.2 试验材料选择与制备

BIF型磁铁矿在我国铁矿资源中占有主导地位，考虑试验材料的代表性，选取太古宙岩石发育的华北克拉通冀东-密云成矿带水厂铁矿的BIF型磁铁矿石。试验样品以条带状构造磁铁矿石为主，包含少量条纹状构造磁铁矿石。将试验样品切割打磨成100 mm×100 mm×100 mm标准试件，磁铁矿条带或条纹方向与水平面夹角为45°，保证冲击加载方向与矿石构造在空间关系上的一致性，矿石试件与放置方式如图2所示。

图2 磁铁矿石试件及其放置方式Fig.2 Magnetite specimen and placement method

1.3 能量转化关系与计算方法

落锤冲击动能转化为打击时的理论输入能、反弹能、振动能和声能；理论输入能的一部分被矿石吸收成为吸收能，一部分转化为矿石破碎过程中产生的热能、声发射能量、碎块动能以及传递至底座的能量。根据国军标GJB 150.18A和美军标MIL-STD-810G，系统计算磁铁矿石的冲击能、理论输入能、吸收能与能量效率的方法为

冲击能计算方法

EK=0.5mv2

(1)

理论输入能计算方法

EI=FmaxLmax

(2)

吸收能计算方法

(3)

能量效率计算方法

η=EA/EI

(4)

式中：m为落锤质量，kg；v为冲击速度，m/s；Fmax为最大作用力， kN；Lmax为试件破碎时最大变形，mm；a为冲击过程加速度，m/s2；t为作用时间，s。

1.4 试验结果

试验结束后，从系统中读取冲击速度、理论输入能、吸收能、能量效率、作用时间、峰值力和峰值位移等参数数值，计算每块矿石冲击破碎的应变率。收集矿石碎块，计算矿石碎块粒度分形维数[17]。在不同冲击高度下，磁铁矿石出现不同程度的破碎。在冲击高度小于1 m时，每组1～2个试件出现不完全破碎；冲击高度增加至1 m时，少量试件出现沙漏形或锥形大块；冲击高度大于1 m时试件全部破碎；随冲击破碎能量的增大，磁铁矿石破碎程度逐渐增大，冲击破碎能量与破碎强度参数和破碎结果呈较好的变化规律。

2 冲击破碎能量分析

2.1 冲击破碎能量的控制

试验中通过调节落锤高度改变冲击速度和冲击能。根据激光测速仪测量结果，在不同的冲击高度下，落锤的冲击速度分别为3.96 m/s，4.2 m/s，4.43 m/s，4.64 m/s，4.85 m/和5.05 m/s。根据能量数据的监测与计算结果，建立冲击能与平均吸收能和平均理论输入能的数值关系，如图3所示。冲击能与平均吸收能和理论输入能均有良好拟合关系，平均吸收能和理论输入能随冲击能的增大呈一次线性增长，通过调节冲击能可以控制矿石理论输入能和吸收能。

图3 冲击破碎能量关系Fig.3 Relations between different impact comminution energies

2.2 吸收能与理论输入能

图4为吸收能随理论输入能的变化关系。由图4可知，随着系统向矿石输入能量的增大，矿石吸收能基本呈线性增长的变化关系。系统输入的能量并不能全部被矿石吸收，当理论输入能大于1 400 J时，吸收能与理论输入能的关系变得较为离散，但仍保持线性增长的变化趋势。吸收能在输入能中的比例并不是固定不变的，即不同试件破碎的能量效率不是恒定的，这与不同试件内部结构差异有关。理论输入能是最大冲击力与最大变形的乘积，不同试件所能承受的最大冲击力与最大变形的能力是不一样的，因此不同试件的理论输入能不相同；在较高的理论输入能条件下，不同试件承受的冲击力与变形的差异较大，基于冲击力与变形积分得到的吸收能值出现较大的离散现象，但吸收能与理论输入能整体表现出显著的线性关系。

图4 吸收能与理论输入能Fig.4 Absorbed energy and theoretical input energy

2.3 能量效率分析

2.3.1 能量效率的变化特征

图5是每种冲击高度下平均能量效率与冲击能的关系，图6是试件破碎的能量效率与理论输入能的关系。由图5可知，随着冲击能的增大，不同高度下的平均能量效率呈一次函数线性降低关系，较低的冲击能量有利于能量效率的提高。由图6可知，落锤冲击破碎时磁铁矿石吸收能占理论输入能的比例主要为25%～45%，平均为35.3%，少量试件的能量效率大于45%。随着矿石理论输入能的增大，理论输入能在0～850 J内，能量效率以较大的速率降低；在超出850 J的区间内，能量效率以较小的速率继续降低。理论输入能较低时，试件受到的最大作用力和最大变形值较小，试件承受的冲击力与变形的积分在最大作用力和最大变形乘积中比例较大，即能量吸收效率较高。随着理论输入能的增大，试件内部损伤活动加剧，冲击过程中试件内部发生较大的能量耗散，用于试件变形的能量比例降低，导致能量效率降低。在较低的理论输入能范围内，理论输入能的增大使试件损伤破坏程度的变化更为显著，吸收能在理论输入能的比例降低速率较大。

图5 平均能量效率与冲击能Fig.5 Average energy effect and impact energy

图6 能量效率与理论输入能Fig.6 Energy effect and theoretical input energy

2.3.2 应变率对能量效率的影响

图7为能量效率与应变率的关系曲线。由图7可知，质量为285 kg的落锤在高度为0.8～1.3 m内冲击BIF型磁铁矿石的应变率范围集中在35～110 s-1，个别试件的应变率超出150 s-1。随着应变率的增大，能量效率整体呈指数降低的变化趋势。但是在应变率小于65 s-1的范围内，能量效率较高，但降低速率较快；在应变率大于65 s-1的范围内能量效率降低速率变缓。较低应变率条件下，裂隙萌生和扩展缓慢，能量耗散少，吸收在试件中的能量相对较多，故能量效率较高；在较高应变率下试件变形速率大，试件内部裂隙扩展速率快，能量来不及大量积聚就被消耗，故能量效率较低，试件变形速率对能量转化效率起主导作用。

图7 能量效率与应变率的关系Fig.7 Relation between energy effect and strain rate

2.3.3 作用时间对能量效率的影响

图8反映了落锤冲击磁铁矿石的作用时间与能量效率的关系。随着冲击作用时间的延长，能量效率基本上呈一次函数线性增大的变化。落锤冲击磁铁矿石时，在矿石内产生正弦应力波，并在试样内来回传播，使矿物颗粒发生位移，试件变形。冲击作用时间越长，应力波在试件内传播的时间越长，试件内积聚的变形能的概率越大，吸收能比例越大，能量效率就会越高，延长冲击破碎作用时间可以提高能量利用效率。

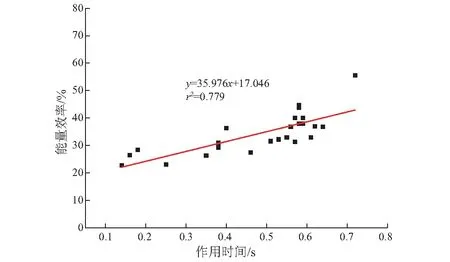
图8 能量效率与作用时间的关系Fig.8 Relation between energy effect and impact time

3 能量密度对动态强度特性的影响

3.1 冲击能密度与动态强度参数

冲击能密度为系统施加给单位体积矿石的冲击能，图9和图10分别为冲击能密度与平均动态强度和平均最大应变的关系图。随着冲击能密度的增大，平均动态强度和平均最大应变均呈一次函数线性增长的变化，且相关性很好，说明增大冲击能可以提高磁铁矿石平均动态强度和平均最大应变。

图9 平均动态强度与冲击能密度的关系Fig.9 Relation between average dynamic strength and impact energy density

图10 平均最大应变与冲击能密度的关系Fig.10 Relation between average maximum strain and impact energy density

3.2 吸收能密度与动态强度参数

吸收能密度是单位体积矿石吸收的能量，图11和图12分别为单位体积吸收能与动态强度和最大应变的关系图。由图11可知，落锤冲击条件下，BIF型磁铁矿石的动态强度与吸收能密度正相关，吸收能密度越大，矿石动态强度越高。在试验范围内，矿石试件吸收能量越多，矿物颗粒运动的动力越强，冲击过程中矿物颗粒首先向孔隙裂隙方向运动，增加矿石密实度，使得矿石动态强度增大。由图12可知，矿石试件的最大应变集中在0.025～0.03内，不随吸收能密度的变化单调增大或减小，这是由于矿石内原生孔隙、裂隙在空间上的分布是随机的，在不同的能量作用下，矿石发生随机变形，但BIF性磁铁矿石承受变形的能力是有一定范围的。

图11 动态强度与吸收能密度Fig.11 Dynamic strength and absorbed energy density

图12 最大应变与吸收能密度Fig.12 Maximum strain and absorbed energy density

4 能量对破碎结果的影响

4.1 破碎能量分形理论

脆性岩石破碎产品的粒度均具有分形特性，分形维数越大表示岩石破碎越严重。根据分形概念和格里菲斯能量平衡理论，破碎能量与破碎产品粒度的分形维数之间具有指数相关性，如式(5)所示[18]。

E∝rφ,φ=0.5(Ds-3)

(5)

式中：E为单位体积能量密度；r为破碎产品粒度；Ds为粒度分布的分形维数。

岩石破碎粒度分布的分形维数与单位质量输入能之间存在函数相关性，如式(6)所示[19]。

(6)

式中：E为单位质量冲击能；K1，K3为拟合常数；K2为材料常数。

由式(5)和式(6)可知，能量与矿岩石破碎粒度分布的分形维数呈正相关的函数关系，BIF型磁铁矿石属于脆性岩石材料，假设磁铁矿石冲击破碎后的产品粒度具有分形特性，且分形维数与破碎能量之间保持一定的函数关系。为分析磁铁矿石冲击破碎的粒度特性，研究能量对BIF磁铁矿石冲击破碎粒度分布特性的影响关系，基于分形理论提出适合计算磁铁矿石冲击破碎分形维数的方法，建立能量与分形维数的函数模型，验证假设的正确性。

4.2 产品粒度分形维数计算方法

磁铁矿石破碎是能量消耗的过程，根据破碎分形的基本定义[20]，破碎颗粒粒径和颗粒数量之间的分形关系为

N(R>r)∝r-Ds

(7)

式中：r为破碎产品的粒径；N(R>r)为粒径大于r的颗粒数量；D为颗粒数量—粒度分布的分形维数。

根据颗粒数量与特征粒径之间的分形关系，将破碎产品颗粒总数量Nm与最大粒径rm代入式(7)，可得

N(R>r)/Nm=(r/rm)-Ds

(8)

根据破碎产品颗粒数量与粒径分布数据，将式(8)等式两边对数变换，可得到分形维数。

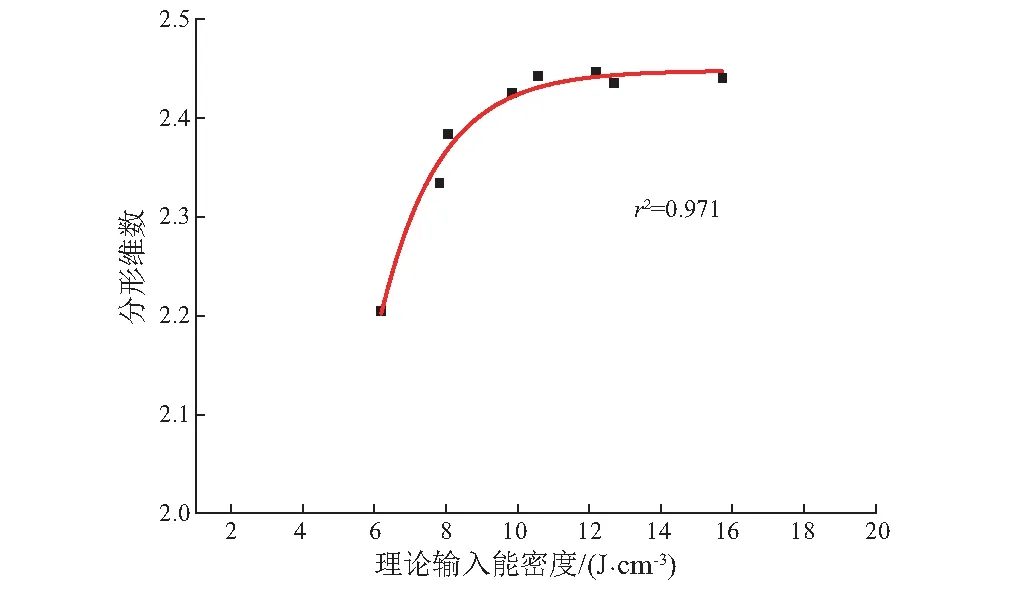
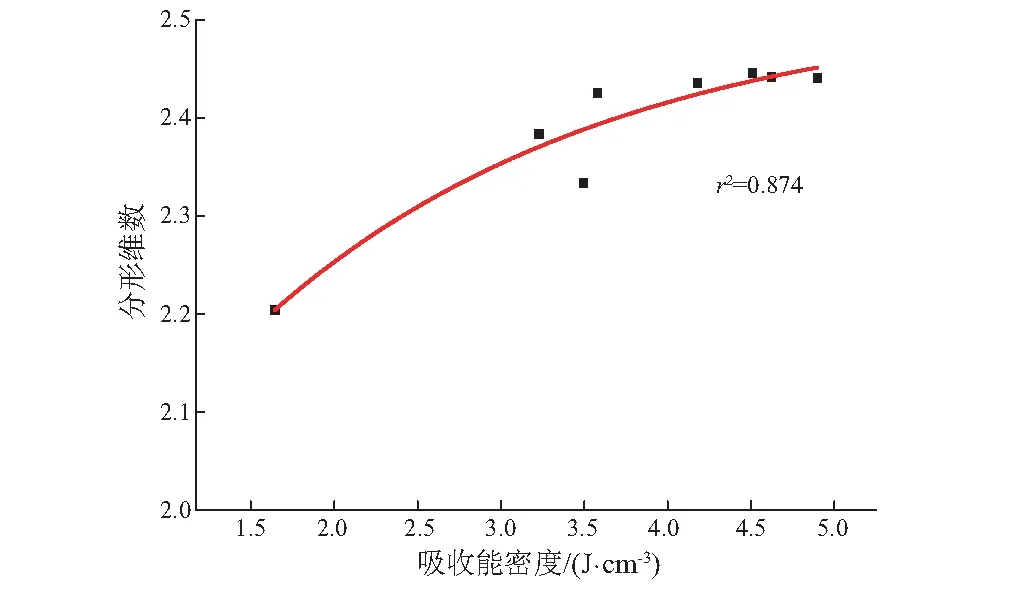
磁铁矿石冲击破碎时，随着产品粒径的减小，颗粒数量急剧增加，应用颗粒数量—粒径分布数据计算分形维数的方法很不方便。使用标准筛筛分测试产品质量分布是描述岩石破碎特性的常用方法，Zhang等[21]认为可以采用不同粒径颗粒数量积分的方法得到某种网目筛下累计质量。

假设破碎产品颗粒最小粒径为dmin，r∈[dmin,d]，粒径大于r的颗粒数量为N(R>r)，且R

(9)

式中：M(r

N(R>r)=Cr-Ds

(10)

式中：C为颗粒数量与分形关系的拟合常数。对式(10)进行微分

dN(R>r)=-CDsr-Ds-1dr

(11)

将式(11)代入式(9)，并对粒径积分可得粒径小于d的颗粒累积质量计算式

(12)

当d=dmax时，破碎产品总质量计算式为

(13)

冲击破碎时最小颗粒粒径远小于0.074 mm，假设最小粒径等于0，将式(12)和式(13)进行比例换算，得到矿石冲击破碎产品的累积质量—粒度分布方程

Y=M(r

(14)

对式(15)进行对数变换得到包含Ds的矿石冲击破碎产品质量累积概率分布函数

F(d)=ln(M(r(3-Ds)ln(d/dmax)

(15)

由式(15)可知冲击破碎产品的累积质量——粒度分布的双对数曲线斜率n=3-Ds，从而求得分形维数Ds。可见，用标准筛筛分的方法得到冲击破碎产品的累积质量——粒度分布数据，对数变换处理后通过数值拟合即可得到不同能量下的粒度分形维数，该方法简单易行。式(15)是由式(7)和式(8)通过微积分的方法推导演化而来，与刘瑜等人基于煤块颗粒质量提出的分形维数计算公式基本一致[22]。通过累积质量——粒度分布数据计算分形维数符合破碎分形的基本概念，可用于描述磁铁矿石冲击破碎结果。

4.3 能量密度与分形维数

收集BIF型磁铁矿石碎块，采用标准筛筛分和高精度称重的方法测试破碎产品的粒级组成，计算各网目筛下累积质量百分数，得到破碎产品累积质量概率分布。以冲击能、输入能和吸收能与试件体积的比值作为能量密度，通过式(16)拟合计算破碎产品的分形维数，如表1所示。由表1中分形维数的计算结果，BIF型磁铁矿石冲击破碎产品的分形维数集中在2.20～2.45，破碎结果具有良好的分形特性，基于累积质量概率分布计算的分形维数可以很好的描述BIF型磁铁矿石冲击破碎的粒度特性。为了明确破碎能量与破碎结果的映射关系，分别绘制冲击能密度、输入能密度和吸收能密度与分形维数的关系曲线，如图13～图15所示，构建能量密度与破碎结果的函数关系模型，如表2所示。

表1 破碎能量密度与破碎产品粒级分布

由图13～图15和表2可知，BIF型磁铁矿石冲击破碎产品的分形维数与能量密度之间具有良好的函数关系，研究范围内分形维数与能量密度呈负指数增长的变化规律，增大冲击破碎的能量密度可以提高产品粒度的分形维数，增加破碎程度，但是分形维数的增长速率随能量密度的增大而减小。这种能量与分形维数的相关关系与Brown摆锤冲击岩石试验结果一致。BIF型磁铁矿石冲击破碎是裂隙快速扩展导致块体分离的过程，不同规模的裂隙切割出不同尺寸的碎块。根据文献[23]，裂隙的扩展是在能量驱动下发生的自相似行为，因此破碎产品必然存在分形特性，产品粒度分布与能量之间存在定量关系，冲击破碎能量越大，分形维数越大，但能量增大到一定程度时分形维数趋于定值。与冲击能密度和理论输入能密度相比，分形维数与吸收能密度的拟合度偏小，这是由于矿石吸收能量的能力不仅取决于冲击能和理论输入能的大小，而且受内部结构构造的影响。BIF型磁铁矿石构造包括条纹状和条带状，条纹状构造矿石的磁铁矿条纹宽为1～3 mm，条带状构造矿石的磁铁矿条带宽大于3 mm，条纹与条带宽度以及矿物颗粒嵌布特征的不同，导致试件能量转化效率和破碎结果出现一定差异。