类车体尾迹流动非定常特性

2019-04-01王冰心杨志刚

同济大学学报（自然科学版） 2019年1期

王冰心，杨志刚,2，朱晖

(1. 同济大学上海地面交通工具风洞中心，上海 201804；2. 北京民用飞机技术研究中心，北京 102211)

作为汽车气动减阻方法之一的流动主动控制法包括定常控制技术与非定常控制技术，其中后者较前者更具优势.Brunn等[1]在35°后倾角Ahmed类车体背部斜面上侧分离线处采用非定常控制技术，实现减阻率2.5%；Krentel等[2]在25°后倾角Ahmed类车体背部斜面下侧分离线处采用非定常控制技术，实现减阻率5.7%；Pastoor等[3]采用非定常控制技术实现了上下剪切层同步，减阻率达15%.非定常主动控制技术运用的成功与否依赖于对车体绕流场的流动结构及其非定常运动特性的研究[4].

针对Ahmed类车体，以往的数值与实验分析指出其尾迹区由3个主要部分组成：背部斜面上的分离泡、背部斜面侧“C柱”处卷起的拖曳涡对及尾部垂直面后部的回流区[5]，气动阻力与这三种相干结构的相互作用有直接的关系[6].Minguez等[7]用高阶大涡模拟法研究发现在ReH=7.78×105时背部斜面出现主频，对应的Str=0.27，垂直面后部回流区出现主频，对应的Stb=0.42，并指出背部斜面马蹄涡的频率起主导作用.

Thacker等[8-9]研究了不同雷诺数下背部斜面的主频，Str=0.18～0.21分别对应雷诺数ReH=(3.89～7.78)×105，相比其他研究其结果偏小，且指出马蹄涡对应的频率不是背部斜面的主导频率，而应为高频特性，与文献[7]相矛盾.Heft等[10]在ReH=7.78×105时得出背部斜面主频Str=0.18；Pierric等[4]研究了不同雷诺数时背部斜面处与垂直面处流动的主频特性，Str=0.29～0.43与Stb=0.44～0.45对应ReH=(3.89～7.78)×105，指出主频会随雷诺数增大而增大，而高频特性对应由KH不稳定性造成的剪切层卷起频率.Zhang等[11]由主频特性与雷诺数关系的拟合曲线得出在ReH=7.78×105时，Str与Stb分别为0.52与0.46.由此可知，针对Ahmed类车体尾迹区非定常特性的研究结果存在明显差异.Jean-Francois等[12]定性地解释了背部斜面分离泡与“C柱”拖曳涡对存在竞争作用关系：较强较大的背部斜面分离泡会产生较低的背压，在使阻力增加的同时，导致从背部斜面侧“C柱”处卷起的拖曳涡对更强；另一方面，较强的“C柱”拖曳涡对在其涡核中心诱导出较大的低压区，从而延缓了背部斜面分离泡的分离，而且较强的“C柱”拖曳涡对诱导流体产生的下洗作用较强，减小了背部斜面分离泡尺度从而使阻力减小；但作者并未对此作进一步定量的论证.因此，有必要对Ahmed类车体尾迹区不同相干结构的相互作用进行深入研究.

本文以大涡模拟为手段，在高雷诺数(ReH=7.78×105)下，获取25°后倾角Ahmed类车体尾迹区不同部位处流场参数的时变信息，依据所得数据频谱分析结果，进一步明确尾迹区流动的非定常特性.

1 数值仿真模型与计算方法

1.1 数值仿真模型

采用全尺寸 Ahmed类车体作为研究对象，具体结构及尺寸如图1所示.整车置于长×宽×高为8.352 m×2.723 m×1.152 m的计算域中，车头距入口1.566 m，车尾距出口5.742 m，阻塞比3.57%.

为降低数值黏性，在计算域内采用空间切块映射法构造六面体网格，如图2所示.车身表面网格尺寸<4 mm，车身表面第一层边界层网格高度为0.03 mm，地面第一层网格高度为0.05 mm，以1.10的增长率生成20层形成边界层网格；边界层网格以1.15的比例与外侧体网格过渡；在确保第一层网格高度量纲为一参数Y+≤3的前提下，体网格总数为2 200万单元，图3显示了中截面体网格结构.

图1 类车体构造及尺寸(单位：mm)Fig.1 Structure and size of Ahmed body(Unit：mm)

图2 计算域分块结构Fig.2 Blocks structure of computational domain

图3 体网格结构Fig.3 Structure of volumetric mesh

1.2 数值模拟方法

流场求解基于Fluent仿真平台完成，湍流模型采用LES框架中的动态 Smagorinsky-Lilly亚格子模型.与传统Smagorinsky亚格子模型相区别，Smagorinsky-Lilly亚格子模型计算涡黏系数μt的方程为

(1)

(2)

(3)

Ls=min(kd,CsV1/3)

(4)

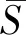
本文Ma<0.3，所以不考虑空气压缩性，认为空气的温度、参考压强、黏性及密度不变，表1列出了计算条件下的主要物性参数.边界条件见表2，来流(V0)方向垂直于计算域进口.

表1 物性参数Tab.1 Physical parameters

表2 边界条件Tab.2 Boundary conditions

采用SIMPLEC(意为“协调一致的求解压力耦合方程组的半隐式方法”)压力速度耦合算法进行迭代计算，松弛因子为默认值.基于可实现K-ε湍流模型得到流场的定常解进行LES模型的非定常计算，非定常时间步长为1×10-4s，单位时间步进行30次子迭代.整个计算共历经30 000个时间步长，将最后5 000个时间步长计算结果用于数据分析.

1.3 数值方法初步验证

为验证数值方法的有效性，以来流速度为比例尺，在对称截面作流向速度型曲线，并与实验数据进行对比[15]，如图4所示，X为流向尺度，Z为垂向尺度.由图可知：计算结果与实验值符合良好，且在尾迹区的对比一致性高于斜面区.Re=7.78×105时气动阻力系数CD的计算结果为0.317 9，实验值为0.312 0[4]，误差1.9%.

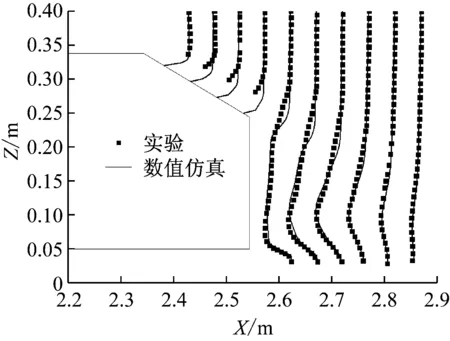
图4 流向速度型曲线Fig.4 Profile of longitudinal velocity

2 数值结果与分析

Ahmed类车体尾迹区展向流动结构如图5所示.主要涡结构由尾迹区上、下展向涡对(涡核中心N1、N2)及斜面分离泡(涡核中心N3)构成.尾迹区上、下展向涡对中、上侧展向涡的尺度较大，下侧展向涡的尺度较小.上、下展向涡对形成鞍点S1.

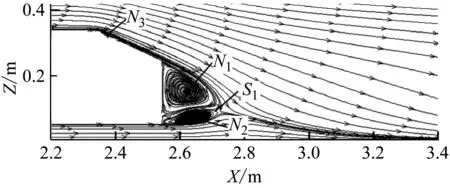
图5 对称截面Y=0时均流线Fig.5 Time-averaged streamlines of the symmetric plane

使用Q准则显示类车体尾迹区空间涡系结构，如图6 所示.从图6可知，Ahmed类车体尾迹分离结构主要可划分为3个部分，即背部斜面上的分离泡、从背部斜面侧边卷起的拖曳涡以及垂直面处回流区.

控制箱的操纵面板和内部显示器是主要的人机交互界面。扩展设备中包括键盘、鼠标、外置显示器等外部交互设备。水下本体的网络摄像机为大华的球型网络摄像机。

图6 Q准则等值面(Q=3.13×105 s-2)Fig.6 ISO-surface of vortices in the wake using Q- criterion when Q=3.13×105 s-2

2.1 背部斜面分离泡非定常特性

在背部斜面上方布置A1～A4测点如图7所示，X方向坐标原点设置在计算域入口，Y方向坐标原点设置在中间对称面，Z方向坐标原点设置在地面.点A1～A4的坐标分别为[2.373,0,0.339]、[2.430,0,0.326]、[2.487,0,0.315]、[2.544,0,0.302]，单位m.

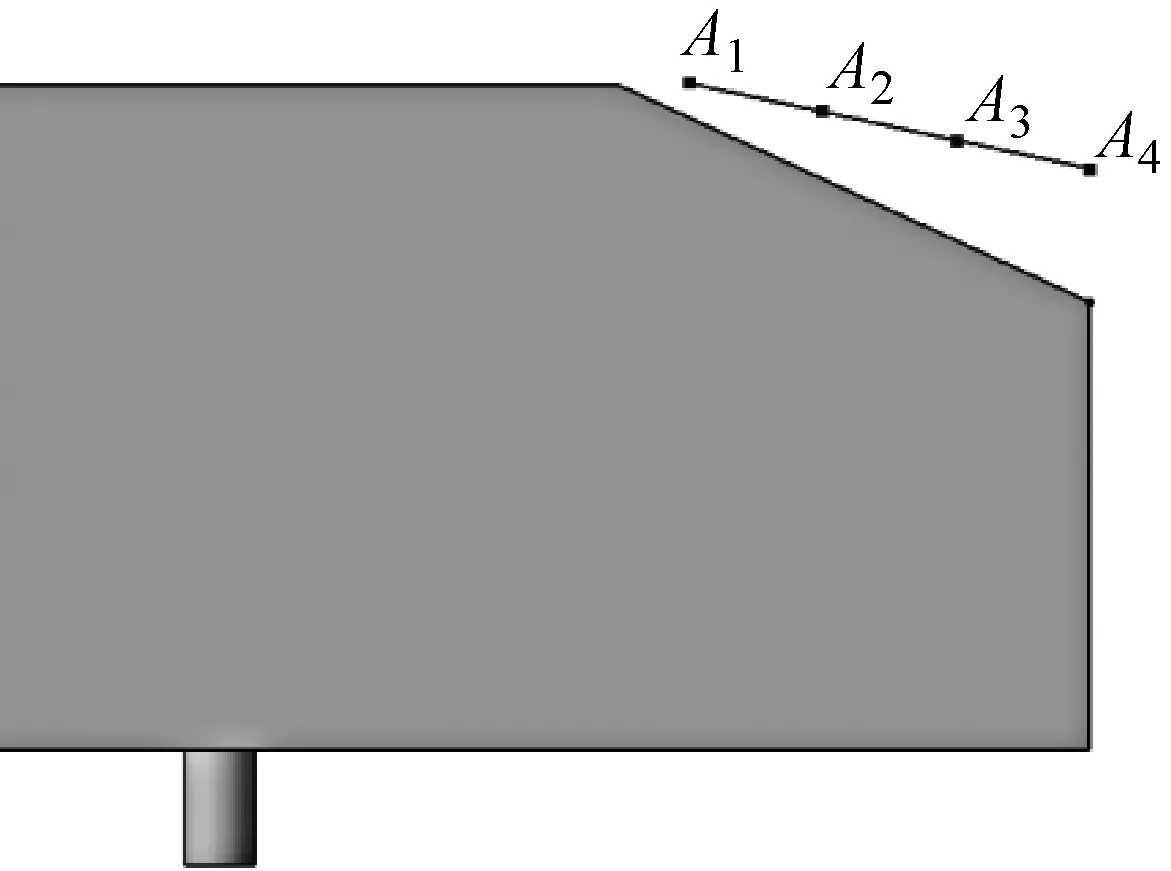
图7 A1～A4测点分布Fig.7 Layout of sampling points from A1～A4

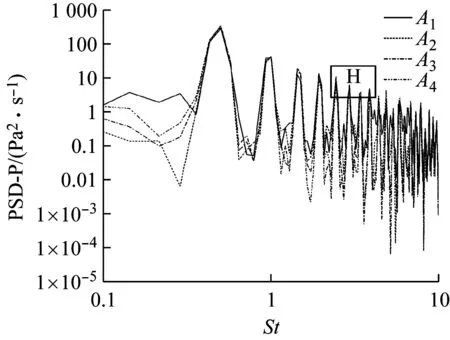
图8 A1～A4测点压力功率谱Fig.8 PSD of the pressure at sampling points from A1 to A4

背部斜面分离泡拍击振动过程表现为分离泡持续放大(剪切层不断卷起并累积)与缩小(大尺度相干结构脱落流向下游)的交替过程.而大尺度相干结构起源于剪切层的卷起，而剪切层卷起的直接原因为KH不稳定性.根据不稳定性理论，如果瞬时扰动取消后，扰动随时间增长且向下游传播从而离开扰动的初始空间位置，在空间固定位置处，扰动将逐渐衰减，最终保持平静，那么流动是对流不稳定的；如果瞬时扰动取消后，扰动在初始空间位置处随时间增长，同时向上、下游传播，最终导致整个空间的扰动随时间增长，那么流动是绝对不稳定的.

如图9所示，在背部斜面壁面上布置T1～T4测点，坐标分别为[2.344,0,0.337]、[2.349,0,0.335]、[2.392,0,0.315]、[2.406,0,0.309]，单位m.T1点、T2点在分离线附近，T3点、T4点在附着线附近.测点压力互谱与相谱分析结果如图10～图12所示，其中互相关函数见式(5).Pxy(f)为信号X与信号Y的互功率谱密度；Pxx(f)、Pyy(f)分别为信号X与信号Y的自功率谱密度.表3给出目前较为公认的相关程度划分标准.

(5)

由图10a可知，T1、T2测点互谱曲线在分离泡拍击振动特征频率Str=0.49附近的低频带内呈现中度相关性，表明低频运动强烈地影响了分离线附近区域的流动相关性.而在该低频带对应的相谱曲线图10 b中，在0°相位角下相谱曲线几乎不随频率变化，表征了与分离泡拍击振动对应的低频运动是一种绝对不稳定性运动.如图11所示，在分离泡拍击振动特征频率Str=0.49附近的低频带内,T1,T3测点互谱曲线呈现中度相关性，表明低频运动影响了整个背部斜面分离泡，进一步证实了与分离泡拍击振动对应的低频运动是一种绝对不稳定性运动.图12 a显示T3、T4测点的互谱曲线在表征KH不稳定性的高频带内呈现中度相关性，图12 b所示相谱曲线在从低频至高频的范围内呈现准线性关系，这证实了具有高频特性的KH不稳定性是一种对流不稳定性[9].文献[9]得出对流速度Vc=0.5V0的结论，并给出了从相谱曲线推导Vc的表达式如下：

图9 T1～T4测点分布Fig.9 Layout of sampling points from T1 to T4

a 互谱

b 相谱图10 T1与T2测点压力互谱与相谱

Fig.10Coherenceandphasefunctionsfromcross-spectraofthepressurebetweensamplingpointsT1andT2

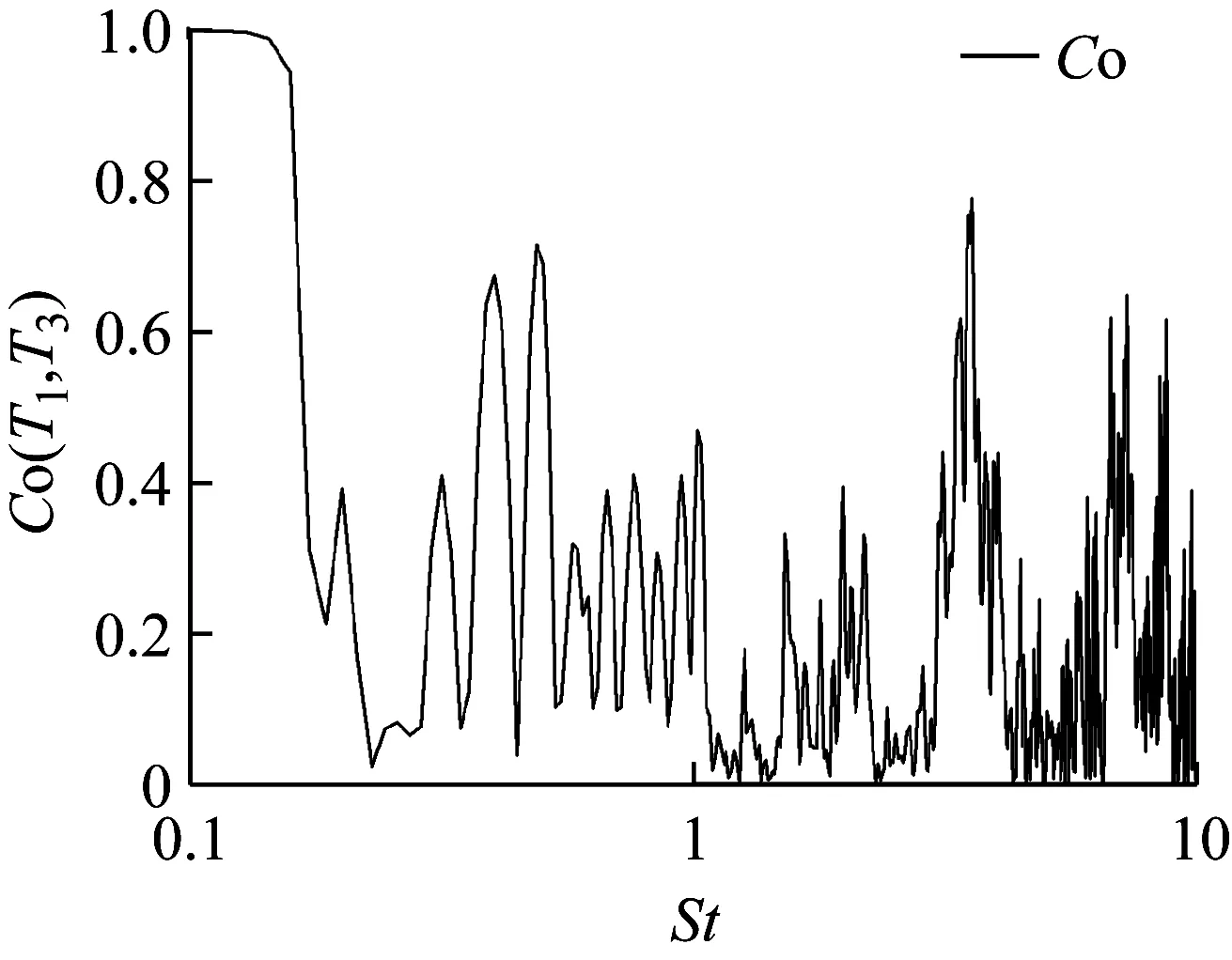
图11 T1与T3测点压力互谱Fig.11 Coherence function from cross-spectra of the pressure between sampling points T1 and T3

a 互谱

b 相谱图12 T3与T4测点压力互谱与相谱

Fig.12Coherenceandphasefunctionsfromcross-spectraofthepressurebetweensamplingpointsT3andT4

表3 相关程度Tab.3 Relationship correlation

(6)

式中：ΔL为两测点间距离；H为车高；dθ/dSt为相谱曲线中相位角θ对于频率St的斜率.由图12 b中的T3、T4相谱曲线得到Vc≈0.56V0，与文献[9]的结论基本符合，进一步验证了数值计算的有效性.

2.2 “C柱”拖曳涡对非定常特性

如图13所示，在背部斜面两侧上方布置了关于Y=0平面对称的B1～B4、C1～C4两列测点，其坐标为[2.373,∓0.194 5,0.339]、[2.430,∓0.194 5,0.326]、[2.487,∓0.194 5,0.315]、[2.544,∓0.194 5,0.302]，单位m.图14为B、C两列测点压力功率谱的分析结果，可知：“C柱”拖曳涡对(s)的特征频率为Sts=0.49，随着流动往下游发展，峰值频率对应的能量增强.

图13 B1～B4与C1～C4测点分布Fig.13 Layout of sampling points from B1 to B4 and from C1 to C4

图15为A、C两列对应测点压力互谱与相谱分析结果.由图可知，A、C测点压力脉动在特征频率St=0.49时具有高度或中度相关性，且以同相位振动，表明背部斜面处的分离泡与“C柱”拖曳涡对具有很强的耦合作用：流过背部分离线的流体远离壁面，从而在背部斜面处产生低压区；流过斜面侧边的流体在外部流场高压与斜面低压的压差作用下产生向内旋转的“C柱”拖曳涡对，在拖曳涡对的诱导作用下流体向斜面下洗.

图16～图19为B、C两列对应测点压力与速度分量互谱与相谱分析结果.可知：“C柱”拖曳涡对的压力脉动在特征频率Sts=0.49时具有显著的高度相关性，且以同相位振动；X、Y方向上的运动相对纵向对称面呈高度对称性，且在Y方向的运动特征为同时向对称面靠近或远离的摆动；Z方向速度呈低度相关或不相关特性，相谱在特征频率Sts=0.49时存在既非0°又非180°的相位差，表明Z方向上的流动随机性强.

a B1～B4测点

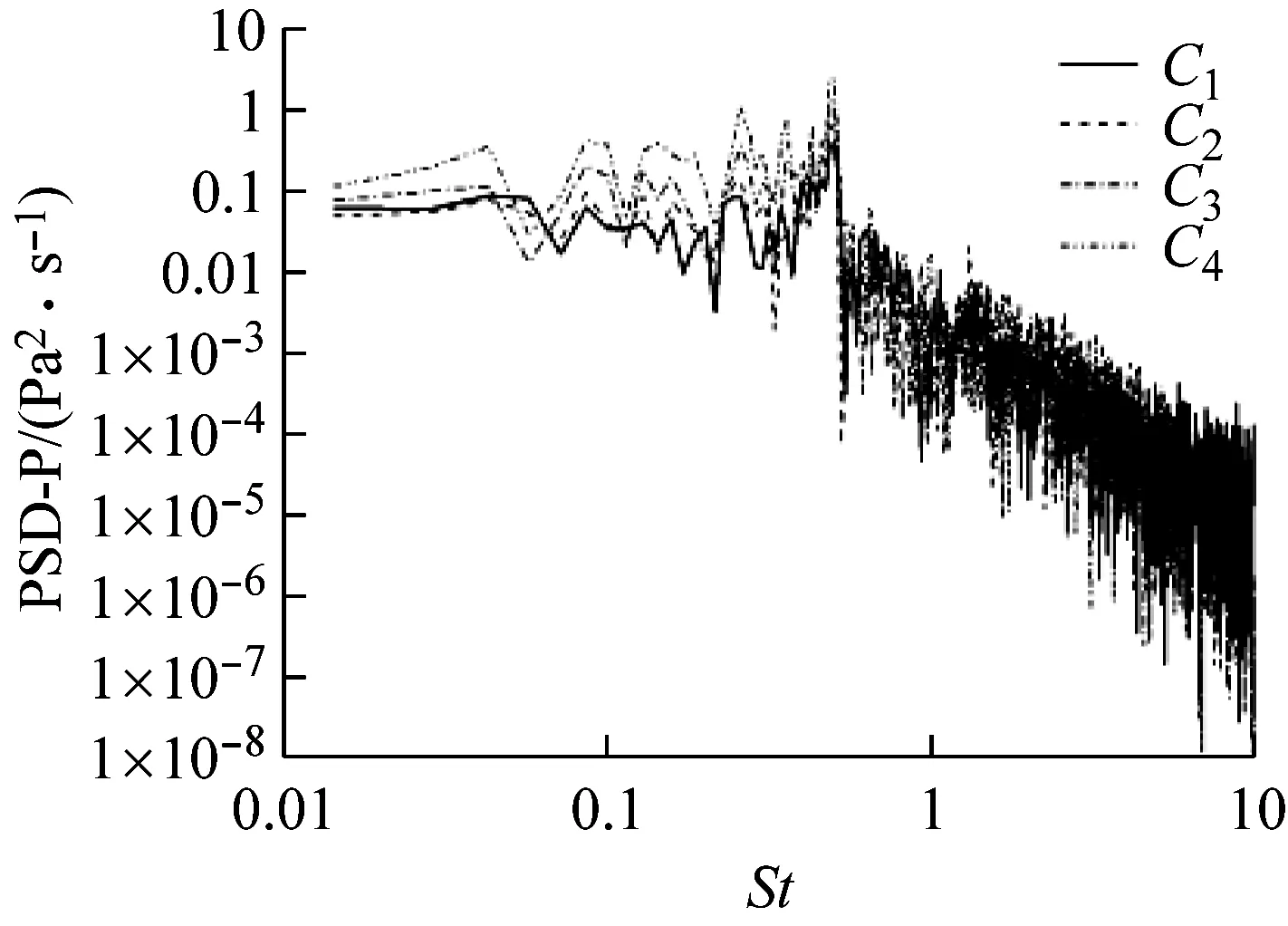
b C1～C4测点图14 B1～B4与C1～C4测点压力功率谱Fig.14 PSD of the pressure at sampling points from B1 to B4 and from C1 to C4

a 互谱

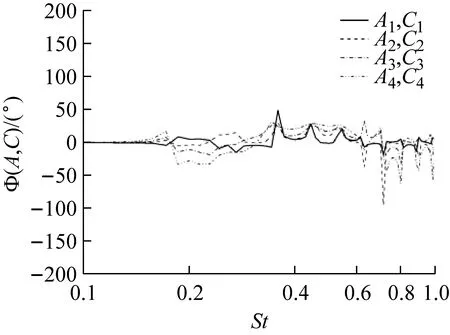
b 相谱图15 A列与C列测点压力互谱与相谱

Fig.15Coherenceandphasefunctionsfromcross-spectraofthepressurebetweensamplingpointsA-seriesandC-series

a 互谱

b 相谱图16 B列与C列测点压力互谱与相谱

Fig.16Coherenceandphasefunctionsfromcross-spectraofthepressurebetweensamplingpointsB-seriesandC-series

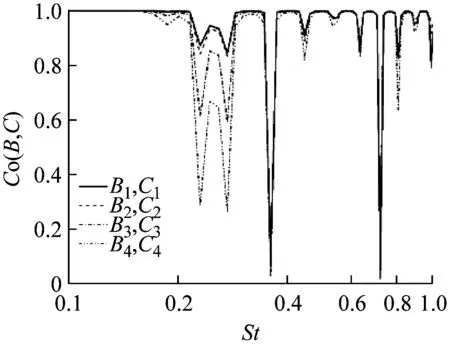
a 互谱

b 相谱图17 B列与C列测点X向速度互谱与相谱

Fig.17Coherenceandphasefunctionsfromcross-spectraoftheX-velocitybetweensamplingpointsB-seriesandC-series

a 互谱

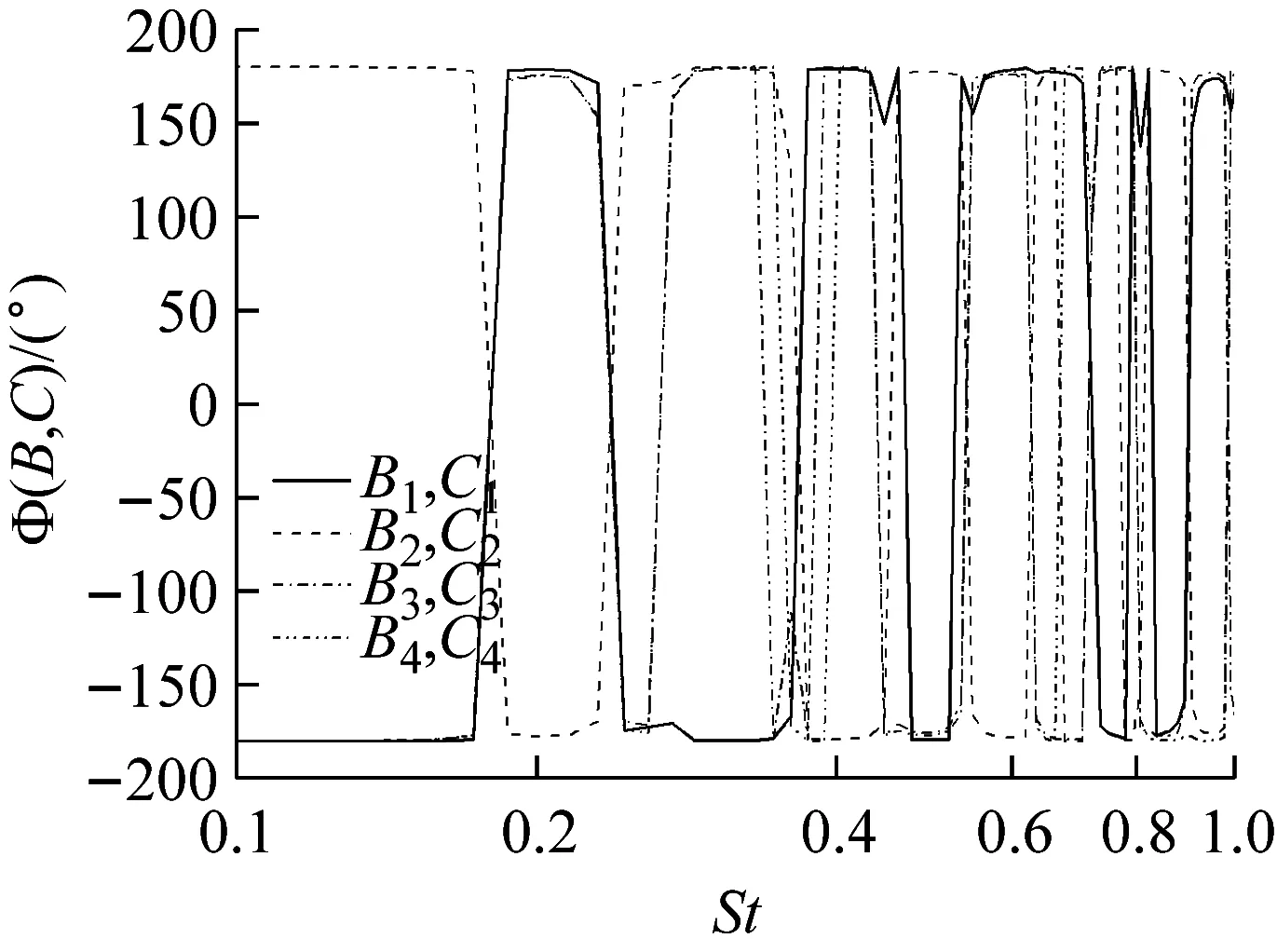
b 相谱图18 B列与C列测点Y向速度互谱与相谱

Fig.18Coherenceandphasefunctionsfromcross-spectraoftheY-velocitybetweensamplingpointsB-seriesandC-series

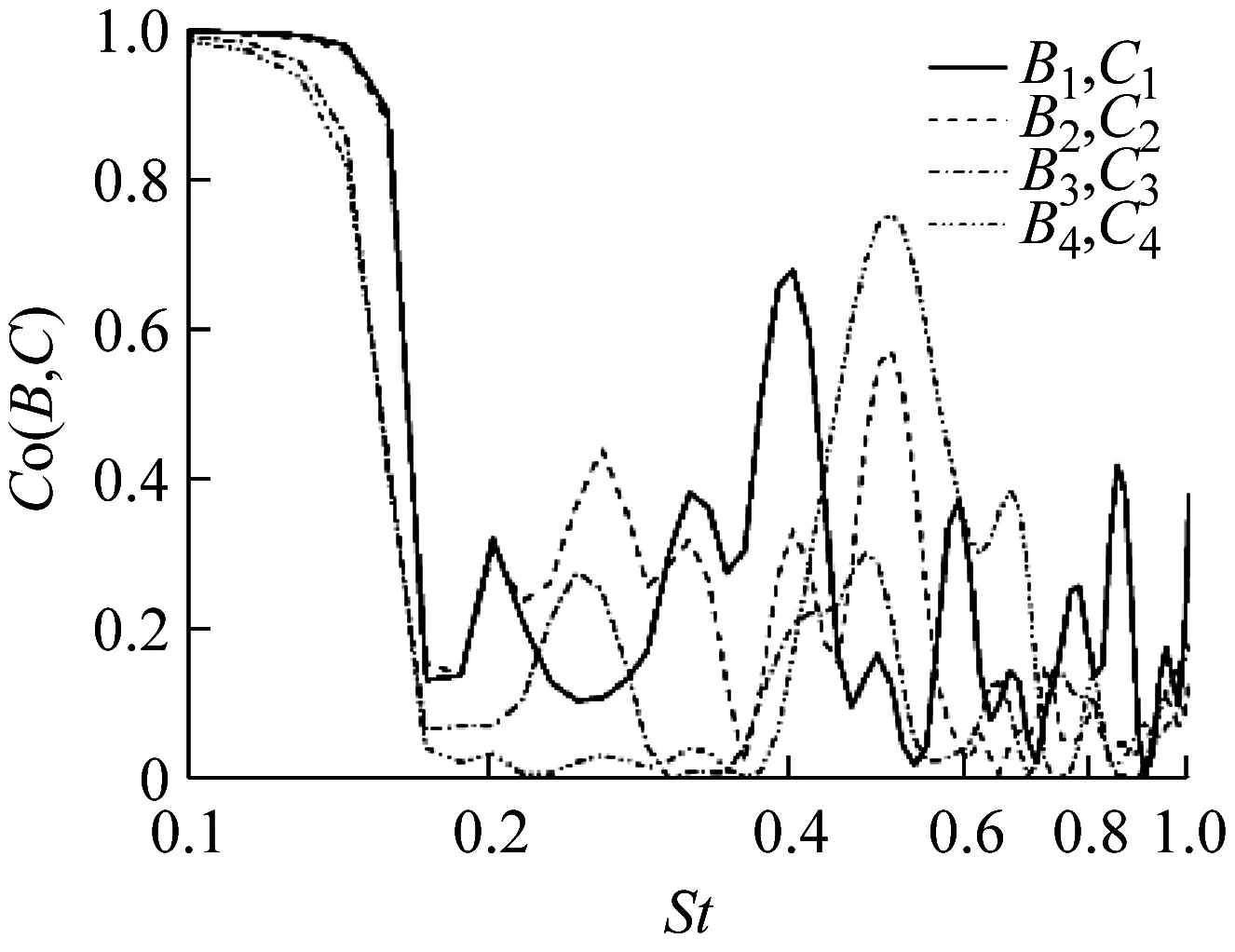
a 互谱

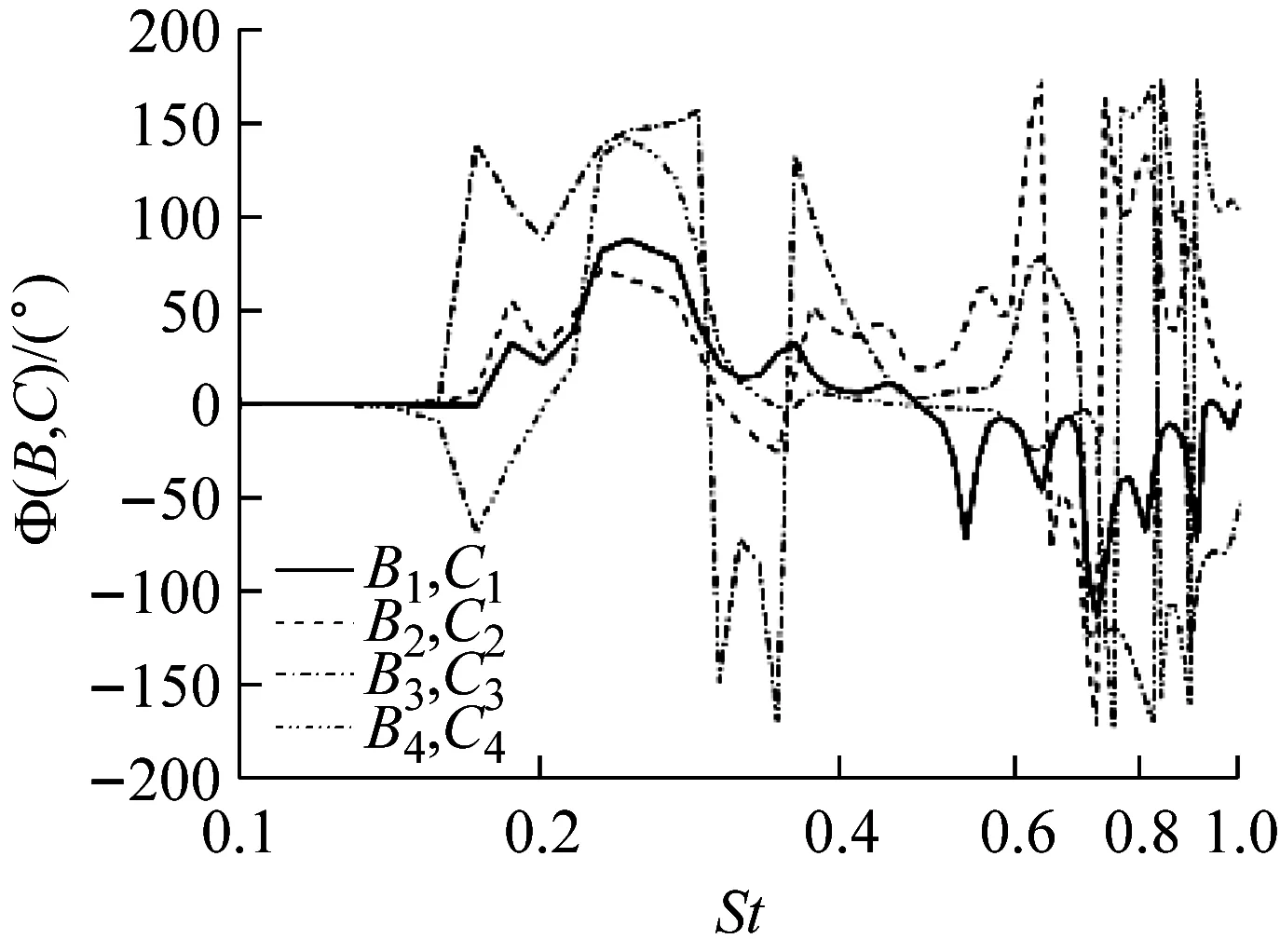
b 相谱图19 B列与C列测点Z向速度互谱与相谱

Fig.19Coherenceandphasefunctionsfromcross-spectraoftheZ-velocitybetweensamplingpointsB-seriesandC-series

2.3 回流区流动非定常特性

垂直面后部回流区内布置的由D到O共12列测点如图20所示，每列均布6个测点，由下至上编号为1～6.其中编号为1的测点Z坐标为0.050 m，编号为6的测点Z坐标为0.231 m；D～G、L～O列测点Y坐标为m，H～K列测点Y坐标为0 m；D、H、L列测点X坐标为2.611 m，E、I、M列测点X坐标为2.700 m，F、J、N列测点X坐标为2.813 m，G、K、O列测点X坐标为3.014 m.D6～G6与L6～O6测点压力脉动功率谱表征了“C柱”拖曳涡对发展至回流区的频谱特性，结果见图21.在回流区中“C柱”拖曳涡对的特征频率Sts=0.49，与图14对比可知：由于与回流区中的流体相掺混，加强了质能交换，使得回流区中拖曳涡对的能量有显著提高；但随着向下游发展，高频能量衰减更快.

图22为D6～G6与H6～K6对应测点压力互谱与相谱的分析结果.由图可知，压力脉动在特征频率Stb=0.49时呈中度相关，但相谱上存在既非0°又非180°的相位差.对比图15可知，拖曳涡与回流区中展向涡的相关度明显减弱，可见拖曳涡对与尾迹区展向涡之间虽相互干涉，但不存在耦合现象.

图23～图26显示了D6～G6与L6～O6对应测点压力与速度分量互谱与相谱的分析结果.在回流区近壁面处(D6、L6)，两侧拖曳涡的压力脉动呈中度相关，随着向下游发展，由于能量耗散作用，其相关程度逐渐减弱；在M、E位置受到回流区鞍点的影响，其相关程度最弱.相谱上在特征频率Stb=0.49时存在既非0°又非180°的相位差，由此可知两侧拖曳涡的压力脉动并不对称.拖曳涡对在回流区中的速度信号呈低度相关或不相关特性，都以既非同相位又非反相位振动，表明两侧拖曳涡在回流区中的非定常特性较为独立，无对称性特征.

H～K列测点压力功率谱分析结果如图27所示.回流区上下剪切层卷起的展向涡特征频率Stb=0.49，上、下剪切层卷起的展向涡向下游发展，其能量在流向位置I处达到最大，继续向下游发展能量逐渐耗散.根据上、下侧测点功率谱密度的曲线斜率可推断：上侧展向涡的耗散较快，下侧展向涡由于地面效应的存在，其在流场中的持续时间更长.

图20 D～O列测点分布Fig.20 Layout of sampling points from D-series to O-series

图21 回流区内拖曳涡对测点压力功率谱

Fig.21PSDofthepressureatsamplingpointswithintheC-pillarvorticessheddingintotherecirculationtorusbehindtheverticalbase

a 互谱

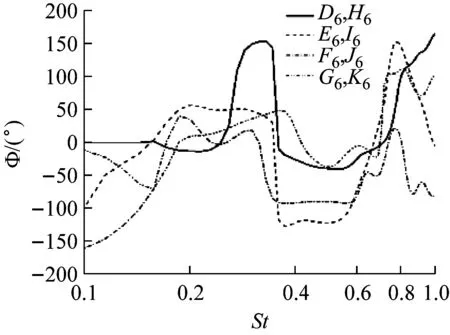
b 相谱图22 D6～G6与H6～K6对应测点压力互谱与相谱

Fig.22Coherenceandphasefunctionsfromcross-spectraofthepressurebetweensamplingpointsfromD6toG6andtheircorrespondingpointsfromH6toK6

a 互谱

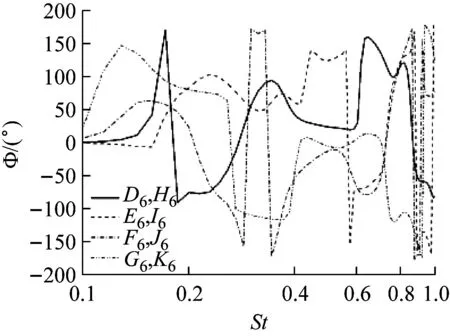
b 相谱图23 D6～G6与L6～O6对应测点压力互谱与相谱

Fig.23Coherenceandphasefunctionsfromcross-spectraofthepressurebetweensamplingpointsfromD6toG6andtheircorrespondingpointsfromL6toO6

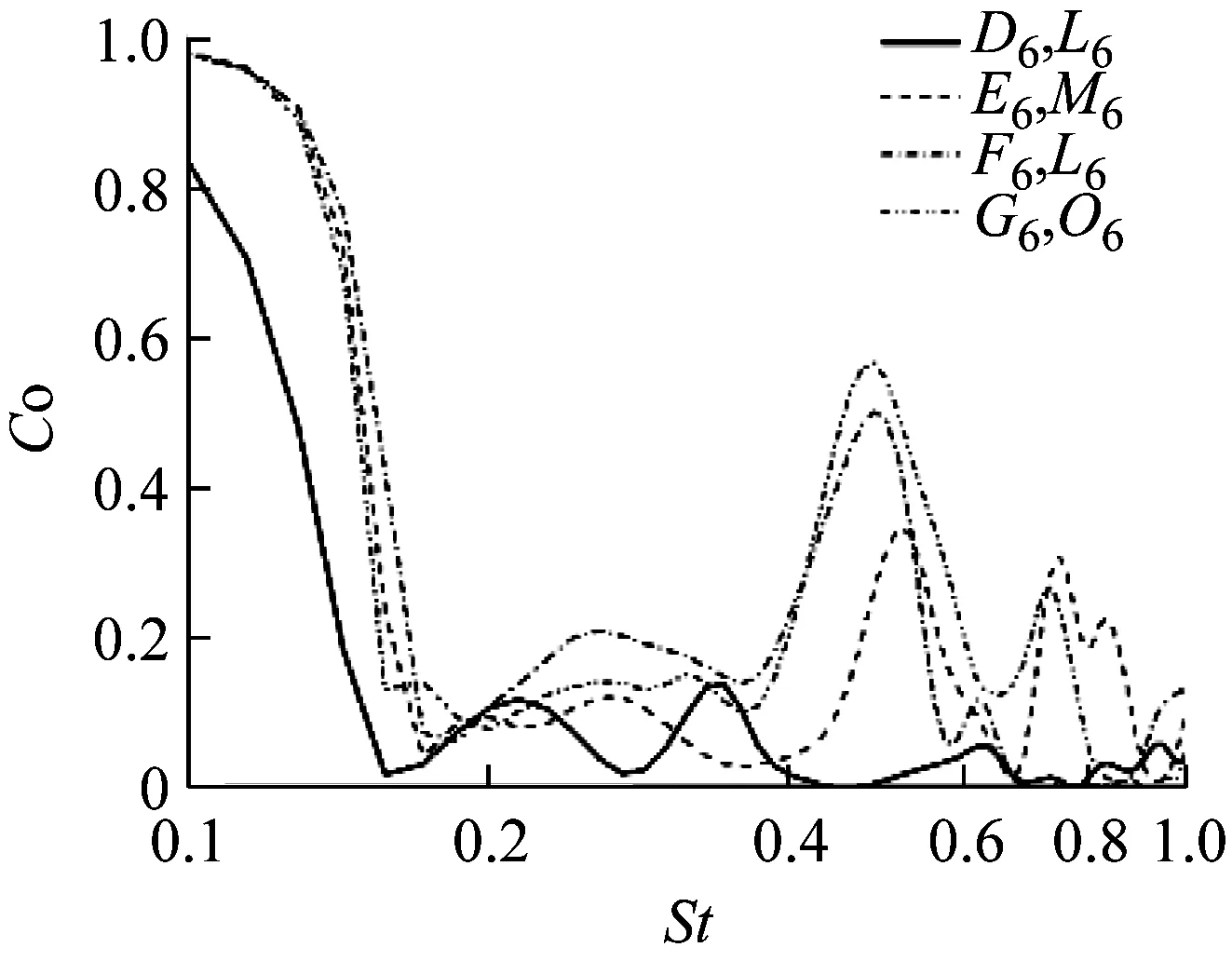
a 互谱

b 相谱图24 D6～G6与L6～O6对应测点X向速度互谱与相谱

Fig.24Coherenceandphasefunctionsfromcross-spectraoftheX-velocitybetweensamplingpointsfromD6toG6andtheircorrespondingpointsfromH6toK6

a 互谱

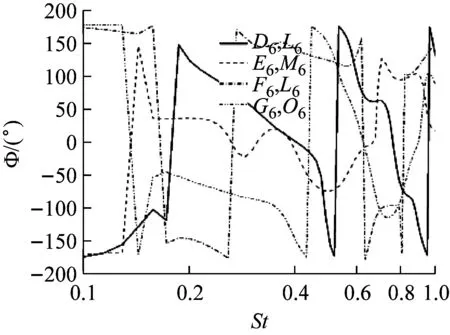
b 相谱图25 D6～G6与L6～O6对应测点Y向速度互谱与相谱

Fig.25Coherenceandphasefunctionsfromcross-spectraoftheY-velocitybetweensamplingpointsfromD6toG6andtheircorrespondingpointsfromH6toK6

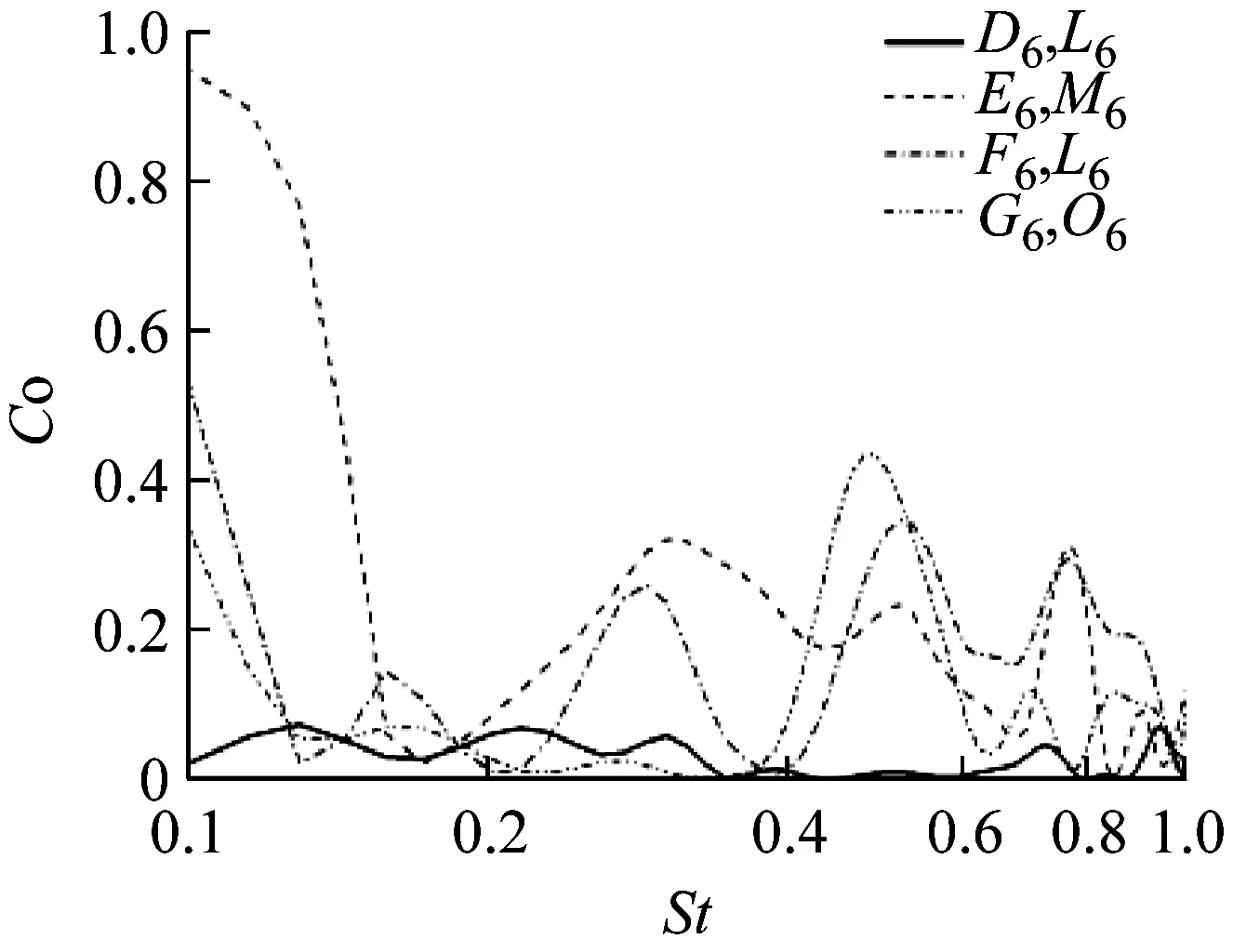
a 互谱

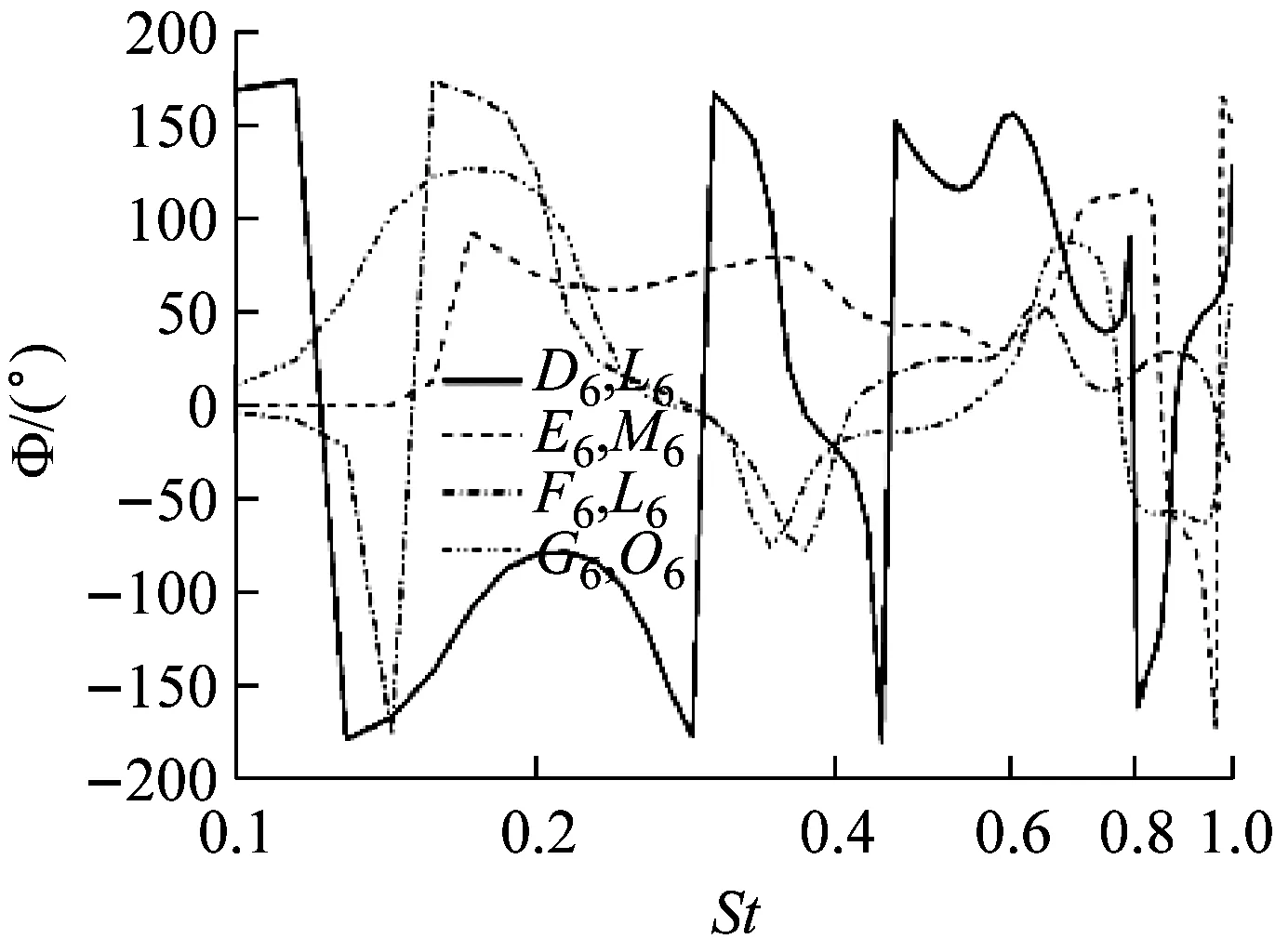
b 相谱图26 D6～G6与L6～O6对应测点Z向速度互谱与相谱

Fig.26Coherenceandphasefunctionsfromcross-spectraoftheZ-velocitybetweensamplingpointsfromD6toG6andtheircorrespondingpointsfromH6toK6

图27 H～K列测点压力功率谱Fig.27 PSD of the pressure at sampling points from H-series to K-series

图28显示了H～K列上、下侧对应测点的压力互谱与相谱分析结果.H～J列互谱在特征频率Stb=0.49时具有高度或中度相关性，且在相谱上存在180°相位差，表明上、下侧展向涡呈现类似卡门涡街交替产生并脱落的过程.当到达流向位置K时，相关性有一定程度地减弱，且相谱上存在既非0°又非180°的相位差，证实了上侧展向涡比下侧展向涡耗散得更快的结论.