串联机器人多模式标定与刚柔耦合误差补偿方法研究

陈宵燕 张秋菊 孙沂琳

(1.江南大学机械工程学院， 无锡 214122； 2.江苏省食品先进制造装备与技术重点实验室， 无锡 214122)

0 引言

随着工业机器人在诸多领域的优势越发明显[1-2]，促使其不断地向着离线复杂任务编程、高精度且大范围运动的方向发展，同时，工业机器人绝对定位精度较低的问题也愈加突出[3]。机器人绝对定位精度误差主要是几何误差与非几何误差[4-5](主要由自重和负载引起的连杆及关节变形)。

目前提高机器人精度的方法可分为标定和补偿两种，前者应用较成熟，且一般仅对运动学模型标定[6-8]。针对目前串联机器人发展应用的短板，需同时考虑多种误差对机器人定位精度的影响，尤其是非几何误差问题亟需解决。一般工业机器人连杆刚度较高，在负载及速度较小的情况下，可忽略连杆柔性因素所带来的连杆长度变化，而其导致的关节角微小变化可以映射到关节变形上[9-10]。此外，关节变形主要是由传动件产生，较之连杆偏大，且引起的角度误差具有放大效果，导致其产生的定位误差无法忽略[11-15]。对于上述非几何因素的影响，依靠机器人标定技术是无法消除的，因此误差离线补偿成为提高机器人精度的重要手段之一。

本文将针对上述问题，分析几何误差和关节柔性误差对工业串联机器人绝对定位精度的影响。首先，建立几何误差与关节柔性误差因素相结合的误差模型，并提出一种改进的非线性辨识算法实现稳定辨识。此外，考虑测量环境的外部约束影响，提出一种智能选取测量位姿的测量优化方法。最后，综合多种精度提高方法形成一种多模式精度提高策略，并基于Matlab高级矩阵/阵列语言，结合GUI人机交互界面等优势[16]，完成机器人多模式快速标定及误差离线补偿系统的开发及实验验证，从而提高机器人绝对定位精度。

1 误差模型

运动学误差模型主要是基于HAYATI等提出的修正的5参数MDH方法，其考虑了DH 模型存在参数不连续的缺点[17]。MDH方法是在DH模型的基础上，引入附加转动项Rot(yi,βi)，连杆变换关系为

Ai=Rot(zi-1,θi)Trans(0,0,di)
Trans(ai,0,0)Rot(xi,αi)Rot(yi,βi)

(1)

参照文献[18]，采用微分法建立机器人运动学误差模型，对式(1)进行全微分，可得微分方程

(2)

采用误差参数向量Δθ、Δd、Δa、Δα和Δβ来表示机器人关节角度偏移、连杆长度偏差、连杆偏移、扭角偏差和相邻平行关节偏移。此外，在测量过程中，机器人基坐标系无法直接测量，通常使用间接测量法获得构造基坐标系。由于构造方法及测量误差导致构造基坐标系与实际基坐标系存在微小偏移，本文使用一个变换矩阵BT0来代表机器坐标系的偏移量，其含有6个误差参数变量(Δσ)。最终，可得到初始机器人运动学误差模型为

(3)

基于全微分方法，展开式(3)，并从dTR中提取位置误差部分。当机器人为一般6自由度串联机器人时，为30-参模型(6个机器人零位关节角度变量、5个连杆长度变量、6个连杆偏移变量、6个扭角变量、1个平行度变量、6个基坐标系偏移变量)，获得的机器人完整运动学位置误差模型为

ΔXk=Hkηk

(4)

其中

Hk=Mθ+Md+Ma+Mα+Mβ+Mσ

(5)

(6)

式中 ΔXk——几何误差导致的机器人位置误差

Hk——运动学误差模型的辨识矩阵

ηk——运动学误差参数集

Mθ、Md、Ma、Mα、Mβ、Mσ——系数矩阵

根据文献[19]，针对负载对关节变形量的影响，采用基于线性扭转弹簧的建模方法，对于一般6轴串联型机器人，根据平衡力矩与微分变形转换到机器人末端位置误差为

(7)

针对连杆自重的影响及一般6自由度串联型机器人只需考虑关节2、3的变形量，因此机器人在连杆自重影响下产生的位置误差为

(8)

综上所述，结合机器人几何误差与负载及连杆自重引起的柔性误差，当机器人为一般6轴串联机器人时，为39-参模型(30-参模型对应误差参数，加上6个关节柔性变量以及3个连杆自重参数变量)，建立的机器人完整刚柔耦合位置误差模型为

(9)

式中H——耦合误差模型的辨识矩阵

ΔX——几何误差和关节柔性误差导致的机器人位置误差

Δη——完整耦合误差参数集

2 精度提高策略

在获得上述完整运动学位置误差模型或者刚柔耦合位置误差模型后，通常采用QR分解并分析得到无冗余的机器人参数辨识矩阵，该矩阵所对应的参数即为可辨识误差参数集。为获得准确的误差参数值，可靠且高效的辨识算法和测量方法是必不可少的。

2.1 非线性辨识方法

通常采用最小二乘法来辨识机器人系统误差参数，该损失函数为

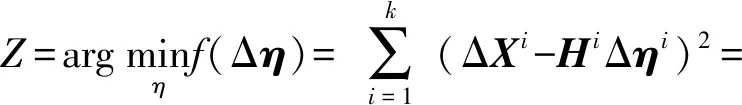
(10)

在实际应用中，由于机器人误差是非线性的，直接使用最小二乘法辨识的参数不具备稳定性。梯度下降法属于一阶收敛，当给定一个参数向量时，算法根据函数值下降最快的方向调整参数向量，在若干次迭代之后找到局部最小。梯度下降法的缺点是接近最优值时收敛速度变慢，并且对初始点的选择极为敏感，易陷入局部最优。Gauss-Newton法属于二阶收敛，因此相对梯度下降法收敛速度快，从而避免了前者局部最优的问题，具有全局寻优的性能。但是Gauss-Newton法在迭代稳定性上略有弊端。因此，本文采用一种基于残余误差ΔX的改进的Lveveberg-Mavquardt算法(M-LMA)。当函数下降过快时，使用较小的参数，调节M-LMA更接近高斯牛顿法。当函数下降太慢时，则使用较大的参数，调节M-LMA更接近梯度下降法，从而提高其收敛速度和参数辨识精度。此外，为使调节步长参数更加适应辨识函数的特性，将调节步长参数的变化因子与残余误差ΔX相结合，决定参数辨识算法的步长。本文提出的误差辨识算法为

Δη=(HTH+β(ΔX)I)-1HTΔX

(11)

其中

(12)

式中υ——调节因子

M-LMA算法对υ敏感度不高，可取4≤υ≤100，本文取υ=10。

由于机器人测量时存在随机干扰误差，为了进一步提高辨识精度，通常在测量时重复多次测量，将每组数据都通过M-LMA得到辨识结果，并将所对应的预测残差经加权递推平均滤波算法进行筛选，得到对应的辨识参数，并对其求均值优化最终获得辨识结果。

2.2 智能选取优化方法

为获得机器人运动学误差模型和位置耦合模型所对应的正确误差参数值，除了稳定高效的辨识方法之外，可靠有效地测量位姿对象也必不可少。由于机器人运行时存在测量扰动，一般测量位姿点数越多，误差参数值的辨识准确度越高。由文献[19]可知，只要取得适当的测量位姿，参数辨识精度将不再随着测量点数的增加而提高，而这个临界点，通常作为最小最优测量点数。同时，不同空间位置和不同姿态方向都会影响误差参数的辨识[20-21]。在机器人校准领域中，都将辨识雅可比矩阵的奇异值作为目标函数求得最优解。然而这些算法都忽略了测量仪器、机器人末端执行器和机器人本身结构对测量位姿选取的影响。

本文考虑了测量设备检测特性及末端执行器几何特性对测量位姿智能选取的外部约束影响，并以可观性指数因素O1为主要目标函数。然而，研究发现当可观测性指标取得最优时，也会出现辨识精度较差的结果。因此，本文结合机器人模型误差参数预测辨识精度指标为寻优成功的决策条件，最终提出一种LDW-PSOA测量优化方法。粒子群优化(PSO)算法是一种基于群体智能的进化计算方法，它与遗传算法相似，具有搜索速度快、高维适应性强、内存容量大、结构简单、易于工程实现等优点。线性递减权重因子可对于平衡算法的全局搜索能力和局部改良能力具有关键作用，较小的惯性权重能提高算法局部搜索能力和较大的惯性权重能使算法更好地体现全局搜索能力。首先，通过奇异值分解，式(9)转换为

ΔX=UΣV′Δη+ξ

(13)

其中

(14)

式中U、V′——正交矩阵

Σ——对角矩阵，Σ由奇异值(σi)构成，其中奇异值(σi)以递减序列排列

ξ——扰动残余误差

可观性指数O1由奇异值计算可得

(15)

LDW-PSOA的惯性权重因子w的计算公式为

(16)

式中wmax、wmin——w的最大值和最小值

tmax——最大迭代步数

t——当前迭代步数

LDW-PSOA的目标函数为

minf=Omin(f(σ))-1

(17)

其中Omin=γ1[∑(Δθi-Δθi,real)2+

(18)

式中Omin——辨识精度指标

γ1、γ2、γ3、γ4——权重系数

当目标函数取得最优时，将获得的一组最优测量位姿进行参数辨识。当可观测性指标取得最优时，利用Matlab仿真分析得到预测辨识结果进行判别，若辨识精度达到96%以上，则程序可判定目标函数寻优成功，反之，则程序重新寻优，直至找到一组目标最优测量位姿。

本文提出的智能选取测量位姿方法可以确定一组最优机器人测量位姿，这些位姿点可以使测量扰动引起的偏差减到最小且达到最佳辨识精度(适合的测量位姿点数及满足需求的辨识精度)，且满足了测量设备检测特性及末端执行器几何特性的约束要求。因此，该方法不仅可以提高测量过程的效率，且对辨识的正确性和稳定性有着较大的提升。

2.3 精度提高方法

在获得机器人待测量位姿点后，获得机器人基坐标系及参考坐标系，是机器人标定和补偿方法应用所需面临的实际问题。结合工程实际，本文采用任意用户坐标系作为参考坐标系的方法来构建机器人基坐标系。当机器人状态为标定前，由于其存在结构误差和随机误差等因素，构建的用户坐标系与实际存在误差，即以此构建的基坐标系与实际的基坐标系存在误差(Δσ)。在后续操作为标定时，由于MDH参数已校准，用户坐标系原点所对应的关节值改变，使其构建的基坐标系得到校准，因而不需要修改Δσ所指参数。若后续操作为补偿时，误差Δσ将会直接修正补偿值。

本文提出的离线补偿方法，包含全局补偿模型和局部精补偿模型。全局补偿模型对机器人工作空间的任意位置、任意姿态都具备可靠有效的离线补偿优化功能。局部精补偿模型只能对某一姿态或某一方向进行高精度补偿。在参数标定和离线补偿的误差模型选择上，结合机器人自身特性及加工需求，提出了一种基于辨识精度和预测残差的模型择优方法。在获得用于参数标定或补偿模型建立的实际测量位置后，确定对应最大无冗余误差模型及最小误差模型，以其对应误差参数差值n为对象，进行组合。若最大误差参数为27个，最小为13个，其组合对应的模型有16 383种，计算公式为

(19)

式中m——从差值中选取的数量

阈值是根据加工所需的定位精度及模型的预测精度均值给定。当模型预测精度满足加工所需最低定位精度，且大于整体预测精度均值的95%时，选出所有满足阈值的模型对象。最后，利用预测精度及参数数量排序寻优，从中获得最佳模型

Ψmax=max(κ1ξi+κ2Δηi)

(20)

式中κ1、κ2——权重系数，取κ1=50，κ2=0.05

本文所提出的多模式精度提高策略，可根据机器人型号选定不同的标定和补偿模型，并根据加工需求选择机器人标定、全局补偿及局部精补偿3种不同方法的最佳组合。这种精度提高策略为改善机器人定位精度提供了灵活便捷且高效可靠的解决方法。

3 实验与结果

机器人标定与补偿实验对象为Staubli Rx160L机器人，额定负载为14 kg，工作半径为2 010 mm。该机器人为6自由度串联机器人，并且初始状态为使用拆装后未经标定的，因此绝对定位精度较差。测量仪器为Faro激光动态跟踪仪，具有测量精度高(分辨率0.5 μm，精度8 μm+0.4 μm/m)，测量范围大(直径160 m)，调整安装方便，具有很好的柔性和可操作性等优点。机器人标定和离线补偿实验平台如图1所示。

图1 机器人标定和离线补偿实验平台Fig.1 Experimental platform for robot calibration and off-line compensation1.Staubli Rx160L机器人 2.计算机及数据测量配套软件 3.Faro激光动态跟踪仪

3.1 机器人标定与全局补偿

为了验证本文提出的机器人标定和全局补偿方法的有效性，根据该机器人的结构特性及基于第1节建立的30-参模型，结合QR方法，利用择优方法选择20-参模型来获取机器人实际DH参数。同时，基于第1节建立的39-参模型，择优选择35-参模型作为机器人全局补偿模型。

为提高机器人标定及补偿模型的有效性和稳定性，根据提出的LDW-PSOA获得最佳的一组机器人测量位姿。为了平衡测量效率和模型准确度，选择50个点作为本次实验最优的测量点数。因此，LDW-PSOA的维度为50，种群的大小为500(种群越大，算法全局性能更优)。实验利用名义用户坐标系(1 200,-500,-250,180,0,-90)来构建机器人基坐标系，用户坐标系的Z轴方向与机器人基坐标系Z轴方向相反，Y轴方向与基坐标系X轴方向相同。利用上述20-参标定模型和35-参全局补偿模型，通过LDW-PSOA获得一组最优测量位姿点，并通过Faro激光跟踪仪测量获得实际值。根据提出的非线性辨识方法，计算得到机器人实际MDH参数如表1所示。校准参数时，实际只需修正机器人控制器中16个DH参数， Δσ不需要修改。

表1 Staubli Rx160L机器人修正后的MDH参数Tab.1 Modified MDH parameters of Staubli Rx160L robot

为了验证校准参数和补偿模型的准确性及有效性，在机器人工作空间内任意选取40个位姿点作为验证点。首先利用目标位姿名义值，在原MDH参数模型下运行机器人，测量得该40个位姿点的初始实际值，从而获得初始误差。然后仍使用目标位姿名义值，在校准后的MDH参数模型下，测量得该40个位姿点的实际值，从而获得标定后的残余误差。

对于全局补偿方法，需将目标位姿名义值经过全局补偿，获得中间位姿名义值，将其输入机器人控制器，在原MDH参数模型下运行机器人，测量得该40个点的实际值，从而获得全局补偿后的残余误差。表2给出了机器人标定和全局补偿前后的实验结果，表明了标定及全局补偿对精度的提高都有明显的效果。此外，根据表2中定位精度平均值可知，参数标定后精度提高了95.75%，全局补偿后精度提高了97.27%，因此后者的提高效果更加显著。

表2 机器人标定和全局补偿前后的定位精度Tab.2 Positioning accuracy before and after robot calibration and global compensation mm

3.2 机器人局部精补偿

对于某些机器人应用场合，如Staubli Tx/Rx系列机器人在激光切割领域的应用，加工任务中对激光切割头在竖直方向上的精度要求远大于其他方向。因此，在机器人本身性能未能达到要求，且加工范围大并具有较大负载时，需要对机器人在竖直方向上作进一步的离线补偿优化。

机器人运动姿态一般用欧拉角表示(绕轴x、y、z的旋转序列)，根据旋转序列获得旋转矩阵

(21)

机器人工具坐标系所指方向通常指接近矢量a，根据式(21)可知，绕工具坐标系z轴转φ只影响方向矢量n和法线矢量o，与接近矢量a无关。因此，针对机器人工具坐标系某一矢量方向，可分为两种情况，一种是固定姿态(旋转矩阵完全相同)，另一种是任意φ角的固定矢量方向(接近矢量a相同，方向矢量n和法线矢量o任意)。

对于第1种情况，可直接采用全局补偿方法一步获得高精度定位精度。选择竖直方向为实验矢量方向，在用户坐标系下，选择机器人固定姿态为(0,0,90)。首先根据Matlab仿真及蒙特卡洛法，模拟固定姿态点，并基于本文建立的39-参模型，利用择优方法选择24-参模型作为机器人局部精补偿模型。同时，结合LDW-PSOA，在该固定姿态下智能选取50个测量位姿点，确立机器人局部精补偿模型。最后，在机器人工作空间内选择均布点阵525个位姿点，经过局部精补偿优化，获得局部精补偿后的残余误差。由表3可知，机器人残余误差最大值从补偿前10.55 mm降为补偿后0.26 mm，平均值从补偿前9.55 mm降为补偿后0.12 mm，平均精度提高率为98.7%。

表3 机器人固定姿态下全局补偿前后的定位精度Tab.3 Positioning accuracy before and after global compensation for robot with constant orientation mm

对于第2种情况，有两种精度提高模式，一种是校准参数后再进行局部精补偿，另一种为全局补偿后再进行局部精补偿。首先，选择竖直方向为实验矢量方向，选择5组姿态为(-2.000 3, -0.999 4, 178.965 1; -2.000 3, -0.999 4, 133.965 1;-2.000 3, -0.999 4, 91.965 1; -2.000 3, -0.999 4, 40.965 1; -2.000 3, -0.999 4, 0.965 1)。根据上述方法，利用建立的39-参模型，择优选择29-参模型作为机器人局部精补偿模型。同时，根据所提出的算法，在该固定姿态下智能选取100个测量位姿点(每组20个位姿点)来确立机器人局部精补偿模型。最后，在机器人工作空间内选择接近上述5组姿态方向的均布点阵384个位姿点，重复上述操作，获得局部精补偿后残差，实验结果见表4。

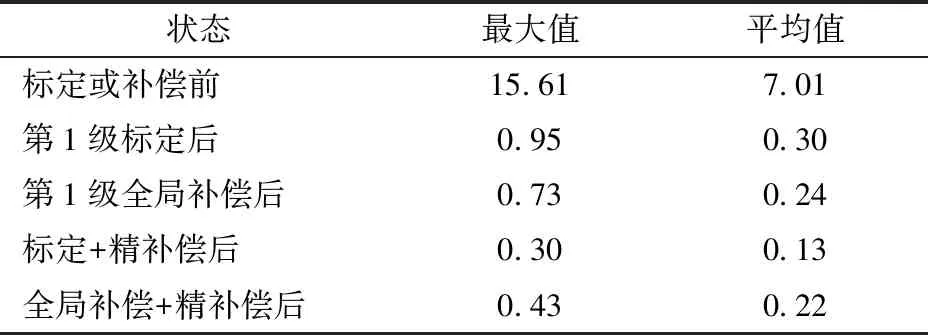
表4 多模式精度提高前后的残余误差Tab.4 Residual errors before and after multi-mode accuracy improvement mm

从表4可知，多模式精度提高策略的第1级为机器人标定或全局补偿，其使得机器人定位误差均值从初始7.01 mm降为标定后0.30 mm和补偿后0.24 mm，显然提高率都非常显著。此外，作为第2级的局部精补偿方法对于标定后或全局补偿后机器人精度的进一步提高也都有着较为明显的效果，尤其是残差最大值，前者使其从0.95 mm降至0.30 mm，后者则从0.73 mm降至0.43 mm。

为了进一步验证该局部精补偿模型在任意转角φ下都具有精度改善效果，设计了对比实验。任意选择在竖直方向上的5个不同转角φ，其姿态为(-1.049 6, 0.929 7, 96.321 3; -5.473 7, -5.262 8, 173.634 8; -8.025 2, -3.430 7, 43.340 9; -2.000 5, -0.999 0, -21.113 9; 0.013 8, -9.135 5, 122.834 3)。最后，在机器人工作空间内选择该5组姿态方向的均布点阵384个位姿点，基于上一个实验确立的局部精补偿模型。重复上述操作，获得局部精补偿后的残余误差，实验结果如表5所示。

表5 机器人任意转角下局部精补偿后的残余误差Tab.5 Residual errors after local precise compensation for robot with arbitrary angle mm

可验证这个由原5组姿态建立的29-参局部精补偿模型，在该竖直方向的任意转角φ及任意工作空间下，对机器人绝对定位精度进一步提高有着较好的有效性和可靠性。此外，从第2种情况的两个实验结果可知，机器人标定与局部精补偿相组合的模式对精度提高的效果优越于本文其他精度提高方法。

3.3 GUI交互系统

将上述建立的机器人误差模型(30-参机器人运动学误差模型和39-参机器人刚柔耦合位置误差模型)，以及提出的改进辨识算法(M-LMA)、优化的智能选取算法(LDW-PSOA)与多模式精度提高方法集成到软件中。基于Matlab开发平台，利用其数值分析、计算等高级计算语言，结合GUI人机交互界面技术，开发了机器人标定及离线优化系统，运行后的界面如图2所示。

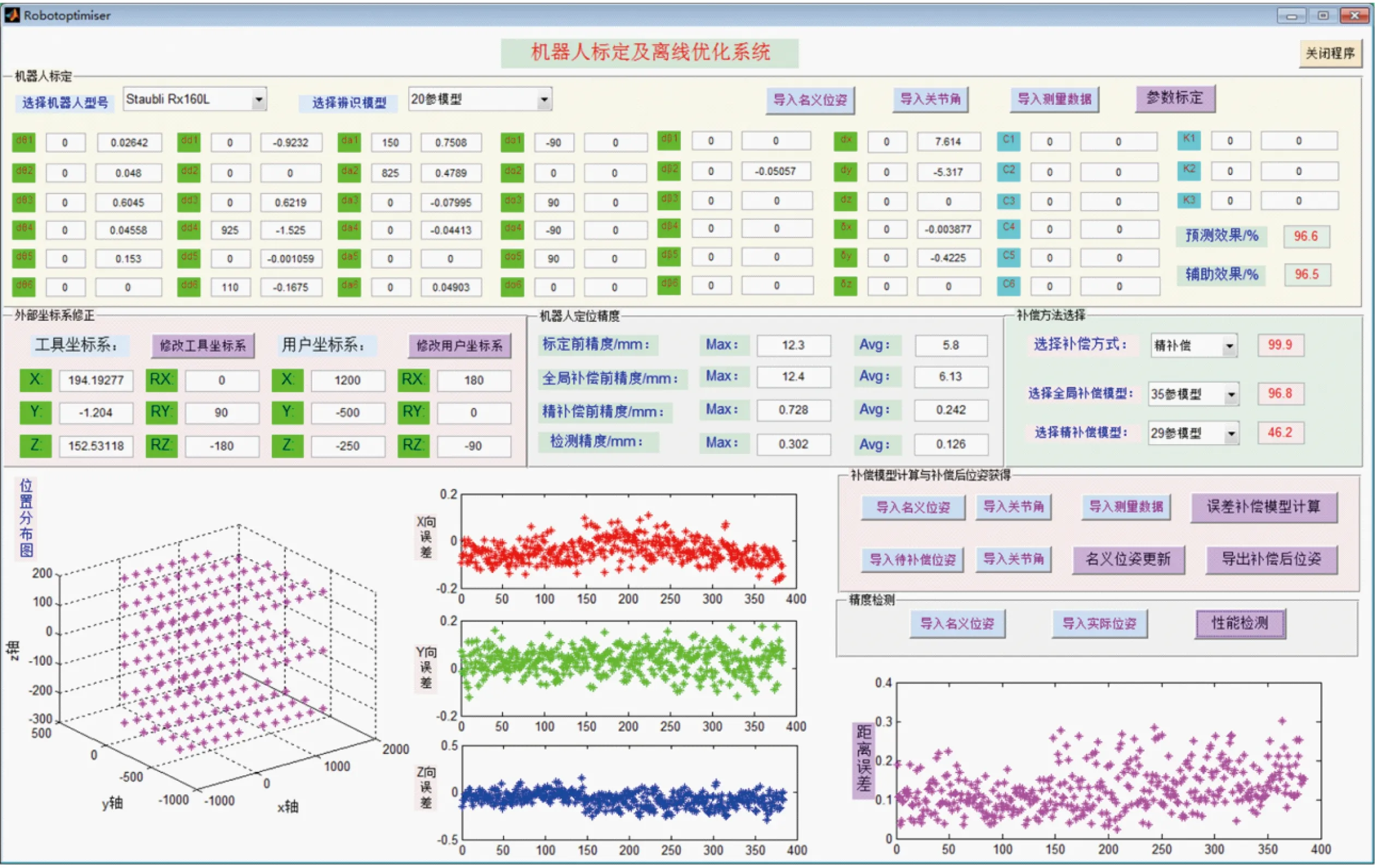
图2 机器人标定及离线优化系统GUI界面Fig.2 GUI interface of robot calibration and off-line optimisation system

系统可根据实际需求增加机器人型号，并具有多种标定及补偿模型可供选择，利用预测效果比较，择优选择最合适的模型。现已有机器人型号为Rx160系列、Tx60系列、Tx90系列。

4 结论

(1)建立了几何参数误差与外负载和连杆自重引起的关节柔性误差相结合的刚柔耦合位置误差模型。

(2)基于残余误差和加权递推平均滤波算法，提出了一种M-LMA来稳定辨识多种误差模型对应的误差参数。

(3)考虑了外部约束条件，以参数辨识精度指标Omin和可观性指数O1为目标函数，提出了一种基于LDW-PSOA的测量位姿智能选取方法。

(4)提出了一种局部精补偿方法，其可分别与参数标定及全局补偿方法同时使用或者直接单独应用，从而形成了较为完善的多模式精度提高策略。

(5)利用开发的系统，对Staubli Rx160L机器人进行了多模式精度提高实验，在5组不同姿态下对384个点位的测试，首先利用标定方法使最大定位误差从标定或补偿前的15.61 mm降为0.95 mm，而基于全局补偿法则降至0.73 mm；利用标定结果结合局部精补偿，残差最大值降为0.30 mm，而利用全局补偿结果结合局部精补偿，残差最大值则降至0.43 mm。