一种改进的K-means算法在城市通勤研究中的应用
2019-04-01周天绮杨志民
周天绮 杨志民
1(浙江医药高等专科学校医疗器械学院 浙江 宁波 315100)2(浙江工业大学之江学院 浙江 杭州 310024)
0 引 言
通勤指的是从业人员离开居住地前往工作地的出行活动,可反映一个城市中劳动力的活动半径[1]。通勤发生于就业人口中,受职住空间分布结构的影响。通过聚类分析居住与就业集聚地可以描绘出城市居民出行的时空特性,统计空间单元的通勤属性,由此反映城市的空间结构[1]。
1 算法设计
K-means聚类算法是属于划分方法中的基于质心技术的一种方法。划分的思路是以k为参数,把n个数据样本划分为k个类,以使生成的每个聚类(又称簇)类内紧凑,类间独立。
1.1 聚类性能评价
聚类是根据数据对象之间的相似程度来划分类的,相似程度是用对象之间的距离来衡量的,一般采用的是欧式距离。假设给定的数据集X={xm|m=1,2,…,ntotal},X中的样本有d个属性(维度)A1,A2,…,Ad[3],则欧式距离公式如下:
(1)
d(xi,xj)距离越小,样本xi和xj越相似,差异度越小[3];反之,样本xi和xj越不相似,差异度越大[3]。
K-means聚类算法使用误差平方和准则函数来评价聚类性能[3]。给定数据集X,包含k个聚类子集X1,X2,…,Xk[4];各个聚类子集的质心分别为m1,m2,…,mk。误差平方和准则函数公式为[4]:
(2)
E函数表示每个样本点到其质心的距离平方和[4]。算法需将E调整到最小使各聚类达到最优。
1.2 算法流程
K-means聚类算法具体流程如下:
输入:簇的数目k和包含m个数据样本的数据集X={xm|m=1,2,…,ntotal},每个xi∈Rd,d为数据纬度。
输出:k个簇C1,C2,…,Ck, 使平方误差准则最小。
① 随机选取k个聚类质心:m1,m2,…,mk[5]。
② 重复下面过程直到收敛[5]。
{
对于每一个样例xi,按下式计算其应该属于的类[5]:
(3)
对于每一个类j,按下式重新计算该类的质心:
(4)
}
k是预先选定的聚类数,ci代表样例xi到k个类的质心距离最近的那个类。mj为一个类的质心,其初始值是随机选取的。算法过程描述如下:① 在数据集中随机选取k个对象作为k个类的质心;② 对于数据集中的每个对象分别计算其到k个质心点的距离,然后选取距离最近的那个类作为ci,这样每一个对象都有归属的类[6];③ 对于每一个聚类,对类中所有的数据点求均值,重新计算它的质心mj;④ 重复迭代②和③直到质心不变。
1.3 算法缺点
对处理大数据集来说,K-means算法是相对可伸缩和高效率的。但缺点也比较明显:
(1) 必须事先设定k值,而且对聚类质心的初始值敏感,对于不同的初始值,可能会导致不同的聚类结果,经常会发生得到局部最优解的情况。
(2) 对于“躁声”和孤立点数据是敏感的,少量的该类数据就能对聚类质心和聚类结果产生极大的影响[8]。
1.4 算法改进
1.4.1 采用类间相异度确定k值
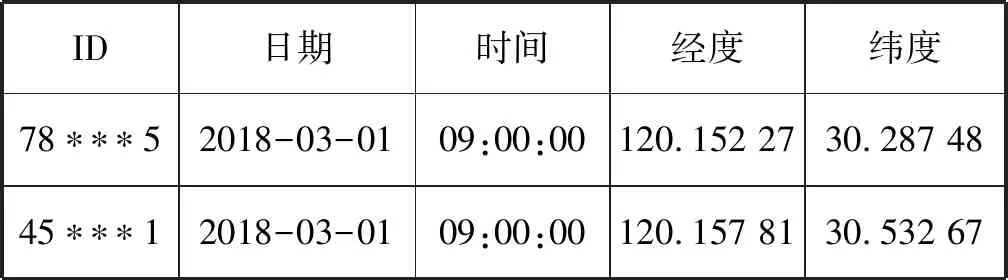
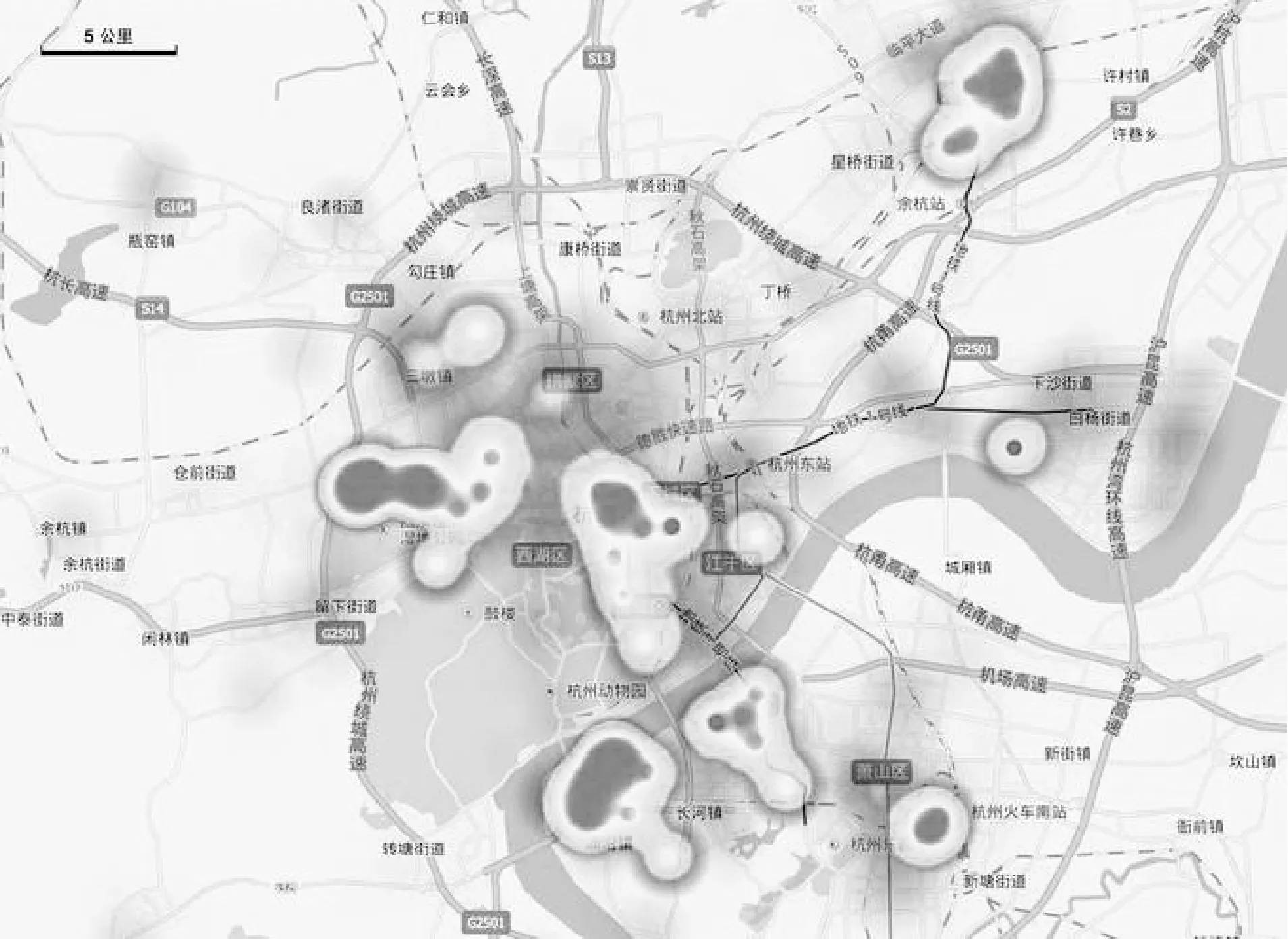
利用类间相异度来确定最终的k值。思路如下:① 初始化聚类质心:计算所有样本的平均值作为数据集的中间点m0,利用欧式距离公式找出距离中间点m0最远的对象m1,再找出与m1距离最远的对象m2,选取m0、m1、m2作为初始聚类的质心。② 计算其他对象到每一个质心点的距离,取最小距离D,计算质心点之间的距离,取最小距离C,如果D 类间相异度DCA计算公式如下: (5) 式中:kt表示当前聚类的个数,mi、mj分别为类Ci和Cj的质心,d(mi,mj)表示类Ci和Cj的欧式距离。 改进后的算法描述如下: (2) 计算剩余对象到各质心的欧式距离,选择距离最近的质心归类,重新计算各聚类质心。 (3) 计算剩余对象到质心的最小距离D及质心之间的最小距离C,并计算出类间相异度DCA_o。 (4) 如果D>C,则把该对象作为备选质心点,重新计算类间相异度DCA_n,运行步骤(5),否则转到步骤(6)。 (5) 如果DCA_n>DCA_o,则把该对象作为新的质心,生成新类,此时k=k+1,重复迭代步骤(2)-步骤(5),否则保持原态,执行步骤(6)。 (6) 取下一个类Ci,如果没有新的类,转到步骤(7),否则重复迭代步骤(2)-步骤(5)。 (7) 输出各个聚类:C1,C2,…,Ck。 1.4.2 消除噪声和孤立点的影响 通过改进原始算法找出数据集中的噪声和孤立点进行消除。对于数据集X={xm|m=1,2,…,ntotal}中的每一个对象xi,计算其与剩余对象的距离和Si,另外计算出所有对象的距离均和H,如果Si>H,则xi被认为是孤立点,予以删除。公式如下: (6) (7) 本次实验数据选取杭州移动公司提供的手机通信数据。按照触发手机定位的方式,手机定位数据可分为主动方式(主叫、被叫、短信、位置区切换)和被动方式(定时扫描)[9]。被动方式是GSM通信系统通过定时扫描周期性地更新手机用户的位置信息[9]。由于被动方式触发周期约为55 min,具有获取数据完整且稳定的优点[9],本次研究采用被动方式触发的手机定位数据。 首先需要对数据进行清洗,删除无效和冗余数据。其次,还需删除手机号码等用户私密信息,用户ID可采用加密后的IMSI号表示[10]。数据预处理流程如下: (1) 从原始数据中提取被动方式触发的手机定位数据,包括定位的时间和位置信息(经纬度坐标)。 (2) 分别建立工作时段和夜间睡眠时段的手机定位信息数据表。设置工作和夜间睡眠时段,根据居民作息时间,设置工作时段为09:00-17:00,睡眠时段为23:00-次日06:00。筛选出相应时段的手机定位数据存入对应的数据表。 经处理后的手机定位数据表格式如表1所示。 表1 手机定位数据表格式 本次实验采用python语言分别实现K-means算法和改进后的K-means算法。在相同的实验环境下对两种算法在职住锚点分析中的聚类效果和运行效率进行分析比对。具体实验环境:Arch Linux+ArcGIS 10.5.1+Python 3.7+Pycharm+Matplot。 为了客观比较两种算法的性能,从工作时段的手机定位数据表中随机选取100个定位点进行工作地锚点聚类实验,将手机定位数据映射到杭州市行政区划图,具体数据点分布如图1所示。 图1 测试数据分布 2.3.1 K-means算法实验分析 K-means算法需要预先设定k值,实验中k取4,即随机选取4个质心点。整个聚类过程如图2所示。图中每一种颜色代表一个簇,圆点表示样本点,代表手机用户所在的位置;正方形表示聚类质心,代表工作点锚点。 K-means算法经过8次迭代实现收敛。由于聚类质心是随机选择的,陷入局部最优的概率较大。图2中第一次迭代初始质心选在了同一个类中,导致迭代次数过多,甚至可能因出现局部最优导致错误的聚类,这是K-means算法中比较明显的缺点。 噪声点影响分析:由于K-means算法不能识别噪声点,少量的噪声点就能使聚类质心产生偏移。图2中最后一次迭代蓝色代表的簇,其质心相对于聚集点群往边上偏移,据分析是受到右边数据点的影响。 2.3.2 改进的K-means算法实验分析 为了克服K-means算法对初始质心依赖较大的缺点[4],应尽可能地将聚类质心均匀分散在整个数据集上,避免陷入局部最优,同时也可以降低K-means算法的迭代次数,提高收敛速度。 改进的K-means算法通过选取数据集的中心点m0、离中心点最远的点m1及离m1最远的点m2作为初始质心,并通过类间相异度的计算迭代确定k值。聚类过程如图3所示。 改进的K-means算法经过3次迭代快速实现收敛,因为预先对初始聚类质心进行了优化,避免了K-means算法中出现的局部最优问题。另外,按照1.4节介绍的方法找到噪声点并予以删除,图3中用“×”标注被删除的噪声点。从图3的最后一次迭代可看出四个簇的质心均在聚集点群,未受到噪声点的影响。 居住地聚类分析实验也得到了上述相同的结果。由此得出:改进的K-means算法可有效避免初始化聚类中心引起的局部最优问题,消除噪声和孤立点对聚类结果的影响。 本次研究数据由中国移动杭州分公司提供,选取了2018年3月份的手机通信数据,按照上文介绍的方法对数据进行预处理,建立如表1所示的工作时段和夜间睡眠时段的手机定位数据表。 将杭州市行政区划图和分街道地图矢量化,并进行地图匹配和几何校正[10]。对GIS矢量数据图层进行坐标转换,使得手机定位数据坐标系与地图矢量数据一致[10],将手机定位数据映射到城市矢量地图中。 使用ArcGIS将手机用户位置坐标转化为杭州市手机用户空间点数据文件。研究范围定为杭州市,涵盖萧山、余杭、临平、富阳,不包括其他县市。点空间数据准确标明了手机用户在城市空间中的地理位置,以此作为空间聚类的基础,能够更加真实地反映城市人口职住地的聚集。 职住平衡指的是城市中某个空间单元内,居民人口数量和就业岗位数量大致相等,大部分居民可以就近工作,通勤交通采用步行或自行车,通勤距离和时间也较短[11]。度量指标一般采用职住比,即在某个空间单元内就业岗位数量与居民人口数量之比[1]。职住比越大,表示该空间单元倾向就业,反之倾向居住。当职住比介于0.8~1.2之间时,认为是平衡的。 某空间单元内职住比的计算按以下过程进行处理:① 按用户进行分组排序。② 统计出样本中每一个用户在工作时段和夜间睡眠时段出现次数最多的定位数据作为用户当天的工作地锚点和居住地锚点。③ 通过改进的K-means算法对样本中所有用户的工作地锚点和居住地锚点分别进行聚类分析,得到居住地和工作地聚类。对于跨空间单元的聚类,聚类质心位于某个空间单元内,就认为是该空间单元的聚类。④ 在聚类中删除用户ID相同的多个定位点,只保留离质心最近的定位点,这样聚类中样本数与手机用户数一致。⑤ 利用空间单元内工作地聚类中的手机用户数占居住地聚类中的手机用户数的比值来计算职住比。 某空间单元内职住比的计算公式如下: (8) 杭州市各个行政区职住比分布如图4所示。临安区职住比为1,拱墅、江干、富阳三个区职住比为0.99,杭州市总体接近职住平衡状态。 图4 杭州市各个行政区职住比分布图 通过热力图可以显示一个城市在某一时刻通勤人口的聚集情况。通过改进的K-means算法聚类统计空间单元内某一时段的手机用户数量,通过手机用户数量渲染地图颜色制作通勤人口热力图。颜色越深表示通勤人口越集中。 选取2018年3月杭州市(不含富阳、临安)某工作日8:00-9:00的手机定位数据,制作的热力图如图5所示。 图5 杭州市8点早高峰时段热力图 从图中可看出通勤人口主要聚集分布在:① 主城区,主要是西湖景区,武林、湖滨商圈、黄龙商圈等主要商业区域;② 滨江区大部以及萧山区城区部分;③ 余杭区的临平副城;④ 城西的文一路、文二路、文三路及周边区域;这些区段的通勤压力较大,上、下班高峰期容易造成交通拥堵。 将上述采用改进的K-means聚类算法获得的职住比、热力图通勤人口分析分别与杭州市第六次人口普查数据和《杭州交通运行分析报告》(2017年12月发布)进行分析对比,结果基本一致。说明上述改进的K-means算法可用于移动通信大数据下的城市通勤行为特征分析,可为城市交通规划、空间发展规划等众多领域提供服务,应用前景广泛。下一步将通过研究分析通勤距离、时间、成本等指标对杭州市通勤情况进行全面评估,为优化杭州市空间结构布局提供科学依据。2 实 验
2.1 数据准备
2.2 实验环境
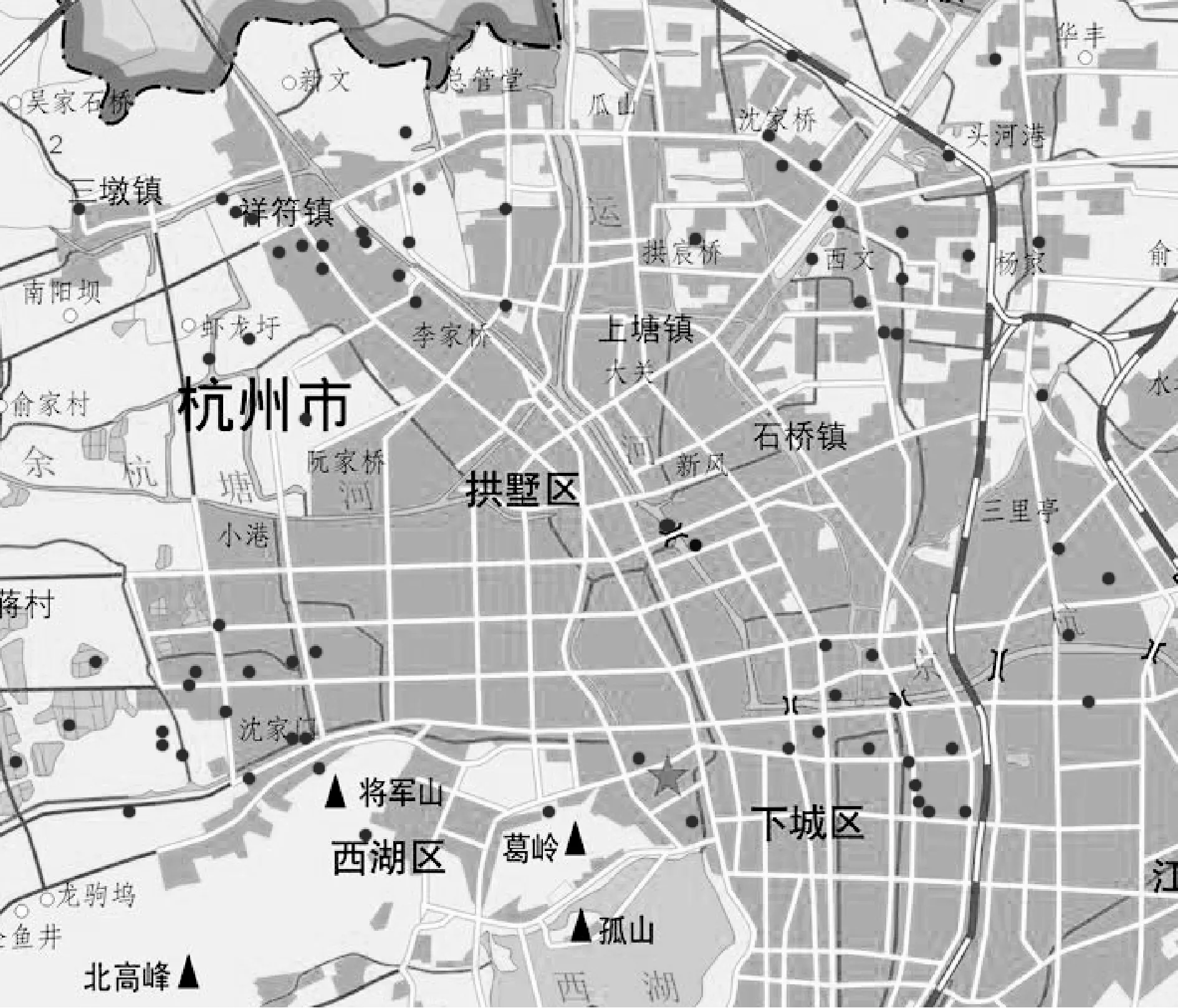
2.3 算法比较
3 算法验证
3.1 位置映射
3.2 职住平衡分析
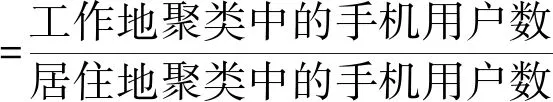
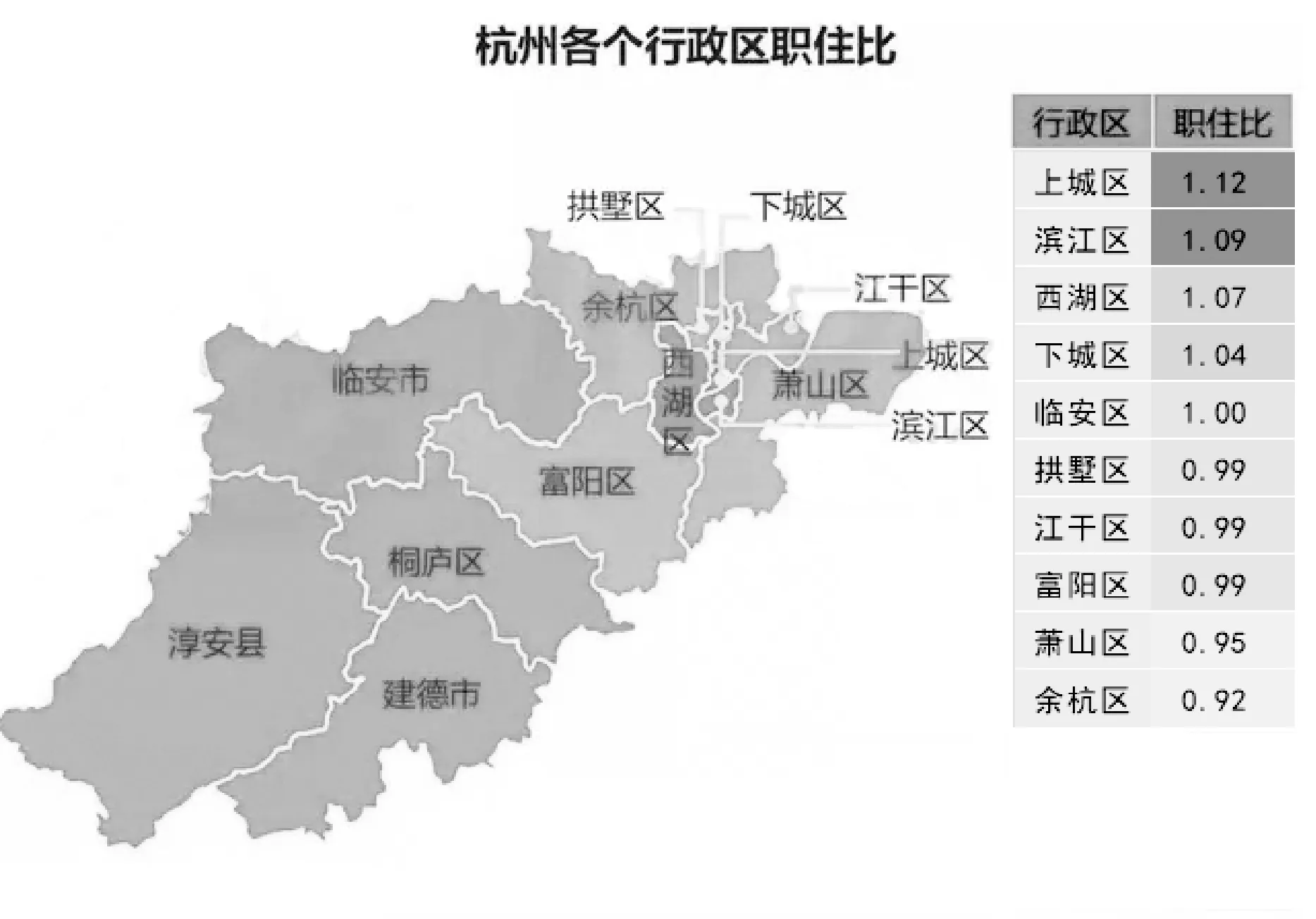
3.3 热力图分析
4 结 语
