基于k-means聚类算法的高校人才评价分析

夏汛

摘要：科研水平是衡量高校发展的一个重要指标，科研对高校的意义和深远价值不言而喻。本文以泸州职业技术学院为例，通过获取泸州职业技术学院的科研论文和科研数据，经过权重设置，归一化处理后，运用k-means聚类算法，分析出整个学院的科研全貌，从而为领导的各项决策提供数据支撑。

关键词：科研;k-means;聚类算法

中图分类号：F239.1 文献标识码：A 文章编号：1007-9416（2019）12-0098-02

1 K-means算法介绍

K-means算法，也被称为K-均值或K-平均算法，是一种广泛使用的聚类算法。K-means算法是基于相似性的无监督的算法，通过比较样本之间的相似性，将较为相似的样本划分到同一类别中。由于K-means算法简单、易于实现的特点， K-means算法得到了广泛的应用。

2 数据准备

通过爬取泸州职业技术学院科研管理系统和知网的科研数据，并将相应的成果赋予一定的权重，取得的科研项目和科研成果分析如图1所示。

3 数据预处理

因为各个指标评价分值不通，为统一标准，使用z-score对数据化做归一化处理。

z分数公式如公式1所示：

（1）

其中μ为总体平均值，X-μ为离均差，σ表示总体标准偏差。z的绝对值表示在标准差范围内的原始分数与总体均值之间的距离。当原始分数低于平均值时，z为负，以上为正。

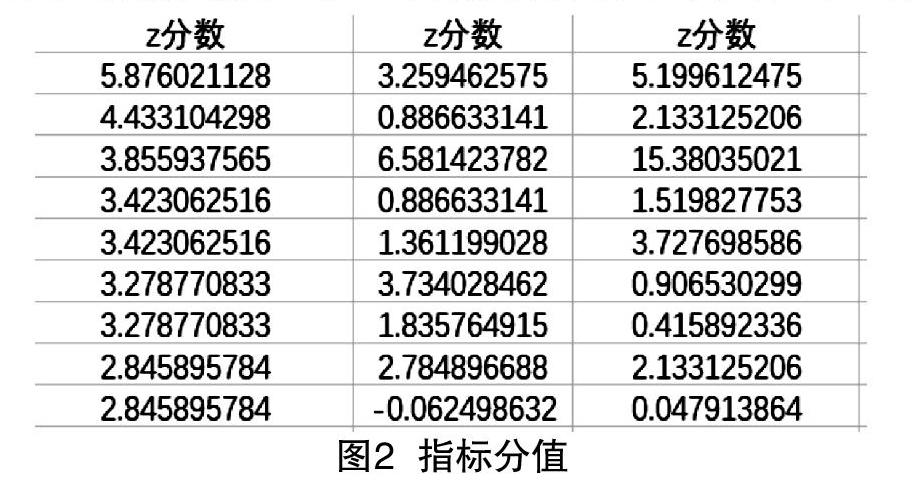
经过归一化处理后，指标分值如图2所示。

4 确定聚类数量

因为该分析中不确定聚类的数量，那么可以通过肘部法则这一技术来估计聚类数量。肘部法则会把不同值的成本函数值画出来。随着值的增大，平均畸变程度会减小;每个类包含的样本数会减少，于是样本离其重心会更近。但是，随着值继续增大，平均畸变程度的改善效果会不断减低。值增大过程中，畸变程度的改善效果下降幅度最大的位置对应的值就是肘部。如图3所示。

可以看出，聚类数量应设定为3。

绘制该图的python代码如下：

df_features = pd.read_csv（r'G：＼计算.csv'， encoding='utf-8'）  # 读入数据

'利用SSE选择k'

SSE = []  # 存放每次结果的误差平方和

for k in range（1， 9）：

estimator = KMeans（n_clusters=k）  # 构造聚类器

estimator.fit（df_features[['R'， 'M']]）

SSE.append（estimator.inertia_）

X = range（1， 9）

plt.xlabel（'k'）

plt.ylabel（'SSE'）

plt.plot（X， SSE， 'o-'）

plt.show（）

5 使用K-means算法计算聚类

继续使用上述数据，进行聚类的绘制。

python的关键代码如下：

##计算欧式距离

def distEuclid（x， y）：

return np.sqrt（np.sum（（x - y） ** 2））

## 初始化簇中心点 一开始随机从样本中选择k个 当做各类簇的中心

def initCentroid（data， k）：

num， dim = data.shape

centpoint = np.zeros（（k， dim））

l = [x for x in range（num）]

np.random.shuffle（l）

for i in range（k）：

index = int（l[i]）

centpoint[i] = data[index]

return centpoint

##进行KMeans分类

def KMeans（data， k）：

##样本个数

num = np.shape（data）[0]

##记录各样本 簇信息 0：属于哪个簇 1：距离该簇中心点距离

cluster = np.zeros（（num， 2））

cluster[：， 0] = -1

##记录是否有样本改变簇分类

change = True

##初始化各簇中心點

cp = initCentroid（data， k）

while change：

change = False

##遍历每一个样本

for i in range（num）：

minDist = 9999.9

minIndex = -1

##计算该样本距离每一个簇中心点的距离 找到距离最近的中心点

for j in range（k）：

dis = distEuclid（cp[j]， data[i]）

if dis < minDist：

minDist = dis

minIndex = j

##如果找到的簇中心点非当前簇 则改变该样本的簇分类

if cluster[i， 0] ！= minIndex：

change = True

cluster[i， ：] = minIndex， minDist

## 根據样本重新分类  计算新的簇中心点

for j in range（k）：

pointincluster = data[[x for x in range（num）

if cluster[x， 0] == j]]

cp[j] = np.mean（pointincluster， axis=0）

6 数据结论

通过最终得到的聚类图，结论如下：

（1）教师可以分为A、B、C三大类;（2）A类教师在科研项目、学术论文方面均明显高于其它教师，学院的科研项目、核心期刊主要由这部分教师完成，可视为优秀科研型教师;（3）B类教师水平较为中庸，在科研项目和学术论文方面均有所产出，但在核心期刊方面产出较少，可视为科研项目型教师;（4）C类教师产出较低，在科研项目和学术论文方面只有极低产出，或者只有一方面有产出，该部分教师基本未参与科研;（5）注意到聚类图里的几个离散点，数量较少，仅有几名，可视为科研领军型人物，在科研项目和学术论文方面均遥遥领先。

参考文献

[1] 张海林，李琳，夏传良.改进K-means算法的馈线线损计算[J].软件导刊，2019（11）：1-5.

[2] 程士卿，郝问裕，李晨，等.低秩张量分解的多视角谱聚类算法[J].西安交通大学学报，2019（03）：1-7.

The Analysis of  Talent Evaluation in Colleges and Universities Based on K-means Clustering Algorithm

——Taking Luzhou Vocational and Technical College as an Example

XIA Xun

（Luzhou Vocational & Technical College，Luzhou  Sichuan  646005）

Abstract：the level of scientific research is an important indicator to measure the development of colleges and universities. The significance and far-reaching value of scientific research to colleges and universities are self-evident. This paper takes Luzhou vocational and Technical College as an example， through obtaining the scientific research papers and data of Luzhou vocational and technical college， after weight setting and normalization processing， using k-means clustering algorithm， analyzes the scientific research panorama of the whole college， so as to provide data support for leaders' decisions.

Key words：scientific research;k-means;clustering algorithm