Development and Research Status of Turbulence Model

DENG Rui,GAO Zi-yu,LI Yu-long,JIANG Da-peng,MA Yong

(School of Marine Engineering and Technology,Sun Yat-Sen University,Guangzhou 510275,China)

Abstract:Since the DNS(Direct Numerical Simulation)method is hard to achieve because of the hardware condition nowadays,many turbulence models are widely used in the research of the computational fluid mechanics.The development of the turbulence models started from RANS and URANS,advanced in LES and DES,and modified in many hybrid methods.Though nearly all of the models had successful cases in application,the shortcomings of them are unavoidable.This paper takes primary comparison and discussion of RANS/URANS,LES/DES and Hybrid RANS-LES,the features of each are discussed basing on the development and the overcoming of the former’s shortcoming,some application of each turbulence model are also included.

Key words:turbulence model;RANS(Reynolds-averaged Navier-Stokes);LES(Large-Eddy Simulation);DES(Direct Numerical Simulation);hybrid method

0 Introduction

This paper focuses on the different turbulence models used in the engineering application and academic research.The first part is a brief discussion on RANS(Reynolds-averaged Navier-Stokes)and URANS(Unsteady Reynolds-averaged Navier-Stokes).Though they are developed for decades and mature,even being widely applied in engineering,the history and the introduction are ignored,only the features are discussed.Because the details of the flow field are much more attractive,the second part is to disscuss LES(Large-Eddy Simulation)and DES(Detached-Eddy Simulation),which are capable of capturing the flow field details.Where LES seems to be a realizable way for DNS(Direct Numerical Simulation)and DES is supposed to be an alternative approach for LES.For this part,some brief information about DES and the method derived for the classic DES is introduced,as well as the application and improvement of LES and DES.In the last part,considering the inherited defects of DES,which are not easy to overcome,some Hybrid RANS-LES models,which are advanced,are introduced.The Hybrid RANS-LES model is relative new and blooming,so some necessary information is needed in statement,analysis,comparison,discussion,as well as the application.The last two parts are highlighted.

1 RANS models and URANS

Reynolds-averaged Navier-Stokes(RANS)models provide results for mean quantities with engineering accuracy at moderate cost for a wide range of flows,and the field of classical RANS turbulence modelling is active.At a biennial international symposium,about 25 papers presented new models or new versions of models[1],isolated groups are refining integral boundarylayer solvers,to allow more three-dimensionality and more separation.The same seems to apply to algebraic models.Eddy-viscosity transport models,being the simplest models that can be applied with a general grid structure,are now used extensively.The step back from two equations to a single equation has not crippled the approach[2-5],while tangibly reducing the true cost of solutions(partly by allowing a coarser grid spacing at the wall).Conversely,models with up to four equations are in contention[6-7].

Complete configurations often have laminar regions in their boundary layers;it is very helpful if a turbulence model can be ‘dormant’ in such regions,meaning that its transport equations accept solutions with vanishing Reynolds stresses.Similarly,regions of irrotational and non-turbulent fluid,which are large in external aerodynamics,do not physically influence the turbulent regions such as boundary layers.At the same time,the model should allow the contamination of a laminar shear layer by contact with a turbulent shear layer.This all depends on the behaviour of the model at the turbulent/non-turbulent interface.In some models the stress level in the turbulent layer depends demonstrably on either the freestream values of the turbulence variables or,even worse,on the grid spacing at the interface.Few people have devoted attention to this question[4,8-9],and model descriptions sometimes make no mention of recommended freestream values.However,it happens that the k-ε,SST and S-A models,which all three are insensitive to freestream values,and so that freestream sensitivity should be given high priority.

The URANS relys on traditional RANS models but is deliberately unsteady,even with steady boundary conditions.Fig.1 shows simulation of flow past circular cylinder by various approaches.

Fig.1 The difference in description for the flow past a circular cylinder(Shur et al,1996;Travin et al,2000)

For instance,vortex shedding is allowed past a bluff body[10-13].Durbin correctly noted that the Reynolds stresses created by the time averaging of the URANS solution overwhelm those carried by the model itself,in the separated region,and therefore remove much‘responsibility’from that model[6].It is simple to describe how to conduct a URANS,but the physical implications give pause.For simplicity,consider vortex shedding by a bluff body and assume that URANS gives a periodic solution,which is typical[6,12,14-15].If a flow field is assumed to be periodic in time and smoother than the true turbulent field but representative in some sense,its inviscid dynamics mirror the large-scale dynamics of the true flow.However this ignores the amplitude modulations,which are strong for bluff bodies and have overwhelmed experimental and simulation evidence[14-15].The phase-averaging creates Reynolds stresses of two kinds,and in URANS both are left to the turbulence model.The expected kind,due to incoherent smallscale motions,appears amenable to common modelling.The trouble some kind is that due to modulations in the shedding.The difference between fields at the same phase in different cycles is just as coherent as the difference between these fields and the long-term time average.It is just as difficult to model with the simple common approximations.Fortunately,it is smaller.Nevertheless,it is not rigorous to state that,with URANS,the turbulence model is responsible only for ‘incoherent’ motions.Furthermore,the interpretation that only random and presumably weak turbulence is appropriate for modelling is inconsistent with the simple fact that the models are usually adjusted to reproduce the spreading rate of mixing layers in RANS mode.Yet the mixing layer is notorious for its coherent vortices,which span its whole width and pair in obvious discrete events.Another slant is to observe that URANS implies a separation of time scales,between that of the visible shedding and that of the putative residual turbulence,which is not indicated in measurements.

2 LES and DES

Away from boundaries and without chemistry,Large-Eddy Simulation(LES)appears well understood,and there is little to gain by refining the SGS models[16].Fig.2 shows the visualization of high-intensity vorticity regions in LES of isotropic forced turbulence using different SGS models at ReT≈94.

Fig.2 Visualization of high-intensity vorticity regions in LES of isotropic forced turbulence using different SGS models at ReT≈94(Fureby et al,1997)

Some proposals appear to add mathematical rigor[17-18],but amount to accounting changes.Others use sensible approximations,but fail to show a clear advantage over the same-cost LES with a simplistic model,which would have a slightly finer grid.Issues such as non-commutativity between the filtering and differencing operators are valid,but their leverage is probably small compared with SGS modelling errors.It is even possible to run an LES without any SGS model,simply using an upwind or monotone numerical scheme to offset the energy cascade and maintain the smoothness of the solution but such an exercise is not greeted by those who built careers on SGS modelling[19].A much more serious concern is that SGS-free LES cannot deal with the wall region of the boundary layer(except by approaching DNS).In the wall regions,it is fair to describe most of the current LES work as Quasi-Direct Numerical Simulation(QDNS)[20].

The SGS stresses are of the same order of magnitude as the viscous stresses,since typical eddy-viscosity levels are very close to the molecular viscosity,but an accurate and reliable‘true’ or ‘full’ LES,meaning that the Reynolds number based on the grid spacing is unlimited,appears to be a difficult goal.Presumably the community switched to QDNS,although the pioneering work[21-22]was full LES,in order to reduce empiricism in the near-wall treatment.In full LES,the grid spacing in all directions would scale with the boundary-layer thickness,for a given level of accuracy.Fot this reason,SGS modelling is expected to be improved,and it is unavoidable that empiricism will be added,or at least,such a treatment would have to imply values for the constants in the logarithmic law.

At a recent LES workshop,a variety of QDNS and full-LES methods were applied to fairly simple geometries with sharp corners[23].In spite of these helpful features,the conclusions were particularly mixed,and did not make LES or even QDNS appear very mature.The flow past a circular cylinder,even at Reynolds numbers of a few thousand,has also led to quite different levels of agreement with experiment,for instance the results of both SGS-model improvements and grid refinement[24]are not satisfied.SGS models also remain a lack of maturity and/or in different progress.A typical example even with the best wall-region treatment,is very far from affordable in aerodynamic calculations,and will be for decades[20],which is due to the large regions of very thin boundary layers,and led us to propose Detached-Eddy Simulation(DES),a further step in the hybridization of LES[20].The idea of DES is to entrust the whole boundary layer to a RANS model and only separated regions to LES,which leads to a manageable computing cost even at high Reynolds numbers[25-26].Fig.3 shows the DES grids over NACA 0012 airfoil.

An attractive feature of DES is that it is simply formulated,being tested,and only requires a quick alteration of the S-A one equation model.DES results for an airfoil at high angles of attack have been presented[25].Fig.4 shows th average forces over a wide range of angle of at-tack α.

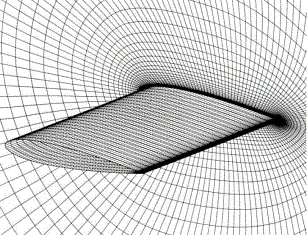
Fig.3 DES grids over NACA 0012 airfoil

At high angle of attack the agreement with experiment is surprisingly good,but not better than in the best examples of DNS and LES for bluff-body flows[27-28]at lower Reynolds numbers.DES will require definite skills from the user in directing the grid resolution;however,RANS also benefits from careful grid generation.A few patient RANS users are refining grids manually after exploring preliminary solutions[29],but many solutions are under-resolved in the separated regions.In the work of Travin[15],the results of steady RANS are too low,and the ones of URANS are much too high,but the DES drag is in much better agreement with experiment.Turbulent boundary layers also can be obtained with an appropriate nonzero inflow value[15];the key is to selectively set the inflow and the initial conditions.Some similarities between DES and past treatments of the wall region in LES[21-22,30]may suggest from a narrow focus that DES is a simple hybrid of RANS and LES.The similarities are not in the details that are vastly different between methods but merely in the position that the near-wall flow field,averaged over a grid cell,behaves closely enough to a full Reynolds-averaged flow that the law of the wall and/or RANS modelling technology are good approximations.Since the accuracy is acceptable in boundary layers,DES is possible now with reasonable ambitions of accuracy,and tested in a channel,with LES grids[26].The approach would switch to LES upstream of any intense pressure gradients,which tentatively makes another step up in accuracy.The difficulties are the ‘artificial intelligence’ of identifying where the switch should be located;the generation of quality turbulent eddies for the RANS region to dispatch into the LES region(the regions might have to overlap).The‘eddy seeding’problem appears less severe with DES,because a separated shear layer is exposed to vigorous new instabilities[31]and these new instabilities overwhelm the boundary layer turbulence.If the instabilities do not,for instance in a separation bubble,DES cannot be expected to provide much improvement over RANS.

Recently,noticeable progress has been reached in building hybrid RANS-LES models for both high Reynolds number massively separated flows and more general cases that also include attached and mildly separated regions.For the former,probably the most popular approaches are detached-eddy simulation or DES(DES97)[32],and its recent modification,delayed DES(DDES)[33].Fig.5(a)shows grids of DDES over back-ward facing step,and Fig.5(b)shows the comparison between DES97 and DDES,showing that LES content is essentially as fine with either approach,both in the free shear layer and in the reattaching wall layer.

Fig.4 Lift and drag coefficients(—Exp.Re=106;---Exp.Re=105;○DES Re=105;□ DES Re=3×106;△ URANS Re=105(Shur et al,1999)

Fig.5 Grids of DDES over back-ward facing step and comparison

A general feature of these two approaches is that the whole or at least a major part of the attached boundary layer is treated by RANS,while LES is applied only in the separated flow regions.In contrast,in a second group of RANS-LES hybrids,which offers wall-modelling in LES(WMLES)of high Reynolds number flows,RANS is used only in a much thinner nearwall region,in which the wall distance is much smaller than the boundary-layer thickness[34].Along with this,similarly to DES97 and DDES,in the attached flow regions these models use‘RANS grids’,i.e.,they employ highly anisotropic grids with very large(‘unlimited’ in wall units)grid spacing in the directions parallel and adjacent to the wall.Unfortunately,most WMLES approaches in the literature are zonal,and include some ‘channel-friendly’ steps,i.e.,elements that are easily implemented in channel flow but whose applicability in more complex flows is debatable.Other than that,some proposed solutions use substantial outside information such as fields from wall resolved LES or DNS runs[35]or synthetic turbulence[36]at the RANS-LES interface,or require averages in the wall-parallel directions to define intermediate quantities[37]or to avoid negative eddy viscosity and similar difficulties.Although rather successful in some cases,all these and other similar models are not completely formulated for cases where a complex geometry is involved.The limited numerical scales approach of Batten et al[38],which shares the simplicity and non-zonal nature of DES97,is capable of natural DES,and was used for WMLES in a channel[39](Fig.6).

It did better on a very coarse grid,with weak resolved stress,than in a more conventional situation with LES dominance of the outer layer.The WMLES approach of Abe[40]has many similarities with the present one both in terms of purpose and level of complexity.Its capability in natural DES mode is not mentioned in that paper,but the RANS model appears to have a standard k-ε behaviour and therefore should cover the entire boundary layer,provided the grid is not‘ambiguous’ as defined by Spalart et al[33].The work of Schiestel and Dejoan[41]is similar in the sense that they also aim at the full range from RANS to LES,but again do not avoid grid densities,and their derivation has a theoretical flavour.The wall-normal stretching is also very rapid in places.Note that the DES formalism can also be used for WMLES,and this does not imply any additional complexity and/or impractical.The first attempt to do this in the developed channel flow[42]turned out generally successful in the sense that the approach,enabled LES predictions at unlimited values of grid spacing parallel to the wall in wall units.The simulations produced two logarithmic layers：the ‘inner’log-layer,which arises because the RANS model is constructed to provide it and the ‘outer’log-layer,which arises because LES is functioning well once all local grid-sizes are much smaller than the distance to the wall,but these two log-layers turn out mismatched because of the different intercepts,resulting in an under-prediction of the skin-friction by up to 15%-20%,an error that is far too large to meet the demands of the aerospace industry.This flaw in DES is completely inherited by DDES;neither method has so far been adjusted to deal with the mismatch because WMLES was not their primary application.Thus,there is a strong motivation to find a remedy of log-layer mismatch(LLM)within a non-zonal,DES-like approach.

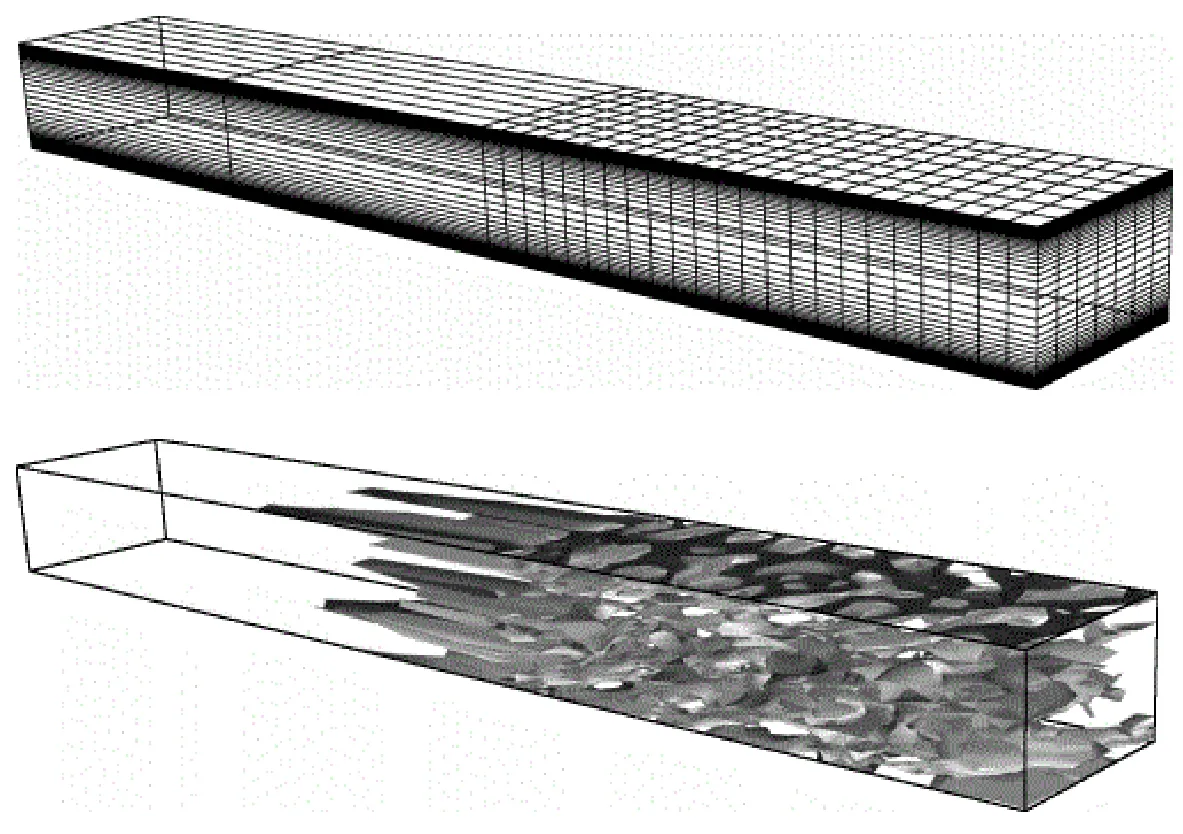
Fig.6 Channel-flow grid showing streamwise clustering(up)and instantaneous streamwise vorticity isosurfaces shaded with the streamwise velocity component(bottom)(Batten et al,2004)

3 Hybrid of RANS and LES

DES97 adjusted the scale in the classic S-A(Spalart-Allmaras)[4]RANS,and being widely used in many successful cases[25,43-46].But,the severe insufficient in the transition from RANS to LES still exists,even DDES improved this problem mildly,the improvement increases the sensitivity of the results on the filed[47],especially when the interface is in the boundary layer[48].

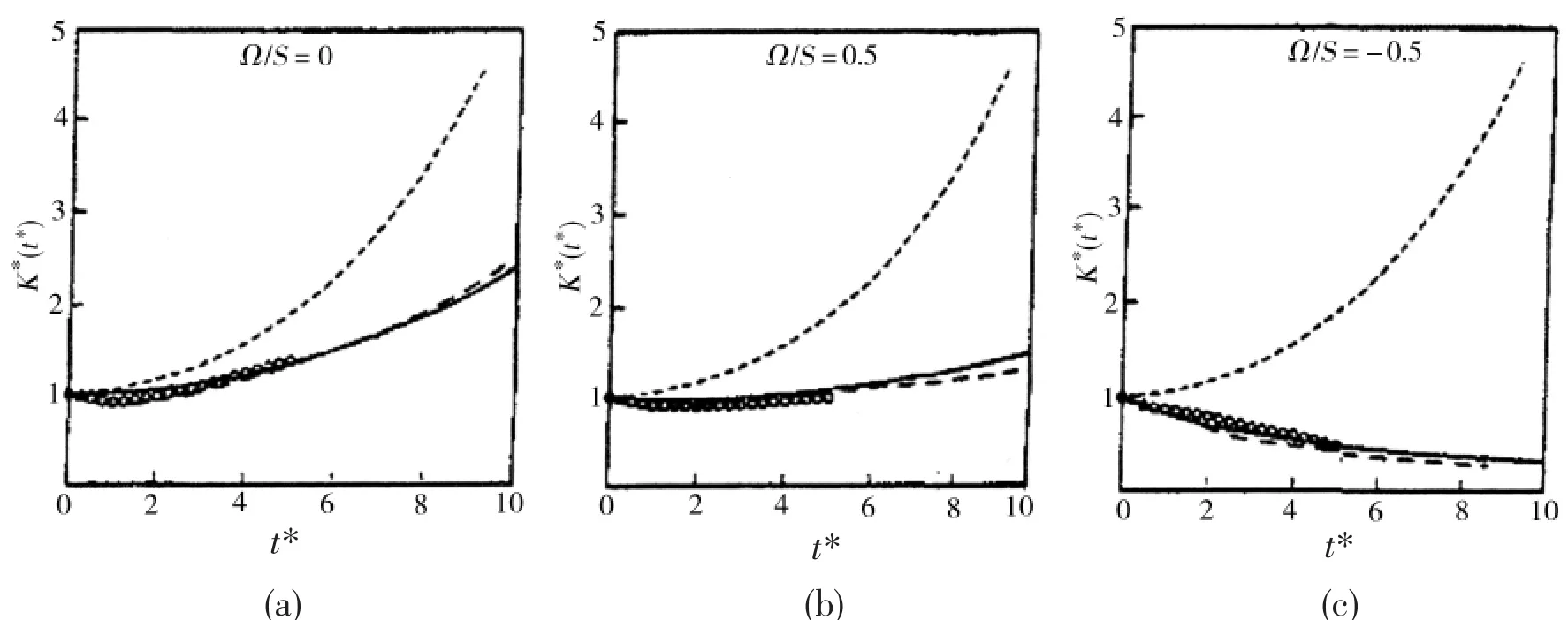
Fig.7 Time evolution of the turbulent kinetic energy in rotating homogeneous shear flow：Comparison of the model predictions with the large-eddy simulations.Ω means angular velocity;S means constant shear rate

In order to overcome the shortcoming of the DES,a hybrid method which is on the basis of RANS is developed and has a complete potenital in the engineering for the complex problem[47].The pure RANS calculation,although applied as unsteady RANS,failed to predict the unsteady characteristics of the separated flow.In contrast,the DES approach yielded reasonably the shedding phenomenon and some integral parameters.Thus,the new idea is to use LES in small localized subdomains where an accurate description of the flow is wanted, while computing the rest of the configuration with a Reynolds averaged numerical simulation(RANS)approach[49].Fig.7 shows the comparison of the model predictions with the large-eddy simulations.

The problem in this method is to define adequate interface conditions between RANS and LES subdomains,which is a fully general multi-domain problem,and is a generalization of the LES multi-resolution/multi-domain approach[50].Theoretical analysis reveals that the solution is discontinuous at the RANS/LES interface,and that even the dimension of the solution can vary.The proposed treatment is based on the definition of an interface variable,which is extrapolated from the LES subdomain or extracted from an auxiliary computation,depending on the type of interface[51].Fig.8 shows a partial view of the mesh ratio across the interface.

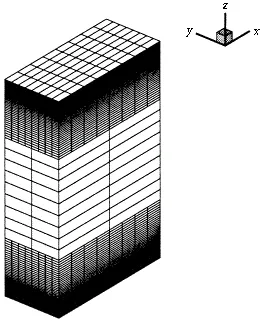
Fig.8 View of a piece of mesh in multidomain case

The method overcomed the deficiencies of DES,in which the free shear layer was not well reproduced because the Kelvin-Helmholtz instability is not reproduced adequately and the model is applied as a subgrid scale model[52].When a hybrid LES-RANS model in which unsteady RANS is used in the near-wall region,and the turbulence is modelled with a k-ω model,while LES is used in the core region and the SGS turbulence is modelled with a one-e-quation SGS model for the channel flow and hill flow[53],one major problem is that the flow provided by the unsteady RANS to the LES region across the matching plane does not have proper spectral properties.But an approach that resolved turbulent fluctuations u′,v′,ω′are superimposed on the RANS velocities,¯,at the matching plane has been tested for channel flow and the flow in a asymmetric diffuser,and the results are very promising[54].Also,a possible path for developing a large eddy simulation(LES)applicable to high Reynolds-number turbulent flows is presented by Abe[55],in which an advanced nonlinear eddy-viscosity model is introduced to resolve the near-wall stress anisotropy more correctly.

Benarafa tried to give prominence to the drawbacks of LES+SWM results with very coarse resolution grids[56]but strong discrepancies appear between the mean velocity profile and the log law and the wall shear stress was badly estimated.The other problem is the streamwise velocity fluctuation created an abnormally large buffer layer.Then,an attempt was to use a more sophisticated wall model(TBLE wall model)which could evaluate better the wall shear stress and improve the previous results.In contrast to Benarafa’s work,the cost of the method is investigated by combining a LES scheme with different near-wall RANS approximations by reference to simulations for plane channel flow and two separated flows at moderate and high Reynolds numbers[57].The research shows that the hybrid approach is more expensive,but allows the interface to be placed further away from the wall and to provide a numerically consistent framework.

On the issue that the generation from a smooth RANS field of turbulent eddies capable of supporting the Reynolds stresses in the LES region may affect the accuracy of the results of hybrid methods is,Keating[58]performed hybrid RANS/LES of turbulent boundary-layer flows in zero,favorable and adverse pressure-gradients.Fig.9 shows a sketch of the computational configurations.

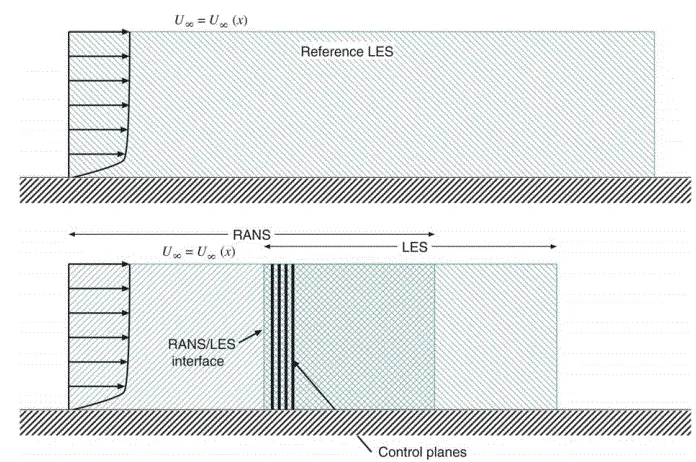
Fig.9 Sketch of the numerical configuration,U∞refers to average velocity(Keating et al,2006)

Synthetic turbulence and controlled forcing are used to generate turbulent structures in the LES region,and some distance is required before the proper phase.At last,the hybrid sim-ulations were in good agreement with full domain LES.Later,an improvement by Davidson[59]consists of adding instantaneous turbulent fluctuations(forcing conditions)at the matching plane between the LES and URANS regions in order to trigger the equations to resolve turbulence is presented on this method.Another new hybrid model,IDDES,plausibly combining DDES and WMLES capabilities is proposed by Shur[60],which is shown to resolve the issue of mismatch between the modelled log layer and the resolved log layer,and the method has been typical of either DES or DDES use for WMLES.Fig.10 shows that IDDES does capture the major known features of the turbulence in the channel reasonably well.

Fig.10 The advantages of IDDES are clearly seen in a direct comparison of the flow visualizations from the simulations with the use of this model and MSST-based DDES.H means thickness of boundary layer(MikhailL et al,2008)

Two versions of IDDES,based on the SA and MSST background RANS models,are simple in implementation,and already independent applications of an earlier version of IDDES[61]by Piomelli et al[62]and by Mockett et al[63].A way to justify the method of additional filtering at the RANS/LES interface is proposed by Hamba[64].A two-dimensional filtering with the filter width ranging from the grid size to the RANS length scale is introduced as a hybrid filter[65].

Improvement of the additional filtering at the RANS/LES interface is then attractive.A coupling methodology between an upstream Reynolds Averaged Navier-Stokes(RANS)simulation and a Large Eddy Simulation(LES)further downstream was presented by Jarrin[66].The focus is on the RANS to LES interface inside an attached turbulent boundary layer,where an unsteady LES content has to be explicitly generated from a steady RANS solution.The partially integrated transport modelling(PITM)method can be viewed as a continuous approach for hybrid RANS/LES modelling allowing seamless coupling between the RANS and the LES regions.The subgrid turbulence quantities are thus calculated from spectral equations depending on the varying spectral cutoff location[67-68].The PITM method can be applied to almost all statistical models to derive its hybrid LES counterpart.The PITM version based on the trans-port equations for the turbulent Reynolds stresses together with the dissipation transport rate equation is now developed in a general formulation[69]based on a new accurate energy spectrum function valid in both large and small eddy ranges.Some modify is performed by Martín Sánchez-Rocha[70]on the interface filter,which is constructed by linearly combining the Reynolds-average(RANS)and large-eddy simulation(LES)operators with a continuous blending function.The derived hybrid equations include additional terms that represent the interactions between RANS and LES formulations.Results show that when the additional terms are included,the calculations are not very sensitive to the blending function implemented in the hybrid filter.In the contrary,when these terms are neglected and a step function is implemented in the hybrid filter,nonphysical discontinuities are predicted in the flow statistics.Some succesful cases are offered[71-73].

The transion of RANS to LES is also an issue in the recent years.Laraufie et al[74]provided an efficient and flexible method for the initialization of a zonal RANS/LES type calculation when the resolution of the near wall region was treated in RANS mode.A self-adaptative dynamic forcing approach based on innovative considerations,comes from its local nature,enabling to treat geometrically complex applications.It dramatically increases the efficiency of the inflow generation and reduces the transition distance up to 76%compared to the SEM inflow by itself,when a RANS/LES type resolution is employed.Shur[75]introduced a procedure which rests on a double-coverage of a region of the boundary layer and enables an essentially immediate switch at a chosen location from RANS,without resolved eddies,to LES,with resolved eddies carrying the Reynolds stresses in the outer part of the boundary layer.Based on this idea,Heng Xiao[76]proposed a consistent turbulence-modeling framework for hybrid LES/RANS modeling in which the filtered and Reynolds averaged Navier-Stokes(RANS)equations are solved simultaneously in the whole domain on their respective meshes.Different approaches were presented and their capability to accurately generate the needed aerodynamic values was investigated by Laraufie[77],on the transition from a RANS to a LES or WMLES resolution in the stream-wise direction,when near wall turbulence is involved.Then,the important intrinsic features of the synthetic eddy method are pointed out.

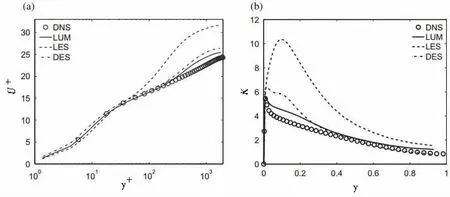
Fig.11 Comparison of the mean streamwise velocity and total turbulent kinetic energy obtained with LES,DES,the LUM and DNS at Re=2000(Harish Gopalan et al,2013)

Some comparison and evaluation of the hybrid method are then performed by the researchers.The properties of an optimal hybrid RANS-LES model are formulated by taking reference to fundamental properties of fluid flow equations by Gopalan[78],in order to find a hybrid RANS-LES method represents the optimal approach.Fig.11 shows the comparison of results obtained with LES,DES,LUM dan DNS methods.

Predictive capabilities of hybrid RANS/LES models were compared by Bhushan[79]for single-phase flow over a surface combatant at Re=5.3×106and an appended DARPA Suboff model at Re=1.2×107.Five Large Eddy Simulation(LES)and hybrid RANS-NLES(Reynolds-Averaged Navier-Stokes-Numerical-LES)methods are used to simulate flow through a labyrinth seal geometry and are contrasted with RANS solutions[80].

A further improvement is under performed,such as a new method using a general-purpose finite-volume flow solver was highly generalized by Walters[81],allowing coupling of any selected RANS model with any selected LES model and containing no explicit grid dependence in its formulation.A synthetic turbulence generation(STG)method for subsonic and supersonic flows at low and moderate Reynolds numbers to provide inflow distributions of zonal Reynolds-averaged Navier-Stokes(RANS)-large-eddy simulation(LES)methods is presented,and the STG approach reduces the RANS-to-LES transition length to less than four boundary-layer thicknesses[82].A trategy which blends a variational multiscale large eddy simulation(VMS-LES)model and a RANS model in a hybrid approach was investigated by Moussaed[83].A smooth blending function,which is based on the value of a blending parameter,is used for switching from VMS-LES to RANS.Different definitions of the blending parameter are investigated.

It seems that the investigation and the application of hybrid RANS-LES method bloom rapidly after the invention of it,modify and new strategies drive the approach under developing.

4 Summary

The present paper takes primary comparison and discussion of RANS/URANS,LES/DES and Hybrid RANS-LES,the features of each are discussed basing on the development and the overcoming of the former’s shortcoming.However,DES and Hybrid RANS-LES are the core of the discusstion,some novel ideas and evaluation are included.And,some superficial points of view may be suggested：(1)Considered to RANS,most of the models have the significant advantage that the quality of predictions is relatively independent of the RANS model applied.(2)Considered to LES,the significant advantage of the DES model is a cost reduction of high-Reynolds number simulations,but the shortcoming of DES still exsits.(3)Considered to the usually applied hybrid RANS-LES models,it is shown that they provide significantly improved predictions in mean flow and high Reynolds number condition[84],while resolving small-scale turbulent structures,some of them even effective for coarse grids.Results also highlight the importance of the wall function formulation for accurately resolving mean skin friction coefficient,especially over smooth regions[79].

Acknowledgements

This work was partically supported by the National Natural Science Foundation of China(Grant No.51679053;51779062);the Foundation of Pre-research on Military Equipment of the Chinese Peoples Liberation Army(Grant No.6140241010116CB01005);the Aeronautical Science Foundation of China(No.201723P6001).We would like to thank for the support provided by the Fluid Mechanics Group leaded by Duan Wenyang of Harbin Engineering University.