提高回归模型拟合优度的策略(Ⅳ)——优化计分变换与其他变量变换

胡良平

(1.军事医学科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

1 回归建模前的变量变换[1]

1.1 对多值名义自变量进行“优化计分变换(Opscore)”或“单调变换(Monotone)”

1.1.1优化计分变换

优化计分变换就是采用Fisher[2]提出的给多值名义变量或多值有序变量各水平赋值的方法。Opscore(x)代表对变量x进行优化计分变换，它可以被用于“多值名义变量”或“多值有序变量”。

1.1.2 单调变换

单调变换就是采用Kruskal提出的给多值有序变量各水平赋值的方法(被称为次要最小平方单调变换)。Monotone(x)代表对变量x进行单调变换，它只能被用于“多值有序变量”。

1.1.3 “优化计分变换”与“单调变换”的具体做法

两者具体的变换方法是相同的，每一个不同的非缺失值形成一个不同的类，例如：“1,1,1,2,2,3”形成三类，即3个“1”算作一类、两个“2”算作一类、一个“3”算作一类。具体赋值方法参见下面的实例：

设变量x的具体取值为( . . .A .A .B 1 1 1 2 2 3 3 3 4)' ；设变量y的具体取值为( 5 6 2 4 2 1 2 3 4 6 4 5 6 7)' 。

【说明】以上“x”与“y”都有14个取值，用“向量”形式表示，即这两个向量都有14个分量。其中，变量x的前两个分量都是缺失值“.”；第3和第4个分量都是“.A”；第5个分量是“.B”；第6～14个分量都是数字。而变量y的全部14个分量都是数字。

于是，以“y”为“因变量”，对“变量x”进行“优化计分变换”和“单调变换”。用关键词表示为：Opscore(x)和Monotone(x)。它们只有8个分量，即：

Opscore(x)=( 5 6 3 2 2 5 5 7)'

Monotone(x)=( 5 6 3 2 2 5 5 7)'

【说明】在“x”的向量中，最前面的两个缺失值各形成一类，即有两类；“.A”出现了两次，形成一类；“.B”形成一类 ；三个“1”形成一类；两个“2”形成一类；三个“3”形成一类；一个“4”形成一类，故总共形成8类。

在同一类中，求出“对应于因变量y全部数值的算术平均值”，赋值给变换后的“变量x”，作为其“优化计分变换”或“单调变换”的结果，例如：两个“.A”对应着变量y的两个数值为2和4，其算术平均值为3；同理，三个“1”对应着变量y的三个数值为“1、2、3”，其算术平均值为2；两个“2”对应着变量y的两个数值为“4与6”，其算术平均值为5；三个“3”对应着变量y的三个数值为“4、5、6”，其算术平均值为5；一个“4”对应着变量y的一个数值为“7”，其算术平均值为7。

1.2 可对定量变量进行的变量变换的种类

1.2.1 变量扩展

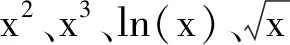
1.2.2 非优化变换

非优化变换就是用一个变换后的“新变量”取代“原变量”。这个“新变量”在后续的迭代算法中不再被重新变换了(对具有缺失值估计所做的可能的线性变换除外)。常用的“非优化变换”有如下几种。

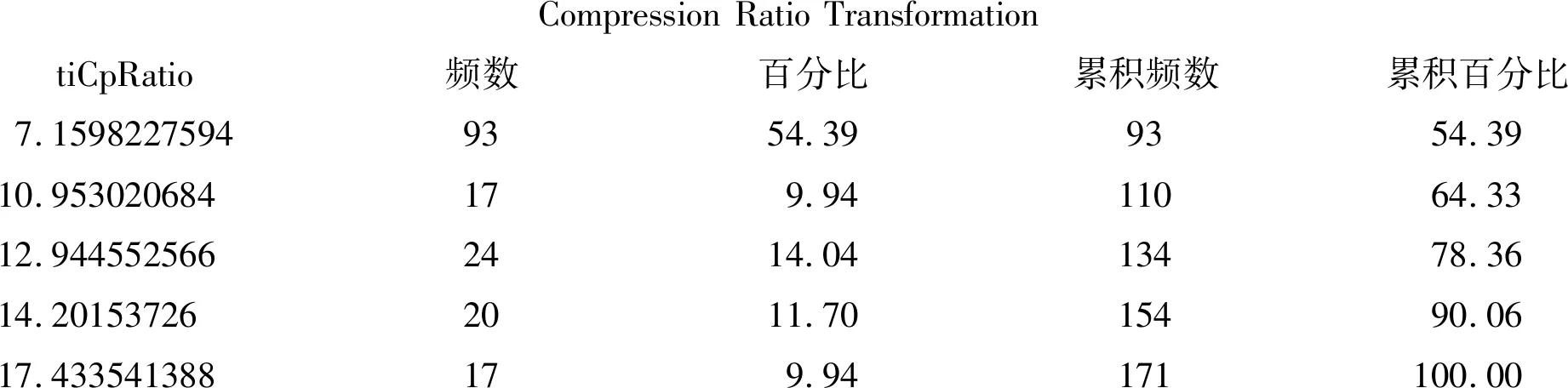
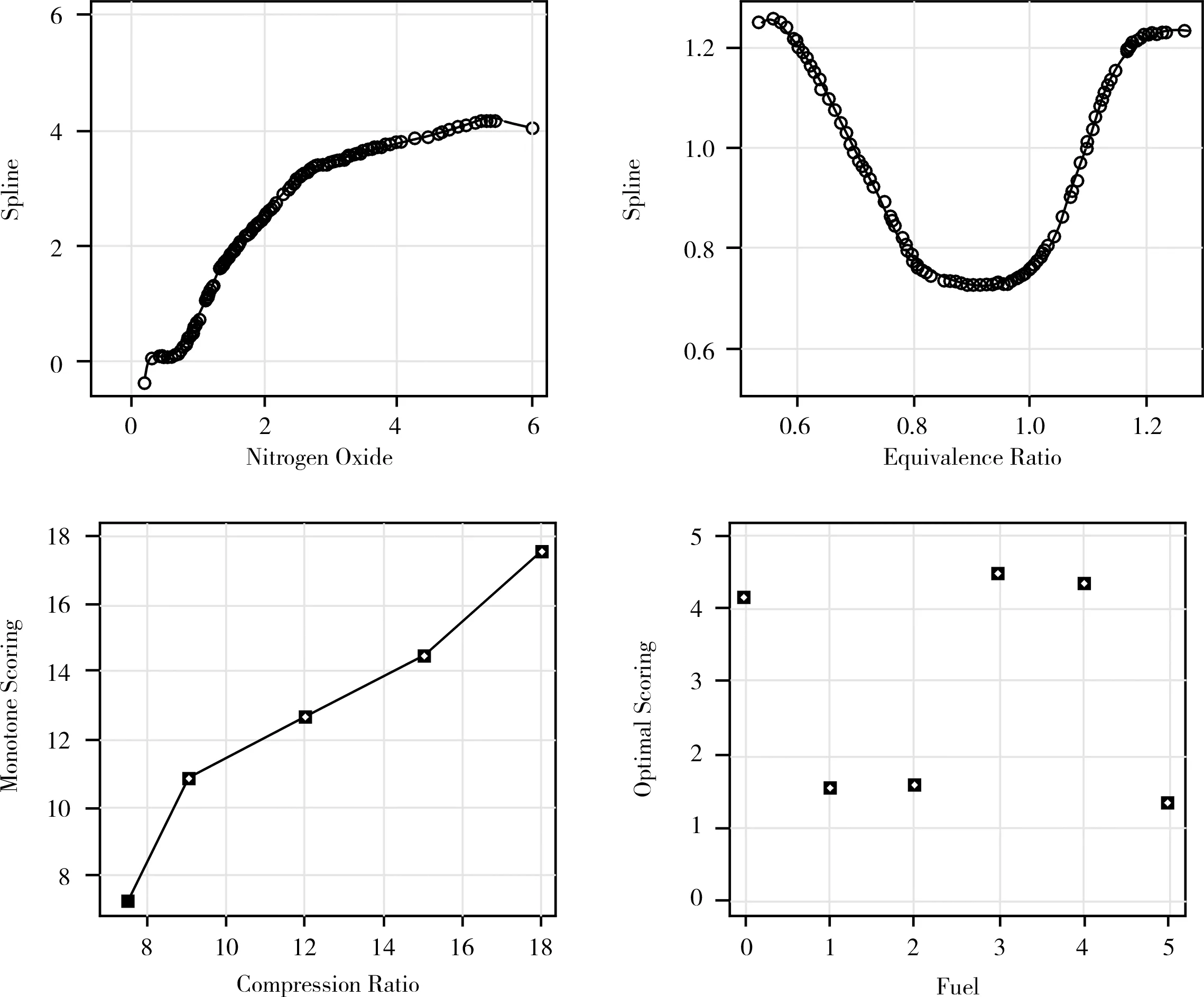
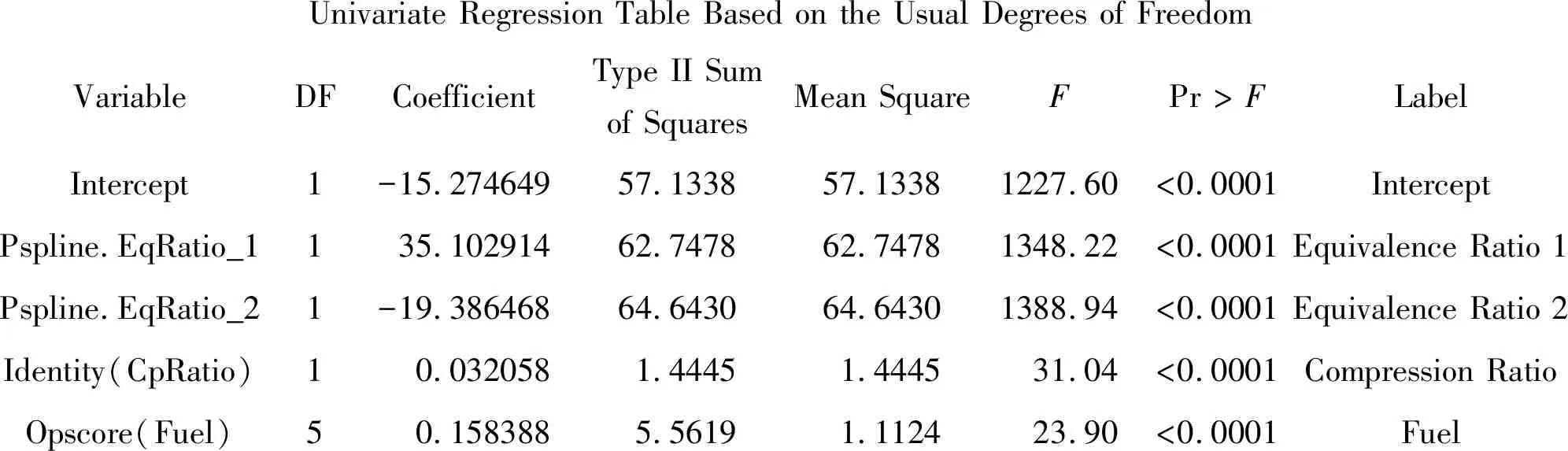
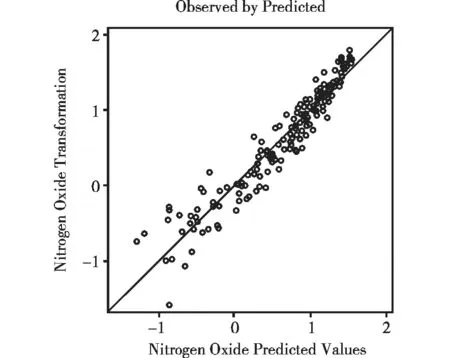
ARSIN(x)：此处的“x”为“百分率”数据，通常其取值区间为“0

EXP(x)：指数变换，通常为“ex”变换；若希望底数为任意的正实数a，即做“ax”变换，在使用SAS的“TRANSREG过程”中，需要另外再使用“Parameter=”来指定，即在“=”后写出“a”的具体数值。

LOG(x)：对数变换，通常取以“e”为底数的对数(e=2.718281828)，即取自然对数变换；若希望底数为任意的正实数a，即做“logax”变换，在使用SAS的“TRANSREG过程”中，需要另外再使用“Parameter=”来指定，即在“=”后写出“a”的具体数值。

LOGIT(x)：logit变换，即做“loga[x/(1-x)]”变换，这里的“a”通常为“e=2.718281828”。注意：x为数值型变量，其定义域为(0.0，1.0)。

POWER(x)：幂变换，即做“xa”变换。例如：希望做“x1.5”变换，关键词写为POWER(x/PARAMETER=1.5)。显然，当“PARAMETER=”后数值为“2”时，就是平方变换；为“-1”时，就是倒数变换；为“0.5”时，就是开平方根变换。

RANK(x)：秩变换。将变量x由小到大排序，再分别赋值为“1、2、3、4、5、……”。

1.2.3 非线性拟合变换

BOXCOX(x)：这是Box等[5]提出的变量变换方法，实际应用参见文献[6]。此变换只适用于回归分析中的“定量因变量”。

PBSPLINE(x)：这是非迭代惩罚B样条变换，使用时的特殊要求参见文献[1]。此变换只适用于回归分析中的“定量自变量”。

SMOOTH(x)：这是一种非迭代光滑样条变换，由Reinsch[7]提出的变量变换方法，使用时的特殊要求参见文献[1]。此变换只适用于回归分析中的“定量自变量”。

1.2.4 优化变换

优化变换就是采用迭代计算导出的变量变换方法。在SAS的“TRANSREG过程”中，涉及到以下六种优化变换方法，即：LINEAR(x)、MONOTONE(x)、MSPLINE(x)、OPSCORE(x)、SPLINE(x)和UNTIE(x)。以上六种优化变换在使用时都有具体要求，详见文献[1]，此处从略。

1.3 对定量变量进行其他变量变换

1.3.1 恒等变换[IDENTITY(x)]

恒等变换，就是没有改变变量的取值。通常情况下，就是“不做变换”。应注意：在使用SAS的“TRANSREG过程”时，写在“model语句”中的所有“因变量”和“自变量”之前必需要有“变量变换”的关键词。若不想对“x4-x10”进行任何变量变换，必须按如下的方式写：IDENTITY(x4-x10)。

使用此种变换，可以产生“交互项”，具体使用方法参见文献[1] ，此处从略。

1.3.2 迭代光滑样条变换[SSPLINE(x)]

这是对变量x进行迭代光滑样条变换，此变量变换方法通常不会使误差平方达到最小值。具体使用方法参见文献[1] ，此处从略。

2 实际问题与数据结构

沿用本期科研方法专题第一篇文章《提高回归模型拟合优度的策略(Ⅰ)——哑变量变换与其他变量变换》中的“实际问题与数据结构”[1]，此处从略。

3 解决问题的思路和做法

3.1 对多值名义自变量和多值有序自变量进行变量变换

3.1.1所需要的SAS程序

对“燃油种类(fuel)” 这个“6值名义自变量”进行“优化计分变换”；对“压缩比(cpratio)” 这个“5值有序自变量”进行“单调变换”。所需要的SAS程序如下：

ods graphics on;

title' Gasoline Example';

title2' Iteratively Estimate NOx, CpRatio, EqRatio, and Fuel';

* Fit the Nonparametric Model;

proc transreg data=sashelp.Gas solve test nomiss plots=all;

ods exclude where=(_path_ ? ' MV' );

model mspline(NOx / nknots=9) =

spline(EqRatio / nknots=9)

monotone(CpRatio) opscore(Fuel);

output out=aaa tdprefix=td tiprefix=ti;

run;

proc freq data=aaa;

tables cpratio ticpratio fuel tifuel;

run;

3.1.2 与所需变量变换有关的SAS输出结果

Compression RatioCpRatio频数百分比累积频数累积百分比7.59354.399354.399179.9411064.33122414.0413478.36152011.7015490.0618179.94171100.00

以上是“压缩比(cpratio)”的原始取值及其各水平的频数分布。

Compression Ratio TransformationtiCpRatio频数百分比累积频数累积百分比7.15982275949354.399354.3910.953020684179.9411064.3312.9445525662414.0413478.3614.201537262011.7015490.0617.433541388179.94171100.00

以上是“压缩比(cpratio)”经过“单调变换”后的取值及其各水平的频数分布。

由以上两部分输出结果可知：“单调变换”是将“多值有序变量”的水平做一一对应的变换，各水平出现的“频数”不会发生变化。

Fuel频数百分比累积频数累积百分比095.2695.2612514.623419.8829052.6312472.513137.6013780.1242212.8715992.985127.02171100.00

以上是“燃油种类(fuel)”的“6种水平代码(分别为0、1、2、3、4、5)”及其各水平的频数分布。

Fuel频数百分比累积频数累积百分比82rongas95.2695.2694%Eth2514.623419.88Ethanol9052.6312472.51Gasohol137.6013780.12Indolene2212.8715992.98Methanol127.02171100.00

以上是“燃油种类(fuel)”的“6种水平的真实含义”及其各水平的频数分布。

Fuel TransformationtiFuel频数百分比累积频数累积百分比1.3742357556127.02127.021.55720545762514.623721.641.59754088319052.6312774.274.209335677695.2613679.534.36641535932212.8715892.404.4654059829137.60171100.00

以上是“燃油种类(fuel)” 经过“优化计分变换”后的取值及其各水平的频数分布。

3.2 对定量自变量进行变量变换

对定量自变量可以进行“样条变换(spline)”“单调样条变换(mspline)”或“变量扩展变换(pspline)(即产生‘派生变量’，例如变量的平方项、立方项等)”。例如：对“eqratio”进行“样条变换”，可以写成spline(eqratio)或spline(eqratio/degree=3 nknots=0)。后一种写法涉及到两个参数，一是“degree=”，它是指“样条函数(通常是多项式)”中多项式的“次数”，“degree=3”代表“三次多项式”；二是“nknots=”，它是指“结点(或写成‘节点’)个数”，实际上就是“断点个数”。其具体含义是：在该定量变量的取值区间内，确定“几个断点(如nknots=9)”，于是，就将该区间划分成“10段”。在每一段上，拟合一个“多项式”。就整体而言，被称为“分段多项式(a piecewise polynomial)”。

3.3 对定量因变量进行变量变换

若需要变换的定量变量为“因变量”，除了可以进行“定量自变量”的某些变量变换(注意：“非迭代惩罚B样条变换”只能用于“定量自变量”)之外，还可以进行其他一些变量变换，如“BOX-COX变换(注意：该变换仅适用于‘定量因变量’)”等。

3.4 针对实际问题，寻找合适的变量变换方法

3.4.1寻找最优回归模型的策略

前面提及的“实际问题”涉及“定量因变量(nox)”“定量自变量(eqratio)”“多值有序自变量(cpratio)”和“多值名义自变量(fuel)”。在拟合多重回归模型的过程中，涉及到如何对上述4个变量进行“变量变换”。当然，对每个变量选取不同的“变量变换”方法，将会得到不同的拟合效果。下面将固定“多值名义自变量(fuel)”的变量变换方法为：优化计分变换，即“OPSCORE(fuel)”，对其他变量依次采取各种可能的变量变换，呈现出各种情况下回归模型的拟合优度，最终选择“拟合优度最好”的回归模型。

3.4.2不同变量变换方法组合下的回归模型拟合优度

在对“多值名义自变量(fuel)”做优化计分变换“OPSCORE(fuel)”的前提条件下，对其他变量依次采取各种可能的变量变换，对应的回归模型拟合优度见表1。

表1 在OPSCORE(fuel)的前提下对“nox”“eqratio”和“cpratio”进行不同变量变换后对应的回归模型的拟合优度

注：“Root MSE”代表“均方误差的平方根”，此值越小越好；“Nox_B”代表对“Nox”进行变量变换的方法，表中第3列和第4列符号代表的含义与“Nox_B”相同，此处从略

由表1可知：模型1和模型7的结果相同且拟合优度最好，对应的SAS过程步程序如下：

proc transreg data=sashelp.Gas solve test nomiss

plots=all;

ods exclude where=(_path_ ?' MV' );

model spline(NOx / nknots=9)

=spline(EqRatio / nknots=9)

monotone(CpRatio) opscore(Fuel);

run;

3.4.3 模型1的主要输出结果

由于“模型1”是一个“非参数模型”，只能给出总模型的有关信息和与“拟合优度”有关的结果，不能给出“回归系数”等信息。但可以以“图形”方式给出各变量变换的结果，以提示对不同变量采取什么变量变换方法最有效。下面先给出与“拟合优度”有关的结果：

Root MSE0.30935R-Square0.9586Dependent Mean2.34593Adj R-Sq0.9527Coeff Var13.18661

表1中的第1行就是摘录了以上的结果。

在前面给出的“SAS过程步”的“MODEL语句”中，对定量因变量(nox)、定量自变量(EqRatio)、多值有序自变量(CpRatio)和多值名义自变量(Fuel)分别做了“样条变换”“样条变换”“单调变换”和“优化计分变换”，变换的结果用“图形”呈现出来，见图1。

图1 基于MODEL语句中的要求对4个变量做的变换结果

在图1中，左上方一图表明：定量因变量(nox)呈现出“对数”变化趋势，提示可对其进行“对数变换”；右上角一图表明：定量自变量(EqRatio)呈现出“二次抛物线”变化趋势，提示可对其进行“二次多项式变换”；左下角一图表明：多值有序自变量(CpRatio)呈现出近似“直线”变化趋势，提示可对其进行“恒等变换(即不做变换)”；右下角一图表明：多值名义自变量(Fuel)呈现出“两种级别”，其中，水平代码为“1、2、5”的燃料种类对结果的影响数量大约在“1与2”之间；而水平代码为“0、3、4”的燃料种类对结果的影响数量大约在“4与5”之间，纵轴上的“数量”就是“优化计分”的结果。

基于以上的“非参数多重非线性回归分析结果(以图1反映其变量变换的效果)”，可以构建参数多重非参数回归分析模型如下：

log(nox) = b0+b1*EqRatio+b2*EqRatio**2+b3*CpRatio+Sum b(j)*Fuel(j)+Error

此模型的含义是：对定量因变量(nox)进行自然对数变换，对定量自变量(EqRatio)进行二次多项式变换，对多值有序自变量(CpRatio)进行恒等变换，而对多值名义自变量(Fuel)进行优化计分变换并将其6个计分值[Fuel(j)]与其回归系数[b(j)]分别相乘后求和(j=0、1、2、3、4、5)(注意：相当于把“6值名义自变量”视为6个新变量，就有6个回归系数；但它们又属于同一个多值名义变量，因此，其自由度为6-1=5，在本质上相当于是5个哑变量)。

3.4.4 构建参数多重非线性回归模型

采用SAS拟合上述参数多重非线性回归模型所需要的SAS过程步程序如下：

title2' Now fit log(nox) = b0 + b1*EqRatio + b2*EqRatio**2 +';

title3' b3*CpRatio + Sum b(j)*Fuel(j) + Error';

*-Fit the Parametric Model Suggested by the Nonparametric Analysis-;

proc transreg data=sashelp.Gas solve ss2 short

nomiss plots=all cldetail;

model log(nox) = pspline(EqRatio / deg=2)

identity(CpRatio) opscore(Fuel);

run;

3.4.5 参数多重非线性回归模型输出结果

Univariate ANOVA Table Based on the Usual Degrees of FreedomSourceDFSum of SquaresMean SquareFPr > FModel879.338389.917298213.09<0.0001Error1607.446590.046541Corrected Total16886.78498

以上是总模型的假设检验结果，F=213.09，P<0.0001，表明总模型具有统计学意义。

Root MSE0.21573R-Square0.9142Dependent Mean0.63130Adj R-Sq0.9099Coeff Var34.17294

以上是拟合优度评价结果：均方误差平方根为0.21573，R2为0.9142，调整R2为0.9099，相对于表1中“模型1”的三个对应的数值(0.30935、0.9586、0.9527)，均方误差平方根略微变小了一点，然而，R2和调整R2的数值却下降得比较多(因为模型中自变量的项数减少得很多，现在模型的自由度df=8；而模型1的df=21)。

Univariate Regression Table Based on the Usual Degrees of FreedomVariableDFCoefficientType II Sum of SquaresMean SquareFPr > FLabelIntercept1-15.27464957.133857.13381227.60<0.0001InterceptPspline.EqRatio_1135.10291462.747862.74781348.22<0.0001Equivalence Ratio 1Pspline.EqRatio_21-19.38646864.643064.64301388.94<0.0001Equivalence Ratio 2Identity(CpRatio)10.0320581.44451.444531.04<0.0001Compression RatioOpscore(Fuel)50.1583885.56191.112423.90<0.0001Fuel

以上为回归模型的回归系数与假设检验结果(因输出结果过宽，将其中参数的置信区间等信息省略掉了)。其中，第2、3两行上分别为“定量自变量(EqRatio)”的“一次项”与“二次项”的计算结果；第4行上为“多值有序自变量(CpRatio)”的计算结果；而第5行上为“多值名义自变量(Fuel)”的计算结果，具有5个自由度，但只有一个回归系数。

基于上述回归模型计算出定量因变量的预测值作为横坐标的数值，其原始观测值作为纵坐标的数值，绘制出散布图，以直观的方式呈现模型对资料的拟合效果。见图2。

图2 反映因变量(nox)的观测值与预测值的散布图

由图2可知：此回归模型对资料的拟合效果比较令人满意。

4 总 结

4.1 本文方法的小结

本文对“多值名义自变量”进行“优化计分变换(Opscore)”，取代了经典统计学中常规的“哑变量变换”。在此基础上，对“定量因变量(nox)”分别进行了“样条变换(Spline)”“单调样条变换(Mspline)”和“Box-Cox变换”三种变量变换；对“定量自变量(EqRatio)”分别进行了“样条变换(Spline)”和“单调样条变换(Mspline)”两种变量变换；对“多值有序自变量(CpRatio)”分别进行了“单调变换(Monotone)”和“优化计分变换(Opscore)”。从而，获得“最优模型”的拟合优度评价指标为“均方误差平方根=0.30935、R2=0.9586、调整R2=0.9527”。由于此模型相对比较复杂(自变量有21项且写不出具体的回归系数)；简化后的参数多重非线性回归模型仅含8个自变量(注：包括派生变量)，R2为0.9142，调整R2为0.9099。

4.2 其他方法的回顾

在本期科研方法专题的前三篇文章中，分别对“多值名义自变量”进行“哑变量变换”“算术均值变换”和“校正均值变换”，对“定量因变量(nox)”进行了“不变换”“自然对数变换”“平方根变换”“倒数变换”“指数变换”和“Logistic变换”；对“定量自变量(EqRatio)”和“多值有序自变量(CpRatio)(被视为‘定量的’)”引入了“派生变量”。还在模型中假定“包含截距项”和“不含截距项”两种情形下，分别采取“前进法”“后退法”和“逐步法”筛选自变量。在前三篇文章中的每一篇中，都从大约72个模型中选出了24个“最优模型”且以“模型24”为“最佳模型”。

4.3 四组方法的总结

“四组方法”指本期科研方法专题中四篇文章所介绍的方法，即分别对“多值名义自变量”进行“哑变量变换”“算术均值变换”“校正均值变换”和“优化计分变换”。在此基础上，再对其他变量采用多种变量变换方法，最后以“拟合优度评价指标”的取值为判断标准，总结于下表2。

表2 四篇文章中“最佳”回归模型拟合优度评价指标汇总

注：前三篇文章原先给出的是“均方误差(MSE)”，分别为“0.00076”“0.00060”和“0.00061”，将它们分别开平方根，得到“0.02757”“0.02449”和“0.02470”。由表2可知，前三篇文章回归模型的拟合效果非常接近，均优于第4篇文章回归模型的拟合效果；然而，第一篇文章回归模型中保留了“部分哑变量”，严格来说，它不是非常理想的结果

由此可以得出如下结论：在对“定量因变量”构建多重非线性回归模型中，对“多值名义自变量”是采取“哑变量变换”“优化计分变换”还是“均值或校正均值变换”，对结果的影响都不是特别大，关键在于以下四点：第一，应对“定量因变量”“定量自变量”和“多值有序自变量”采取合适的变量变换；第二，应尽可能引入较多的“派生变量”；第三，应假定“模型中不含截距项”；第四，应尽可能多采取一些筛选自变量的策略，如前进法、后退法和逐步法。

最后还需要注意：引入派生变量后获得的“最佳”回归模型通常具有“严重多重共线性”，若最终的回归模型中的某些回归系数的“正负号”与专业知识不符合，此时，再基于“最佳回归模型”所确定的“自变量组合”进行“岭回归分析”。从而获得满意的结果[4]。