提高回归模型拟合优度的策略(Ⅰ)
——哑变量变换与其他变量变换
2019-03-29胡良平
胡良平
(1.军事医学科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029
1 变量变换的必要性及变换方法
1.1 多值名义变量的变量变换
1.1.1 选择合适变量变换方法的必要性
在进行回归分析时,若自变量中有“多值名义变量”(如职业、血型、仪器品牌等),其具体的“表现或水平”不能用“文字”或“字母”表示,也不能简单地赋值“1、2、3……”前者无法参与统计计算,而后者将会导致计算结果错误。那么,究竟应该对“多值名义变量”进行什么样的变量变换呢?本文将介绍常规做法,即进行“哑变量变换”。
在回归分析中应如何处置“多值有序变量”?在统计学上,人们认为:直接采用多值有序变量各水平的数值为其取值,例如:假定x代表“肿瘤分级”,依据临床专业知识,已知它可以分为五级,于是,认为 x的取值就是“1、2、3、4、5”。依据基本常识可知,这样的做法是不妥的。因为当肿瘤处于不同等级,其对结果的影响可能不是“线性关系”,很可能是较复杂的“非线性关系”。因此,应将“多值有序自变量”视为“多值名义自变量”,采用合适的变量变换方法。
1.1.2 对多值名义变量进行“哑变量变换”
所谓哑变量变换,就是将一个具有k个水平的多值名义变量转换成(k-1)个新变量,每个新变量都是一个“二值变量(即仅有两个不同取值的变量)”。这些新变量像“哑巴”一样,其中的每一个都携带着原变量的一部分信息,在计算中发挥一定的作用,但又不能完全取代原变量,故它们都被形象地称为“哑变量”。
实施哑变量变换的方法是:选择一个频率高的水平作为“基准水平”,其他水平都与该基准水平作比较而产生一个“比较变量”(即哑变量)。例如:在ABO血型系统中,假定在样本资料中属于O型血的人数最多,就可以以“O型血的人”为“基准水平”,其他三种血型的人相对于O型血的人分别产生一个“哑变量”。简化形式呈现如下:

个体编号血型XA|OXB|OXAB|O1A1002B0103AB0014O000
在上面的简化形式中,“XA|O、XB|O、XAB|O”这三个变量都是与“血型”这个4值名义变量对应的“哑变量”,它们分别代表“是否为A型血”“是否为B型血”和“是否为AB型血”。
1.1.3 对多值名义变量进行“其他变量变换”
在进行回归分析中,上面的“哑变量变换”已经成为统计学界处置“多值名义自变量”的“金标准”。是否还有更合理的“变量变换”方法可以取代“哑变量变换”呢?此问题将在本期“科研方法专题”的另三篇文章中深入讨论。
1.2 定量变量的变量变换
1.2.1 选择合适变量变换方法的必要性
通常情况下,人们在进行回归分析时,对于定量的自变量和/或因变量不作任何变换。然而,由基本常识可知,前述做法是不切实际的,通常情况下,效果是不够好的。因为变量之间的关系往往是错综复杂的,它们之间永远以“一次方”形式存在联系的可能性是非常罕见的。因变量Y可能与某个自变量之间是抛物线关系、指数曲线关系或对数曲线关系;因变量Y本身可能偏离正态分布很远,而很多统计模型要求因变量必须服从正态分布。因此,需要对定量因变量作合适的变量变换,以使其符合特定统计模型的基本要求;需要对某些定量自变量作合适的变量变换,以更真实地呈现其与定量因变量之间的变化趋势。
1.2.2 对定量自变量进行两方面的变量变换
第一方面的变量变换就是对某定量自变量作了某种变量变换后,丢弃原先的那个自变量,而仅采用变换后的变量。例如:建模时,只用“log(x1)”,而丢弃“x1”。第二方面的变量变换就是不仅用变换后的变量,还保留未变换的原变量。这样做的结果会使自变量的数目大大增加,常称为产生“派生变量”。例如:假定有10个定量变量,可以给它们都取对数变换,就会增加10个新变量;也可以对10个变量进行平方变换或平方根变换;还可以基于10个定量变量产生交叉乘积项等。
1.2.3 对定量因变量进行变量变换
在通常情况下,人们进行的是“一元多重回归分析”,因此,若对定量因变量进行变量变换,在回归建模时,只使用变换后的因变量,而不会同时使用原先的“因变量”与变换后的因变量(因为这样做已经把“一元”问题转变成“二元”问题了)。
何时需要对定量因变量进行变换呢?通常在以下两种情况之一:其一,已知因变量与自变量之间呈某种函数关系,就选择相应的变量变换方法。例如:当因变量与自变量之间呈“指数函数”变化关系时,就可以对因变量取对数变换;其二,当定量因变量(严格地说,应该是模型的误差项)偏离正态分布很远时,需要选择一种合适的变量变换方法,目的是使变换后的因变量服从模型所要求的某种概率分布,如正态分布、指数分布或威布尔分布等。
2 实际问题与数据结构
2.1 实际问题
研究者关心的定量结果变量为“氧化氮释放量(nox)”,该定量指标的数值测自单缸发动机。已知影响因素有:燃油种类(fuel)、压缩比(cpratio)和等值比(eqratio)。其中,燃油种类(fuel)是多值名义变量,而氧化氮释放量(nox)、压缩比(cpratio)和等值比(eqratio)都是计量变量。该资料来自SAS软件中的“帮助”数据库,数据集名为:sashelp.gas。
试以“氧化氮释放量(nox)”为因变量,以“燃油种类(fuel)、压缩比(cpratio)和等值比(eqratio)”为自变量,创建一元多重回归模型。
【说明】该实际问题和对应的数据来源于“SAS/STAT的TRANSREG过程中的样例及SASHELP数据库,其数据集名为sashelp.gas”[1]。
2.2 数据结构
利用以下SAS程序可以显示该例的数据结构:
proc print data=sashelp.gas;
run;
【燃油资料的数据结构】
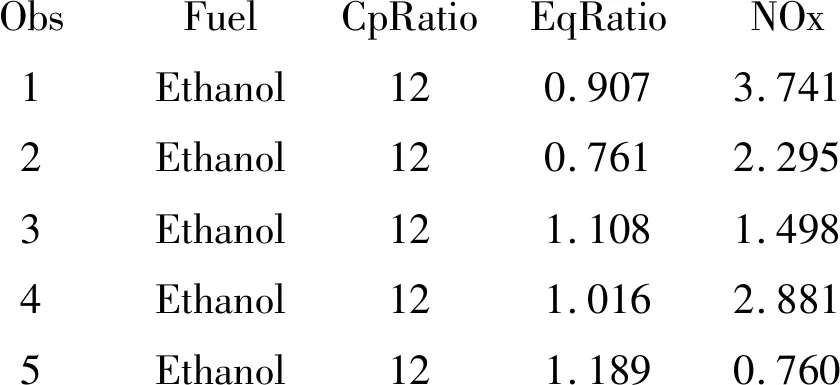
ObsFuelCpRatioEqRatioNOx1Ethanol120.9073.7412Ethanol120.7612.2953Ethanol121.1081.4984Ethanol121.0162.8815Ethanol121.1890.760
以上显示出数据集的前5个观测,全部资料共171个观测。其中,在结果变量nox上有两个缺失值。
利用如下SAS程序可以显示三个自变量(一个为多值名义自变量、一个为多值有序自变量、一个为定量自变量)及定量结果变量(nox)的频数分布情况:
proc freq data=sashelp.gas;
tables fuel eqratio cpratio nox;
run;
【燃油种类的频数分布】

Fuel频数百分比累积频数累积百分比82rongas95.2695.2694%Eth2514.623419.88Ethanol9052.6312472.51Gasohol137.6013780.12Indolene2212.8715992.98Methanol127.02171100.00
以上结果表明:共有6种燃油,其中,频数最多的是“Ethanol”,涉及此种燃油的观测共有90个。
【压缩比的频数分布】
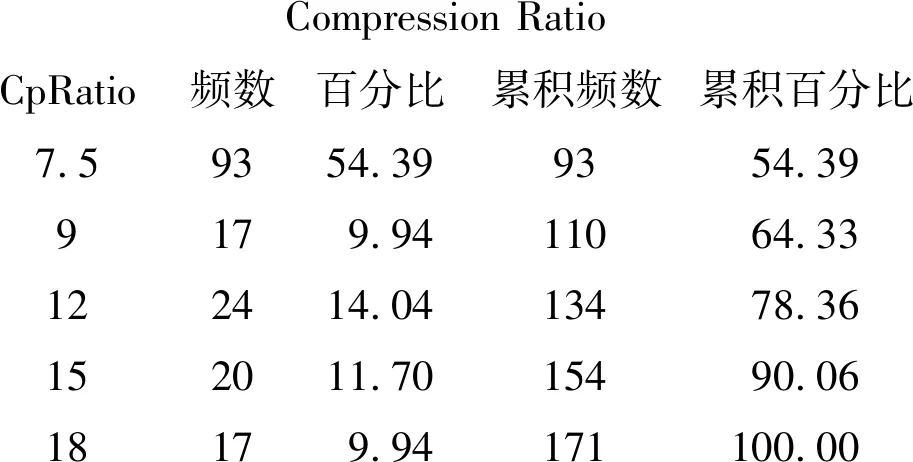
Compression RatioCpRatio频数百分比累积频数累积百分比7.59354.399354.399179.9411064.33122414.0413478.36152011.7015490.0618179.94171100.00
以上结果表明:压缩比只有5种,属于“多值有序”变量(注意:以下简称为“定量变量”)。其中,频数最多的是“7.5”,涉及此种压缩比的观测共有93个。
等值比(eqratio)与氧化氮释放量(nox)的取值都很多,其频数分布表此处从略;但利用下面的SAS程序可以显示这两个变量的频数分布直方图,同时,还可以对它们进行正态性检验:
proc univariate data=sashelp.gas normal;
var eqratio nox;
histogram eqratio nox/normal;
run;
【等值比的正态性检验结果】

正态性检验检验统计量PShapiro-WilkW0.969774Pr
以上结果表明:等值比不服从正态分布。
等值比的频数分布直方图见图1。由图1可知,等值比呈“负偏态分布”
【氧化氮释放量的正态性检验结果】

正态性检验检验统计量PShapiro-WilkW0.945485Pr
以上结果表明:氧化氮释放量不服从正态分布。
氧化氮释放量的频数分布直方图见图2。由图2可知:氧化氮释放量呈“正偏态分布”。
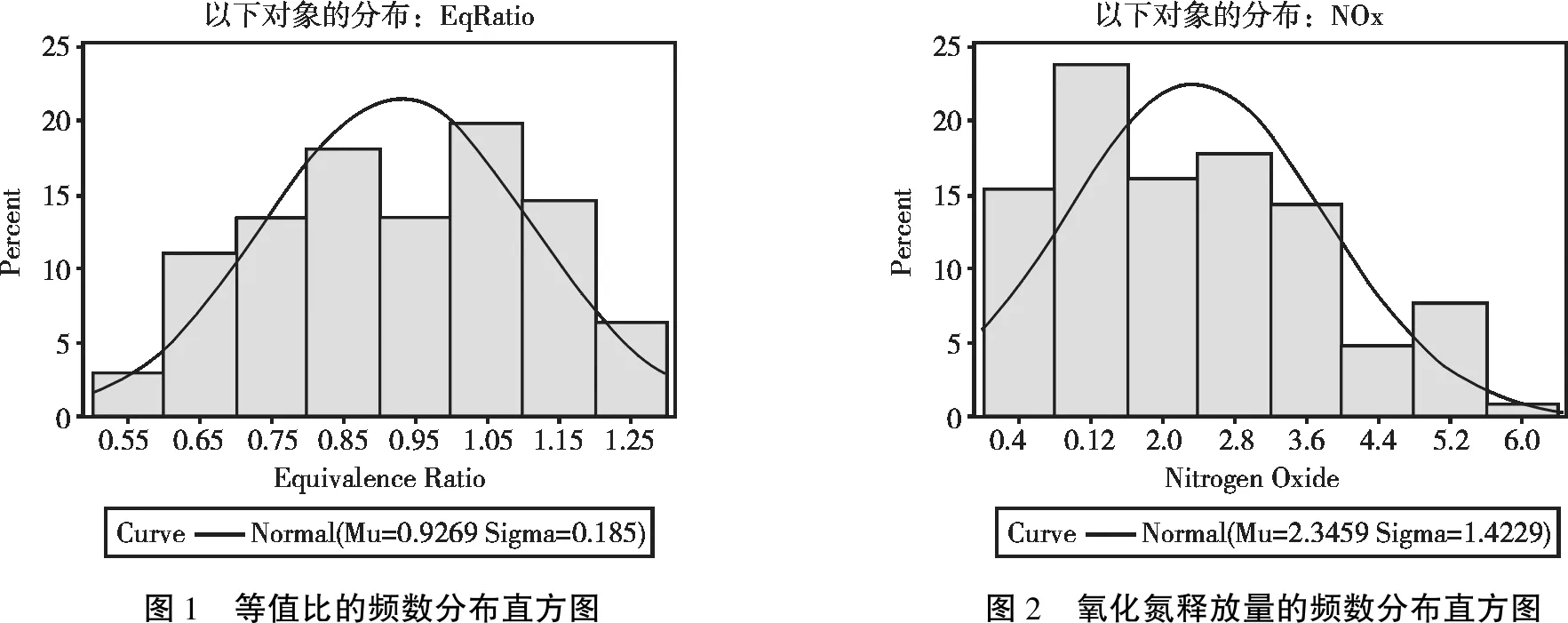
图1 等值比的频数分布直方图 图2 氧化氮释放量的频数分布直方图
3 变量变换,为回归建模做准备工作
3.1 对“燃油种类(fuel)”这个6值名义自变量进行哑变量变换[2]
选择出现频数最多的水平“Ethanol”为“基准”,产生5个哑变量:g1到g5。实现此任务的SAS程序如下:
data a1;
set sashelp.gas;
g1=0;g2=0;g3=0;g4=0;g5=0;
if fuel=' 82rongas' then g1=1;
else if fuel=' 94%Eth' then g2=1;
else if fuel=' Gasohol' then g3=1;
else if fuel=' Indolene' then g4=1;
else if fuel=' Methanol' then g5=1;
run;
g1到g5分别代表:“是否为82rongas燃油”“是否为94%Eth燃油”“是否为Gasohol燃油”“是否为Indolene燃油”和“是否为Methanol燃油”。
3.2 产生派生变量[3]
在数据集a1基础上增加由定量自变量派生出来的13个新变量,产生数据集a2。SAS程序如下:
data a2;
set a1;
x1=eqratio**2;x2=eqratio*cpratio;
x3=cpratio**2;x4=x1*eqratio;
x5=x3*cpratio;x6=x1*cpratio;
x7=x3*eqratio;x8=sqrt(eqratio);
x9=sqrt(cpratio);x10=log(eqratio);
x11=log(cpratio);x12=exp(eqratio);
x13=exp(cpratio);
run;
【说明】cpratio和eqratio是资料中两个原始的定量自变量;x1、x4、x8、x10、x12分别是“eqratio”的平方变换、立方变换、平方根变换、自然对数变换和指数变换的结果;x3、x5、x9、x11、x13分别是“cpratio”的平方变换、立方变换、平方根变换、自然对数变换和指数变换的结果;x2是“eqratio”与“cpratio”的交叉乘积项;x6是“eqratio”的平方项与“cpratio”的交叉乘积项;而x7是“cpratio”的平方项与“eqratio”的交叉乘积项。
3.3 对定量因变量进行5种变量变换
在数据集a2基础上同时增加定量因变量的对数变换y1、平方根变换y2、指数变换y3、倒数变换y4和Logistic变换y5,产生数据集a3。SAS程序如下:
data a3;
set a2;
y1=log(nox);y2=sqrt(nox);y3=exp(nox);
y4=1/nox;y5=exp(nox)/(1+exp(nox));
run;
4 以“哑变量变换”为基础的回归建模
4.1 回归建模策略概述
对一个“多值名义自变量”采取“哑变量变换”,以其为基础,再分别选取定量因变量(nox)的6种不同“表现”为每次建模的“因变量”,并对定量自变量在“不做变量变换”和“引入13个派生变量”且分别在回归模型中假定“包含截距项”与“不含截距项”的条件下,采取“前进法”“后退法”和“逐步法”筛选自变量。
4.2 定量因变量(nox)的6种不同“表现”
定量因变量(nox)的6种不同“表现”分别是:①定量因变量(nox),即对“定量因变量(nox)”不做变量变换;②定量因变量[y1=log(nox)],即对“定量因变量(nox)”做自然对数变换;③定量因变量[y2=SQRT(nox)],即对“定量因变量(nox)”做平方根变换;④定量因变量[y3=exp(nox)],即对“定量因变量(nox)”做指数变换;⑤定量因变量(y4=1/nox),即对“定量因变量(nox)”做倒数变换;⑥定量因变量{y5=exp(nox)/[1+exp(nox)]},即对“定量因变量(nox)”做Logistic变换。
4.3 在定量因变量(nox)每种“表现”下找出4个“最优回归模型”
在定量因变量(nox)每种“表现”且分别在定量自变量“不做变换”与“引入派生变量”的条件下,再在回归模型中假定“包含截距项”与“不含截距项”时,分别采取“前进法”“后退法”和“逐步法”筛选自变量。这实际上就有“2×2×3=12”个回归模型,它们分属于4种情形:①“定量自变量不做变换”且假定“包含截距项”;②“定量自变量不做变换”且假定“不含截距项”;③“定量自变量做变换”且假定“包含截距项”;④“定量自变量做变换”且假定“不含截距项”。每种情形都涉及3种筛选自变量的方法,最多有3种不同的回归模型,从中选取一个拟合最好的回归模型。
所以,在每种特定的因变量条件下,就对应着4个“最优回归模型”;故在因变量的6种条件下,一共有24个“最优回归模型”。见表1。
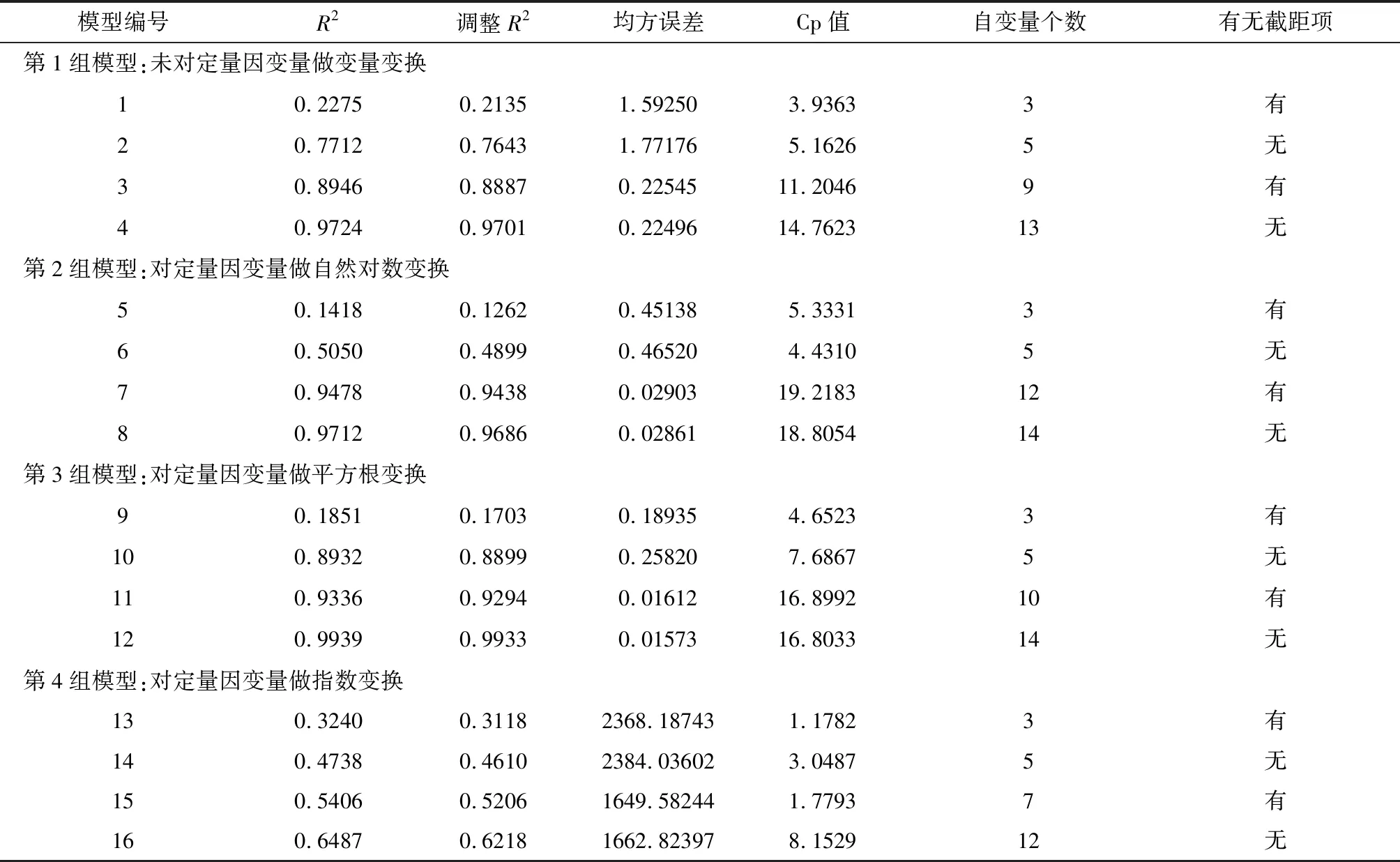
表1 反映24个多重回归模型拟合优度的计算结果
续表1:
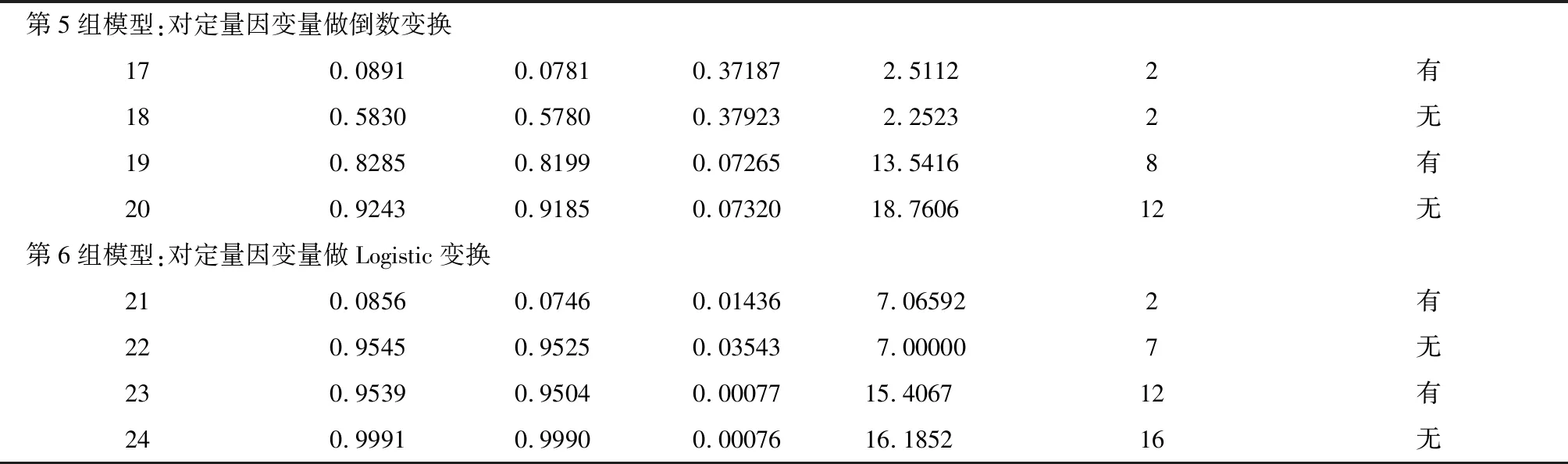
第5组模型:对定量因变量做倒数变换170.0891 0.0781 0.37187 2.5112 2 有180.58300.5780 0.37923 2.2523 2 无190.8285 0.8199 0.0726513.5416 8 有200.9243 0.9185 0.0732018.7606 12 无第6组模型:对定量因变量做Logistic变换210.0856 0.0746 0.01436 7.06592 2 有220.9545 0.9525 0.03543 7.00000 7 无230.9539 0.9504 0.0007715.4067 12 有240.9991 0.9990 0.0007616.1852 16 无
注:第1组模型对应的因变量为“氧化氮释放量(nox)”;第2组模型对应的因变量为“氧化氮释放量的自然对数变换结果(y1)”;第3组模型对应的因变量为“氧化氮释放量的平方根变换结果(y2)”;第4组模型对应的因变量为“氧化氮释放量的指数变换结果(y3)”;第5组模型对应的因变量为“氧化氮释放量的倒数变换结果(y4)”;第6组模型对应的因变量为“氧化氮释放量的Logistic变换结果(y5)”
5 拟合优度评价标准与评价结果
5.1 回归模型拟合优度高低的评价标准
一般来说,当模型中包含的自变量数目相等且都包含截距项或都不含截距项时,R2值越大越好;此时,Cp值越接近自变量个数越好;当保留在模型中的自变量个数相差较多时,在前述判断方法基础上,再加上“均方误差”(越小越好)和“调整R2”(越大越好),则更好。
5.2 基于“哑变量变换与其他变量变换”回归建模效果的评价
5.2.1 第1组模型的拟合效果评价
第1组模型对应的因变量为“氧化氮释放量”,模型1与模型2都是基于“5个哑变量加上2个定量自变量”进行变量筛选,其区别在于模型1假定包含截距项,而模型2假定不含截距项;模型3与模型4都是基于“5个哑变量加上2个定量自变量及其13个派生变量”进行变量筛选,其区别在于模型3假定包含截距项,而模型4假定不含截距项。由表1中前4行结果可知:模型2优于模型1、模型4优于模型3,即在相同情况下,假定不含截距项的拟合结果优于假定包含截距项的拟合结果;进一步比较可知:模型4优于模型2,即引入派生变量的拟合结果优于不引入派生变量的拟合结果。
5.2.2 第2组模型的拟合效果评价
第2组模型对应的因变量为“氧化氮释放量的自然对数变换结果(y1)”,模型5与模型6都是基于“5个哑变量加上2个定量自变量”进行变量筛选,其区别在于模型5假定包含截距项,而模型6假定不包含截距项;模型7与模型8都是基于“5个哑变量加上2个定量自变量及其13个派生变量”进行变量筛选,其区别在于模型7假定包含截距项,而模型8假定不包含截距项。由表1中第5~8行结果可知:模型6优于模型5、模型8优于模型7,即在相同情况下,假定不含截距项的拟合结果优于假定包含截距项的拟合结果;进一步比较可知:模型8优于模型6,即引入派生变量的拟合结果优于不引入派生变量的拟合结果。
5.2.3 第3组模型的拟合效果评价
第3组模型对应的因变量为“氧化氮释放量的平方根变换结果(y2)”,模型9与模型10都是基于“5个哑变量加上2个定量自变量”进行变量筛选,其区别在于模型9假定包含截距项,而模型10假定不包含截距项;模型11与模型12都是基于“5个哑变量加上2个定量自变量及其13个派生变量”进行变量筛选,其区别在于模型11假定包含截距项,而模型12假定不包含截距项。由表1中第9~12行结果可知:模型10优于模型9、模型12优于模型11,即在相同情况下,假定不含截距项的拟合结果优于假定包含截距项的拟合结果;进一步比较可知:模型12优于模型10,即引入派生变量的拟合结果优于不引入派生变量的拟合结果。
5.2.4 第4组模型的拟合效果评价
第4组模型对应的因变量为“氧化氮释放量的指数变换结果(y3)”,模型13与模型14都是基于“5个哑变量加上2个定量自变量”进行变量筛选,其区别在于模型13假定包含截距项,而模型14假定不包含截距项;模型15与模型16都是基于“5个哑变量加上2个定量自变量及其13个派生变量”进行变量筛选,其区别在于模型15假定包含截距项,而模型16假定不包含截距项。由表1中第13~16行结果可知:模型14优于模型13、模型16优于模型15,即在相同情况下,假定不含截距项的拟合结果优于假定包含截距项的拟合结果;进一步比较可知:模型16优于模型14,即引入派生变量的拟合结果优于不引入派生变量的拟合结果。
5.2.5 第5组模型的拟合效果评价
第5组模型对应的因变量为“氧化氮释放量的倒数变换结果(y4)”,模型17与模型18都是仅基于“3个定量自变量”进行变量筛选,其区别在于模型17假定包含截距项,而模型18假定不包含截距项;模型19与模型20都是基于“3个定量自变量及其18个派生变量”进行变量筛选,其区别在于模型19假定包含截距项,而模型20假定不包含截距项。由表1中第17~20行结果可知:模型18优于模型17、模型20优于模型19,即在相同情况下,假定不含截距项的拟合结果优于假定包含截距项的拟合结果;进一步比较可知:模型20优于模型18,即引入派生变量的拟合结果优于不引入派生变量的拟合结果。
5.2.6 第6组模型的拟合效果评价
第6组模型对应的因变量为“氧化氮释放量的Logistic变换结果(y5)”,模型21与模型22都是仅基于3个定量自变量进行变量筛选,其区别在于模型21假定包含截距项,而模型22假定不包含截距项;模型23与模型24都是基于3个定量自变量及其18个派生变量进行变量筛选,其区别在于模型23假定包含截距项,而模型24假定不包含截距项。由表1中第21~24行结果可知:模型22优于模型21、模型24优于模型23,即在相同情况下,假定不含截距项的拟合结果优于假定包含截距项的拟合结果;进一步比较可知:模型24优于模型22,即引入派生变量的拟合结果优于不引入派生变量的拟合结果。
5.2.7各组模型中最优模型拟合优度总评价
从以上的“评价结果”可知:模型4、模型8、模型12、模型16、模型20和模型24分别是从6组模型中挑选出来的“最优模型”,现将它们从表1中摘录出来,以便直观比较和判断。见表2。
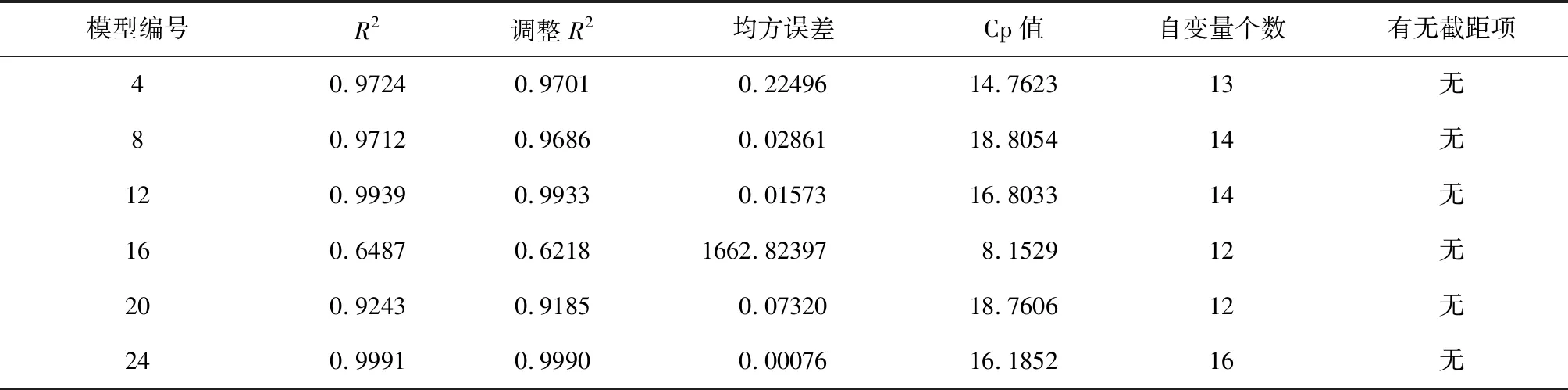
表2 各组挑选出来的6个“最优”多重回归模型拟合优度的计算结果
由表2可知:模型24是6个“最优”模型中“最佳”的。该模型的因变量为“氧化氮释放量(nox)的Logistic变换结果(y5)”,从全部(5+2+13=20个)自变量中筛选出了16个具有统计学意义的自变量,模型中不含截距项。具体计算结果如下:

方差分析源自由度平方和均方FPr > F模型16126.039047.8774410431.6<0.0001误差1530.115540.00075515未校正合计169126.15458
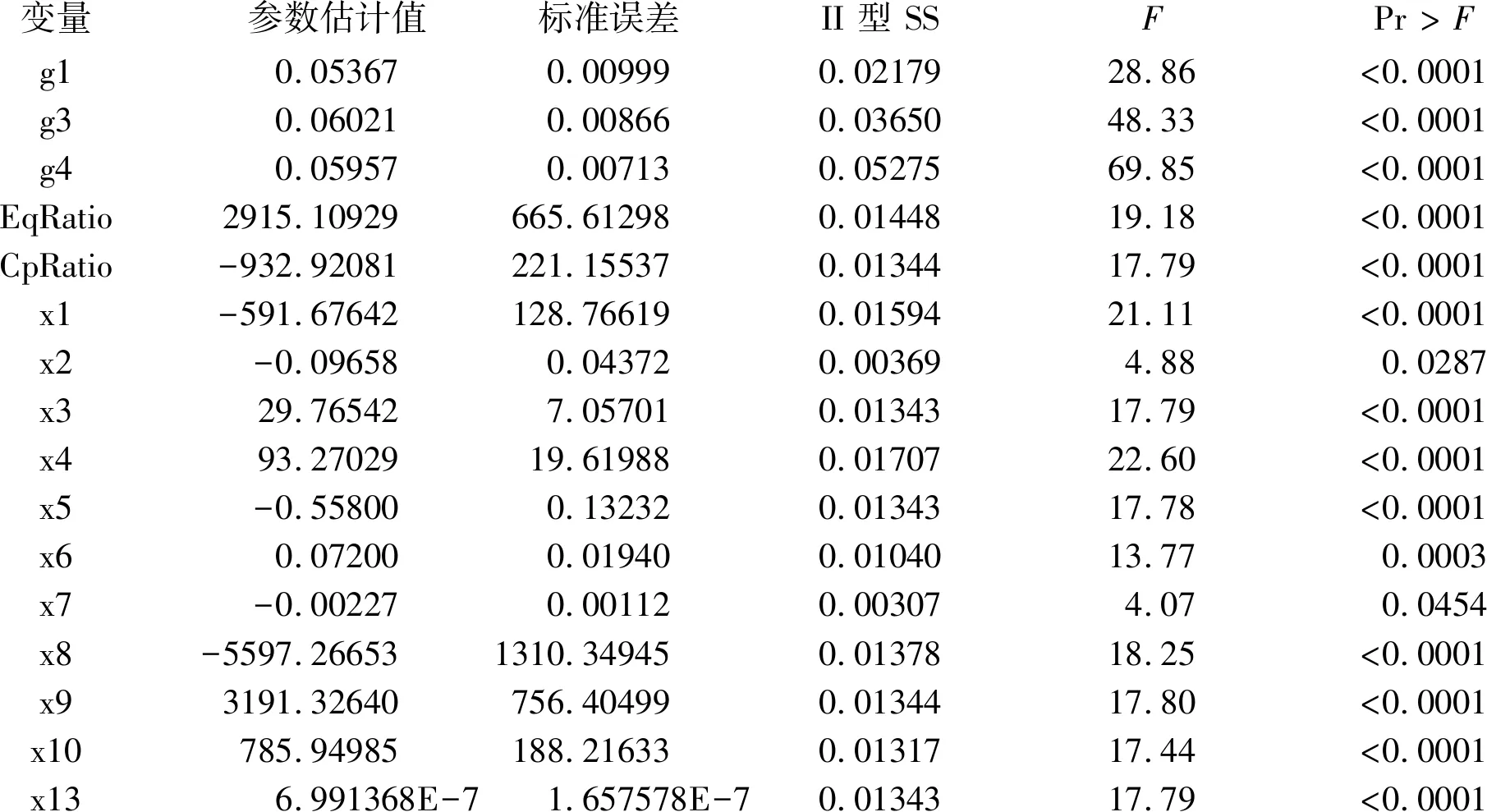
变量参数估计值标准误差II 型 SSFPr > Fg10.053670.009990.0217928.86<0.0001g30.060210.008660.0365048.33<0.0001g40.059570.007130.0527569.85<0.0001EqRatio2915.10929665.612980.0144819.18<0.0001CpRatio-932.92081221.155370.0134417.79<0.0001x1-591.67642128.766190.0159421.11<0.0001x2-0.096580.043720.003694.880.0287x329.765427.057010.0134317.79<0.0001x493.2702919.619880.0170722.60<0.0001x5-0.558000.132320.0134317.78<0.0001x60.072000.019400.0104013.770.0003x7-0.002270.001120.003074.070.0454x8-5597.266531310.349450.0137818.25<0.0001x93191.32640756.404990.0134417.80<0.0001x10785.94985188.216330.0131717.44<0.0001x136.991368E-71.657578E-70.0134317.79<0.0001
输出以上结果的“SAS过程步程序”如下:
/*模型24:R2=0.9991,调整R2=0.9990,MSE=0.00075515,Cp=16.1852,niv=16,无截距项*/
proc reg data=a3;
model y5=g1-g5 eqratio cpratio x1-x13/noint
selection=backward sls=0.05 r;
/*模型24*/
run;
应注意:全部哑变量共有5个(它们之间不是互相对立的),采用筛选自变量的方法,保留下来其中的3个。严格地说,由一个多值名义自变量产生的全部哑变量应当同时被保留在回归模型中或同时被排除出回归模型,但这两种结局都存在局限性;而将有关联性的5个哑变量视为“独立”的,根据假设检验结果保留其中的3个,这个结果也存在弊端。如何更妥善地处置“多值名义自变量”,将在本期科研方法专题后续文章中继续讨论。
