基于磁记忆技术对含缺陷焊缝的疲劳试验

任尚坤，祖瑞丽

南昌航空大学 无损检测技术教育部重点实验室，南昌 330063

金属磁记忆检测技术是一种新型且绿色环保的无损检测技术，是通过对铁磁试件上以应力集中为特征的危险区域的自发漏磁场进行分析[1-3]，对受载试件的损伤程度进行早期诊断，从而预防灾难事故的发生。磁记忆检测技术兴起以来[4-5]，国内外很多专家学者都对它做了大量的理论研究和仪器开发，取得了卓越的成就[6]，其中针对焊缝构件的磁记忆检测技术方面也进行了相关理论和试验方面的研究[7-8]。刘红光等[9]对焊缝缺陷处的磁记忆信号变化规律进行研究，建立了地磁场下焊缝的磁偶极子模型，对焊缝缺陷进行评价；邱新杰等[10-12]通过对漏磁场特性的研究，以焊接裂纹金属磁记忆信号的小波包能量为特征建立了神经网络系统，对焊缝中是否含有裂纹等缺陷进行智能识别；Dubov等[13-14]将磁记忆检测技术应用在电力工程和汽轮机部件的焊接钢结构的初始阶段预防上，评估了焊接接头在热处理前后的应力应变状态的不均匀性。

焊接缺陷的种类、大小、位置和方向等都会对焊接构件的疲劳强度造成一定影响[15]。焊接缺陷减小了焊接结构所承载的有效面积，进而在缺陷附近产生应力集中[16]。本文在学者们研究的基础上，针对焊接结构中常见的几种焊接缺陷展开研究。对含有隐形损伤的焊接构件进行射线检测、疲劳试验和正交磁记忆信号测量，分析疲劳循环应力作用下缺陷焊件的磁信号特征，并尝试建立以磁场矢量特征为损伤参量的焊缝疲劳损伤模型，进而对焊缝的疲劳寿命进行预估，为磁记忆检测技术在焊接缺陷定量评价的进一步研究提供参考依据。

1 试验材料及方法

1.1 试验材料

试验采用40Cr调质钢。试件结构尺寸为40 mm×200 mm×4 mm，焊缝宽5 mm，如图1所示。焊接方法为氩弧焊，焊机为WSME-315，所用焊条为直径1.8 mm的A201钛型药皮的低碳Cr18Ni12Mo2不锈钢焊条。在焊接过程中，通过控制焊接电流的大小和焊接速度的快慢来预置未焊透和夹渣等缺陷，从而预置不同的焊接质量。

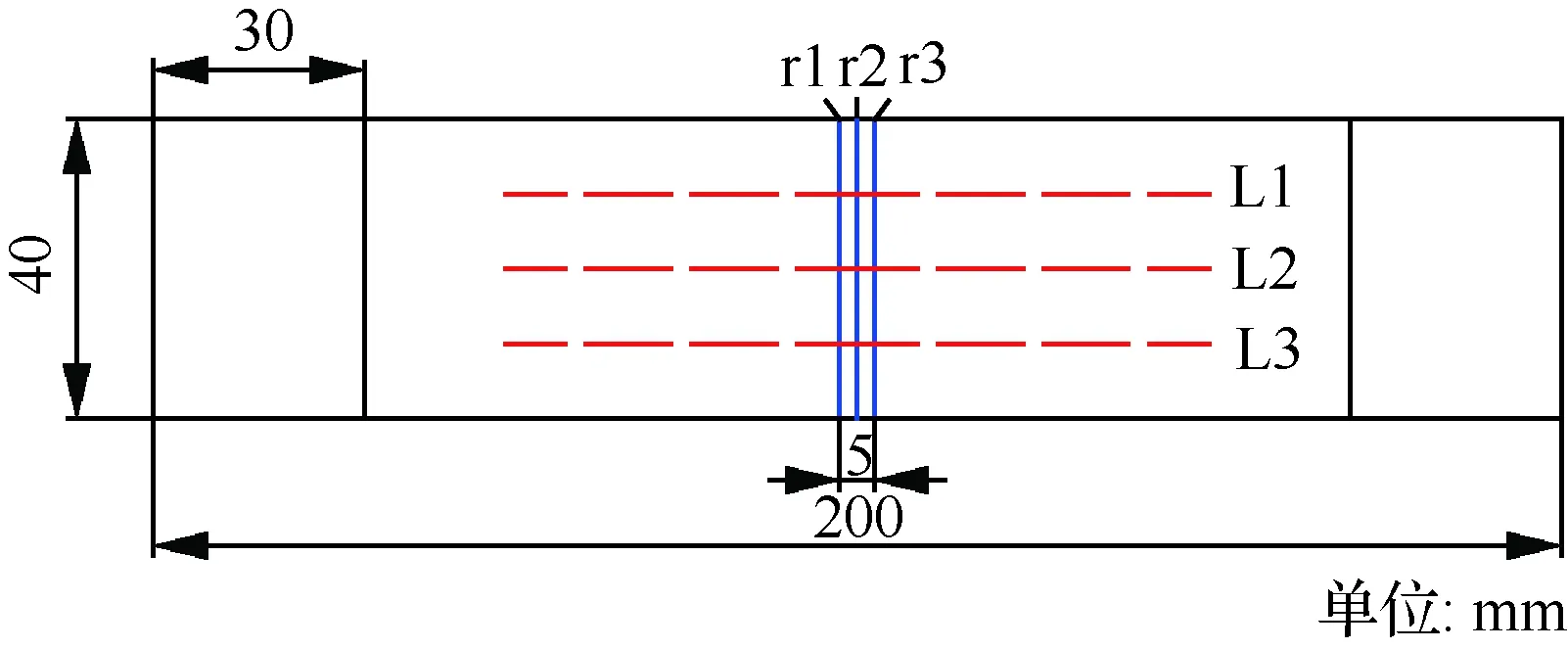
图1 试件结构尺寸Fig.1 Size of specimen structure

1.2 射线检测

对含有不同缺陷的焊接试件进行射线检测，采用XY-2515射线机和CR射线扫描仪，设置电压为130 kV，电流为5 mA，曝光时间为500 ms。射线检测结果如图2所示。可以看出，未焊透缺陷均贯穿整条焊缝，夹渣缺陷亦在图中圈出。

图2 射线检测图片Fig.2 Picture of ray detection

1.3 试验测量方法

如图1所示，分别在垂直焊缝方向(横向测量—X轴)和沿焊缝方向(纵向测量—Y轴)的3条测量路径上取采样点。在垂直焊缝方向的每条测量路径上，共采样25个点，每个采样点间距2 mm，其中在焊缝上的5个采样点间距为1 mm，总测量路径45 mm；在沿焊缝方向的每条测量路径上，共采样11个点且每个采样点间距2 mm，总测量路径20 mm。

根据所选材料的屈服强度和抗拉强度，在8801伺服疲劳试验机上对夹渣3#焊板进行疲劳试验。通过对15个含夹渣焊件进行屈服和抗拉强度的测定，可知其抗拉强度均值为237 MPa。故根据材料的力学性能，设定应力比为0.1，频率为20 Hz，动载为9.9 kN，静载为8.1 kN；每循环到一定周次时，将试件卸下且同一南北方向置于远离铁磁性物体的试验台上，并用LakeShore 421型弱磁场检测仪的切向探头和法向探头分别沿焊缝的横向测量路径L1、L2、L3和纵向测量路径r1、r2、r3进行磁感应强度法向分量B(y)和切向分量B(x)的测量。随后将试件重新置于疲劳测试机上，重复以上操作，直到试件断裂。

2 试验结果与讨论

2.1 含夹渣缺陷焊板的磁记忆信号特征

1) 不同疲劳循环次数的磁记忆曲线

在该疲劳试验中，测试次数与疲劳循环次数N的对应关系如表1所示。通过对不同疲劳循环次数下磁场值的分析处理，得出不同测量方向不同路径下的磁记忆切向分量和法向分量的疲劳曲线分别如图3～图6所示。在图3和图4的横向测量疲劳曲线中出现磁记忆检测的传统判据特征，即磁场法向分量B(y)过零点，切向分量B(x)具有最大值，且在疲劳载荷的作用下，特征值表现的更为明显。但是在图5和图6中未出现磁记忆传统判据特征，且无法从图5～图6中看出磁记忆信号随疲劳循环次数的变化规律以及对此含夹渣缺陷构件的疲劳寿命进行预测，因此须进一步提取磁记忆信号特征。

表1测试次数与疲劳循环次数的对应关系

Table1Relationshipbetweentesttimesandfatiguecycletimes

测试次数疲劳循环次数测试次数疲劳循环次数10.25×10472.50×10420.50×10483.50×10430.75×10494.50×10441.00×104106.00×10451.25×104118.00×10461.50×1041212.0×104

图3 不同疲劳损伤状态下焊缝横向测量磁记忆信号法向分量的分布特征Fig.3 Distribution characteristics of normal components of magnetic memory signals in transverse fatigue measurement under different fatigue damage conditions

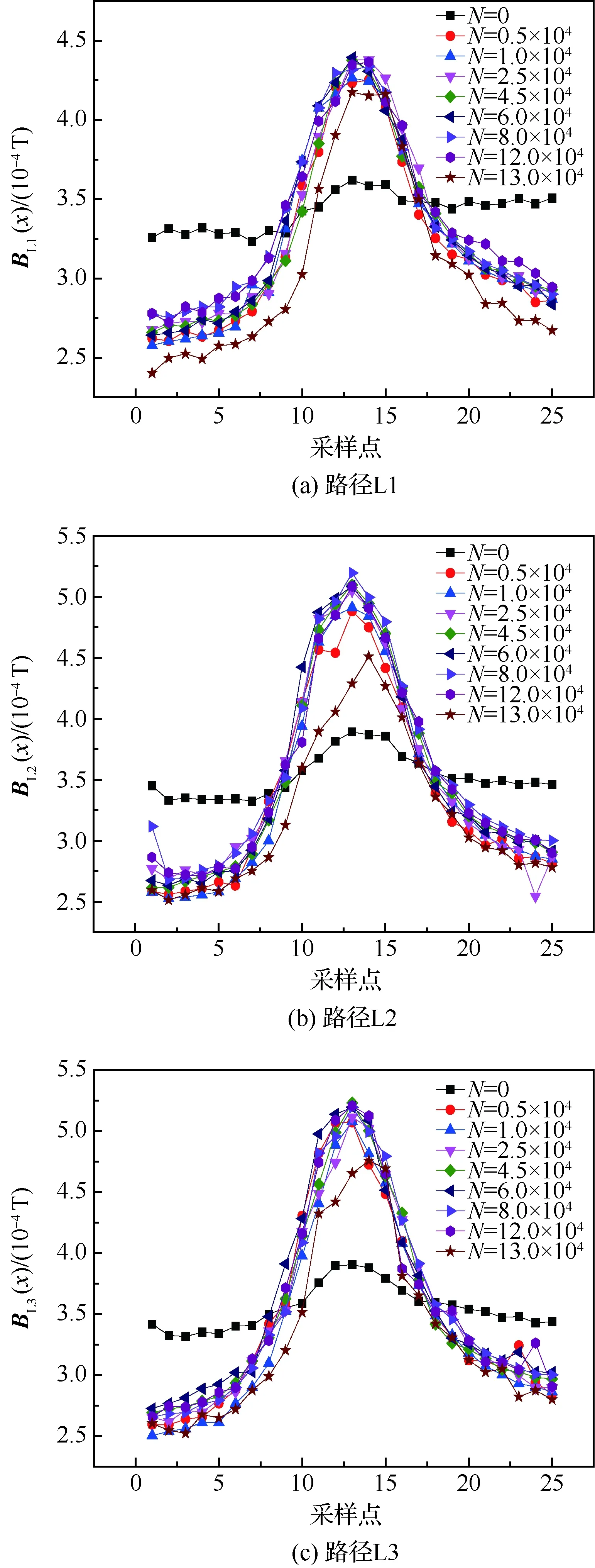
图4 不同疲劳损伤状态下焊缝横向测量磁记忆信号切向分量的分布特征Fig.4 Distribution characteristics of tangential components of magnetic memory signals in transverse measurement of weld fatigue under different fatigue damage conditions

图5 不同疲劳损伤状态下焊缝纵向测量磁记忆信号法向分量的分布特征Fig.5 Distribution characteristics of normal components of magnetic memory signals in longitudinal measurement of welds under different fatigue damage conditions

图6 不同疲劳损伤状态下焊缝纵向测量磁记忆信号切向分量的分布特征Fig.6 Distribution characteristics of tangential components of magnetic memory signals in longitudinal weld measurement under different fatigue damage conditions

2) 不同疲劳循环次数磁记忆信号特征提取

根据图3～图6中横向测量下的磁记忆疲劳曲线，在图3的横向测量下的磁记忆法向分量疲劳曲线中，在焊缝区(采样点11～15)出现“正弦波”式波峰波谷的跳变，现对焊缝区内的采样点进行曲线拟合求出不同疲劳循环次数下的拟合斜率KL，并提取焊缝区波峰波谷处的不同循环次数下的差值(磁化状态变化量)DL；在图4的横向测量下的磁记忆切向分量疲劳曲线中，在焊缝区出现明显极值点，故提取焊缝处不同疲劳循环次数下的极值点ML，进而得出不同路径下的法向斜率KL、波峰波谷处的差值(磁化状态变化量)DL和切向峰值点ML随疲劳循环次数的变化曲线如图7所示；从图6中纵向测量下的磁记忆疲劳曲线可看出，不同路径的切向分量在不同疲劳循环次数下表现出的规律并不明显，需进一步提取切向分量在不同疲劳循环次数下每条路径的磁记忆曲线的拟合斜率kr(x)，那么相对应的不同路径下的纵向测量的拟合斜率曲线如图8所示。

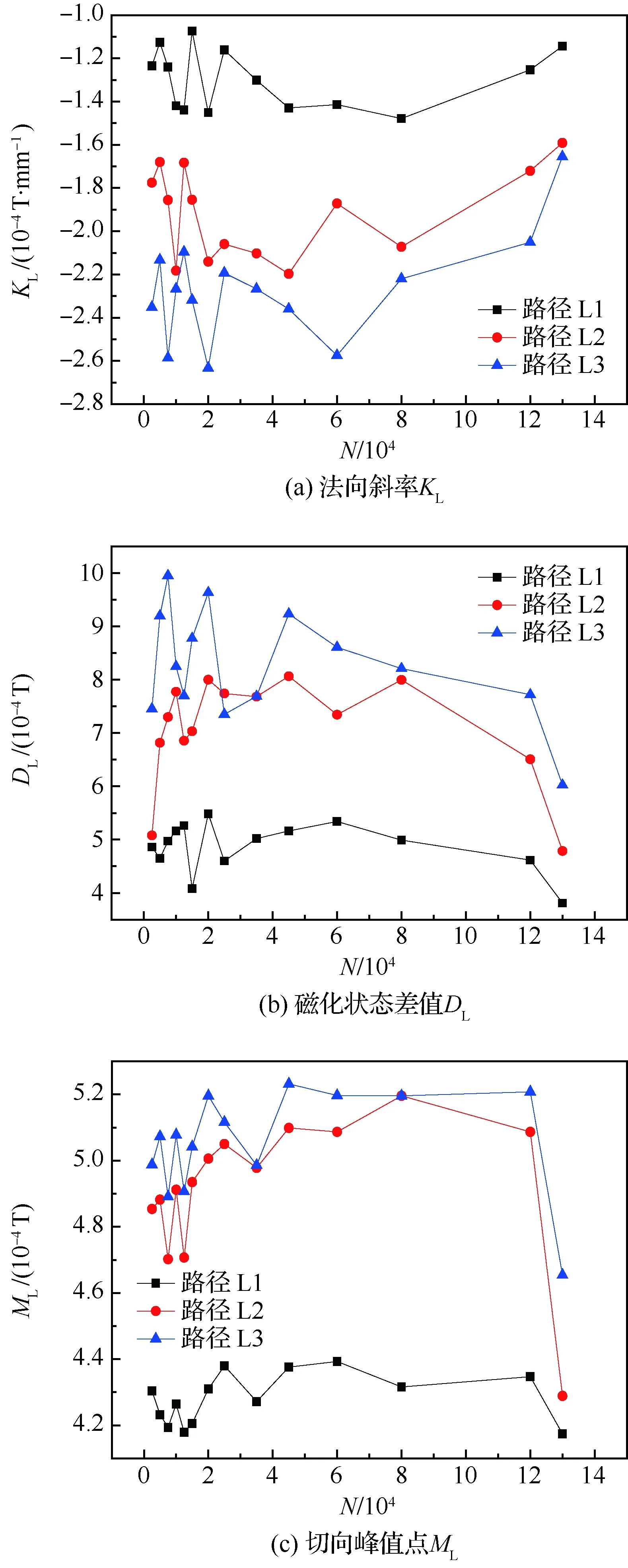
图7 横向测量路径下磁特征随疲劳次数的变化曲线Fig.7 Curves of magnetic characteristics with fatigue times under transverse measurement path

从图7中可看出，在疲劳应力循环初期，磁特征值的变化势趋均不明显，在疲劳循环次数达到8×104次后，法向分量的拟合斜率KL逐渐增大，但磁化状态变化量DL逐渐减小，而切向分量的峰值点ML却依然趋于稳定，直到疲劳达到12万次后，切向分量的峰值点ML迅速降低，直至焊件断裂；而从图8中可看到，在疲劳循环次数达到12万 次后，切向分量的拟合斜率kr(x)迅速增大。由此可知，横向测量路径下的法向分量的拟合斜率KL、磁化状态变化量DL、切向分量的峰值点ML和纵向测量路径下切向分量的拟合斜率kr(x)均不能很好地表征焊缝试件在疲劳循环载荷作用下的变化特征，会受到检测方向等因素的影响，所得出的结论也存在着很大的偶然性。为了消除这些影响，这里引入磁场矢量分析法来进行疲劳损伤模型的建立与评估。

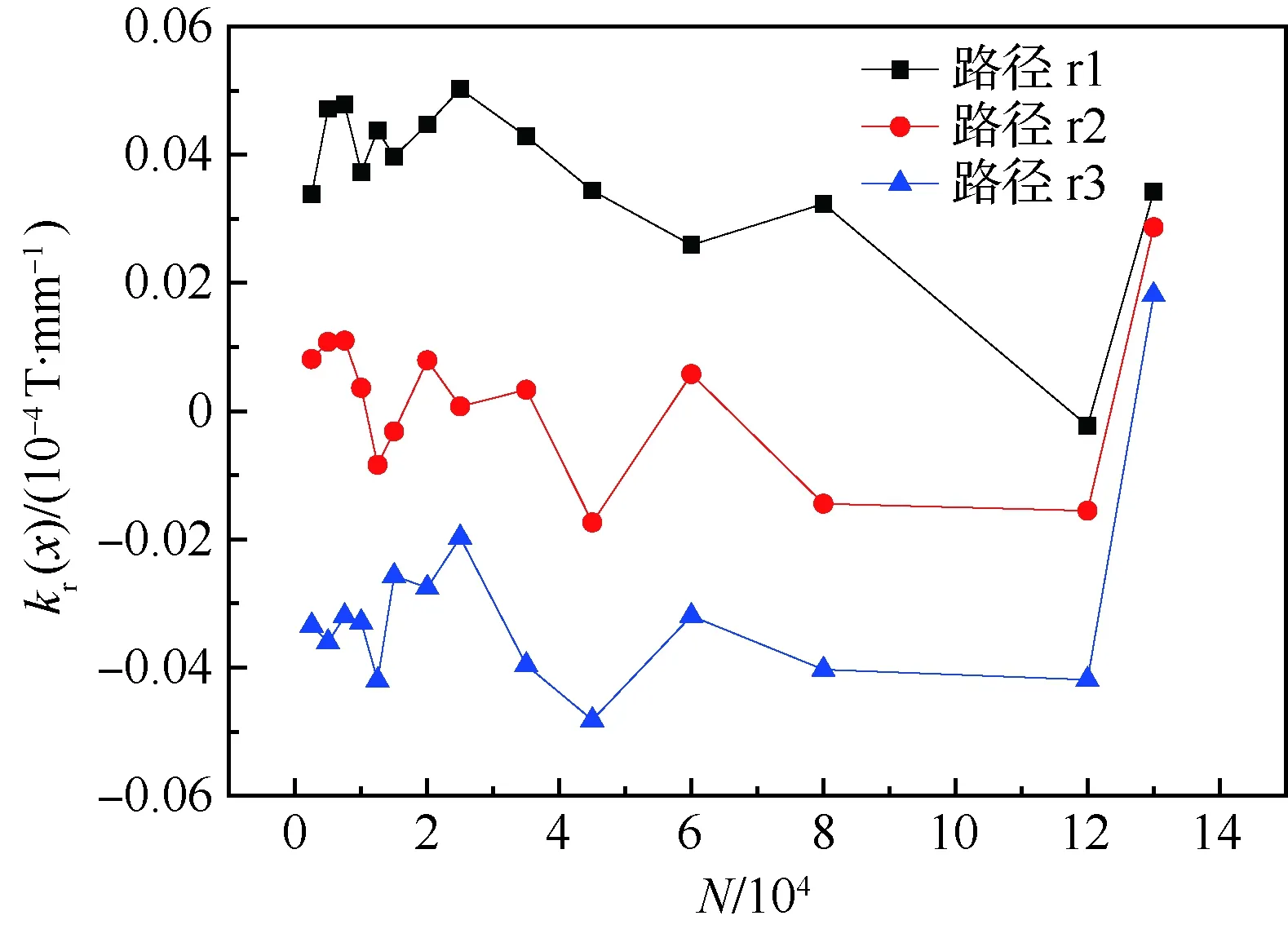
图8 纵向测量路径下切向斜率随疲劳次数的变化曲线Fig.8 Curves of tangential slope with fatigue times under longitudinal measurement path

2.2 基于磁场矢量特征的疲劳损伤模型

李萨如图是两个频率在两个互相垂直的方向做简谐运动时所形成的闭合曲线，它可以同时反映磁场法向和切向两个方向上的信息，防止了数据测量时偶然性的产生以及磁信号特征的丢失。任吉林等[17-18]根据二维检测原理，在磁记忆检测技术中率先引入李萨如图分析法，用法向和切向两个方向的分量微分后合成的李萨如图的区域面积来判断构件的应力集中程度，进而促进了磁记忆在二维定量检测上的研究。本文在李萨如图分析法的基础上，以磁场梯度特征为基数，提出磁场矢量梯度积分特征以及磁场矢量合成梯度特征来对损伤焊缝构件的状态进行评价，并建立疲劳累积损伤模型。

1) 磁场梯度积分特征

在磁记忆检测技术中，磁场梯度值是非常重要的一个参数，磁场矢量梯度积分就是在磁场梯度的基础上对曲线进行积分得出的，所用公式为

(1)

(2)

式中：ky和kx分别表示磁场法向梯度和磁场切向梯度；S(ky)和S(kx)分别表示磁场法向梯度积分和磁场切向梯度积分。

现分别求出不同检测方向下各自3条路径的磁场梯度积分的平均值,分别如图9和图10所示。可以看出，不同检测方向下的法向磁场梯度积分和切向磁场梯度积分所呈现的规律大体一致，在疲劳载荷循环的初始阶段，即在疲劳循环次数小于4.5×104次时，磁场梯度积分均在小范围内波动；但是当疲劳循环次数大于4.5×104次时，磁场梯度积分逐渐降低，在疲劳循环次数为8×104次时，出现拐点，此后磁场梯度积分迅速增大，直至焊件断裂。因此通过大量数据进行验证，不同检测方向下的法向和切向磁场梯度积分可以作为焊件的疲劳损伤判据之一。

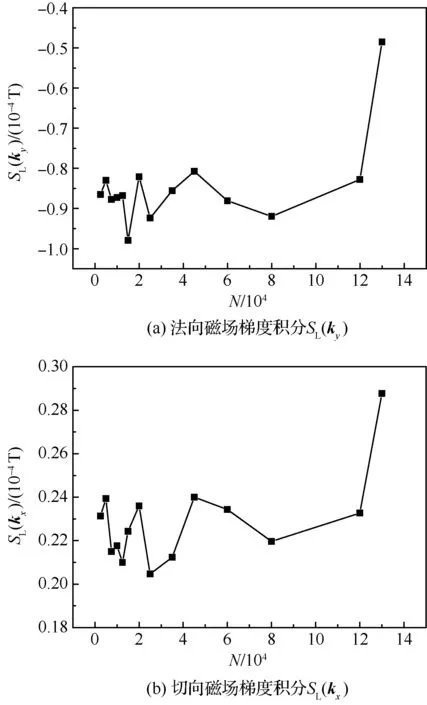
图9 横向测量下的磁场梯度平均积分特征曲线Fig.9 Characteristic curves of magnetic field gradient average integral under transverse measurement

图10 纵向测量下的磁场梯度平均积分特征曲线Fig.10 Characteristic curves of magnetic field gradient average integral under longitudinal measurement

2) 磁场矢量合成梯度特征

焊件焊接过程中，会受到焊件初始状态和材料性能等因素的影响。用磁记忆检测方法对焊件进行疲劳损伤评估时，采用磁场值B(x)和B(y)、磁场强度Hp(x) 和Hp(y)、磁场梯度ky和kx等单一特征量展开研究时都存在一定的偶然性，因此本文采用磁场矢量合成梯度特征G来进行建模研究，以消除这些影响。现对不同方向检测路径的切向梯度值和法向梯度值采取矢量运算，即

(3)

(4)

式中：GLmax为横向测量下磁场矢量合成梯度的最大值；Gravg为纵向测量下磁场矢量合成梯度的平均值；klx和kly为横向测量下的切向磁场梯度和法向磁场梯度。

现求出在疲劳循环载荷作用下该焊件的磁场矢量合成梯度的最大值GLmax和平均值Gravg分别如图11和图12所示。从图中可以看出，与磁场梯度积分特征所呈现的规律相似，在疲劳循环的初始阶段的磁场矢量合成梯度值波动范围小，在疲劳循环次数达到4.5×104次时GLmax和Gravg达到最大；随后进入疲劳循环的扩展阶段，特征值GLmax和Gravg逐渐降低，并在疲劳循环次数8×104时形成拐点；此后疲劳循环进入到失稳阶段，特征值GLmax和Gravg开始迅速增大，直至试件断裂。那么为了更进一步简单明了的描述该焊件的疲劳损伤过程，现将横向测量和纵向测量3条路径下的磁特征(GLmax和Gravg)变化曲线分别平均合成，所得曲线如图13所示。因此不同检测方向下的磁场矢量合成梯度的峰值和均值可以作为评价焊件疲劳损伤程度的特征量。

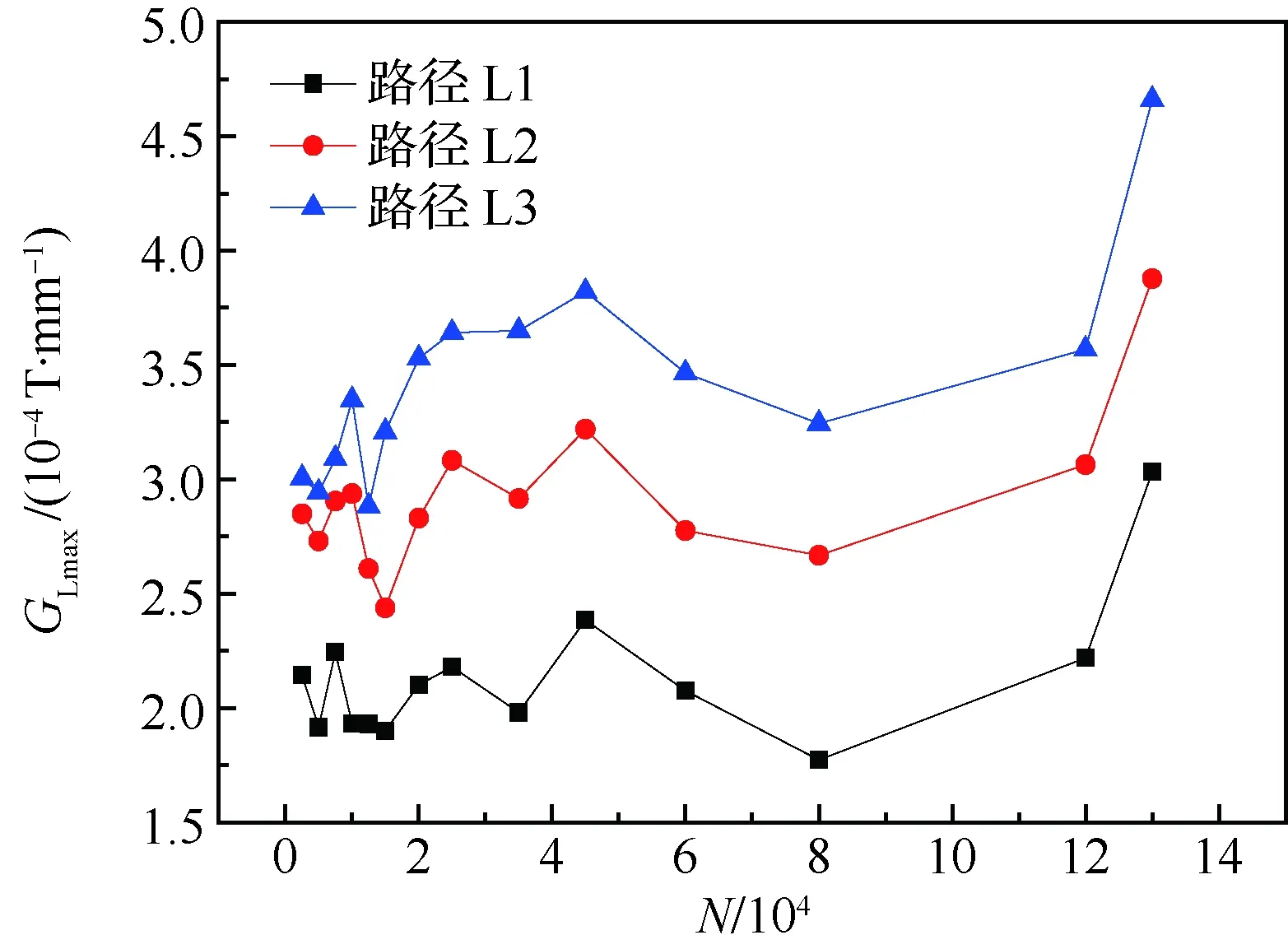
图11 横向测量下不同路径的磁场矢量合成梯度峰值GLmax随疲劳次数的变化曲线Fig.11 Curves of magnetic field vector synthesis gradient peak GLmax with fatigue times of different paths under lateral measurement

图12 纵向测量下不同路径的磁场矢量合成梯度均值Gravg随疲劳次数的变化曲线Fig.12 Curves of magnetic field vector synthesis gradient mean value Gravg with fatigue times of different paths under longitudinal measurement

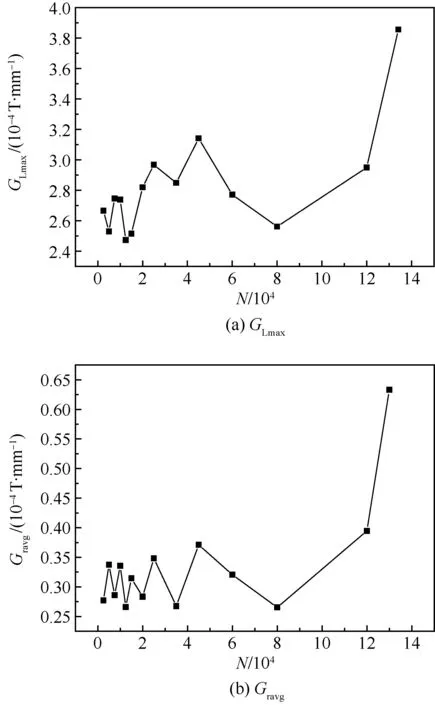
图13 横向和纵向测量3条路径下磁场矢量合成梯度特征值随疲劳次数的变化曲线Fig.13 Curves of eigenvalue of magnetic field vector synthesis gradient under lateral and longitudinal of three path with fatigue times

2.3 焊缝疲劳损伤模型的评估与分析

根据Miner疲劳损伤理论[19-20]，当试件在相同幅值的恒定应力作用下，定义试件的整体寿命为N，那么在承受n次循环应力时的损伤为：D=n/N，其中D表示损伤参量。那么若n=0，则D=0，材料没有发生疲劳损伤破坏；若n=N，则D=1，材料发生疲劳破坏即完全失效。

假定对试件施加一个应力σi，并循环ni次失效，则损伤参量为Di=ni/Ni，若对试件施加k个应力σi(i=1,2,…,k)，并各自循环ni次，那么可将受到的总损伤参量定义为

(5)

定义材料发生完全损伤准则[21-22]为

(6)

为了进一步对含隐形损伤焊接构件的疲劳损伤进行定量研究与评价，现分别以磁场矢量合成梯度特征值GLmax和Gravg为损伤参量D，建立损伤参量D与疲劳剩余寿命Nr之间的关系，利用指数关系拟合函数对其进行非线性拟合，得到特征值GLmax和Gravg与疲劳剩余寿命Nr之间的量化公式为

D1=GLxmax=A1e-Nr/t1+K1

(7)

D2=Gravg=A2e-Nr/t2+K2

(8)

那么根据图13所示的正交矢量合成梯度特征值随疲劳循环次数的变化曲线，将其转化为与剩余疲劳寿命Nr的特征曲线，利用MATLAB软件对特征参量GLmax和Gravg进行指数函数的非线性拟合，并用origin软件作图，如图14所示。

对于焊缝横向检测来说，A1=1.13，t1= 0.065 73，K1=2.732；对于焊缝纵向检测来说，A2= 0.327 5，t2=0.081 4，K2=0.306 1。

图14 疲劳剩余寿命Nr与特征参量GLmax和Gravg的拟合曲线Fig.14 Fitting curves of fatigue residual life Nr and characteristic parameters GLmax and Gravg

2.4 焊缝疲劳损伤模型的理论分析与试验验证

1) 焊缝疲劳损伤理论分析

焊接构件在疲劳过程中，受到连续循环的应力作用，材料内部晶粒之间就会不断的发生变形与压缩，焊接接头的内部缺陷损伤就会逐渐演变、扩展和延伸，直至试件的断裂。根据位错原理和能量理论，在疲劳裂纹扩展的初始阶段，在疲劳循环应力作用下焊接接头内部会出现疲劳硬化，焊接缺陷处内部应力能增大，出现小范围屈服现象，表现出焊缝表面的磁场值特征出现小范围的波动现象；在疲劳裂纹的稳定扩展阶段，焊缝内部焊接缺陷尖端处位错不断增加，裂纹继续向外延伸，内部点阵之间的阻力与位错相互作用形成位错塞积群，会阻碍磁畴的形成，从而造成磁弹性能的减少；然而，位错塞积群也会造成在缺陷的裂纹尖端处应力能的增加。那么根据能量最小原理，这二者之间相互制衡。在含有焊接缺陷的“先天”裂纹源存在时，前者稍微占据优势，从而表现出磁场特征值GLmax和Gravg随疲劳循环次数N的增加有减小的趋势；在疲劳裂纹的失稳扩展阶段，在焊接缺陷的裂纹尖端，逐渐向四周扩展，出现大面积的屈服，从而产生非常大的位错塞积群，生长迅速且应力能急剧增多，而内部位错对磁畴的阻碍减小，即磁弹性能迅速增加，表现出磁记忆信号的特征值GLmax和Gravg随疲劳循环次数N的增加而迅速增大，直至焊件断裂。

2) 焊缝疲劳损伤模型验证

为了验证2.3节中所建立的疲劳剩余寿命Nr与特征参量GLmax和Gravg的关系模型的正确性，现用相同材质的另一组夹渣2#焊件和相同材质的含未焊透缺陷的焊件来进行相关验证。首先是用另一组含夹渣缺陷的试件进行验证，重复上述试验过程并进行数据的采集与分析，得出特征值GLmax和Gravg与疲劳剩余寿命Nr的拟合曲线如图15 所示。

其次，用含有未焊透缺陷的试件进行模型验证。与含夹渣缺陷焊接件的分析方法相同，通过对未焊透3#试件的疲劳曲线分析和不同检测方向的磁记忆疲劳曲线的法向斜率kL/r(y)和切向斜率kL/r(x)、法向和切向磁场梯度以及磁场梯度积分和磁场矢量合成梯度等特征量的提取与分析，得出不同检测方向下不同路径的磁场矢量合成梯度特征值GLmax和Gravg的平均值随疲劳循环次数的变化曲线如图16所示。可知，在疲劳初期，特征值GLmax和Gravg随着疲劳循环次数的增大缓慢降低，在1万次时出现“拐点”，此后特征值GLmax和Gravg迅速上升，直至试件断裂。因此不同检测方向下的磁场矢量合成梯度的峰值和均值可以作为评价焊件疲劳损伤程度的特征量。

图15 夹渣2#试件疲劳剩余寿命Nr与特征参量GLmax和Gravg的拟合曲线Fig.15 Fitting curves of fatigue residual life Nr and characteristic parameters GLmax and Gravg of 2# specimen

同理，以磁场矢量合成梯度特征值GLmax和Gravg为损伤参量D，建立损伤参量D与疲劳剩余寿命Nr之间的关系，如图17所示。

图16 未焊透3#试件磁场矢量合成梯度特征值随疲劳循环次数的变化曲线Fig.16 Curves of eigenvalue of magnetic field vector synthesis gradient with fatigue cycle times of 3# specimen

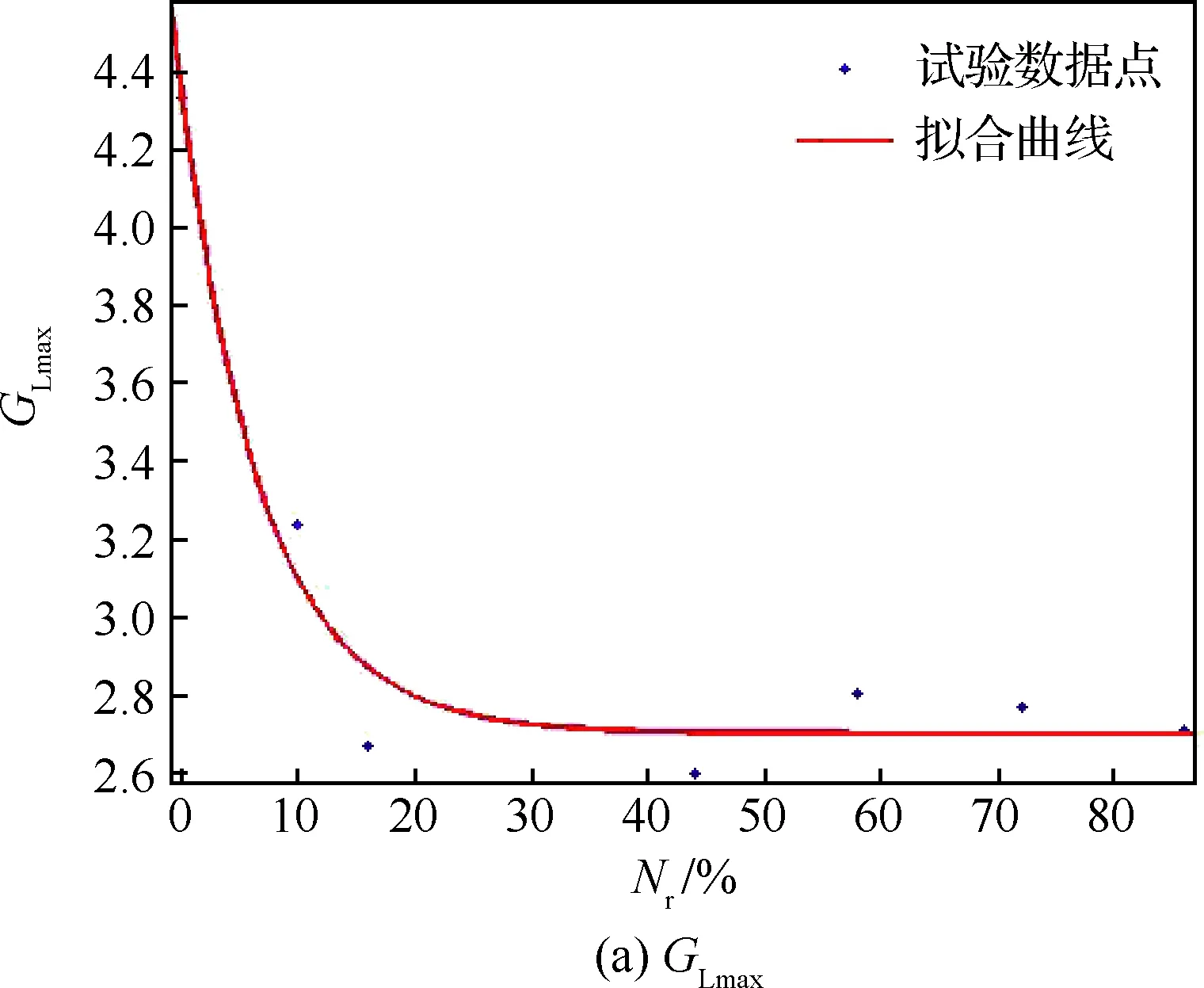
图17 未焊透3#试件疲劳剩余寿命Nr与特征参量GLmax和Gravg的拟合曲线Fig.17 Fitting curves of fatigue residual life Nr and characteristic parameters GLmax and Gravg of 3# specimen

在图17中，对于焊缝横向检测来说，A1=1.648，t1=0.070 23，K1=2.702；对于焊缝纵向检测来说，A2= 0.344 3，t2=0.072 12，K2=0.239 5。

3 结 论

1) 通过对含有夹渣和未焊透缺陷焊件的疲劳累积损伤的试验研究与不同测量方向下磁记忆法向分量和切向分量的测量，得出在横向测量线上，磁信号曲线具有磁记忆检测的传统判据特征：法向磁场分量过零点和切向磁场分量具有最大值，但在纵向测量下的磁信号曲线中并未体现。

2) 通过对含有夹渣缺陷焊件的疲劳累积损伤曲线分析与磁特征值的提取，得出单一测量方式下的磁特征值并不能很好地表征焊件在疲劳循环载荷下的变化特征，会受到检测方向等因素影响，所得结论存在偶然性。

3) 根据李萨如图分析法，以磁场梯度特征为基础，提出磁场矢量特征分析法，通过提取磁场矢量梯度积分特征S(ky)、S(kx)和磁场矢量合成梯度特征G对焊接试件的疲劳损伤过程进行分析。可知磁信号特征值S(ky)、S(kx)和G随着疲劳循环次数的增加，均表现出了疲劳3个阶段的变化特征，随着应力集中和疲劳损伤程度的加剧而逐渐增大，且消除了检测方向不同等因素所带来的偶然性。

4) 以磁场矢量合成梯度特征的最大值GLmax和平均值Gravg为损伤参量，通过指数函数进行非线性拟合，建立了特征参量GLmax和Gravg与疲劳剩余寿命Nr的损伤关系模型，进而可对含有隐形损伤焊接件的疲劳寿命进行定量评估，为磁记忆技术在焊接缺陷定量评价上的研究提供一种新思路。