例谈比 较数或式大小的方法
2019-03-28眭亚燕
眭亚燕

我们在分析、解决某些数学问题时,经常要比较两个实数或代数式的大小,在实际操作时,需要根据实数或代数式的特点来选择适当的方法进行比较,才能方便快捷地获得准确的结果。
一、法则法
比较实数大小的法则有:①在数轴上表示的两个数,右边的数总比左边的数大;②正数都大于0,负数都小于0,正数大于负数;③两个正数比较大小,绝对值大的正数大;④两个负数比较大小,绝对值大的负数小。这些方法常用于比较有理数的大小。
例1实数a,b,c,d在数轴上对应的点的位置如图所示,这4个数中最大的是( )。

A.a B.b C.c D.d
【解析】由数轴可知,a<b<c<d,故选D。
二、平方法
对任意正实数 a、b,若 a2>b2,则 a>b;对任意负实数a、b,若a2>b2,则a<b。这种方法常用于比较无理数的大小。
例2比较大小:(1)23;(2)
【解析】(1)首先分别求出2、3的平方,然后判断出2、3的平方的大小关系,即可判断出2、3的大小关系。易得2>3。


三、估算法
对任意正实数a、b,先估算出a、b两数或两数中某部分的取值范围,再进行比较。这种方法常用于比较无理数的大小。
例3若a=,b=,则实数a、b的大小关系为( )。
A.a>b B.a<b C.a=b D.a≥b
【解析】解决此题的关键是正确估算出、中被开方数26和11分别在哪两个相邻整数的立方、平方之间。

四、赋值法
赋值法也称特殊值法,即在解决含有字母的选择题或填空题时,常常可以在字母给定的范围内取特殊值,从而比较快地得出答案。
例4已知-1<b<0,0<a<1,则代数式a-b、a+b、a+b2、a2+b中值最大的是_______。
【解析】根据条件,不妨设b=-0.5,a=0.5,则a-b=1,a+b=0,a+b2=0.75,a2+b=-0.25。故ab的值最大。
五、求差法
对任意实数a、b,若a-b>0,则a>b;若ab=0,则 a=b;若 a-b<0,则 a<b。反之也成立。这种方法常用于比较两个较复杂的无理数或分式的大小。
例5已知a、b、c分别是△ABC的3条边长,试比较分式的大小。


∵a、b、c分别是△ABC的3条边长,
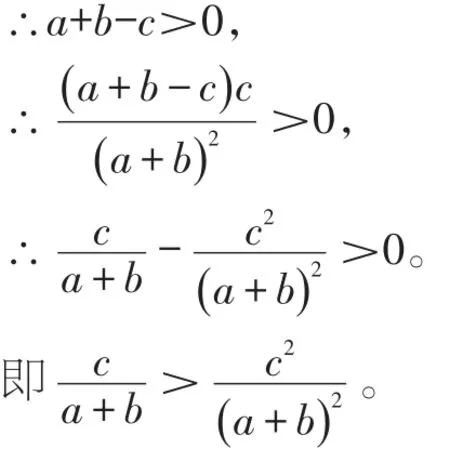
六、求商法
例6比较218×310与210×315的大小。
【解析】本题若先计算出结果,再进行比较,相当困难。观察可发现,它们有相同底数的因数,我们采用求商法解决此题。
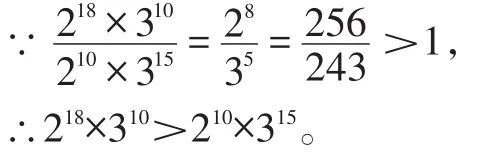
七、倒数法
设a、b为任意两个正实数,先分别求出a与b的倒数,再根据“当时,a<b”来比较a与b的大小。
例7比较的大小。
【解析】当几个式子中的被开方数的差相等,如2017-2016=2018-2017,且式子中的运算符号相同(都是减号)时,可选用倒数法。


八、放缩法
如果a<c,c<b,那么a<b。若通过放缩能够确定两个实数中的一个数比某个数小,而另一个数恰好比该数大时,可选用此法。
例8比较245与511的大小。
【解析】注意到前者的底数24接近52,采用放缩法,可知 245<255=(52)5=510<511,所以245<511。
九、参数法
例8 比较下面两个数的大小:

【解析】题目中是比较两个根式之间的大小,因为根号内均为正整数,所以只要比较根号内两式大小即可。
设参数x=54322,则54321=x-1,54323=x+1,54324=x+2,则只需比较(x-1)(x+2)与x(x+1)的大小即可。

十、穿越法
穿越法亦称移动因式法。当a>0,b>0,若要比较形如a b与c d的大小时,可先把根号外的因数a与c平方后,移入根号内,再根据被开方数的大小进行比较。
例10比较大小:4____5。(填“<”“=”“>”)
【解析】因为两数均为正无理数,所以把它们化为二次根式的形式,然后比较被开方数的大小即可解决问题。

十一、相“同”法
已知a、b、c都为正整数,对于同指数且不同底数的两个幂 ab与 cb,当 a>c时,ab>cb;对于同底数且不同指数的两个幂ab与ac,当b>c时,ab>ac。
例11(1)比较大小:210310。
(2)试比较722与266的大小。
【解析】(1)根据同指数的“幂底数越大幂越大”,可得答案为210<310;(2)根据幂的乘方,可得指数相同的幂,根据底数越大幂越大,可得答案。
∵266=822,∵7<8,∴722<822,即722<266。
十二、规律法
例12 你能比较两个数20092010和20102009的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较nn+1和(n+1)n的大小(n为自然数),然后我们从简单情形入手,从中发现规律,经过归纳,猜想出结论。
(1)通过计算,比较下列各组数的大小:
①1221;②2332;③3443;
④4554;⑤5665…
(2)从(1)的结果归纳,可以猜想出nn+1__(n+1)n(n≥3)。
(3)根据上面归纳猜想得到的一般结论,试比较下列两个数的大小:
①2009201020102009。
②-20092010-20102009。
【解析】解决本题的关键是计算正确,并猜想得出nn+1>(n+1)n(n≥3),从而根据这个一般结论,得到①20092010>20102009;②-20092010<-20102009。
