棋室的小插曲
2019-03-28李晓芳
○李晓芳
学校的第二课堂小组活动开展得如火如荼,这学期报名参加棋类小组的同学热情空前高涨,人数多达120 人。瞧,上课铃一响,同学们三五成群快步来到棋室。两人一副象棋,六人一副跳棋,齐刷刷地坐到座位上开始了这周的大比拼。
此时,年轻的陈校长正好经过棋室,看到同学们兴致勃勃的劲头,和辅导教师李老师亲切地聊起天来。陈校长不经意地问道:“我看了一下,同学们主要在玩象棋和跳棋,棋具还充足吗?”李老师回应道:“这些棋具都是今年新购进的,一共是26副,非常好用。”陈校长点了点头又问:“是吗?象棋和跳棋各有多少副啊?”李老师不好意思地说:“我只关注了一下总数,还没有分类统计,等我收上来分别数一数。”陈校长笑着说道:“不急、不急,我只是随意问问。”这时,近处的文奇耳朵很尖,插嘴道:“你们的谈话我听到了,要想知道象棋和跳棋各有多少副,这个问题我们能解决。”
陈校长来到他跟前,摸着他的头说:“哦?你说说看。”这时,同学们都停下了手上的动作,一齐看向谈话的两人。文奇慢条斯理地说:“假设都是象棋。那么26副棋就有26×2=52 人,而实际有120 人,就差了120-52=68 人。这是因为26 副棋里还有跳棋,一副跳棋6个人,当象棋算时一副跳棋就少算了6-2=4人,那么少算了68 人,就说明有68÷4=17 副跳棋。所以,跳棋:(120-26×2)÷(6-2)=17副,象棋:26-17=9副。也可以假设都是跳棋从而求得。”
陈校长总结说:“同学们这题可以看作鸡兔同笼问题,假设法是解决这类问题的一般方法。”
李老师作为经验丰富的数学教师哪能放过这个机会,意味深长地说道:“既然是一般方法,就会有巧妙方法嘛!”
同学们你一言我一语议论开了,由于没带纸笔,便自由结组到黑板上用粉笔边画边算起来。
口齿伶俐的佳逸边指边说:“我们几个用了画线段图法来解答。(见下图)每条短线段表示一副象棋,它的长度代表2人(不管有多少,随意画出几条);每条长线段表示一副跳棋,它的长度代表6 人,同样随意画出几条。画竖向线段,它的左边每条线段都是2人,就是26×2=52人。竖向线段右边长线段有多少呢?120-52=68 人,每条长线段剩下的是4 人,用68÷4=17 副,就是跳棋数。象棋数是26-17=9副。

李老师赞赏地说:“数形结合形象直观地解决了这个问题,为你们点赞!”
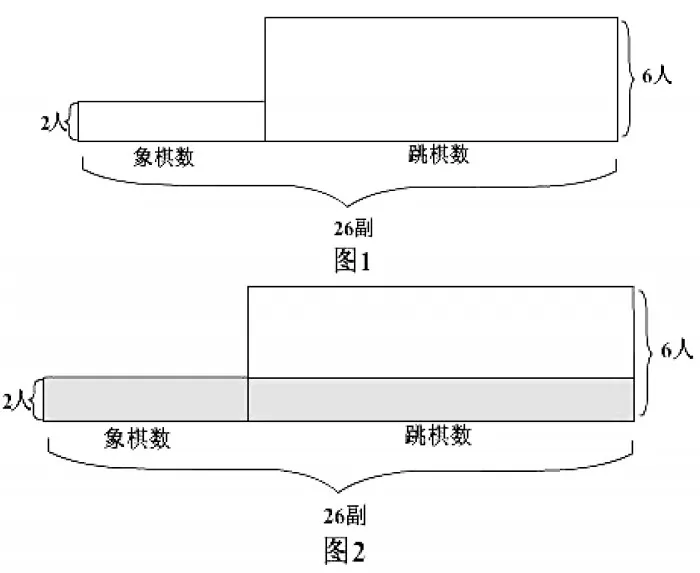
梓轩沉不住气了,高举小手说:“我们利用面积关系画矩形图来解答(见图1)。先画一个小长方形,长代表象棋数,宽代表一副象棋2 人,小长方形面积就是玩象棋总人数。再在右侧画一个大长方形,长代表跳棋数,宽代表一副跳棋6 人,大长方形面积就是玩跳棋总人数。从图1 可知,小长方形面积+大长方形面积=120 人。(见图2)把小长方形的上面长边延长相交于大长方形,得到阴影长方形,阴影长方形面积+空白部分面积=120人。阴影长方形的长就是象棋数+跳棋数=26 副,宽是2 人,阴影长方形面积是26×2=52 人,用120-52=68 人就是上面空白部分面积。上面空白部分面积宽是6-2=4人,上面空白面积长是68÷4=17副,也就是跳棋数,26-17=9副,就是象棋数。
陈校长热烈地鼓起掌来:“好了,棋室的小插曲到此为止,不再耽误同学们的第二课堂时间。正如数学家华罗庚所言:‘数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休。’同学们小小年纪就能打破常规,巧思妙解,很了不起!”
