交汇河道水动力特性和污染物掺混规律研究综述

，，，，，

(1.浅水湖泊综合治理与资源开发教育部重点实验室，江苏南京210098； 2.河海大学环境学院，江苏南京210098；3.句容市水利农机局，江苏句容212400)

天然河流中普遍存在着干支流交汇现象，干支流通过交汇口作为节点连接形成水系乃至河网，河网是地表水循环系统的重要组成部分，也是流域水流、泥沙等物质输移的重要通道。在河道交汇处，水流紊动掺混剧烈，并对泥沙、污染物输移有较强的滞留作用，成为水利、航运、环保部门关注的重点区域，也是学者研究的重点。自1944年Taylor首次对汇流口开展研究以来，交汇河道水动力特性研究至今已有70多年历史，研究内容已从水动力特性发展到泥沙、污染物输运规律及对水生态的影响，研究手段从室内物理模型试验为主发展到数学模型、物理模型、野外观测等多种手段相结合，取得了较为丰富的研究成果。本文对交汇口水动力特性和污染物输移规律研究进展进行综述，对尚需研究的问题提出了看法, 以期有助于推动中国交汇河道水动力特性和污染物掺混规律研究的进一步发展。

1 河道交汇的分类

天然河流中交汇形式多样，Best[1]于1988年首次将交汇口区分为支流斜接干流型交汇口与“Y”型交汇口。兰波[2]于1998年将交汇口分为“非对称型”和“Y”型2类，并统计分析认为山区河流中这2类交汇口数量基本相等。2010年张强认为传统分类未考虑到实际河型，不能反映出山区河流交汇口的真实特征，因此对传统的交汇口交汇形式进行研究将其重新划分为3类，即弯曲干流型交汇口、顺直干流型交汇口和分汊干流交汇口。本文采用的河道交汇分类体系见图1。

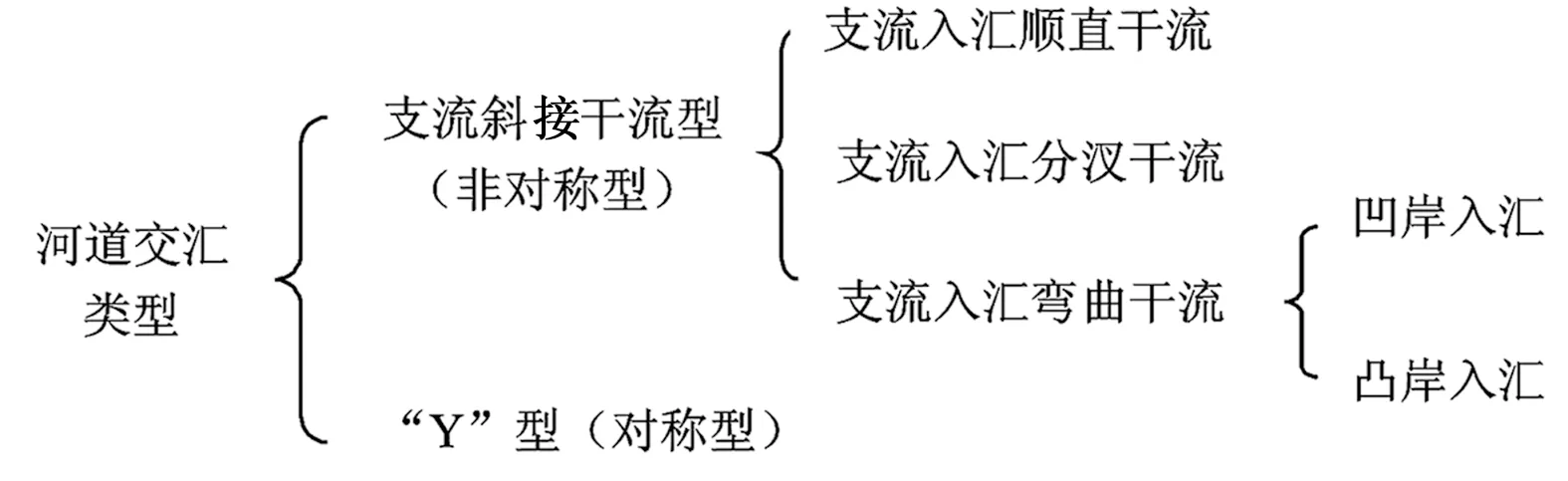
图1 河道交汇分类

2 河道交汇水动力特性的研究现状

2.1 原型观测和模型试验方面

在交汇河道水动力特性研究方面，国外开展的比国内要早，早期研究以物理模型试验为主，辅以野外原型观测。

2.1.1支流斜接干流型交汇

Taylor[3]最先通过模型试验，研究了等宽明渠交汇水流在不同交汇比下的水力特性，并给出了汇流比和交汇前后断面水深比的关系式。1984年Best[4]通过对交汇角为15°、45°、70°、90°的矩形水槽进行试验，研究了明渠交汇中分离区的大小，发现各交汇角工况下分离区的形状基本相似，但尺寸与交汇角成正比。之后，Best[5]继续对交汇河流的水流结构进行研究，给出了交汇水流的概化模型，并进行了水流分区，将交汇水流分出了6个区域：停滞区、流速偏向区、流速分离区、最大流速区、剪切层区及流速恢复区，见图2[5]。其后，Best[1]对交汇河道的水面形态和交汇区的沉积物输运等问题进行了深入探讨，发现这些问题与交汇水流的汇流比和交汇角息息相关。Best[6]还研究了河床高差对水流的影响，发现存在河床高差的交汇水流会存在剪切层变形，致使相应部位的水面凸起。之后，Biron和Best[7]等人根据概化的物理模型试验，继续研究干流的河床高程与支流的河床高程不一致时对水流构造的影响，观察到存在高程差时，交汇口处水流紊动强度被加强，高程不一致的部位分离区消退，流速加速区减弱，水流掺混更迅速。

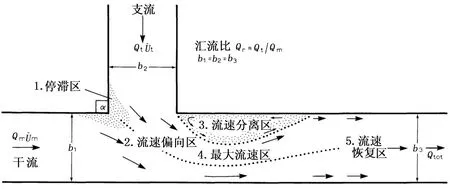
图2[5] 交汇河道的流动动力学

Hsu[8]等人通过研究90°的等宽交汇河道，给出了求解水流流动收缩区的动量及能量修正系数的计算方法和分离区形态系数与交汇角的理论关系式。同年Hsu[9]等人还研究了交汇角为30°、45°、60°的交汇河道，发现交汇前后水深比Hr与交汇角和弗劳德数Fr成正比，并给出了相应的关系公式。

Weber[10]等人对交汇口水流进行了三维性概化，利用ADV对直角明渠汇流处的三维水流结构进行测定，分析了水流流场分布和紊流结构以及水面变化等规律。Mignot[11]对交汇明渠中的混合层进行研究，发现等宽明渠交汇的混合层是加速并且弯曲的，并且通过雷诺时均法也表明，混合层的流向和法向加速度以及压力梯度保持主导地位，是典型的加速和旋转流。Biswal[12]对直角交汇明渠水流进行物理模型试验，探讨在一个硬床上的时间平均流结构的汇合，发现二次流和湍流应力随着汇流比的减小而加强，交汇处出现表面高程的凹陷区。

国内较早的相关研究是罗保平[13]在交汇口上游1 m的位置，利用铝片挂红线、投放固体高锰酸钾、投放红墨水以及分配流量这4种不同的方法来模拟研究干支流交汇处的掺混带及形态，并定义为干支流分界线。同期，周华君[14]收集长江嘉陵江交汇口的实测资料，结合物理模型试验，对交汇河道进行水力特性分析，发现汇流比对其影响很大。之后，兰波和汪勇[15]对四川省境内所有通航河道中的交汇河道进行了资料的收集与整理，分析发现这些交汇河道的交汇角几乎在30°～90°之间，并且交汇口的形态多为支流斜接干流型，所以据此开展了交汇角为30°、60°、90°的支流斜接干流型交汇河道的物理模型试验，发现交汇水流的水力特性受交汇角和汇流比的影响很大。

随着测量技术的发展，学者们开始使用各种先进的测量技术和方法对交汇河道进行研究。茅泽育[16]等应用数字粒子测速技术(DPIV)对不同汇流比下的交汇河道进行探究，发现交汇口附近存在流速分离区，其尺寸与汇流比有关，但形状基本相似，并表明数字粒子测速技术可高效直观地用于水力特性研究。其后，茅泽育[17]等应用五孔毕托球对45°等宽交汇的矩形水槽进行三维水力特性研究，发现与之前一样的结果，还发现交汇口处存在指向干流一侧的横向流速，下游断面中存在二次环流。在前期的基础上，茅泽育[18]等使用理论分析与模型试验相结合的手段，重点探讨不同交汇角和汇流比对水流分离区的影响，表明分离区的尺寸与汇流比和交汇角均有较好的相关性，并给出了相应的理论表达式。

王协康[19]等建立30°交汇的水槽模型，利用声学多普勒流速仪(ADV)测量三维流速进行分析，观察到交汇口处出现壅水现象和低流速区，交汇口附近出现有小范围的回流现象和分离区，下游出现方向各异的二次环流。

刘同宦[20]等也对交汇角为30°的交汇水流进行了研究，同样发现交汇口附近靠主流侧出现回流现象和分离区，向下游有环流结构，还发现靠近交汇口的水体其雷诺应力和脉动强度较远离交汇口的水体大。之后，刘同宦[21]等研究了不同汇流比下交汇角为90°的交汇水流，也表明交汇口附近有回流区和流速分离区，向下游存在交替的高流速带和低流速带，并表明交汇区的水面坡降随汇流比的减小而增大。

钟博刚[22]利用激光多普勒测速仪(LDV)分别对矩形断面和复式断面的不等宽水槽进行了试验研究，着重分析了交汇区的水力特性，得到与前人相似的研究结果，但并没有在复式断面的交汇口下游发现二次环流，还表明相同条件下，两者水力特性较类似，水头损失均随支流流量的增加而增大，但复式断面水槽的水流整体流场相对较稳定。海霞[23]在钟博刚直角交汇水槽试验的基础上，综合实际流域的水力特性，研究了汇流比和河床形态对交汇区水流结构的影响。得到水流结构会随河床形态变化而变化，但基本不受汇流比变化的影响，并进行了理论分析。

袁赛瑜[24]等通过水槽物理模型试验，探讨90°交汇明渠的水流流动特性和剪切层变形情况，根据试验对时均流速、湍流动能、雷诺剪切应力、湍流谱、象限事件的发生概率进行分析，发现最大的雷诺剪切应力主要分布在水流的中间区域，如果保持汇流比不变，加大交汇水流的流量，会导致水体流度、湍流动能和雷诺剪切应力的绝对值增加，但剪切层的扭曲程度随之减弱，并表明城市交汇明渠与天然交汇河流在泥沙输移、床面形态、污染物在剪切层中的传输会有显著的不同。

2.1.2“Y”型交汇

郭维东[25]等建立90°“Y”型交汇水槽模型，利用ADV测量三维流速，是国内最先对“Y”型交汇河道进行物理模型试验研究的，并将实验结果与支流斜接干流型交汇河道进行了对比，发现两类交汇的水流分区现象相似，但“Y”型交汇水流向下游呈现出螺旋流向，且螺旋趋势随支流流量增大而减弱。其后，他的学生针对90°“Y”型交汇河道也进行了一系列的研究。冯亚辉[26]基于郭维东的物理模型试验，研究汇流比对螺旋流流向和强度的影响，发现“Y”型交汇后水流下游的顺时针螺旋流的强度大于逆时针螺旋流；沿水流方向，螺旋流强度减弱；随汇流比增加，正负螺旋度值相应地增加。吴迪[27]在此基础上，给水槽增加0.15 m高的滩地将模型改为复式断面，研究得到复式断面与普通断面的“Y”型交汇河道水动力特性总体相似，也存在螺旋流，以逆时针方向为主，并发现交汇口处水面出现两侧凸起、中间凹陷的形态，添加滩地部位的水面出现支流侧凸起、干流侧凹陷的形态；滩地周边水体的剪切应力分布极不平衡，远离滩地则分布较均匀。

2.1.3支流入汇弯曲干流型

付中敏[28]等在国内初次建立顺直支流与弯曲干流相交汇的物理模型，采用ADV测速分析交汇角与汇流比对弯曲干流型交汇河道的水流运动特性的影响，发现交汇口附近出现水流分离区和涡旋环流区，且其范围均随交汇角和汇流比的增加而扩大，水流断面的横比降绝对值也随之加大。之后，贾猛[29]也对弯曲型交汇进行了水力特性研究，分析了不同汇流比和交汇角对交汇口附近及弯曲河道的水力影响，得到交汇后水流环流强度随交汇角变大而加强，水体之间的掺混程度、动量交换剧烈程度也随之加强，且环流旋度最值位置向下偏移；弯曲河道的凹面纵比降与汇流比成正比，而横比降与汇流比成反比。

综合以上参考文献，交汇河道水动力特性研究中较典型的物理模型试验研究概况见表1。

表1 交汇河道物理模型试验研究概况

2.2 数值模拟和理论分析方面

随着社会科学技术的突飞猛进，关于水流水力特性方面的数值模拟研究也方兴未艾。目前，紊流流场的数值模拟方法主要有：直接数值模拟(DNS)、大涡模拟(LES)、雷诺时均法(RANS)、重整化群模型(RNG)、投影法(PM)、格子玻尔兹曼方法(LBM)等。国内外通过数值模拟来研究交汇口水动力特性的起步较晚，但发展迅速且成果较为丰富，主要集中在一维平面与二维水深平均方面的数值模拟。

2.2.1支流斜接干流型交汇河道

较为经典的有Wang[30]利用三维数学模型模拟了德克萨斯州休斯顿中2条天然河流交汇口洪水演进过程，将简化的移动边界算法纳入模型以确定移动的流体区域，求解了曲线坐标系下的雷诺平均N-S方程并计算三维速度场和交汇河口的自由水面，利用数值模拟现有的和建议的河道几何形状进行速度变化的评估，并讨论了河口地形和现有结构对流场的影响。Babarutsi[31]利用3种不同的数学模型对交汇水流进行数值模拟来研究交汇口的掺混特性，将数值模拟结果分别与物理模型试验结果进行对比，发现单尺度湍流模型适合模拟偏向小规模的湍流交汇，并且对单尺度湍流模型的系数进行修正可以提高整体模型的性能和精度，将小尺度湍流和大尺度湍流作为独立分量的双尺度湍流模型模拟得到的结果与试验结果的吻合度高于把这两者作为一个整体的单尺度模型。

Ghostine[32]等对直角交汇水流分别用一维数学模型和二维数学模型进行了数值模拟，将数值模拟结果分别与试验数据对比，发现一维数值模拟误差较大，且在非恒定流的情况下并不实用。Khan[33]利用平面二维数学模型对交汇口进行了无河床高差的二维非恒定流水流的数值模拟，并与实验室收集的河道分叉和交汇的水槽数据进行对比，表明模拟的主支流的自由水面和主支流的流量比以及分支中的再循环区的宽度和长度等均与试验数据吻合得较好。

Bradbrook[34]使用三维数值模型模拟有、无河床高差的交汇河道，并探讨2个支流在速度和深度比不同组合下的情况，模拟不同边界条件对流场结构的影响，得到的结果与经验数据进行对比，表明在特定的深度和速度比的组合下，交汇口会出现二次流。Bradbrook[35]还利用大涡模型对交汇水流的周期性进行模拟，模拟的结果与试验数据进行比较，表明模拟能够捕捉一些关键流程的周期性，该模型提供了详细的流动和混合的数据，能帮助理解在汇流处产生和演化的大尺度湍流特征。

Biron[36]等采用三维数学模型对河床高程一致和不一致的交汇口以及交汇后水流混合过程进行数值模拟，表明交汇后的混合过程主要受河道平面曲率的影响。Kesserwan[37]等基于当弗劳德数较低时交界处的能量方程可以近似源头平等阶段的假设，在现有的理论组合模型的基础上对明渠交汇进行亚临界流动模拟，得出结论，即使弗劳德数谱是亚临界的，在处理能量源头平等时也必须采取预防措施，尤其对于弗劳德数大于0.35的交汇河道。

Song[38]认为在传统的浅水模型中二次流的三维特性由于深度平均处理通常会被丢失，但在弯曲或交汇的渠道中可以部分恢复垂直方向上的二次流速度剖面，所以对明渠水流的浅流模型中的二次流进行研究，结果发现压力梯度项是触发速度分布的主要因素，随着弗劳德数的增加，沿通道曲率形成的对流加速度在速度分布中被激活作为一个次要因素，而黏性应力失去了它的影响，底部摩擦的影响也较小。Shakibainia[39]等建立三维数学模型对交汇水流进行了较全面的数值模拟，研究结果表明，交汇水流的流动结构和自由水面的变化受交汇角、汇流比、宽度比和弗劳德数的重要影响，是由于这些因素影响着水流的流速和二次流的分布。

国内的相关研究中，茅泽育[40]等通过理论分析交汇口水流的影响因素，分析不同交汇角下动量修正系数与汇流比的相关性，探讨交汇前后水流水深比的理论公式，并与试验结果进行对比，给出了适用于数值模拟非恒定流内边界条件的交汇水流一维数学模型。赵升伟[41]等利用水深平均H-L模型、标准K-ε紊流模型针对交汇水流多数是缓流的流动特性，分别建立二维水流数学模型，采用TDMA(Time Division Multiple Access)时分多址逐行扫描法来求解方程，根据交汇口几何特征来对网格进行分区划分，并用实测资料对两种模型进行验证和对比，得出两种数学模型均能较好地模拟交汇水流的流动特性，但H-L模型在计算分离区的范围时考虑了逆压梯度边界层的影响，其结果会比K-ε模型更为精准。

冯镜洁[42]等对不同汇流比与交汇角组合下的交汇水流进行三维数值模拟，选用K-ε模型模拟水流的流速场和VOF(volume of fluid)模型模拟液体的自由面，模拟出交汇口近右侧有分离区和回流现象，分离区的大小与交汇角和汇流比成正相关。

周晶[43]利用雷诺时均模型(RANS)对直角等宽的交汇水流开展了数值模拟，研究不同汇流比下交汇区域水流流速场的规律，以及交汇角的改变对其的影响，发现水深比的变化随汇流比增大趋向平稳，但分离区范围变小；自由水面随交汇角加大而加剧，分离区范围也变大，二次环流强度加剧。

刘盛赟[44]等采用三维K-ε模型，建立水气两相流数学模型，用于交汇水流的水动力学研究，模拟不同交汇角、汇流比、动量比等对水流的影响，发现分离区的尺寸随交汇角、汇流比、动量比的减小均变小，且壅水现象减弱。王凯[45]通过应用动量方程，假定其他水力要素不变，计算分析不同汇流比和不同交汇角对交汇口处上下游水面线的影响趋势和程度，发现交汇角是影响交汇口处附近水面线的主要因素，且交汇角越大，对水面线的影响越大，对交汇后河道的泄流能力影响也越大。

魏文礼[46]等采用大涡模拟模型(LES)对不同交汇角度的明渠交汇水流进行数值模拟来研究水力特性，使用半隐式SIMPLE(Semi-Implicit Method for Pressure-Linked Equations)算法求解速度与压力耦合方程组，采用VOF法模拟自由水面，将90°的模拟结果与物理模型试验结果对比，发现吻合良好，继续用LES模拟不同交汇角的交汇水流，得到交汇口处横断面流速不均匀系数与交汇角成正比，即水流流速分布随交汇角增大越发不均匀。之后，魏文礼[47]等分别采用LES模型和K-ε模型对不同汇流比下交汇水流的水力特性进行数值模拟，使用同样的数值计算方法，将2种模型计算出的纵向截面水面线与物理模型试验结果进行比较，得出大涡模型(LES)结合VOF法能更好地捕捉交汇口水面的波动情况，通过比较2种模型计算得到特征横断面上的流线图，表明LES模型能较好地捕获水流瞬时流动特性，动态再现二次环流结构，更好地模拟交汇口附近的水动力特性分布规律。

2.2.2“Y”型交汇河道

冯亚辉[48]等采用雷诺应力输运方程模型(RSM)，数值模拟了“Y”型明渠交汇水流，选用有限体积法(FVM)离散格式与交错网格上的H-V校正算法，求解交汇后水体的流速与水深等参数，进行水流结构和雷诺应力分布的探究，再次证明了“Y”型交汇口附近存在流速回流和分离区，其范围与汇流比成反比，雷诺应力在水流中分布不均，较大值出现在分离区中。郭维东[49]等采用同样的方法进行研究，重点研究不同汇流比和交汇角对分离区的影响，并给出相应函数关系式和规律分布。

王晓刚对“Y”型交汇水流进行了较全面的数值模拟研究。为研究“Y”型交汇口处的壅水规律，王晓刚[50]把“Y”型交汇河道划分为单一顺直段与水流交汇段，并分别建立能量方程和动量方程进行求解，据此建立一维数学模型，验证合理后，利用该模型对“Y”型交汇口的各种主要水力控制因素进行了分析，结果发现水深比Hr随着汇流比增大，先变大到一个临界值后变小；当交汇角较小时，对Hr的影响不大，但当交汇角超过90°时，Hr随交汇角增大而急增；同时，Hr也随着下游干流弗劳德数Fr增大而变大，随着下游干流宽深比的增大而变小。其后，王晓刚继续研究“Y”型交汇口附近螺旋流的结构特征，通过三维数值拟分析了河床高差[51]和汇流比[52]对“Y”型交汇口附近螺旋流结构特征的影响，得到结论为河床高差的存在会削减主流近大流量侧的螺旋流强度，但会增强主流近小流量侧的螺旋流强度；交汇前存在流量差异的水流在交汇后，会在近大流量侧呈现较大趋势的螺旋流，另一侧会出现受挤压的螺旋流，当两者流量大小相近时，交汇口处会出现双重汇聚的螺旋流，并给出了“Y”型交汇的三维视图概化模型。

杨泽一[53]采用商用FLUENT软件建立三维水流数学模型，研究天然交汇河流在不同汇流比情况下的水动力特性，发现交汇口区域出现正负相交的涡旋，正涡旋的强度与汇流比成反比，负涡旋的强度随汇流比增加先衰减后加强；并在概化模型中探讨了汇流比对“Y”型交汇的影响，其结果与王晓刚[52]相同。

综合以上参考文献，归纳总结出交汇河道水动力特性探究中，较典型的数值模拟研究概况见表2。

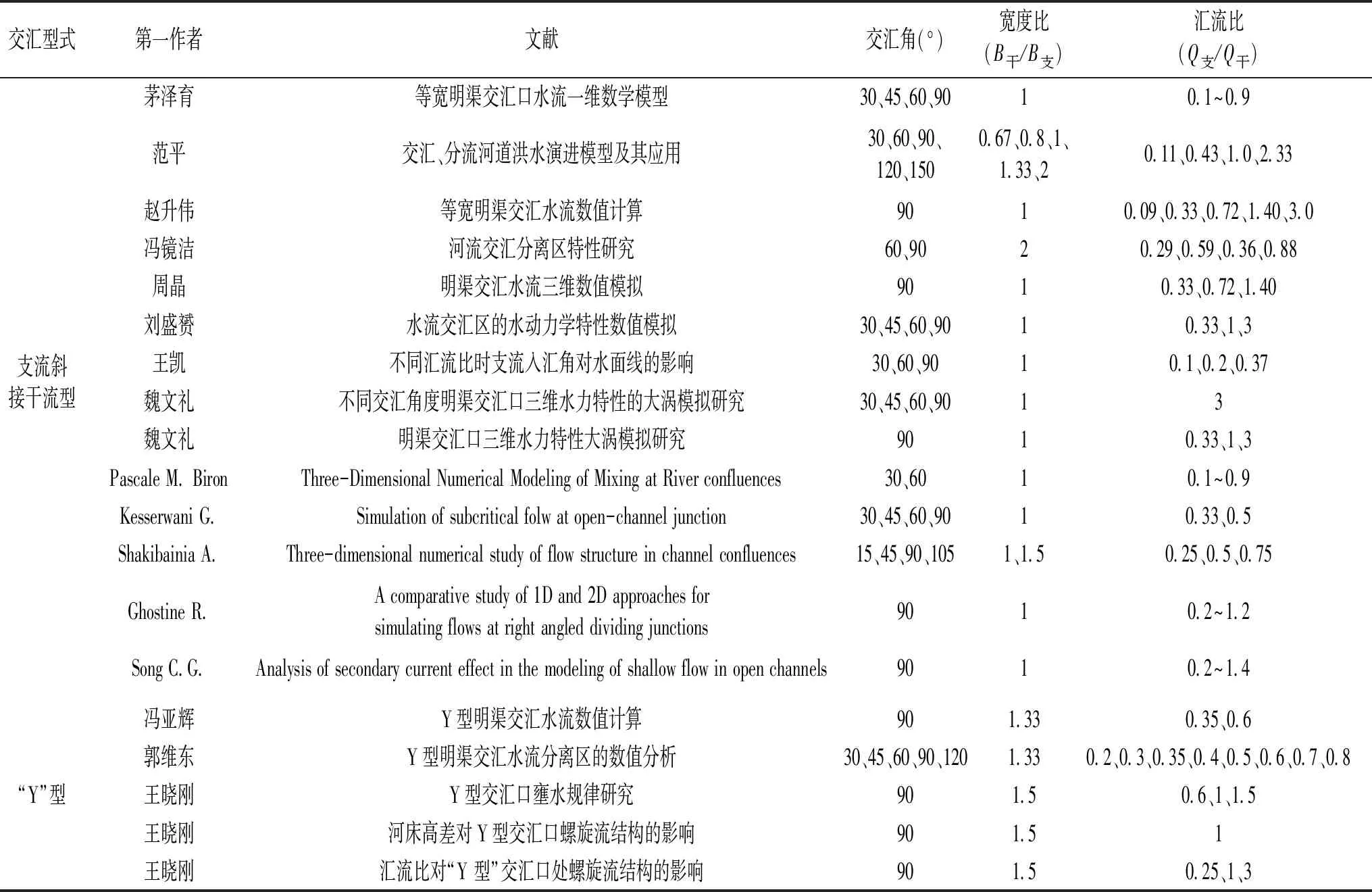
表2 交汇河道数学模型计算研究概况

3 交汇河道污染物掺混规律的研究现状

目前国内外对交汇口污染物输移掺混规律的研究不多，主要是通过数值模拟进行定性的描述和少数通过物理模型试验进行基础性的探究。关于河道交汇处污染物的研究，国外较典型的有Biron、Schemel、Binelli、Ribeiro等，国内较典型的有韩龙喜、华祖林、顾莉等。

Biron[36]等利用三维水流数学模型，分别对天然交汇河道和室内交汇明渠的污染物混合过程进行了数值模拟，结果表明在实验室内当干支流存在河床高差时污染物混合过程较快，而在天然交汇河道中交汇口近区的混合主要由上游来流流量决定，来流流量较小时混合较快，远区的混合主要由交汇后河道的弯曲程度决定。Isabel[54]等建立三维水动力模型来模拟不同流动状态对葡萄牙杜罗河河口污染物扩散的影响，并通过水位、流速、盐度和温度等数据来校正模型，发现高度变化的流动会降低水体分层并提高海水入侵，而稳定的流动最有利于污染物扩散，表明水流流动特征对污染物扩散有重要影响。

Schemel[55]使用锡尔弗顿附近的酸性矿井水作为天然示踪剂，对科罗拉多河中的交汇河道进行污染物输移掺混规律的研究，通过测量相应位置的电导率，计算出参照示踪剂与天然示踪剂的混合率百分比的中位值，分析得到示踪物质在该交汇河道下的分布情况和输移掺混规律。Ribeiro[56]等通过野外实测和水槽模型试验相结合的方式，研究90°交汇河道的水动力特性和污染物混合规律，通过加大支流宽度探究其对汇流形态的影响，利用罗丹明作为示踪剂，分析各试验工况下交汇水流的二维浓度分布特征，发现随着主支流流量比不变的情况下，拓宽支流宽度有利于污染物混合，提高汇流带的生态价值。

Binelli[57]采用多重生物标志物表征的方法，对天然交汇河道的污染物混合迁移规律进行了分析研究，采集交汇前后春秋两季的水样，在实验室监测天然生物斑马贻贝中的各指标参数(单细胞凝胶电泳、过氧化氢酶、超氧化物歧化酶的活性等)，还评估了几种有机污染物(多环芳烃、多氯联苯、六氯苯等)的生物累积，根据各参数的监测值来分析污染物质在水流中的输移掺混规律，该方法较为新颖。

早在1995年，郑庆华[58]等人率先采集珠江口中咸水与淡水交汇区内的水和沉积物，在实验室进行自净试验，探索其自净过程和变化规律，发现水体中NO3-N含量在低盐度水中降解较快，而NO2-N、NH4-N、PO4-P含量变化与盐度无明显关系，氮和磷的沉积百分率与悬浮物含量成正比，与有机质含量成反比，丰水期比枯水期更有利于污染物的自净。同年，张银英[59]等人在此基础上，按是否加入污染物和流动或静止的条件组合进行试验，探究珠江口的淡水与咸水交汇区中CODMn、油类、砷的自净规律，发现这几种污染物中石油降解最快，其次是砷、砷的含量变化与水的盐度有明显的关系，其自净速度在低盐度水中比高盐度水中快，水流运动比水流静止更有助于污染物自净。

洪益平[60]利用深度平均K-ε紊流数学模型，对三峡水库中河道交汇段进行了水力特性和污染物输移特性的数值模拟研究，在中国较早利用数学模型对天然交汇河道进行污染物混合特性研究。茅泽育[61]等人参考了洪益平的研究，认为利用标准K-ε紊流模型不能很好地反映分离区的真实形态，因为没有考虑到分离区中有部分水流逆向回流，故而针对此缺陷，重新选用H-L紊流模型研究交汇水流的流动特征，结合污染物输运方程建立污染物输运模型，选用FVM的离散格式与交错网格上的H-V校正算法来求值计算，运用天然交汇河道的实测资料进行模型验证，表明该方法能较好地模拟表征交汇水流的流动特征和污染物的输运规律。

刘雪兰[62]选用二维有限元(FEA)数学模型对长江、嘉陵江交汇的重庆段进行水动力与水质模拟，对FEA模型采用地表水模拟系统(SMS)进行数据处理和计算，模拟发现交汇口附近有涡旋流动，水流掺混剧烈，有回流现象，易造成污染物滞留，水流在污染物排放口一侧会形成高浓度污染带。周富春[63]等人也采用平面二维数学模型，根据概化的数值区域，模拟了长江与嘉陵江交汇区中污染物的混合，研究了污染物输移掺混规律，利用排污量、排污口位置和保证率等作为变量因子，组合进行模拟，分析得污染带的长度与污染物的排污量成正相关，顺直河段污染带较狭长，弯曲段污染带较宽，故顺直河道比弯曲河道更有利于污染物输移掺混。

魏娟[64]等人认为交汇水流存在自由水面的变化，会对流速场和污染物扩散有一定的影响，所以选用水气两相流数学模型，模拟水流在有自由水面水深变化下的流速和浓度分布，以不同汇流比和交汇角设置模拟工况，发现污染带的狭长程度与汇流比和交汇角均成反比，并且表明污染物浓度分布主要受水流流速的影响，尤其在交汇掺混区间。李娟[65]等利用二维水动力水质数学模型对汾河入黄河河口的水动力特性与污染物(COD)扩散进行数值模拟，根据水文水质资料，设置汇流比工况为0.014、0.016以及0.018，模拟结果表明，污染物COD总体分布在一个狭长的区域内，在横向迁移上扩散起主导作用，在纵向迁移上既有对流又有扩散，且对流作用远大于扩散作用，河口滩面积随汇流比的减小而减小，污染带变长。

韩龙喜[66]等建立物理模型并与数值模拟相结合，对“两进两出”十字型汊口水流流场和水质的平面二维分布规律进行了探究，表明各出流断面的污染物浓度有很大的差异，并重新定义了十字型汊口进、出断面污染物浓度的响应关系以及响应系数的计算公式，与用以往的三级联解法计算得到的响应系数进行对比，表明新方法误差更小，结果更优。袁航[67]通过建立45°支流斜接干流型的交汇水槽物理模型，对该类型交汇水流的流场和浓度场的分布规律进行研究，并在此基础上，通过三维K-ε紊流数学模型，探究了不同交汇角和汇流比对水力特性和污染物混合特性的影响，并计算分析了交汇河道的横向混合系数，表明水流交汇区会产生二次环流，对污染物混合有很大的影响，横向混合系数随汇流比的增大而减小，曲线随交汇角增大而变陡峭，并加入植物来探究其对交汇河道横向混合系数的影响。

4 结语

河道交汇广泛存在于自然界中，研究交汇河道的水动力特性和污染物掺混规律对河网水环境污染治理有重要的实际意义。但是，当前对于交汇河道的研究在诸多方面还有待完善。

a) 从河道交汇分类角度看，现有研究主要集中在支流斜接干流型。根据兰波于1998年的统计分析，认为山区河流中支流斜接干流型与“Y”型2类交汇口的数量相当，且“Y”型汇流口的水力特性与支流斜接干流型存在许多不同之处，必然导致其污染物输移掺混规律有别于支流斜接干流型汇流口，亟需开展相关研究。此外，对于支流斜接干流型的研究绝大多数为支流入汇顺直干流型，而对于支流入汇弯曲干流型与支流入汇分汊干流型的相关研究较少，而这2种类型的汇流口在自然界中亦很常见，其水动力特性及污染物混合规律与支流入汇顺直干流型有较大差异。因此，需要深入研究支流入汇弯曲干流型和支流入汇分汊干流型交汇河道水力特性与污染物输移掺混规律。

b) 水槽物理模型试验是当前交汇河道研究的主要手段，取得了较为丰富的研究成果。然而，实验室研究成果与天然河流研究成果存在较大不同。如在实验室水槽中可以明显观测到分离区的存在，这在天然河流汇流口中却很少能观测到。在汇流口下游横断面流速的分布、流速方向、水流脉动强度、紊动动能等也存在分歧，目前对此没有较为合理的解释。原因可能在于天然河流存在很大的宽深比，河床地形复杂，干支流水流存在水温、密度差异等，更系统全面的研究有待进一步开展。

c) 天然河道中往往存在水生植物，而植物对于河流的水流特性与物质拦截等存在一定影响。Li C W[68]评估了柔韧性和叶面对流动阻力的影响，结果表明，植被的灵活性降低了植被诱导的流动阻力和垂直雷诺剪切应力，且叶子的存在进一步增强了这些减少效果。同样在河道交汇处往往水生植物丰富，植物对其水力学特性与污染物的输移掺混也存在影响。已有顺直及弯曲河道中植物对水动力及污染物混合特性方面的研究成果，未来需要深入研究考虑植物影响下的交汇口水流特性与污染物输移掺混规律。

d) 河道交汇区域是溯流鱼类及当地鱼类迁徙的关键部位，汇流口水流特性与水生生物物理栖息条件密切相关，在流域生态系统中具有突出地位。汇流口也是营养物、木质残骸及其他有机物聚集的地方，在河流高水位期间，汇流口周围淹没的河漫滩也是幼鱼避难的场所。1999年Braaten[69]证实支流的入汇可使汇流口鱼类增多，2004年Fernandas[70]等人发现交汇河流对鱼种类的多样性有重要的影响。目前交汇河道的水力特性对于水生态系统的影响研究尚处于起步阶段，随着河流生态保护认识和要求的提高，未来可望成为本领域热点研究方向之一。