《用计算器探索规律》教学设计
2019-03-27蒋小凌
蒋小凌
【教学内容】
苏教版四年级下册第42 页第四单元第2 课时。
【教学过程】
一、复习引入
1.复习旧知。
师:上节课,我们认识了计算器,学会了用计算器进行计算。
出示题目:用计算器计算下面各题。
1236-564= 546×25=
1548÷43= 326+1856÷29=
学生独立完成。完成后,指名学生回答,并说说计算时的注意事项。
2.游戏激趣。
师:同学们,你们喜欢做游戏吗?我们用计算器玩“猜数字”游戏。从“1~9”这9 个数字中选一个你喜欢的数字记在心里,不能说出。接着,在你的计算器上连续输入9 次,然后用它除以“12345679”,把得数告诉老师,老师就能知道你最喜欢的数字是几。同学们,相信吗?请你试一试。
3.导入新课。
师:今天我们要用计算器来寻找算式中蕴含的规律,探索其中的奥秘。(板书课题:用计算器探索规律)
【设计意图:利用游戏导入,激发学生的学习兴趣和求知欲。同时,也为新知设疑,为本节课的学习埋下伏笔。】
二、探究规律
1.教学例3。
出示第42 页例3。
26640÷111=________
26640÷222=________
26640÷333=________
学生读题,并要求用计算器独立计算。
交流汇报得数,教师板书。
26640÷111=(240)
26640÷222=(120)
26640÷333=(80)
2.观察比较,发现规律。
师:观察这三道题之间有什么关系,有没有什么规律呢?
请将下面两题和第一题比较,看被除数、除数和商是怎样变化的,你有什么发现?完成表格。小组讨论,交流发现。
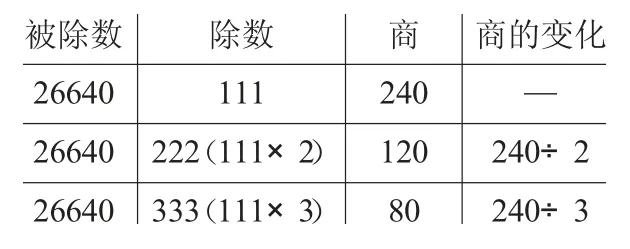
被除数 除数 商 商的变化26640 111 240 —26640 222(111×2) 120 240÷2 26640 333(111×3) 80 240÷3
交流:你发现什么规律吗?
生1:第二道题和第一道题相比,被除数不变,除数乘2,商等于原来的商除以2。
生2:第三道题和第一道题相比,被除数不变,除数乘3,商等于原来的商除以3。
小结:被除数不变,除数乘几,得到的商就等于原来的商除以几。
3.运用规律并验证。
引导:如果除数继续变化,商会怎样呢?这个规律适用于其他算式吗?(出示后四道题)
26640÷444= 26640÷555=
26640÷666= 26640÷888=
根据发现的规律,你能直接填出下面各题的得数吗?
学生直接填写得数。
提问:填写这几道算式的得数时,你是怎么想的?
填写的得数对不对呢?请你用计算器验算,看做对了没有。
4.归纳小结。
通过计算器计算,我们发现在除法算式里,被除数不变,除数乘几,得到的商就等于原来的商除以几。反过来,被除数不变,除数除以几,得到的商就等于原来的商乘几。
【设计意图:引导学生经历“计算器计算—发现规律—应用规律—计算器检验”的探索过程,初步体验除法算式中商的变化规律,体会计算器强大的计算功能,积累一些探索和发现简单规律的经验,感受数学的形式美和结构美,激发用计算器计算的兴趣。同时,帮助学生进一步加深对除法运算的理解,又有利于学生体验探索规律的过程,积累归纳、类比等数学活动经验,感受学习成功的喜悦。】
三、巩固练习
1.完成“练一练”
出示第42 页“练一练”。
111111÷37037=
222222÷37037=
333333÷37037=
444444÷37037=
666666÷37037=
999999÷37037=
(1)先让学生用计算器算出前三题的得数,交流并呈现得数。
教师板书:
111111÷37037=(3)
222222÷37037=(6)
333333÷37037=(9)
(2)观察、比较算式中各数的变化。
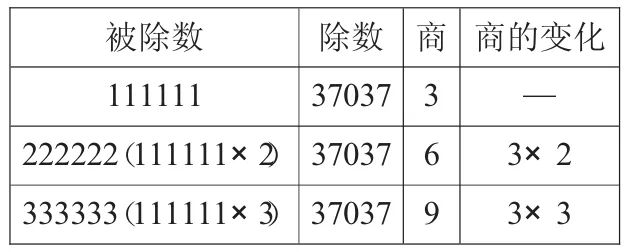
被除数 除数 商 商的变化111111 37037 3 —222222(111111×2) 37037 6 3×2 333333(111111×3) 37037 9 3×3
(3)提问:比较这几道算式,你发现了什么规律?
学生发现:除数不变,被除数乘几,得到的商就等于原来的商乘几。
(4)应用规律完成后三题,并说说你是怎样想的。完成后,再用计算器验证。
【设计意图:让学生再次经历探索和发现规律的过程,并在这一过程中进一步体验由特殊到一般、由此及彼的认识过程,积累探索简单数学规律的经验,感受计算器的学习与应用价值,增强探索意识和创新意识。】
2.完成“练习七”第6 题。
(1)出示题目。

4 9 2 3 5 7 8 1 6 49+35+81 18+53+94 42+37+86 68+73+24 38+51+76 67+15+83 492+357+816 618+753+294
要求学生结合方格中的数,观察每组算式的特点。
交流:你发现每组算式的特点了吗?各有什么特点?举例说一说。
引导说出:这里的每道算式里的数都是按表里各数排列位置的相应顺序列出的。每组里两道算式的数字和符号顺序正好相反,把其中一道算式的数字和符号的顺序倒过来,就是另一道算式。
(2)计算比较,发现规律。
让学生计算每道算式的得数并填写。
提问:比较各道算式的得数,你发现了什么现象?
引导:你能再写出一组这样的算式吗?自己再列出一组两道连加算式,算出得数,或者一组三位数连加的算式计算。
交流:你列的什么算式,得数是多少?
提问:这里的算式和得数符合你发现的规律吗?你对上面这些算式和计算有什么感受?
(3)分析表格,延伸思考。
大家感觉这里的计算非常有趣,提问:你发现什么了吗?方格中横行、竖行和斜行的三个数的和是多少?
三个数的和都是15,三个两位数的和是165,三个三位数的和是1665。它们之间有什么规律呢?感兴趣的学生课后可以讨论。
【设计意图:本题取材于我国古代神话传说中的“洛书”,它是世界上最古老的幻方,是我国古代劳动人民智慧的结晶。本题重在发展学生观察、比较、分析、类比、归纳的能力,感受数学的神奇和美妙,激发对数学学习的兴趣。】
3.完成“练习七”第8 题。
1×9+2=
12×9+3=
123×9+4=
1234×9+5 =
______×____+____=______
______×____+____=______
让学生先用计算器算出前四题的得数,再直接填写后两题横线上的数。
交流:前四题的得数是多少,后面两道题的算式和得数是怎样的?你发现了什么规律?算式中的各数分别有什么规律?
【设计意图:让学生通过计算,观察总结出算式各部分的关系,进一步巩固用计算器进行四则混合运算的步骤和方法,积累一些类比与归纳推理的经验,发展初步的合情推理能力。】
4.游戏揭秘。
师:同学们还记得老师在课的开始和大家做的“猜数字”游戏吗?
完成本题后,你就知道其中的奥秘了。
出示题目。
111111111÷12345679=
222222222÷12345679=
333333333÷12345679=
444444444÷12345679=
555555555÷12345679=
学生用计算器计算。
你发现了什么规律?和同学说一说。
运用规律,你还能再说出一些算式吗?
【设计意图:此环节与本课的游戏激趣相呼应,揭秘题中的奥妙。联系算式之间的规律,学生豁然开朗。鼓励学生说出更多的算式,培养学生的应用能力。】
四、全课总结
这节课你有哪些收获?请与同学们分享。
