RELAX和BP算法在电机转子故障诊断中的应用

闵天文,金银平

（三门峡职业技术学院，河南 三门峡 472000）

0.引言

电机作为生产和生活中广泛使用的动力设备，有着不可替代的重要作用。但是在其长时间的工作过程中，由于受到工作环境、负载变化、电源电压波动、运行机制等方面的影响，容易出现线圈导线的老化、性能下降，导致电机故障的产生。其中常见的故障包括转子断条、定子绕组匝间短路、轴承磨损及气隙偏心等[1]，如果不能及时准确地发现这些故障并进行诊断修复，很可能造成严重的经济损失，甚至是人员伤亡。因而对电机故障诊断系统的研究具有十分重要的经济与社会效益。

鼠笼式异步电动机转子断条故障信号的主要特征频率由于与基波频率十分接近，所以很容易淹没在强大的基波中，从而导致故障的诊断困难。因此需要借助现代信号分析与处理的理论和技术手段来消除电源基波频率对转子断条故障特征的影响从而能够有效的对故障特征信息进行凸显和提取。

常用的信号特征提取方法如下：（1）基于瞬时功率谱分析法、基于矢量控制原理法以及基于Park's矢量法[2-3]，这些方法因为需要采集多相电压、电流信号，软、硬件的开销较大，虽然是将基波成分转变成了直流，断条故障特征频率转变成2ksfo在一定的程度上使故障特征得到了突出，但依然存在与直流分量十分接近的问题。（2）基于相关抵消法[5]，该方法是取出线电压中与基波电流相位相近的一个分量，然后再跟电流的转换值相减，可以在一定程度上减少基波的影响，但是效果不够明显。（3）Hilbert模量的频谱分析法[6]，能将基波成分转变成直流，在单个故障时能够突出故障特征，但是因为存在平方运算，在发生复合故障时易产生交叉项。

RELAX算法[7-8]是一种对加性噪声以及系统误差假设可松弛的谱估计算法，它用于分离混合信号中的特殊信号分量，只需要利用FFT变换来实现，并且依据非线性最小方差(NSL)准则，准确地估计出信号的各参数，从而准确描述出基波信号并剔除。

因此将RELAX算法应用到鼠笼式异步电动机的故障诊断中，从而有效地消除基波信号对转子断条故障特征的影响，同时提取出准确有效的故障特征数据，并通过BP神经网络对这些故障特征数据进行识别，已达到对电机故障进行准确诊断的目的。

1.算法研究

1.1 信号模型

对于正常运行中的异步电机，理论上讲定子相电流中只会含有基波分量，当然因一些制造水平等方面的原因，也会含一些谐波，但其幅值很小，基本可以忽略。此时相电流的数学表达式为：

式中：Im1为基波幅值；ω1为电源角频率； 为基波初相位。

当转子发生断条故障时，在定子电流中会产生频率为fbro(k)=(1±2ks)f1的故障特征，其中当k=1,2,3……。发生偏心故障时，在定子电流中将产生频率为fec(m)=(f1±mfr)的故障特征，其中m=1,2,3……。f1为电源基波频率，fr为转子旋转频率，其中fr=(1-s)f1/P(s)(s为转差率，P为电机极对数)。由上述分析可知，异步电动机发生转子故障情况下定子电流的通用表达式[9]为：

式中：Ipk、Ink分别为断条故障时，特征电流的幅值，k=1,2,3……；Ipm、Inm分别为偏心故障时，特征电流的幅值； 分别为上述电流分量的初相；e(t)为均值为零的白噪声。

1.2 RELAX算法

RELAX算法逐个地剔除或者清除信号的各分量，并且通过迭代方法尽量确保每一个分量估计值的准确性[10][11]。

假设某种信号是由D个加性的信号源所组成，考虑有噪声存在的情况下，其数学表达式可以写为：

式中：N表示信号时域采样点数；bj表示第j个信号的幅值参数；sj(n)表示第j个信号的波形参数；c(n)是加性噪声，均值为零，并且与关注的信号彼此统计独立。

假设已得到前d-1个信号的幅度及波形参数估计值，那么含第d个信号的剩余信号的数据矢量应表示为：

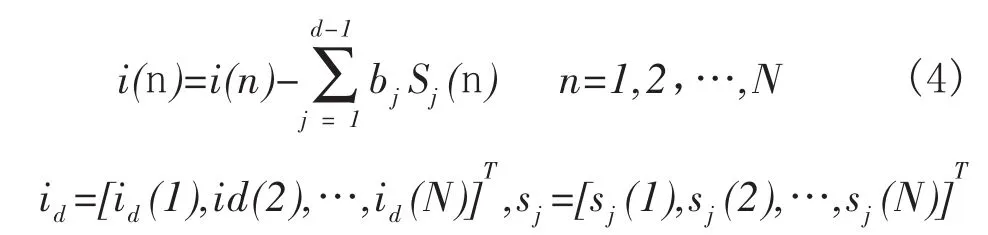
依据非线性最小方差准则，令

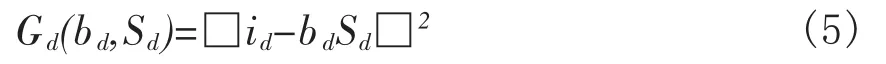
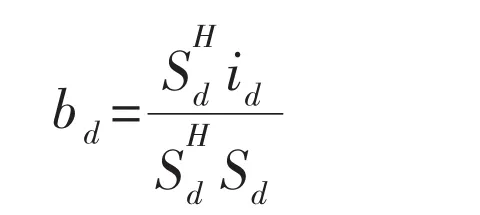
其中，SdH为 Sd的共轭转置，将式（6）代入式（5），得

于是可得

该算法可利用对的FFT变换后的最高频谱幅度对应求出波形参数的估计值。

1.3 RELAX算法迭代过程

第一步：假设d=1，则id(n)=i(n)，依据式(6)、(8)可得到第一个信号的幅值b1和波形参数的估计值。

第二步：假设d=2，依据第一步得到的b1和S1，结合公式(4)得到含第2个信号的数据矢量i2，再依据式(6)、(8)可以得到第2个信号的幅值b2和波形参数S2的估计，再依据得到的b2和S2，结合公式 (4)可以得到含第一个信号的数据矢量，进而再重新估计b1和S1，反复迭代到收敛为止。

第三步：假设d=3，依据第二步得到的b1和S1，b2和S2，结合公式(4)可得到含第三个信号的数据矢量i3，再依据式(6)和(8)可得到第三个信号幅值b3和波形参数S3的估计。再由前面所得的 b3和 S3，b2和 S2，结合公式(4)、(6)、(8)重新估计 b1和 S1，再依据 b1和 S1，b3和 S3以及公式(4)、(6)、(8)来重新估计 b2和 S2，再依据 b2和S2，b1和 S1，结合公式(4)、(6)、(8)来重新估计 b3和S3，如此反复迭代到收敛为止[12]。重复上面的步骤直至d与给定的信号数D相等。

2.系统设计

2.1 系统结构

为了实现电气隔离，电流信号由电流传感器型号为TA539来进行采集；系统采用型号为S3C2440的ARM处理器芯片，其主要作用是用RELAX算法程序对采集的信号进行处理，来获取故障特征信号；由于S3C2440的A/D转换电路只允许0～3.3V电压，所以经调理后，信号被调整到0～3.3V范围内，才能送至ARM处理器，然后将采集得到的数据以串口通讯的方式传给PC机处理。系统的整体结构如图1所示。

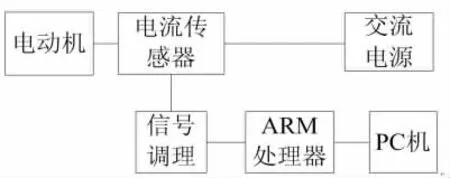
图1 系统结构图

2.2 系统软件流程

在PC机上通过Labview设计出电机故障诊断系统，整个系统设计分为两步：第一步设计故障诊断系统界面，主要用来显示频谱分析曲线和故障诊断结果；第二步通过BP神经网络设计一个分类器，来对采集的数据进行处理，实现故障的诊断。系统程序流程如图2。

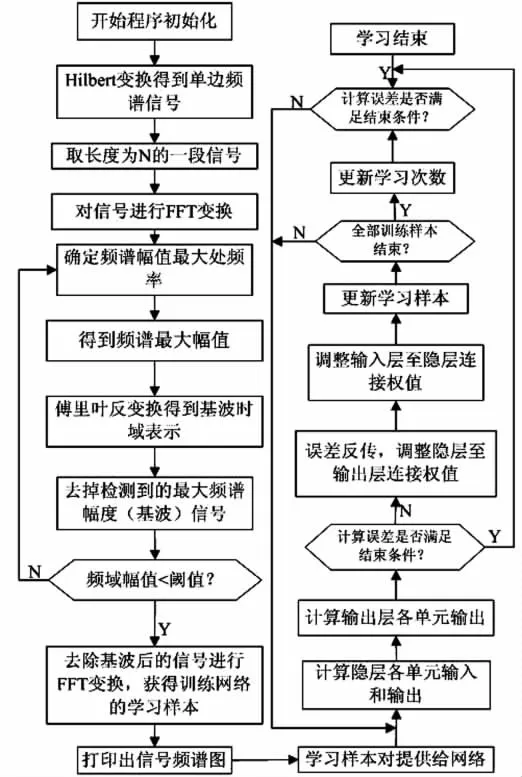
图2 系统程序流程图

式(9)中A为输入神经元数目，C为输出神经元数目，δ而为一个大于1小于10的常数，通过反复试验最终确定隐含层神经元数目为6。隐含层的激活函数选择tan sig(S型正切函数)，输出层激活函数选择logsig(S型对数函数)。

3 仿真实验

仿真实验以定子电流故障信号模型为基础，在matlab中通过RELAX和BP算法程序对信号进行特征提取和故障诊断，系统采样频率设为10000Hz，电机详细参数见表1。

其中BP网络[13][14]参数选择设计依据如下。

根据电机的运行状态确定输出神经元个数为3，三种状态分别是：1、转子正常用神经元输出(1,0,0)表示，2、偏心故障用(0,1,0)表示，3、1根断条+偏心故障用(0,0,1)表示。隐含层神经元的个数通过式(9)来确定：

表1 电机参数

分别对转子无断条加偏心和1根断条加偏心这两种情况下采集的单相电流进行频谱分析和用RELAX算法剔除基波后的频谱分析，结果如图3、图4。两组图中的(a)图表示没剔除基波前的频谱图，(b)图为剔除基波后的频谱图。

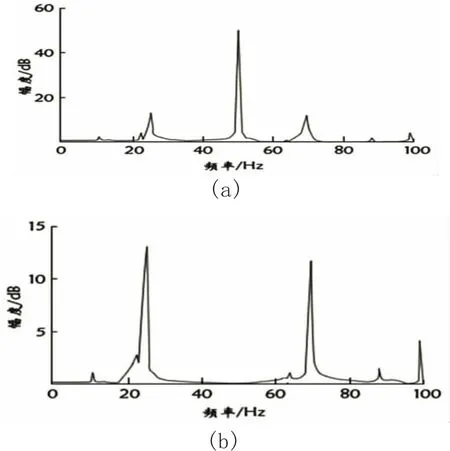
图3 转子无断条+偏心剔除基波前后的频谱图

图4 转子1根断条+偏心剔除基波前后的频谱图

从图3和图4看出，混合信号内的基波分量基本被剔除，从而使故障频率的到了明显的突出。尤其从图4(a)看出，当转子一根断条故障时，断条故障特征很微弱，所以很容易被强大的基波所淹没，而从图4(b)则可知RELAX算法有效地剔除了基波分量避免了故障特征被淹没情况发生。利用提取的故障特征对BP神经网络进行训练，然后对训练好的网络进行测试，得到网络的训练误差曲线如图5。

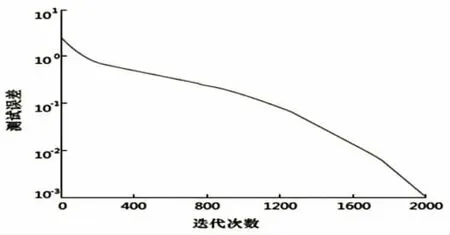
图5 网络测试误差曲线

从误差曲线可知，训练误差达到了预先设定的误差标准并最终收敛，因此根据BP神经网络实际输出，并结合故障特征的分类得到结果如表2所示。

表2 仿真输出结果

从表2可知，网络的实际输出结果符合实测信号对应的电机运行状态，结果表明了利用RELAX算法能够对故障特征数据进行有效的提取，并且对BP神经网络训练后，可以实现对电机故障状态的准确分类。

4.结论

本文以转子发生故障时的定子电流数学模型为基础，将RELAX算法和BP神经网络应用到对其故障早期的诊断中，通过RELAX算法消除了电源基波成分对故障特征成分的影响，有效地突出了故障特征，并且通过训练好的BP神经网络故障识别系统，对电机转子断条、偏心故障进行了自动准确的识别，因此为鼠笼式异步电动机的早期的故障诊断提供了有效的手段，具有一定的工程应用价值，本文只是对功率较小的小型异步电机进行测试，对于是否适用于大功率的复杂电机还有待进一步深入研究。