一种提高DTW算法运算效率的改进算法∗

谢扬扬 娄渊胜 商国中

（河海大学计算机与信息学院 南京 211100）

1 引言

通过对水文时间序列相似性的分析我们可以得到水文数据的特点，理解水文数据变化的规律，并且回答了在防汛指挥中经常被问到的一个问题“在历史上什么时候出现过同当前情况相似的水文过程？”水文时间序列的相似性度量是水文序列相似性搜索的一个必须的环节，目前在水文时间序列的相似性度量常采用的方法是动态时间规整距离，它可以有效地处理沿时间轴上形变的问题，具有很好的鲁棒性，被越来越多的应用到水文领域的相似性度量中。

在实际应用中，传统动态时间规整算法直接采用动态规划，计算复杂度为O（mn），其中m，n为时间序列的长度，复杂度过高。目前国内外学者针对DTW复杂度高的问题的进行研究，主要的方法有：1）提前终止技术，当累计的规整距离超过阈值时，停止剩余路径的搜索；2）采用全局约束设置搜索范围，将搜索路径控制在规整窗口内部［3］。

本文通过分析现有的DTW算法，在此基础上对平行四边形规整窗口外画出三个矩形，对路径进行快速修剪，矩形外的点都不需要再做计算，减少了计算量，在一定程度上提高了算法运算效率。该算法进一步缩小了规整路径的搜索范围，在一定程度上减少了原算法的计算量，从而达到运算效率上的提高，尤其是在两个时间序列的长度较长时，这种运算效率的提高显得更加的明显。

2 DTW算法

2.1 DTW算法描述

动态时间规整算法的主要思想是对两个需要进行相似性比较的时间序列Q（q1，q2，…，qi，…qn）和C（c1，c2，…，cj，…，cm），构造一个在时间上对齐的n*m维矩阵D（其中n为Q的长度，m为C的长度，通常n≠m）。矩阵D中的元素di，j=（qi-cj）2代表Q中点qi和C中点cj之间的欧式距离［1］。在距离矩阵D中运用动态规划的思想从起点d1，1到dn，m之间找到一条累计距离最小的路径，这个距离就是动态规整距离，如图1所示。动态时间规整路径L需要满足的条件有：1）有界性：max（m，n）≤ L ≤ m+n。2）规整路径的起止点为距离矩阵斜对角线的两端的元素。3）连续性：路径L中的元素是连续的。4）单调性：规整路径L经过某一点（i，j）的前一点必须是（i-1，j），（i，j-1），（i-1，j-1）三点中的一点。

图1 动态时间规整路径图

2.2 规整窗口约束的DTW算法

对于距离矩阵D中的元素不需要全部参与计算和决策，运用全局约束不仅可以加速DTW算法的运算时间，而且可以防治时间序列的病态规整［4］。学者Itakura提出一种平行四边形的规整窗口约束如图2所示。认为在动态时间规整距离的计算中，平行四边形外的点不需要参与运算。在实际应用中通常把k1设为1/2，k2设为2。由于E点和斜率已知，容易表示出平行四边形的四条边。

有学者提出把动态弯折分成三段：（0，Xa）、（Xa+1，Xb）和（Xb+1，N），其中：取最接近点的整数，可以得出M、N的限制条件：2M-N ≥3、2N-M ≥2。

当M、N的长度不满足条件时，认为两个时间序列不适合进行动态时间规整相似性度量。在现有的DTW算法中，需要构建距离矩阵和累计距离矩阵，即使已经通过平行四边形规整窗口限制了搜索范围，但搜索的每一步都需要与四条边进行边界计算，运算量依然非常大，当两条时间序列很长时，这种重复的计算严重消耗时间和资源［12］。

图2 平行四边形约束

3DTW算法改进

3.1 现有算法存在的问题

现有DTW算法中，需要计算两个时间序列之间的距离矩阵和累积距离矩阵，计算量很大，即使在限定了规整路径的搜索范围处于平行四边形范围中的情况下，路径搜索的每个环节都要进行上下边界的计算，计算量依然很大，尤其是在两个时间序列很长时，这种重复性的计算就越多，严重地降低了算法的效率。因此我们需要对算法做出进一步改进，提高它的运算效率。

3.2 改进算法的原理

在运用规整窗口约束后，需要判断哪些点在规整窗口范围内，这时要进行N*M次计算，判断其是否在范围内。为了快速地确定平行四边形的约束范围，避免大量的边界运算［8］，如图3所示设计出三个矩阵S1、S2、S3。Xa在数值上等于A点横坐标，Xb在数值上等于B点横坐标。这时只需要在矩形范围内对点进行边界值判断，并且只需计算平行四边形OAEB中点的距离和累计距，大大减少了计算量。因为E点的坐标E（N，M）和OA，OC直线的斜率已知，点A，B，G，H的坐标都可以求出：

由于平行四边形的形状在斜率一定的情况下，由N，M的长度决定，可能会出现Xa=Xb，或者Xa＞Xb的情况。为了更准确地限制范围，即在各种情况下使三个矩形面积和在包含平行四边的前提下最小，在此提出另外一种设计方式，如图4所示。

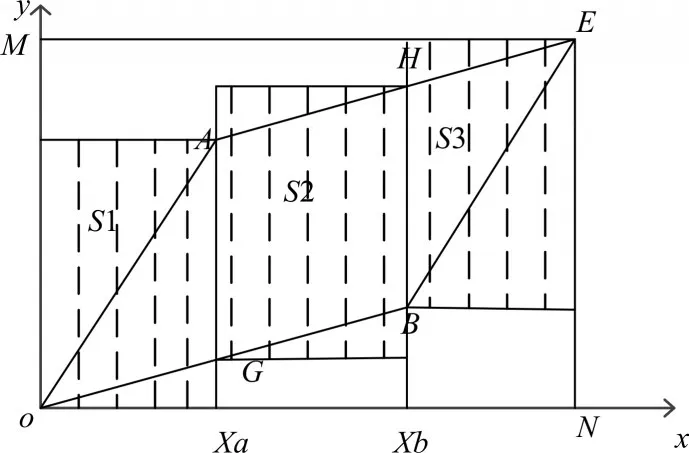
图3 改进的DTW范围约束1

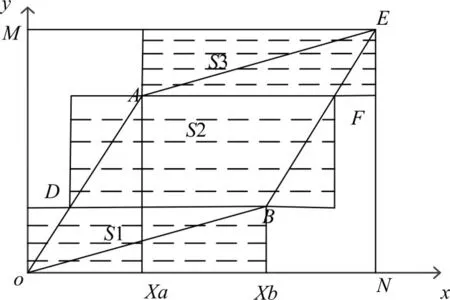
图4 改进的DTW范围约束2

3.3 改进算法适用范围

下面根据Xa、Xb的大小关系，说明在各种情况下两种设计方式中矩形面积和的大小关系：

1）Xa＞Xb

如图3、图4所示三个矩形面积和分别为Sa、Sb，通过计算得：

2）Xa=Xb

当Xa=Xb时，即A点横坐标的值等于B点横坐标的值，A点和B点在同一垂线上只能采用图4所示的方式。

3）Xa＜Xb

如图5、图6所示。

图5 Xa＜Xb时适用范围1

图6 Xa＜Xb时适用范围2

通过计算得：图5矩形面积之和Sc与图6面积矩形面积之和Sd的关系：

Sc-Sd=8N2+3M2-10MN得出如下关系：

这两种设计方式在本质上是相同的，目的是为了在包含平行四边形的前提下使规整窗口最小，减少计算量，在实际应用中应该根据两条水文时间序列的长度关系，判断使用哪一种方式。

3.4 改进算法实现

以两个时间序列 R=（r1，r2，r3，…，rm），T=（t1，t2，t3，…，tn）为输入，改进的DTW算法实现如下：

36：if（m＜n）｛

37：method_column（）；

38｝

39：｝

40：if（［（2m-n）/3］=［2（2n-m）/3］）｛

41： method_row（）；

42：｝

43：if（［（2m-n）/3］＞［2（2n-m）/3］）｛

44：if（（m＞2n）||（m＜［（4n）/3］））｛

45： method_row（）；

46：｝

47：if（4n/3≤m≤2n）｛

48：method_column（）；

49：｝

50：｝

51：for i=0；i＜ n；i++

52：for j=0；j＜m；j++

53： if d［i］［j］==0.0

54： continue；

55：if i==0&&j==0

56： D［i］［j］=d［i］［j］；

57： elseif i==0&&j！=0

58： D［i］［0］=d［i］［0］+D［i-1］［0］；

59： elseif j==0&&i！=0

60： D［0］［j］=d［0］［j］+D［0］［j-1］；

61：else

62： warpDistance=min（D［i-1］［j］==0.0 ？：+∞，D

［i-1］［j-1］）==0.0 ？：+∞，D［i］［j-1］）==0.0 ？：+∞）

63： warpDistance+=d［i］［j］；

64：D［i］［j］=warpDistance；

65：return warpDistance

上述改进的算法中，d［n］［m］为距离矩阵，D［n］［m］为累积距离矩阵，可以看到，三个矩形区域外的格点对应到两个二维矩阵中元素值没有被计算，算法最终返回的warpDistance为规整路径的距离，也就是DTW算法所要求出的最短扭曲距离。

4 实验结果与分析

4.1 实验环境

实验环境：Eclipse+java，JDK1.7；

系统参数：P320 AMD Athlon（tm）ⅡP320 Dual-Core Processor，CPU 2.10GHz，RAM 4GB，32 位Windows7旗舰版操作系统；

编码语言：java语言；

实验数据：本文实验的数据选取滁河金牛湖滁红山窑闸水库的日平均水位作为数据集。

4.2 实验过程

实验过程：为了能在不同长度段的时间序列上验证传统动态时间规整算法和改进的算法运算效率。

数据选取：

1）1972年1月1日至1974年3月31日长度为90和1971年1月1日至1971年4月30日长度为120的时间序列；

2）2000年1月1日至2000年12月31日长度为366和1998年4月1日至1998年12月31日长度为275的时间序列；

3）2001年1月1日至2005年12月31日长度为1826和2006年1月1日至2010年12月31日长度为1826的时间序列；

4）1990年1月1日至1998年12月31日长度为3287和2000年1月1日至2009年12月31日长度为3653的时间序列。

对数据预处理并将其规范化在［0，1］区间。每两个时间序列进行5次试验，总共有四组对比数据，分别计算这四组两种算法下运算时间的平均值，试验结果如表1。

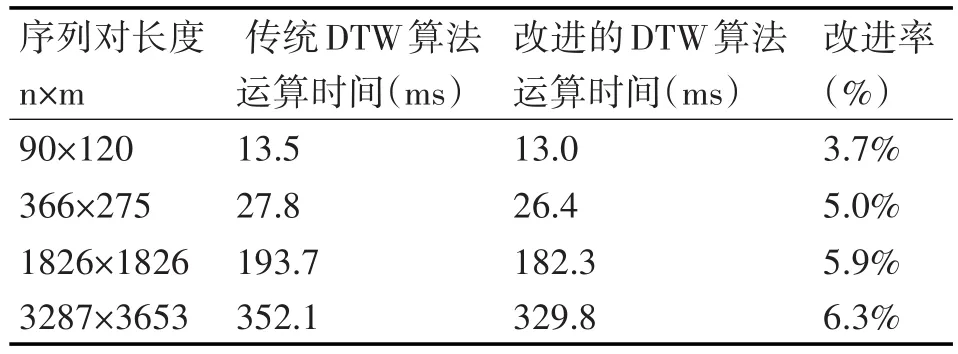
表1 两种算法下的运算时间比较

4.3 实验结果

通过表1可知：当时间序列对长度为90×120时，改进后的算法提高的时间百分比为3.7%；当时间序列对长度为366×275时，改进后的算法提高的时间百分比为5.0%；当时间序列对长度为1826×1826时，改进后的算法提高的时间百分比为5.9%；当时间序列对长度为3287×3653时，改进后的算法提高的时间百分比为6.3%；因而可以证明本文提出的改进算法，在一定程度上减少了计算量，提高了算法的运算效率，尤其是当两个时间序列较长时，这种运算效率上的提高更为明显。

5 结语

DTW算法思想是采用动态规划技术来求解最优化问题的过程，将一个复杂的全局最优化问题分解为许多局部最优化问题，并一步一步地进行决策［14］，最终得到全局问题的一个最优解，在时间序列相似性匹配过程中体现为利用局部最佳化寻找一条路径，沿着这条路径，两个时间序列之间的累计规整距离最小。但是在进行DTW距离度量两个时间序列时，由于DTW算法采用逐点匹配的方式，所以很容易受到时间序列中的“噪音”和“孤立点”的干扰［13］，并且当匹配的时间序列的长度过长时，计算量非常大。因此，寻找一个合适的约束条件，有效地控制两个时间序列的匹配范围，成为提高DTW匹配结果精确度和缩短匹配时间的关键。

本文在分析现有的DTW算法基础上，在平行四边形路径搜索范围外，规划出三个矩形区域，矩形区域外的格点不会出现在规整路径中，因此无须进行格点是否在平行四边形范围内的判断，因此在一定程度上减少了计算量，提高了算法的运算效率。通过上表我们可以看出，改进后的算法不仅减少了运算的时间，在一定程度上还提高了运算效率，尤其是在时间序列很长时效果更加明显。本文DTW改进算法的本质是缩小规整窗口的范围，减少没必要的重复计算，所以算法在准确度上并没有降低。