复合材料层合管等效抗弯刚度的试验分析

沈泽懿

摘要：开展了4种铺层碳纤维复合材料层合管的短柱试验和4点弯曲试验，得到了2种试验方法下试件的等效抗弯刚度。通过建立轴压作用和弯曲作用下层合管的有限元模型，分析了4种铺层试件纤维方向应力分布特征，从材料纤维方向不同拉压模量角度分析了两种试验方法下等效抗弯刚度存在差异的原因。分别通过分层材性赋值和基于截面拉压应力区域比重的近似等效模量赋值，利用理论预测模型计算得到了等效抗弯刚度，理论值与试验值相差10%以內，验证了材料纤维方向弹性模量赋值方法的可行性。

关键词：层合管;等效抗弯刚度;四点弯曲试验;短柱试验;弹性模量

中图分类号：TQ050.4⁺3文献标识码：A 文章编号：1001-5922（2019）07-0113-07

大长细比的复材杆件整体稳定荷载与欧拉临界荷载相近，且长细比越大，欧拉公式的预测精度就越高。只要抗弯刚度计算准确，Euler公式能够准确预测试件的整体稳定性。此外，等效抗弯刚度（模量）作为构件的基本参数，获取该参数的准确值对复材构件整体稳定性计算至关重要。复材构件等效抗弯刚度的求解可归结为2种方法：第1种方法为等效弹性模量法，该方法是基于抗弯刚度是构件的基本属性的认识，即认为无论构件受轴压还是受弯，其等效抗弯刚度均可表示为E·I，而I是截面的基本属性，只与截面形式和几何尺寸有关，这样求解等效抗弯刚度问题就转化为求解等效弹性模量问题，其方法一般是采用轴心受压构件计算模型或短柱试验进行求解。第2种方法为整体求解法，即认为等效抗弯刚度是弯曲构件的基本属性，作为一个不可分割的参数[EI]出现，一般采用构件弯曲计算模型或弯曲试验进行求解。

在实际的计算或试验过程中，上述2种不同的出发点造成复材构件等效抗弯刚度的获取方法显得缺少依据，文献也未对其进行详细说明，如Goodman对3根硼/环氧FRP圆管进行了轴心受压试验研究，研究表明大长细比的杆件整体屈曲荷载与欧拉屈曲荷载相近，其中弹性模量E通过短柱轴压试验确定;Hewson研究了拉挤GFRP槽形构件在轴压作用下的弯曲屈曲，利用Euler公式计算构件的弯曲屈曲荷载时，纵向弹性模量E由弯曲试验测得。钱鹏对12根拉挤GFRP圆管的轴心受力性能进行了试验研究，通过短管受压试验确定GFRP管的轴向弹性模量E。本文将通过复合材料层合管的短柱试验和四点弯曲试验，对比分析2种获得等效抗弯刚度的方法，并结合常用的理论预测模型，分析基于上述2种试验方法的等效抗弯刚度存在差异的原因。

1 实验材料及方法

1.1基本原理

1）短柱试验

根據短柱试验的荷载位移曲线即可计算得到管件的等效弹性模量

式中P为轴压荷载，l为杆长，A为杆件横截面面积，△l为杆件轴向位移，r_ou和r_in分别代表管件的外半径和内半径。

2）四点弯曲试验

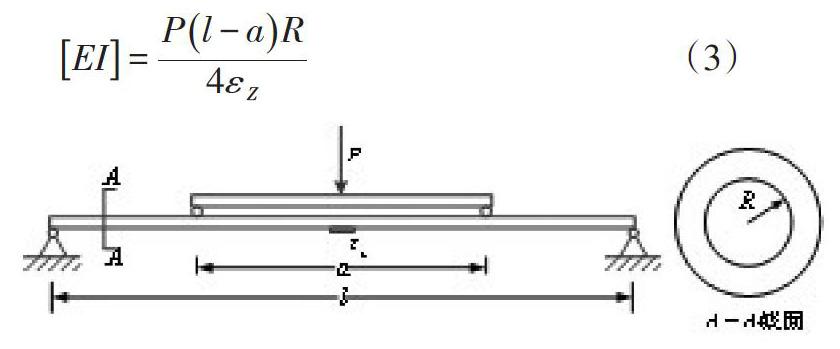
试验装置如图1所示。试验需要采集的数据包括有效长度l，分配梁两个荷载点的距离a，外半径R，施加的荷载P，管件底部中间位置的应变值ε_z。由四点弯曲试验求解抗弯刚度的公式为：

1.2材料性质与试验设计

材性试验使用的试件是采用模压工艺制作的1，5mm厚碳纤维单向板。试验包括：拉伸试验参照GB/T3354-1999标准，分为0°、90°两个方向;压缩试验参照GB/T 856-2005标准，分为0°、90°两个方向;面内剪切试验参照ASTMD7078-2012标准，分为垂直和平行纤维两个方向（注：获取Elc的单向纤维板0°方向压缩实验为补充实验，与其他数据获得的实验样本非同一批次）。CFRP单向板工程弹性常数如表1所示。

短柱试验和四点弯曲试验均设计了4种铺层的试件，试件几何参数、铺层形式、试件/测点等相关数据如表2所示。短柱试验对应试件编号为S18-6-A、S18-6-B、S18-6-C、S18-6-D，通过CDT105微机控制电子压力试验机加载，加载速率为1mm/min，如图2所示。四点弯曲试验对应试件编号为L18-6-A、L18-6-B、L18-6-C、L18-6-D，在试件中部设置成正交的2个测点，每个测点采集4组应变数据。四点弯曲试验的试件计算长度l=580mm，分配梁加载点间距a=400mm，两端铰支座和分配梁加载如图3所示，试验铰支座由半圆形凹槽和圆柱形滚柱组成，为了较好的模拟铰支条件，试验中在凹槽内涂抹黄油。

2 试验结果

表3中E为试件短柱试验等效轴压模量的试验值，为了便于比较分析，将等效轴压模量与截面惯性矩相乘得到试件的等效抗弯刚度EI。从表3可以看出，试件的等效轴压模量试验值离散系数均在8%以内，试验结果较为稳定;单向纤维S18-6-A组试件的平均轴压模量为86.1GPa，与材料1方向压缩模量E_lc相差9.4%，说明单向0°纤维试件应存在初始缺陷，如纤维弯曲、纤维间微裂缝等;其他3种铺层的等效轴压模量基本相同，说明外侧环裹层的角度对其影响不大。表4中[EI]为根据四点弯曲试验数据得到等效抗弯刚度（为了与短柱试验区分，体现该方法直接获得等效抗弯刚度，用[EI]表示），可以看出外侧环裹层角度越小，等效抗弯刚度越大。

3 实验结果分析

通过短柱试验得到试件等效轴压模量而计算得到的等效抗弯刚度值与由四点弯曲试验直接得到的等效抗弯刚度值（平均值）对比情况如图4所示，可以看出对于单向纤维铺层[O₆]试件，两种试验方法获得的等效抗弯刚度相差最大达到38%，其他铺层形式相差最小也达到了10%，且均为短柱试验值偏小，由此可以说明利用短柱试验方法获得等效轴压模量进而计算试件等效抗弯刚度的方法趋于保守。

为了分析等效抗弯刚度数值存在差异的原因，现建立两类试验有限元模型，利用ANSYS软件SOL-ID185分层实体单元建模，该单元无实常数，采用截面命令定义层截面数据，包括层厚度、材料、纤维方向、厚度方向积分点个数，利用命令EORIENT将单元坐标系。轴旋转为管件径向，并通过命令CERING和MASS21单元建立刚域实现管件简支边界条件和集中荷载的施加。在轴压模型、四点弯曲模型中，分别以P=100MPa和P=100N为例进行说明。图5为轴压荷载下管件截面沿壁厚方向纤维方向（1方向）应力的分布情况，除[O₄/90₂]铺层试件以外，其他试件每一铺层纤维方向应力均为负值，即承受压应力，说明其变形主要受压缩弹性模量控制。对于四点弯曲，4种铺层试件的纯弯段截面上每一铺层纤维方向上应力分布如图6所示，可以看出截面上（包括每一铺层上）纤维方向拉压应力均有分布。

从材料基本力学性质（如表1）看，轴向拉伸模量要比轴向压缩模量大（文献给出的碳纤维材料材性参数亦如此），弯曲试件纤维方向拉压均存在，而轴压试件纤维方向均受压（除[O₄/90₂]外），因此可以定性说明四点弯曲试验获得的等效抗弯刚度较短柱试验获得的等效抗弯刚度大。

为了进一步定量说明纤维方向上拉伸模量和压缩模量对抗弯刚度的影响，选用两种理论预测模型分别计算等效轴压模量和等效抗弯刚度。文章以Choucha-oui模型计算等效轴压模量，以张恒铭漠型计算等效抗弯刚度，前者采用了能够获得铺层精确应力应变场的三维弹性理论，后者采用了符合复合材料圆形管件梁真实变形的变形理论，两种方法均经试验验证且计算精度较高。轴压工况下，层合管件由于轴对称特征其应力状态沿环向不变，即每一铺层应力状态相同，因此根据实际应力状态（拉压状态）对[O₄/90₂]铺层管件每一鋪层单独赋材料属性，即0°铺层赋值E₁=E_1c，90°铺层赋值El=E_1t，其他铺层管件E₁=E_lc。四点弯曲工况下，由于每一铺层纤维方向上均正负应力均存在，为便于物理方程计算，纤维方向等效弹性模量E₁按公式（4）近似计算。

E₁=E_1c·V_c%+E_1t·V_t% （4）

其中V_c%表示横截面铺层上纤维方向上压应力区域所占的比重;其中V_t%表示横截面铺层上纤维方向上拉应力区域所占的比重。根据四点弯曲有限元模型中划分单元纤维方向应力的正负号，计算拉压应力单元所占的比重来分别代表V_t%和V_c%，表5是4种铺层试件纯弯作用下V_t%、V_c%值以及根据式（4）得到的等效E₁。

将等效E1代人张恒铭模型，将分层赋值的E1代人Chouchaou模型分别计算4种铺层复合材料管等效抗弯刚度如表6，从表6可以看出：两个理论计算模型对抗弯刚度的预测精度均较高（短柱试验中由于试件本身可能存在纤维初始弯曲等缺陷导致试验值偏小，从而与理论预测模型值相差10%），说明在两个理论计算模型中对E₁的赋值符合管件的实际受力状态，是可行的，从而进一步从数值上验证了短柱试验相比四点弯曲试验获得的等效抗弯刚度要小是由于拉压状态下材料不同的弹性模量引起的。目前在很多研究工作中，复合材料单向板的材性数据往往只给出纤维方向拉伸作用下的弹性模量作为材料的E₁，基于该弹性模量的等效抗弯刚度理论预测值将明显偏大（如张恒铭糢型、文献民模型等），以L18-A和L18-D两种工程中常用铺层试件为例，将公式（4）计算出的等效E₁和E_1t分别代人理论预测模型中并和试验值进行对比，如图7所示，可以看出E_1t下两种铺层试件等效抗弯刚度理论预测值较试验平均值分别大15%和20%，从而导致整体稳定计算与设计偏于不安全。

4 结论

1）针对试验方法获取用于复合材料构件整体稳定性计算的等效抗弯刚度（等效弹性模量），四点弯曲试验较短柱试验更准确，短柱试验值较四点弯曲试验值小10%-38%，但短柱试验值仍可用于保守、偏安全的工程设计。

2）对于单向纤维0°铺层试件，四点弯曲试验对纤维弯曲等初始缺陷的敏感性要小于短柱轴压试验。

3）针对文中4种铺层碳纤维圆管试件，等效抗弯刚度的短柱试验值小于四点弯曲试验值的原因是碳纤维材料纤维方向拉伸模量大于压缩模量。

4）利用理论模型预测等效抗弯刚度或等效弹性模量时，轴压工况下可根据每一铺层的实际应力状态对物理方程中纤维方向弹性模量进行赋值，弯曲工况下可根据公式。

5）计算纤维方向等效弹性模量代人物理方程。基于上述纤维方向模量选取方法，采用文献两个抗弯刚度理论模型预测值与试验值相差均在5%以内（单向纤维试件由于初始缺陷相差10%）。