基于粒子群算法的高速列车节能研究
2019-03-24何之煜杨志杰吕旌阳陈汇远
何之煜,杨志杰,吕旌阳,陈汇远
基于粒子群算法的高速列车节能研究
何之煜1, 2,杨志杰2,吕旌阳3,陈汇远2
(1. 中国铁道科学研究院 研究生部,北京 100081;2. 中国铁道科学研究院 通信信号研究所,北京 100081;3. 北京邮电大学 信息与通信工程学院,北京 100876)
针对高速列车在多站间运行中的节能优化问题,对基于时刻表优化的冗余时间分配策略进行研究。根据列车的动力学模型和列车站间节能运行,建立以准点和能耗为目标的优化模型,利用粒子群算法对总的冗余时间进行合理分配,并根据适应度函数值变化进行迭代寻优。利用京沈线辽宁段实际的线路数据进行仿真计算,给出列车运行速度、能耗关于距离的曲线图,并与其他的冗余时间分配策略进行比较,结果表明,本文提出的算法可以在保证列车准点的情况下,降低整体运行能耗,证明了算法的有效性,为列车运行图的编制提供参考。
铁路运输;冗余时间;节能运行;粒子群算法

高速铁路运输系统的能耗主要源于电能的损耗,其中,列车牵引能耗的占比最大[1−3]。基于节能目标的列车运行操纵优化,在减少能耗的同时,还降低了系统运营成本。列车自动驾驶系统(Automatic Train Operation, ATO)作为列车自动控制系统(Automatic Train Control, ATC)的关键子系统,是提高高速铁路系统智能化和自动化的重要途径[4]。Milroy[5]以连续的牵引力、制动力作为控制变量,忽略线路坡度影响,建立基于最小能耗的列车动力学模型,为现代列车节能运行的研究奠定了基础。Asnis等[6−9]利用Pontryagin原理对列车运行最优操纵工况进行求解,得出在短距离运行时,列车节能操纵工况序列为最大牵引−惰行−最大制动,在长距离运行时,还应包括巡航工况。Khmelnisky[10]考虑连续变化的坡度以及限速条件,证明了在给定巡航速度的情况下,列车的最优运行曲线可以唯一确定。王青元等[11]针对控制量连续并考虑再生制动,利用伴随变量在工况切换中的微分方程,研究列车操纵工况的最优切换时机,为列车节能运行提供了参考。LI等[12]研究列车在不同操纵级位下的最优控制模型,提出列车运行时间与能耗呈负相关关系。吴洋等[13]通过实时调整列车运行间隔,增大站间运行时间以减少能耗。WONG等[14]基于客流量的实时需求,动态调整停站时间和站间运行策略,以达到节能的效果。黄友能等[15]在列车站间节能运行的基础上,利用时间裕度分配运行时间,用以指导运行图编制。YANG等[16]综合考虑再生制动利用和列车停站时间调整,建立多目标的运行图优化模型,从而减少运行能耗。基于以上研究,利用列车最小运行时分策略和站间工况转换节能操纵模型,通过设计粒子群算法,在总运行时分不变的情况下,以能耗、准时和舒适性等作为优化目标,建立基于运行图优化的高速列车节能模型,合理分配时间余量,以降低列车总体运行能耗。
1 问题描述
1.1 单列车站间运行模型
单列车站间运行模型实际上是一个多约束条件的优化问题,在给定运行时分、线路条件、限速信息等情况下,根据国内外专家学者深入研究的高速铁路节能操纵4阶段运行模型:最大牵引−巡航−惰行−最大制动,生成一条指导列车站间节能运行的曲线,如图1所示。
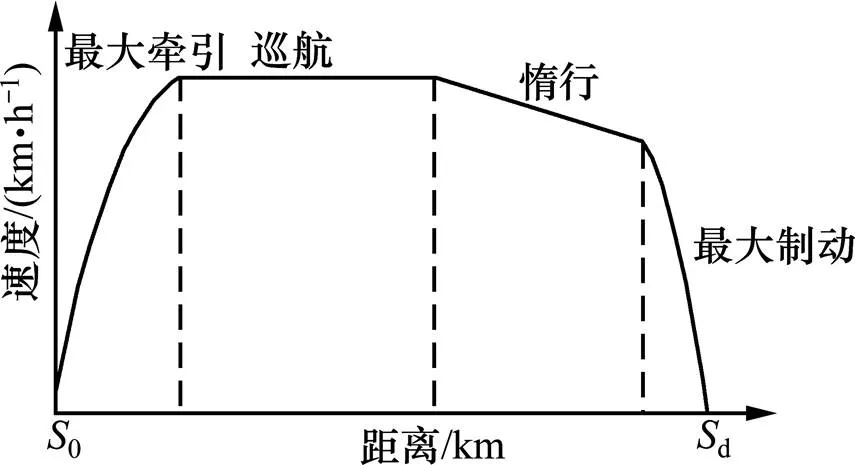
图1 列车节能运行曲线
结合线路条件和牛顿力学定律,列车运行动力学模型可以描述为:



式中:表示重力加速度,通常取9.8 m/s2;0,1和2分别表示列车的滚动摩擦系数,机械阻力系数和空气阻力系数。

式中:s,c和t分别表示单位坡道阻力、单位曲线阻力和单位隧道阻力,N/kN。
单列车站间受到的约束条件如下:
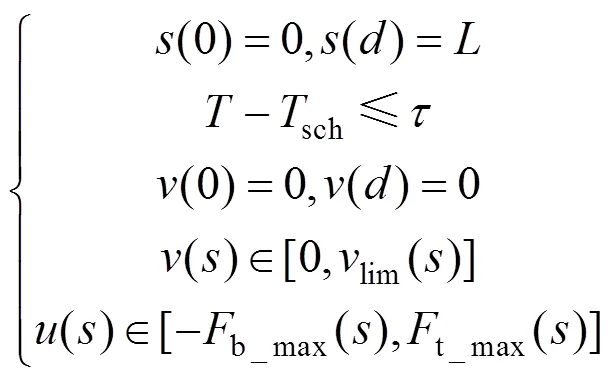
式中:表示站间距离,km;sch表示时刻表制定的运行时间,s;表示最大允许时间误差,s;lin()表示限速条件,km/h。
1.2 冗余时间优化分配的列车节能模型
列车运行图的制定需要根据实际线路的客流情况,来满足运力的要求。在站间运行时间的制定上,一般是最短运行时间策略加上一定时间的冗余。冗余时间的引入,一方面可以增强运行图的鲁棒性和灵活性,当列车在运行过程中受到干扰,而偏离预定的运行曲线时,可以快速通过调整运行策略恢复至原计划;另一方面,合理的冗余时间的分配可以有效减少列车运行能耗。
模型以列车总运行能耗和列车准点运行作为优化目标

式中:E(T)表示第个站间运行时间为T的能耗,kWh;表示列车运行站间的数量;()表示列车运行的总能耗,kWh。
列车总的运行时分需满足如下约束:
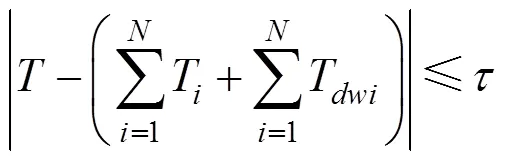
式中:T表示第个站间的停站时间。
根据文献[10],列车站间运行时间与能耗呈负相关关系,且能拟合成一个一元三次函数。但对于不同站间,受站间距、线路条件、不同限速等情况的影响,拟合出来的曲线也不相同。如图2所示,给出了站间A和站间B关于能耗−运行时间的关系曲线,A_min,B_min分别表示站间A和站间B的最小运行时分,A_max,B_max分别是其对应的最大能耗值。可以看出,对于不同的站间,分配相同的冗余时间得到的节能效果也不同。也就是说,不同的站间在得到相同的冗余时间∆时,对应的能耗−运行时间曲线上的斜率不同,由图3可以看出,∆A/ ∆>∆B/∆,因此冗余时间更多的分配给站间A的节能效果更好。对于列车多站间运行的情况,合理的冗余时间的分配有利于列车节能运行的决策。
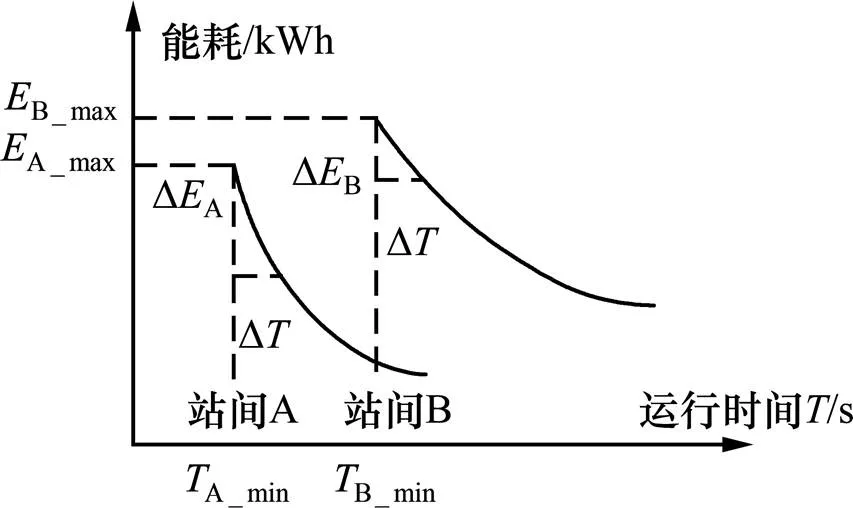
图2 冗余时间分配方法
2 基于粒子群算法的列车运行图优化
2.1 最小运行时分策略
冗余时间是列车运行图编制的站间运行时分与最小运行时分之差,它提高了运行图的鲁棒性和系统运输效能。本文中站间最小运行时分策略定义为:根据线路不同限速分成个区段,每个区段内限速相同,假设站间的起点和重点的限速值为0 km/h。若后一个区段限速值比前一个区段高,那么根据列车的牵引特性曲线和线路条件,自前一区段的末端以最大牵引工况加速至限速值,然后切入巡航工况;若后一区段限速值比前一区段低,那么根据列车的制动工况,自后一区段的起点以最大常用制动工况反推至前一区段限速值,列车的最小运行时分策略曲线如图3所示。

图3 最小运行时分策略
2.2 冗余时间优化分配算法
粒子群算法是Kennedy等[17]提出的一种简单高效的进化算法,通过种群内个体之间的协同来寻找最优解。首先,在系统状态空间中随机分布一群可行解,称为粒子,然后根据适应度函数求解出每个粒子的适应度,并不断更新粒子的速度和位置,通过当前粒子适应度与个体最优解和种群最优解的比较,并进行不断的迭代,求解出问题的最优解。根据单列车区间节能运行模型和运行图优化模型,在运行图总运行时分的约束下,以能耗、准点作为优化目标,定义列车运行时间偏差为:

定义归一化的关于准点的目标函数Φ为:

式中:T表示第个个体列车运行的总时间。
定义归一化的关于能耗的目标函数Φe为:
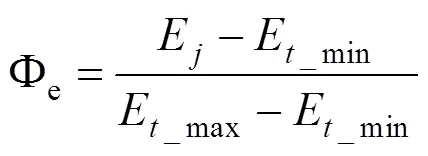
式中:E表示第个个体列车运行能耗;E_min表示种群中列车运行的最小能耗;E_max表示种群中列车运行的最大能耗。
因此,综合列车能耗、准点目标函数,定义基于粒子群算法的时刻表优化的适应度函数,
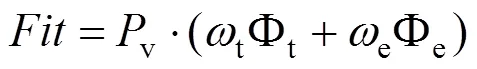


式中:p是一个大于1的正整数。
因此,算法的优化目标可以表示为:

运行图优化算法的实现步骤如下:
1) 初始化优化仿真的参数,包括列车参数,线路信息,种群个体数量,最大迭代次数。

3) 计算得到冗余时间T。

5) 根据各站间的运行时分,利用4阶段列车站间节能运行策略,优化生成节能运行曲线。并根据适应度函数求解每个个体的适应度值。
6) 通过比较更新个体最优解和种群最优解。
7) 利用粒子群算法更新粒子的速度和位置,

更新比例参数,并计算更新后的各站间运行时间。其中,惯性权重因子定义为

8) 如果迭代次数小于,返回步骤5。
3 仿真算例
以京沈线辽宁段部分线路作为仿真对象,线路区间为牛河梁站至沈阳西站,线路总长为355.9 km,线路最大坡度为−24.8‰,最大允许时间偏差为30 s。本文选取线路4站3站间来进行列车运行时间的优化分配,列车参数信息如表1所示。

表1 列车基本参数信息
利用线路信息、限速信息和列车参数等条件,根据最小运行时分策略,仿真求解出列车在各站间的最短运行时间如表2所示,总的运行时间为 4 834 s。为了保证时刻表的灵活性和鲁棒性,设计冗余时间为总的最小运行时分的10%,也就是483 s。本文提出的列车基于时刻表优化的节能策略,目标是通过将冗余时间合理分配至各站间,在满足准点的基础上,使总的运行能耗最低。

表2 站间最小运行时分
3.1 一般的冗余时间分配策略
一般的站间运行冗余时间分配策略分为2种:绝对分配和相对分配。前者是将冗余时间平均分配给各站间最小运行时分,然后利用四阶段节能运行策略实现能耗的降低。后者是按照各站间最小运行时分的10%,然后分配给各站间作为时刻表的运行时间。
首先,将线路运行冗余时间483 s平均分配给3个站间(策略1)。如图4所示,给出了3个站间速度、能耗关于距离的曲线。可以看出:3个站间的优化后的运行时间分别为1 571,2 962和790 s,总的运行时间为5 323 s,偏离总的运行时间6 s。在3个站间优化后的运行能耗分别为2 076.8,5 486.1和766.4 kWh,总的运行能耗达到8 329.3 kWh。

(a) 速度—距离曲线;(b) 能耗—距离曲线
然后,根据各站间的最小运行时分,按比例分配10%的冗余时间,也就是冗余时间分配分别为140,280和63 s(策略2)。如图5所示,给出了速度、能耗关于距离的曲线,可以看出,优化后的站间运行时间分别为1 545,3 081和709 s,总的运行时间为5 335 s,偏离时刻表运行时间18 s。优化后的站间运行能耗分别为2 140.4,5 362.2和991.3 kWh,运行能耗分别为总的运行能耗达到了 8 492.9 kWh,较之上一个分配策略高出2.0%。

(a) 速度—距离曲线;(b) 能耗—距离曲线
3.2 粒子群算法的冗余时间分配策略


(a) 速度—距离曲线;(b) 能耗—距离曲线
4 结论
1) 对于高速列车多站间运行场景下,以降低列车整体运行能耗为目标,研究在时刻表总运行时间不变的情况下,冗余时间的合理分配策略问题。基于列车动力学模型和列车站间节能运行策略,采用粒子群算法,对种群内冗余时间分配方案进行迭代优化。
2) 利用京沈线辽宁段实际的线路数据进行仿真,通过仿真结果,分析各站间运行时间和能耗变化,并与一般的冗余时间分配策略进行比较。结果表明,本文提出的优化分配算法,在保证列车准点的情况下,可以有效降低列车运行能耗,为运行图编制提供参考。
[1] YANG X, LI X, NING B, et al. A survey on energy-efficient train operation for urban rail transit[J]. IEEE Trans Intell Transp Syst, 2016, 17(1): 2−12.
[2] LU S F, Hillmansen S, HO T K et al. Single-Train Trajectory Optimization[J]. IEEE Trans Intell Transp Syst, 2013, 14(2): 743−750.
[3] SONG Y D, SONG W T. A novel dual speed-curve optimization based approach for energy-saving operation of high-speed trains[J]. IEEE Trans Intell Transp Syst, 2016, 17(6): 1564−1575.
[4] DONG H, NING B, CAI B G, et al. Automatic train control system development and simulation for high-speed railways[J]. IEEE Circuits Syst Mag, 2010, 10(2): 6−18.
[5] Milroy I. Aspects of automatic train control[D]. Leicestershire: Loughborough University, 1980.
[6] Asnis I, Dmitruk A, Osmolovskii N. Solution of the problem of the energetically optimal control of the motion of a train by the maximum principle[J]. USSR Computational Mathematics and Mathematical Physics, 1985, 25(6): 37−44.
[7] Howlett P G. An optimal strategy for the control of a train[J]. J Austral Math Soc Ser B: Applied Mathematics, 1990, 31(4): 454−471.
[8] Howlett P G, Pudney P J, Vu X. Local energy minimization in optimal train control[J]. Automatica, 2009(45): 2692−2698.
[9] Howlett P G, Cheng J. Optimal driving strategies for a train on a track with continuously varying gradient[J]. Austral Math Soc Ser B, 1997(38): 388−410.
[10] Khmelnitsky E. On an optimal control problem of train operation[J]. IEEE Trans Autom Control, 2000, 45(7): 1257−1266.
[11] 王青元,冯晓云. 列车准点节能运行的控制工况最优切换研究[J]. 中国铁道科学, 2016, 37(2): 91−98. WANG Qingyuan, FENG Xiaoyuan. Optimal switching for control conditions of punctual and energy efficient operation of train[J]. China Railway Science, 2016, 37(2): 91−98.
[12] LI L, DONG W, JI Y D, et al. Minimal-energy driving strategy for high-speed electric train with hybrid system model[J]. IEEE Trans Intell Transp Syst, 2013, 14(4): 1642−1653.
[13] 吴洋, 罗霞. 一种晚点地铁列车实时调整策略及其动态调控模式[J]. 中国铁道科学, 2005, 26(6): 113−118. WU Yang, LUO Xia. Tactic for real-time operation adjustment and corresponding dynamic velocity control mode for delayed metro trains[J]. China Railway Science, 2005, 26(6): 113−118.
[14] Wong K K, Ho T K. Dwell-time and run-time control for DC mass rapid transit railways[J]. IET Electr Power Appl, 2007, 1(6): 956−966.
[15] 黄友能, 宫少丰, 曹源, 等. 基于粒子群算法的城轨列车节能驾驶优化模型[J]. 交通运输工程学报, 2016, 16(2): 118−124. HUANG Youneng, GONG Shaofeng, CAO Yuan, et al. Optimization model of energy-efficient driving for train in urban rail transit based on particle swarm algorithm[J]. Journal of Traffic and Transportation Engineering, 2016, 16(2): 118−124.
[16] YANG X, NING B, LI X, et al. A two-objective timetable optimization model in subway system[J]. IEEE Trans Intell Transp Syst, 2014, 15(5): 1913−1921.
[17] Kennedy J, Eberhart R. Particle Swarm optimization[C]// Proc IEEE Int Conf Neural Netw, Perth, Australia, 1995: 1942−1948.
On energy-efficient operation for high-speed trains by particle swarm optimization
HE Zhiyu1, 2, YANG Zhijie2, LÜ Jingyang3, CHEN Huiyuan2
(1. Postgraduate School, China Academy of Railway Sciences, Beijing 100081, China; 2. Signal & Communication Research Institute, China Academy of Railway Sciences, Beijing 100081, China; 3. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China)
In order to solve the problem of energy-efficient operation between multiple stations for high-speed trains, this paper investigates the allocation strategy of redundant time based on timetable optimization. According to train dynamic model and energy-efficient operation strategy, we proposed an optimization model aiming at punctuality and energy consumption. Then, Particle Swarm Algorithm was applied to allocate the redundant time reasonably and search the optimal solution iteratively based on the fitness value. According to the real geographical data of Beijing-Shenyang high-speed railway, we simulated the profiles of speed—distance and energy consumption—distance. Comparing to other allocation strategy of redundant time, the proposed algorithm can reduce the total energy consumption by ensuring the punctuality. The effectiveness of the proposed algorithm was verified. And it provides a reference for the train working diagram.
railway transportation; redundant time; energy-efficient operation; particle swarm algorithm
U268.6
A
1672 − 7029(2019)07− 1622 − 06
10.19713/j.cnki.43−1423/u.2019.07.003
2018−09−30
中国铁路总公司科技研究开发计划课题(2017X002,2018G009)
杨志杰(1961−),男,云南大理人,研究员,从事高速列车运行控制的研究;E−mail:natureyang@sina.com
(编辑 阳丽霞)
