十字轴万向节用滚针轴承承载问题研究
2019-03-23宗晓明高飞韩红雨
宗晓明 高飞 韩红雨
一、引言
十字轴式万向节是汽车传动系统中的关键部件,起着传递发动机输出动力的作用,其优劣直接影响整车的平稳性、经济性。十字轴与轴叉、节叉之间采用双列滚针轴承进行支撑连接,滚针轴承内部载荷和应力分布是影响轴承甚至十字轴总成性能和寿命的重要因素。
而随着计算机仿真分析技术的发展,对十字轴静力学、运动学的分析研究也陆续开展。张向阳等人对十字轴进行了模拟分析,以降低轴颈处的最大应力为目标,对其结构进行了优化。朱福先等人采用ANSYS软件对十字轴的轴向和环向接触压力进行了仿真分析研究,得出十字轴轴向和环向接触压力的分布规律。汪利霞等人对十字在扭炬载荷下的应力进行了分析。J.Eddie等人建立了双十字轴万向节联轴器输入轴和输出轴之间的运动方程式,为一般万向节的运动分析研究提供了参考依据。以往的研究多针对万向节总成,尚未见针对其承载滚针轴承的研究。
本文对十字轴万向节用滚针轴承的承载问题进行了分析研究,对轴承内部载荷分布进行了分析,通过建立接触有限元模型,分析最大受载滚针与十字轴颈的接触应力特征,并对结构参数对承载的影响规律进行分析,为十字万向节的工程应用提供理论支持。
二、十字轴万向节用滚针轴承工况的特殊性
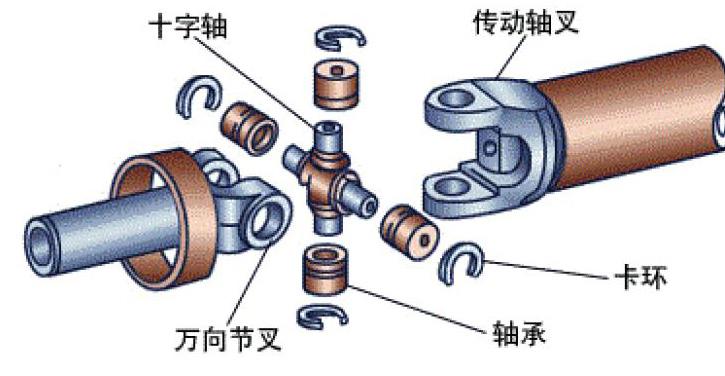
十字轴万向节的结构示意图如图1所示,十字轴万向节主要由传动轴叉、十字轴、轴承、卡环和万向节叉部分组成,滚针轴承安装于十字轴与轴叉、节插之间,起传递载荷与扭炬的作用。与普通滚针轴承相比,万向节十字轴滚针轴承的工況具有特殊性,主要存在如下差异:
当传递扭炬时,轴承内圈与外圈相对产生偏转而非径向位移。这就导致两列滚针实际工作游隙不相同,十字轴端部滚针承受载荷大于轴颈根部的滚针。
由于滚针轴承承受载荷为重载,十字轴弯曲变形尺度与径向游隙接近同量级,这也会引起两列滚针承载变化,按照刚性套圈假设易引起较大误差。
考虑径向游隙导致的内外圈相对倾斜、套圈变形及滚针凸度的影响,滚针与十字轴、外圈接触应力分布也和经典Hertz假设发生了较大的变化。
三、十字万向节滚针轴承载荷分布研究
1、轴承载荷及寿命分析原理简介
假设轴承径向游隙为Pd,则受载前每个滚动体与滚道间法向间隙为Pd/2。受到径向载荷Fr之后,轴承内、外圈沿载荷作用方向发生相对位移δr,位于外载作用线下方的滚动体受载最大,其接觸变形为:
可得轴承内部载荷分布结果。
对双列或多列轴承,根据标准GB/T 6391-2010《滚动轴承额定动载荷和额定寿命》,在载荷计算时在滚动体长度L前添加列数i即可,即假定两列滚动体的承载情況相同。
本研究中,十字轴万向节用滚针轴承的基本参数见表1所列。
2、考虑径向游隙及倾斜影响的载荷分布计算
在输入转炬作用下,十字轴相对套圈有相对旋转的运动,且由于径向游隙的原因导致相互之间形成一定倾角α,如图2所示,并进而导致两列滚针径向间隙的不同,引起两列滚针载荷分布出现差异。
根据上述原因,结合轴承载荷计算方法,由轴承径向游隙计算出倾角α值,再计算十字轴倾斜后两列滚针分别的径向间隙,计算流程如图3所示。
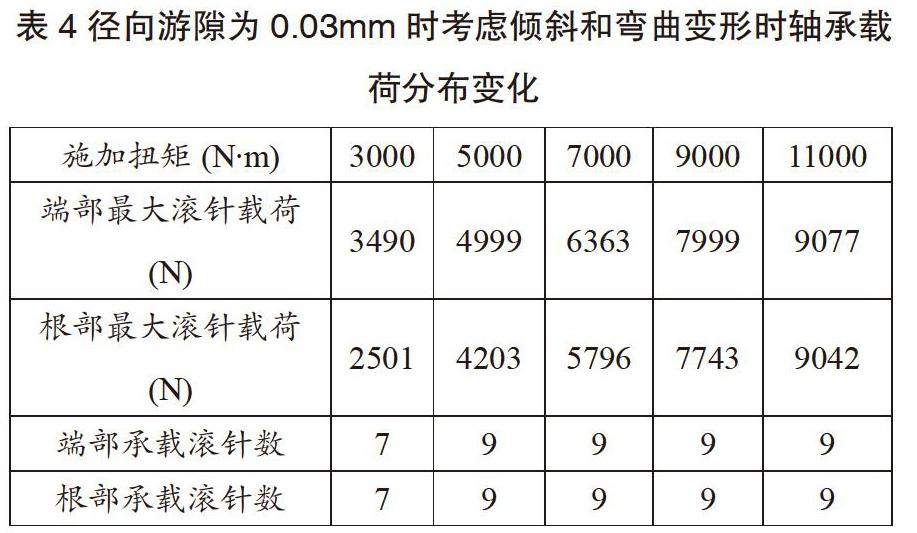
采用上述计算程序再次计算径向游隙为0.03mm、扭炬为3000-11000N·m时滚针轴承内部载荷分布,结果如表2所列。由表2可知,随扭炬的增大,端部最大滚针载荷和根部最大滚着载荷均呈增大趋势,且端部载荷大于根部载荷。
对径向游隙分別为0.03、0.06、0.09,扭炬为11000N·m作用下轴承载荷分布进行计算,所得结果如表3所列。由表3可知,随径向游缝的增大,端部最大载荷增大明显。这是由于考虑倾斜后,端部载荷作用方向的滚针部位径向游隙最小,导致接触作用时其法向变形最大,承受的分布载荷也最大。另外,由于两列滚针的径向游隙不再相等,承受载荷的滚针数量也有所区别;初始径向游隙越大,初始倾角也越大,最大滚针分布载荷变化也越明显。
3、考虑径向游隙、倾斜及十字轴弯曲变形影响的载荷分布计算
十字轴在受力后近根部的变形很小,而接近端部的变形较大,与悬臂梁相似,如图4所示。在后续十字轴弯曲变形计算中也采用材料力学关于悬臂梁的计算方法,具体方法为:
假设十字轴根部为约束位置,即忽略十字轴中段部分的变形,仅考虑轴承滚道部分的弯曲变形。
假设滚针对十字轴的接触载荷为滚针中间位置的集中载荷。
各滚针径向作用力产生的力炬矢量和等于十字轴传递扭炬的1/2。
各滚针载荷导致的十字轴弯曲变形之矢量和为最终的十字轴弯曲变形。
根据材料力学一维梁单元的弯曲变形原理,一维悬臂梁径向弯曲变形计算方程为:
式中L为悬臂梁全长,x为悬臂梁的长度方向坐标,w为x位置的竖直方向变形,F为竖直方向作用载荷,a为载荷F作用点坐标,E为悬臂梁的弹性模量,I为载荷作用方向的惯性炬,对圆柱形结构而言,I的计算公式为:根据上述原理所得计算方法和计算流程如图5所示。采用图5所述计算程序计算径向游隙为0.03mm、扭炬为3000-11000Nm时滚针轴承内部载荷分布,结果如表4所列。由表4可知,综合考虑了十字轴与外圈相对倾斜及十字轴弯曲变形的影响后,载荷较表2中计算获得的数值相比有明显减小,这是由于径向游隙产生的轴承内、外滚道倾斜虽然导致了载荷分布的差异,但十字轴弯曲变形在一定程度上弱化了倾斜所造成的影响,并且随着载荷的增大,两列滚针的载荷分布有接近的趋势。由于并未考虑外圈的变形影响,因此上述结果与实际情况在趋势性上应该还有一定的差异。
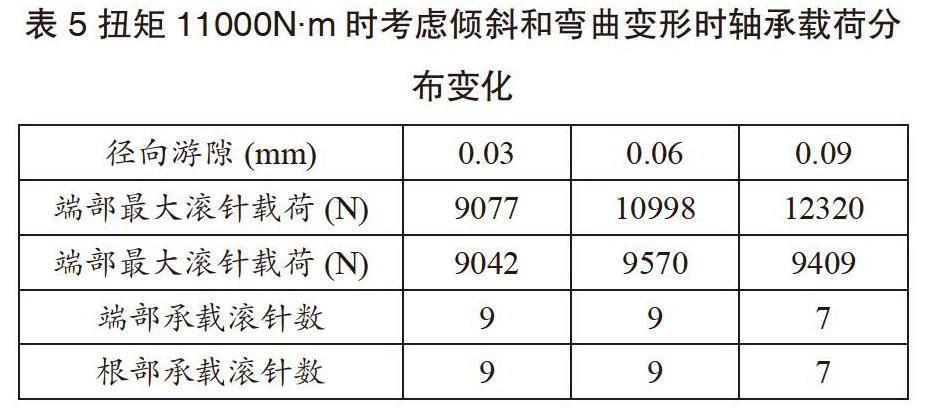
在11000N·m载荷条件下,不同径向游隙状态时的载荷分布结果如表5所列。由表5可知,综合考虑了十字轴与外圈相对倾斜及十字轴弯曲变形的影响后,载荷较表3中计算获得的数值相比有明显减小,其原因同样是由于十字轴弯曲弱化了倾斜带来的载荷分布不均影响,这从两列滚针中承载滚针数量的变化也可以体现出来。
由以上分析可知,由于径向游隙导致的十字轴与外圈之间的相对倾斜,以及十字轴的弯曲变形对滚针轴承内部载荷分布有明显的影响。相对倾斜导致两列滚针最大载荷分布出现较大偏差,而十字轴的彎曲变形则在一定程度上减小了载荷的差值。径向游隙对载荷分布的影响较大,在载荷计算中应考虑其影响。随着径向游隙的增大,两列滚针的载荷分布最大值之差有增大趋势。综上原因,在后续应力计算过程中,将采用第三种载荷分布计算方法所得结果作为应力分析的输入条件。
4、滚针接触应力模拟分析
通过上述计算可以发现,在径向游隙为0.03~0.09mm情况下,十字轴端部承载方向滚针承受最大分布载荷。根据轴承疲劳寿命原理,在转速不是很高的条件下,最大承载滚动体与内圈的接触应力分布,尤其是其接触应力极值是关注的重点。因此,采用ANSYS软件建立十字轴——单个滚针——局部外圈接触模型来分析滚针接触特性,并探索径向游隙、凸度对接触应力极值的影响规律,接触模型材料参数的设置情况如表6所列。
根据前述分析,对十字轴——滚针——局部外圈模型提出如下假设:
外圈外表面设置为完全刚性面。
十字轴中间部位假设为完全刚性,无弹性变形。
每粒滚针与十字轴的接触变形对邻近滚针接触无影响。
根据万向节结构图样建立几何模型如图6所示,其中十字轴与端部接触滚针均为1/2对称模型。根据工况和分析假设,对模型施加如下位移约束和载荷条件:
对模型对称面施加对称约束。
根据十字轴中间部位变形量远小于端部的情况,在根部截面施加全方向的位移约束。
设置外圈外表面为刚性面,并设定表面所有节点在外载作用下的径向位移相等。
在滚针表面与外圈内表面、十字轴外径面设置接触对,设摩擦系数为0.1以约束滚针的位移。
在外圈外表面施加竖直向下的载荷,载荷大小根据第三种载荷分布计算方法所得最大滚针分布载荷确定。
采用上述模型对滚针凸度为0.005μm,径向游隙0.03mm,传递扭炬为11000N·m工况下的应力分布进行了计算,此时十字轴端部滚针承受径向载荷值为9077N。图7为该载荷作用下滚针与十字轴接触应力云图。接触应力沿轴向的分布区域呈近似狭长带状,最大接触应力为3907.88MPa,如图7所示。
作为对比,采用经典方法对9077N载荷作用下的接触应力极值进行计算,有
有限元计算的结果要明显高于理想线接触计算值。将图7中对称线上节点所受接触应力值绘制成曲线,得图8。从图8中可以看出,两计算方法结果偏差主要是由于应力沿轴向并非理想线性分布所致,在滚针两端存在应力峰值。由于十字轴与外圈间存在一定倾斜,曲线主要承载段显示出一定的角度。
对3000N·m、7000N·m和11000N·m载荷时的应力分布分別计算,其轴向接触应力曲线如图9所示,应力极值随载荷变化的曲线如图10所示。从图10中可以看出,应力极值随外加扭炬的增大而逐渐增大,但斜率逐渐放缓。
轴承径向游隙会导致最大滚针载荷发生变化,也导致十字轴与外圈发生相对倾斜,进而影响接触应力的大小。为分析径向游隙的影响,对径向游隙为0.03mm、0.06mm和0.09mm时,11000N·m扭炬载荷作用下最大承载滚针的接触应力极值进行了计算,结果如表7所列。不同径向游隙对应接触应力分布曲线如图11所示。
由表7可知,轴承径向游隙的变化对接触应力的影响十分显著,当轴承取最大径向游隙0.09mm时,其接触应力极大值比0.03mm径向游隙时增大了约13.2%。因此,在载荷较大时应尽量选取小的径向游隙值以避免产生过大的接触应力,导致轴承产生早期失效。
四、结论
针对十字轴万向节用滚针轴承的工况特点,本研究提出了两种计算滚针轴承内部载荷分布的计算方法,并采用MATLAB编程对扭炬作用下万向节十字轴滚针轴承内部载荷分布进行了计算分析,通过ANSYS软件对滚针与十字轴接触应力进行了计算,得如下结论:
在考虑径向游隙及倾斜影响的条件下,随扭炬载荷的增大,端部最大滚针载荷和根部最大滚着载荷均呈增大趋势,且端部载荷大于根部载荷;隨径向游缝的增大,端部最大载荷增大明显。这是由于考虑倾斜后,端部载荷作用方向的滚针部位径向游隙最小,导致接触作用时其法向变形最大的原因。
在考虑径向游隙、倾斜及十字轴弯曲变形影响的条件下,随扭炬载荷的增大,端部最大滚针载荷和根部最大滚着载荷均呈增大趋势,且考虑了十字轴变形影响因素后,载荷值较仅考虑径向游戏及倾斜变形时小,主要是由于十字轴弯曲变形在一定程度上弱化了倾斜所造成的影响,并且随着载荷的增大,两列滚针的载荷分布有接近的趋势。
有限元分解结果表明,径向游隙是影响轴承内部载荷及应力分布的主要因素,应尽可能选取较小的径向游隙范围以避免滚针承载过大、应力极值过大导致的轴承失效。
