基于改进遗传算法的多模式气温集成预报方法研究
2019-03-23游枭雄刘二影
游枭雄 戴 劲 何 宁 刘二影
(湘潭市气象局,湖南 湘潭 411100)
随着数值预报业务技术的迅速发展,数值产品的准确度和分辨率也得到了极大的提高,面对不断增长的海量数值预报产品,如何在短时间内有效地对其进行利用成为目前天气预报业务中面临的主要问题之一,从而促使了多模式集成预报方法研究的快速发展。目前主要的集成预报方法有多元回归集成法、权重分布法、神经网络集成法等[1-4]。近年来也有学者尝试利用遗传算法(GA)开展气温集成预报实验[5],这类方法在试验中都表现出较高的预报精度,但也存在着一些问题:运算时间过长、计算结果不够稳定等[5]。
本文将针对遗传算法的缺点进行改进,利用EC细网格、日本细网格和德国模式48 h内预报数据进行逐6 h气温预报实验,并对算法的预报性能进行对比分析。
1 遗传算法
1.1 遗传算法简介
遗传算法[6](GA)是一种模拟生物进化规律的全局搜索算法,它的主要目标对种群个体优胜劣汰并使其得到进化,通过多次的进化获得更好的结果。标准的遗传算法包含选择、交叉、变异三个基本步骤,每完成一次运算即对个体完成一次进化,在经过多次进化后得出最优解。遗传算法具有全局搜索能力强、收敛性好的特点,但也存在早熟、计算时间长、稳定性差的缺点。
1.2 改进遗传算法
自标准遗传算法被提出以来,众多学者一直致力于推动遗传算法的发展,不断地提高遗传算法的性能[7-9],经过对比分析,文献[9]中的精英个体保留策略对算法性能提升的影响较大,其在进化过程中保留父代和交叉所得新个体中的优秀个体,从而保证在进化过程中不会丢失最优解,由于精英个体得以保留,可将交叉概率设为1,能极大提高全局搜索效率,本文将引入该策略对遗传算法进行优化。
改进后的算法步骤为:①首先产生初始种群,种群规模为n;②计算每一个个体的适应度;③按照轮盘赌选择法选择个体进入下一代;④对选择的个体进行交叉;⑤对交叉产生的n个个体和n个父代个体按适应度排序,保留前m个精英个体;⑥对交叉产生的n个个体,按概率Pm进行变异;⑦用m个精英个体替换变异后种群中m个最差个体;⑧若满足求解条件则终止进化进入下一步,若不满足则转至第②步;⑨输出种群中最优解。
算法流程图如图1所示。
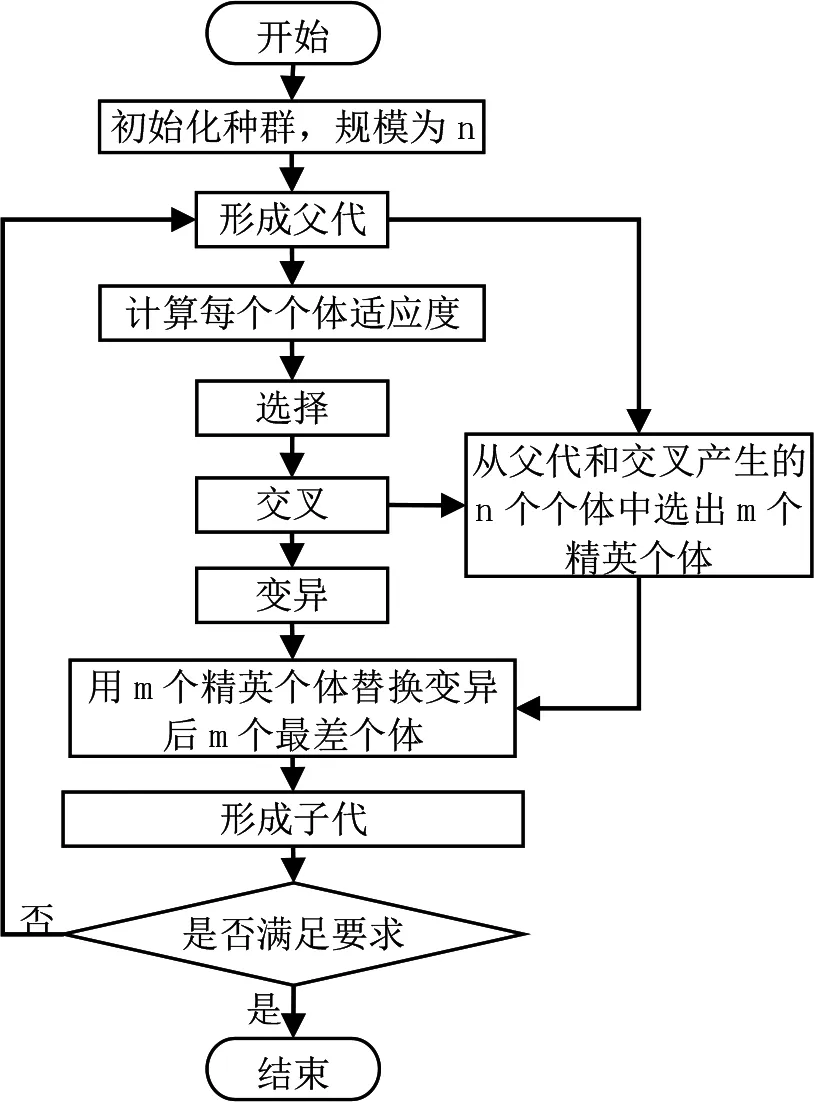
图1 改进遗传算法流程图
2 改进遗传算法气温集成预报
2.1 集成方法
本文采用权重系数分配法对多个模式预报值进行集成,而各模式的权重系数以及偏差则由改进的遗传算法计算得出,对于单一站点,如式(1)所示。
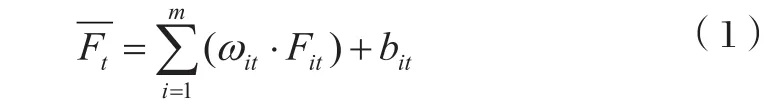
式中: i—预报模式; t—时次; m—预报模式个数;Fit—模式预报值;ωit—权重系数;bit—偏差;—集成预报值。
2.2 算法设计
改进遗传算法的具体步骤包含:编码方式、超参数设定、适应度函数、选择操作、交叉操作和变异操作,根据本文的改进策略还涉及精英个体保留操作,具体设计如下:
(1)编码方式:采用实数编码,所有个初始化为(-1,1)的实数。
(2)超参数设置:超参数即为算法开始学习前需提前设置的参数,本算法中需要设置的超参数有种群规模、迭代次数、保留精英个体数、交叉概率Pc、变异概率Pm,由于本文采用精英保留策略,因此,可将交叉概率Pc设为1,以增大全局搜索能力,变异概率Pm设为0.05,其他参数则根据训练样本酌情设置。
(3)适应度函数:用于评价个体的好坏,本文适应度函数设计如式(2)所示:

(4)选择操作:本文采用轮盘赌选择法[6],适应度越高则被选择几率越大。
(5)交叉操作:根据实数编码的特点,本文采用一致交叉法进行算术交叉,先随机选取两个父代 和 ,经过交叉后得到新个体 和 ,具体公式如下:
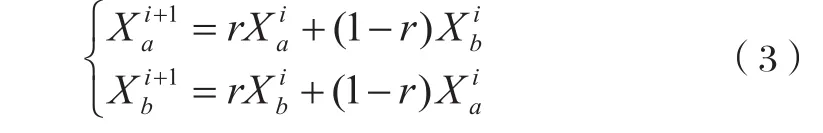
式中:r—(0,1)间随机数。
(6)变异操作:遍历群体中所有个体和基因,对于每个基因产生一个随机数P和变异概率Pm比较,若P小于Pm则生成一个(0,1)间的随机数替换原基因。
(7)精英个体保留操作:将交叉产生的新群体和父代群体组合起来按适应度排序,保留前m个精英个体,变异之后再用m个精英个体替换变异后种群中较差的m个个体,形成子代。
3 预报实验
3.1 数据资料及预处理
(1)数值预报产品资料。EC_thin、JAPAN、GERMAN三个模式2 m高度气温预报格点插值产品,区域为湘潭国家站点位置,时间范围为2016年10月1日~2018年12月10日,起报时间为每日8:00和20:00,考虑实际工作中0~6 h内预报数据没有实际使用价值,因此,仅采用12~48 h内逐6 h预报值作为实验数。
(2)实况资料。湘潭国家观测站的2:00、8:00、14:00、20:00逐日气温资料,时间范围为2016年10月1日~2018年12月12日。
(3)预处理。将数值产品按时间顺序取最晚的20%作为测试数据集,剩下的作为训练集,所有数据均去除漏报和无效值。
3.2 实验分析
设定初始化种群规模为60,保留精英个体数为10,迭代次数为300次。由于数值产品在不同起报时间和预报时次上精度差异较大,因此,采用按起报时间和预报时次单独建立预报模型的方式进行实验,并将改进遗传算法与基本遗传算法以及各模式产品的预报性能进行比较,检验指标包括平均绝对误差和绝对误差小于2 ℃的准确率。
经实验,改进遗传算法与标准遗传算法及三种模式的在各时次的预报准确度和平均绝对误差如图2所示,在各时次的预报准确率与平均绝对误差上改进遗传算法明显优于标准遗传算法以及三个模式。将各时次的准确度与平均绝对误差取平均,结果如表1所示,改进遗传算法相对标准遗传算法有明显的提升,其中,准确度8:00起报提高了2%,20:00起报提高了4%,平均绝对误差也降低了0.1~0.2 ℃。
将迭代次数设为500,检验改进遗传算法与标准遗传算法的运算效率,结果如图3所示,改进遗传算法收敛速度比标准遗传算法更快,精度更高。
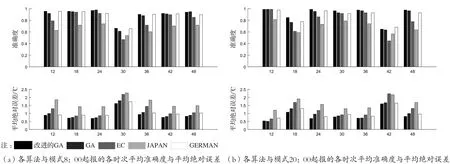
图2 各时次准确度与平均绝对误差

表1 各算法与各模式所有时次平均准确度与平均绝对误差
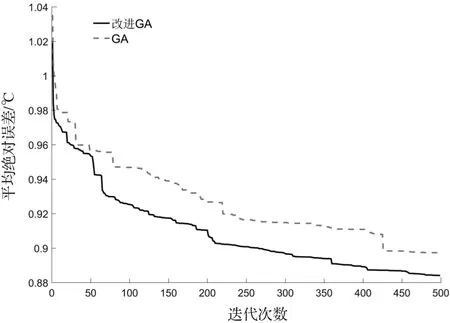
图3 两种算法平均绝对误差随迭代次数的变化
通过对比分析可见,基于改进遗传算法的集成预报明显优于其他模式预报结果,且性能相对于标准遗传算法显著提高。
4 结语
改进的遗传算法通过加入保留精英个体策略,加快了算法的收敛速度,且大大提高了算法的精度,相对于标准遗传算法的缺陷有了明显的改善。通过实验可以看出,基于改进遗传算法的多模式气温集成预报结果明显优于各模式预报值,在实际的预报工作中具有较高的参考价值。
