基于计算流体方法对建筑物风场分布*

芦红莉

(天津科技大学 艺术设计学院， 天津 300450)

随着现代建筑外形越来越复杂，高度越来越高，建筑风场的研究逐渐得到各方的关注[1].其研究手段包括现场实测、实验室模拟(主要是风洞模拟)和理论分析(包括数值计算)[2].现场实测作为对其他两种研究手段模拟结果的检测是必不可少的，也是最直接的研究手段，但其成本高、时间长且不易测量，只有在建成后才可以测量，无法为拟建建筑提供预测，因此具有一定的局限性[3].风洞试验作为一种实验室模拟手段，应用较为广泛，对于体型复杂的建筑物，如大跨度体育场屋盖结构，或高层建筑，都宜进行风洞试验.风洞试验能够得出相关结果，并验证新方法的有效性.通过建立物理模型能够研究一些具体位置的风场，从而检测各种假设.风洞的缺陷是其具有稀缺性，尤其是用于研究城市的模型，风洞需要足够大，且在模型中的测点是有限的[4].

近年来，计算流体动力学(CFD)在建筑物风场的研究中得到了越来越多的应用，已有研究用该方法从定性和定量方面较准确地预测了风场的影响[5].与前两种手段相比，其人力和物力的消耗小，且能够对研究对象整体进行定量和定性分析，而不仅是仪器测量的几个点.但是，需要证明计算结果的正确性和可行性，尤其是建筑物周围风场涉及到复杂的湍流流动[6].因此，利用CFD方法研究风场模型的准确性验证需要更深入的研究.

本文介绍了使用FLUENT计算结果与风洞试验结果进行对比验证所建立的CFD模型方法，并优化了模型参数，为今后城市风场的研究提供一定的依据.

1 基本原理

CFD是利用高速计算机求解流体流动的偏微分方程组，目的是为了更好定性和定量地了解流体流动的物理现象.CFD计算包括前处理、求解和后处理三部分[7-8].FLUENT是常见的CFD软件之一，其本身所带的物理模型可以准确地预测层流、过渡流和湍流多种复杂现象.其中湍流模型理论(简称湍流模型)，就是以雷诺平均运动方程与脉动运动方程为基础，依照理论与经验的结合，引进一系列模型假设，而建立起的一组描写湍流平均量的封闭方程组.本文选取FLUENT软件提供的k-ε模型，雷诺应力模型(RSM)即可实现k-ε模型进行计算分析.

k-ε模型自从被提出就成为工程流场计算中的主要工具，其湍动能输运方程是通过精确的方程推导得到的，耗散率方程是通过物理推理，数学上模拟相似原型方程得到的[9].可实现的k-ε模型是近期才出现的，比起标准k-ε模型有两个主要的不同点：1)为湍流粘性增加了一个公式；2)为耗散率增加了新的传输方程，这个方程来源于一个为层流速度波动而做的精确方程[10].RSM在FLUENT中是最精细的模型.放弃等方性边界速度假设，使雷诺平均N-S方程封闭，解决了关于方程中的雷诺压力，还有耗散速率.这意味着在二维流动中加入了四个方程，而在三维流动中加入了七个方程[11].由于RSM比单方程和双方程模型更加严格地考虑了流线型弯曲、漩涡、旋转和张力快速变化，对复杂流动有更高的精度预测潜力.

2 建立数值模型

2.1 物理模型

本文模拟计算了单一建筑，两栋建筑和城市建筑群的风场分布.图1为单一建筑模型参数，建筑长80 m，宽12 m，高18 m，中间为通道，宽6 m，高4 m.

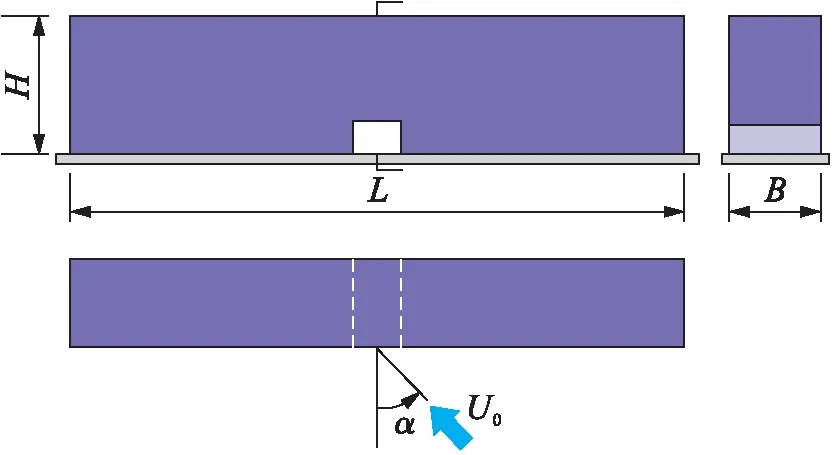
图1 单一建筑模型参数Fig.1 Model parameters for single building

图2为两栋建筑的分布图，两栋建筑高为18 m，中间通道宽b为4 m，风向如图2所示.

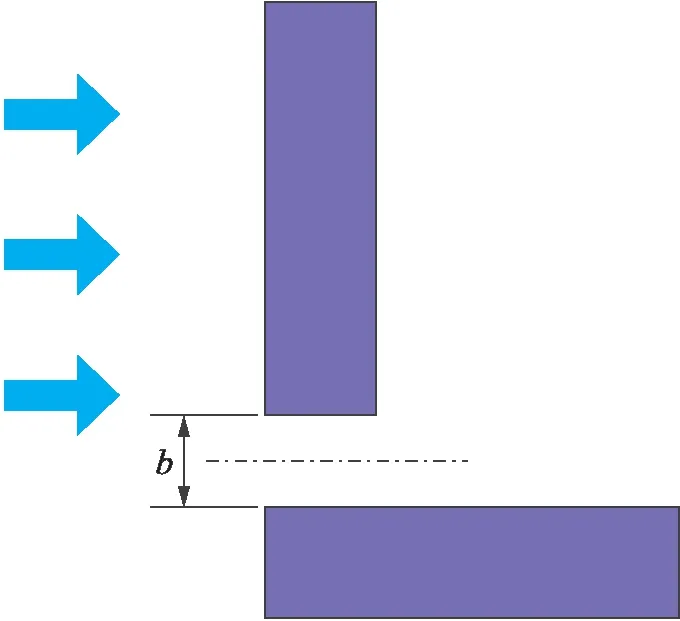
图2 两栋建筑模型参数Fig.2 Model parameters for two buildings

图3为城市中复杂建筑群分布图，图4为风洞试验中各种测量点的位置[12].模型为不同高度的建筑群，中央建筑高度(76 m)为周围建筑高度的四倍(19 m)，街道宽度为25 m.

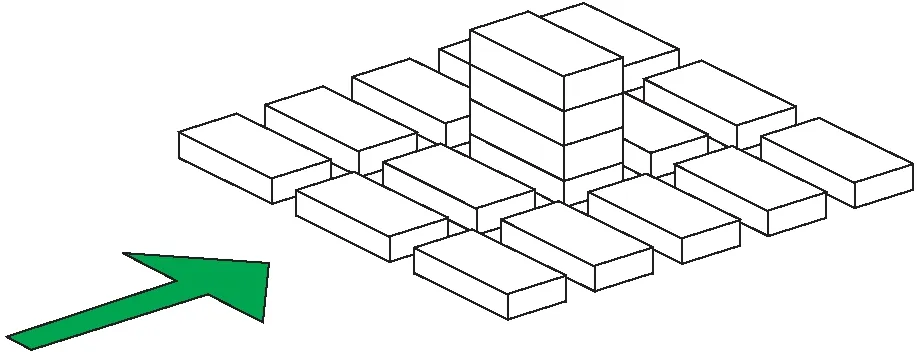
图3 城市综合体结构图Fig.3 Structure of urban complex

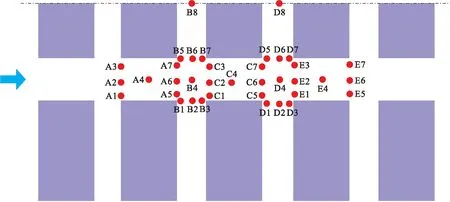
图4 风洞试验测点Fig.4 Measurement points in wind tunnel test

所建立模型需要满足以下条件：1)阻塞率不应超过3%；2)模型截面(宽度×高度)形状应优先遵循暴露于风中的建筑物表面的形状；3)模型长度在建筑物的上游延伸量大于10H，下游延伸量大于16H，H为较高建筑物的高度；4)满足对称条件，模拟一半模型的风场.

2.2 边界条件

模型边界和上表面对称，风入口处设为VELOCITY-INLET，风离开模型的表面设为OUTFLOW，其余边界设为WALL，假设地面和建筑物表面光滑(即粗糙度为0)，墙体附近采用近壁面函数.

3 结果分析

3.1 单个建筑风场数值计算

图5为单个建筑(80 m×12 m×18 m)的模拟结果，通过FLUENT软件计算各种湍流模型的U/U0值，并与Wiren的风洞试验结果进行比较[13].其中，U/U0为有建筑物时2 m处的风速与无建筑物时相同高度风速的比值[13].

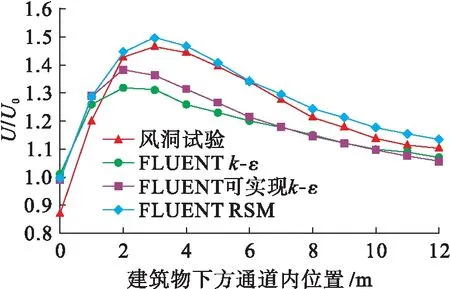
图5 不同FLUENT湍流模型计算结果与风洞试验对比Fig.5 Comparison between calculated results of differentFLUENT turbulence models and wind tunnel test

由图5可知，雷诺应力模型(RSM)模拟结果与风洞试验结果吻合最好，可用于评估单个建筑物通道中行人对风的舒适度.该湍流模型不仅能识别关键区域，而且可以准确地确定最关键位置和风的最大不适值.因此，RSM湍流模型能够应用于建筑物风力舒适性的研究.

3.2 两栋建筑物风场数值计算

通过单个建筑的研究得出，RSM湍流模型与风洞试验吻合结果最好，因此，两建筑计算模型采用RSM湍流模型与风洞试验进行对比.图6为FLUENT RSM湍流模型计算结果与风洞试验对比.两栋楼通道风速强度与Wiren风洞测试结果[13]吻合，与风洞试验的测量值误差小于等于10%，因此，FLUENT软件的RSM湍流模型可用于预测建筑物风场的研究，以确定行人的舒适性和最大风速值.

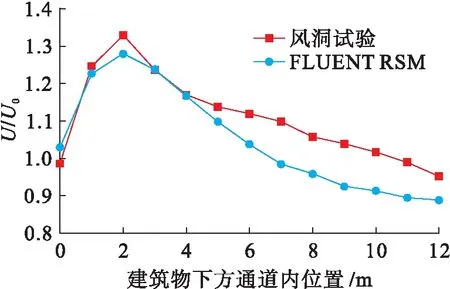
图6 FLUENT RSM湍流模型计算结果与风洞试验对比

Fig.6ComparisonbetweencalculatedresultsofdifferentFLUENTRSMturbulencemodelsandwindtunneltest

通过以上分析得出，FLUENT是评估建筑物风场影响的有效工具.FLUENT定性和定量两方面评估两座建筑物周围的风速.RSM模型是研究小群建筑物风力的理想湍流模型.

3.3 城市建筑群风场数值计算

图7为FLUENT各模型对各街区U/U0比值平均值的计算结果，与Stathopoulos & Wu风洞试验[12]进行对比，并选取风洞试验风速为8 m/s.五个街区点组为：A1～A7，B1～B8，C1～C7，D1～D8，E1～E7.

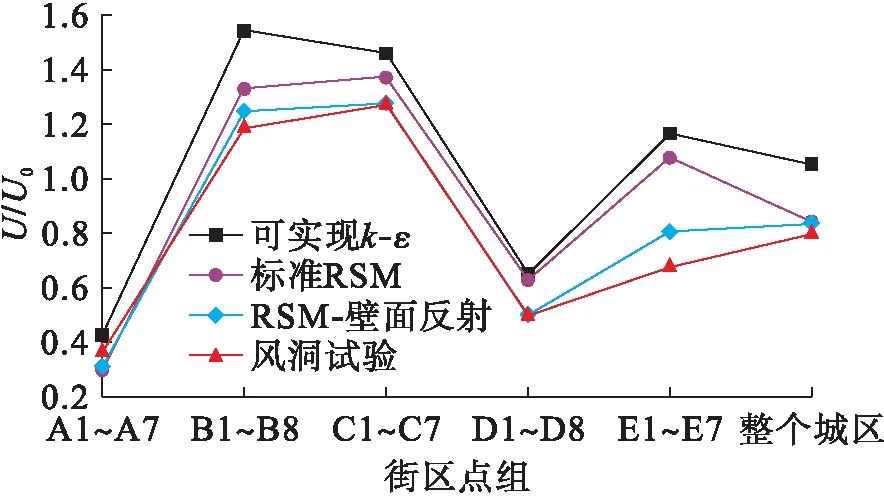
图72m高度处不同FLUENT湍流模型计算结果与风洞试验对比

Fig.7ComparisonbetweencalculatedresultsofdifferentFLUENTturbulencemodelsandwindtunneltestatheightof2m

标准k-ε模型计算结果与试验结果偏差最大，标准RSM模型所计算的整个城市地区的平均值与风洞试验结果接近，相对误差为5%.而RSM-壁面反射模型精度更高，五个街区和整个城区的计算结果都与风洞试验测量值吻合较好.因此，RSM湍流模型结合壁面反射适用于研究密集城区建筑物风场，并可用于研究不同高度的建筑群.

图8为中间三排风速变化较大的九栋建筑物2 m高处水平面风速分布图，图9为垂直面的速度分布图.

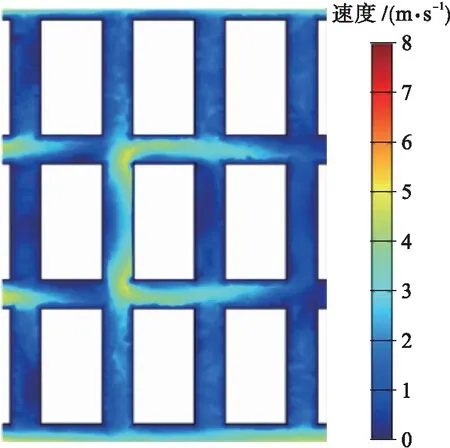
图8 高度2 m处水平面风速分布Fig.8 Wind speed distribution in horizontalplane at height of 2 m

通过以上分析，城区中具有不均匀高度的建筑群可采用RSM-壁面反射模型进行计算.但本文方法可以预测几区或者整个城区的平均风速，无法确定每个点上的精确风速，能够预测最高风速的区域，但是准确位置可能会局部偏移.

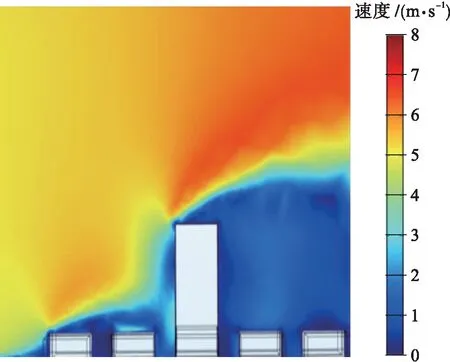
图9 通过B8和D8的垂直面风速分布Fig.9 Wind speed distribution in verticalplane through B8 and D8

然而，实际应用中并不需要特定点的确切风速，只需要知道防风区，即给行人带来不舒适性的区域.因此，本文模型能够评估风的不舒适区域，以辅助建筑师或城市规划师设计出舒适的公共空间.

4 结 论

本文建立了建筑物风场模型，并验证了模型的正确性.通过研究发现，从定性的角度来看，FLUENT提出的RANs湍流模型能够计算单个建筑物或小群建筑物以及城区非均匀高度建筑群的平均风速.从定量角度考量，RSM湍流模型更加适用于研究建筑物的风场，较好地预测三类建筑的平均风速分布.所建立的模型能够识别关键区域并量化风的不适程度.对于单一建筑和小群建筑，标准RSM模型计算结果最好.在城区建筑群的模拟中，RSM-壁面反射模型最好.本文研究为通过模拟计算评估建筑物周围行人的风力舒适性提供依据.