GFRP管混凝土组合构件偏心受压力学性能数值分析*

樊 成， 宋志刚， 宋 力

(大连大学 材料破坏力学数值试验研究中心， 辽宁 大连 116622)

FRP材料作为新兴材料在土木工程的应用中越来越广[1-4]，GFRP管混凝土组合构件的轴心受力状态是其最理想状态，但是在实际应用中由于荷载作用位置的不确定性、施工误差、混凝土的不均匀性等设计、施工的不利因素影响，使得GFRP管混凝土组合构件处于偏心受压状态，而目前对GFRP管混凝土组合结构的偏压研究主要集中在试验研究[5-7]，数值模拟相对比较少，本文利用ABAQUS对大量试件进行数值分析，研究不同因素对构件偏心受力状态的影响，并对GFRP管钢骨混凝土偏心受压承载力公式进行简化.

1 本构模型选择

1.1 混凝土受压本构关系

本文选用与试验吻合度较好的Lam和Teng抛物线加直线本构模型[8]，即

(1)

σc=fc0+E2εc(εt<εc≤εcc)

(2)

(3)

(4)

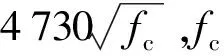
(5)

(6)

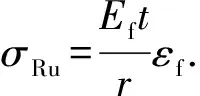
1.2 混凝土受拉本构关系

Gf=10-3a(fc/10)0.7

(7)

式中，Gf为混凝土的断裂能，其物理意义是每单位面积的混凝土产生一条连续裂缝所需要的能量.混凝土受拉软化模型如图1所示，其中，各变量含义见文献[8].

1.3 型钢本构模型

(8)

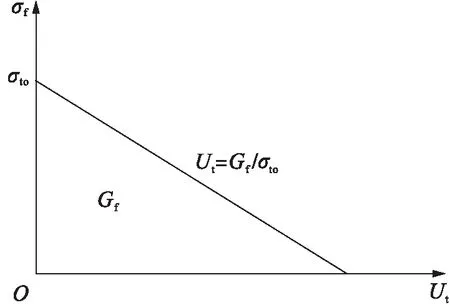
图1 混凝土受拉软化模型Fig.1 Tensile softening model for concrete

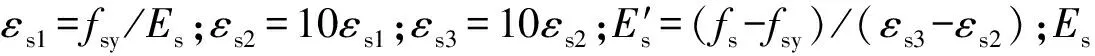
1.4 GFRP管本构模型

GFRP管采用ABAQUS中的单层板模型来模拟其力学性能，ABAQUS定义复合材料的损伤采用Hashin破坏准则[9]，用来近似模拟复合材料的损伤演化过程，单层板的相关参数利用复合材料细观力学中的分析方法，由文献[10]中提供的材料参数计算，并对GFRP管进行铺层设计，铺层设计以3 mm厚角度为80°的GFRP管为例，铺层方式及情况如图2和表1所示，从而完成对GFRP管的定义.

图2 GFRP管铺层方式Fig.2 Layer mode of GFRP tube

单层角度(°)单层厚度mm800.5单层角度(°)单层厚度mm-800.5

2 数值模型的建立与计算

2.1 有限元模型建立

混凝土和GFRP管之间的接触在切向部分采用ABAQUS中自带的库伦摩擦模型，GFRP管与核心混凝土通过粘结作用使得它们之间的相对运动为零，只有两者之间的剪应力达到临界值τcrit时，才产生相对位移，临界剪应力的计算公式为

τcrit=μp

(9)

式中：μ=0.6为摩擦系数；p为GFRP管与核心混凝土之间的接触压力.

混凝土和垫块采用八节点六面体减缩积分单元(C3D8R)，型钢和GFRP管采用四节点减缩积分壳单元(S4R)，厚度方向均采用5个积分点的泊松积分.对钢骨使用Embed命令实现与核心混凝土的作用，GFRP管与端板采用shell to solid coupling命令接触，用tie命令将混凝土与端板进行绑定，端板按照实际偏心距切割加载线，上端板加载线耦合参考点，并在参考点处施加位移荷载，下端板加载线处施加铰接边界条件，网格划分及边界条件如图3所示.

2.2 试验验证

为了验证数值模型的准确性，通过ABAQUS模拟GFRP管中长柱偏压的荷载挠度曲线，本文采用文献[5]中试验数据，详细数据如表2所示(变量含义见文献[5]).

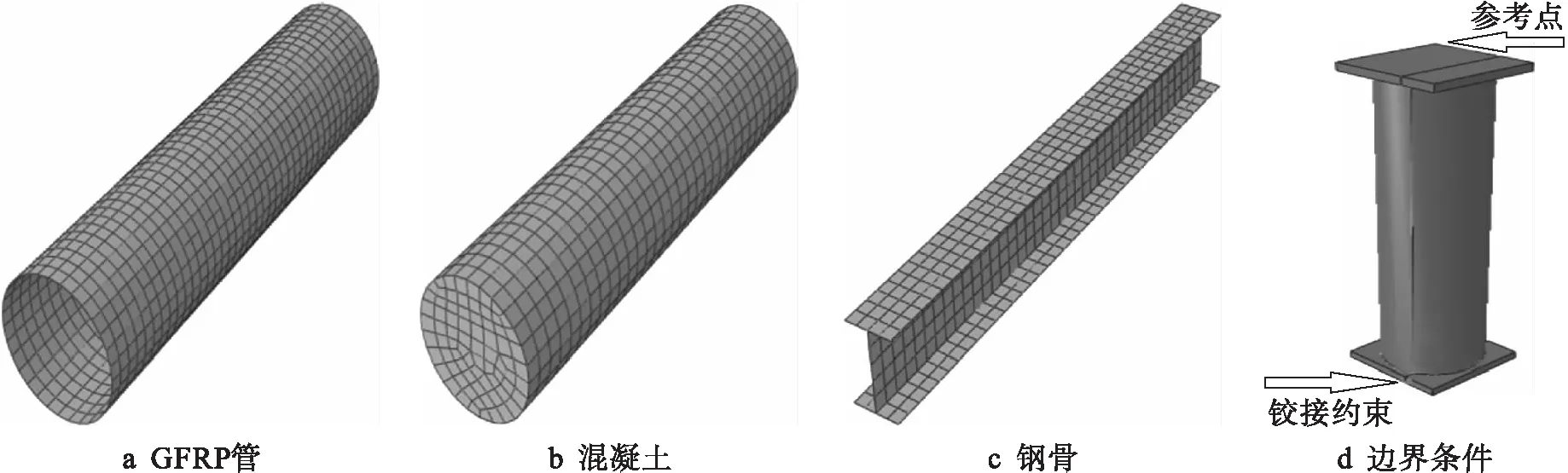
图3 网格划分及边界条件Fig.3 Mesh generation and boundary conditions

编号高度Lmm直径Dmm混凝土强度等级纤维缠绕角度/(°)管壁厚度tmm长细比偏心距NexpkNNcalkNNexpNcalGSPY1800200C708051620249325840.965GSPY2800200C708031620220323230.948GSPY3800200C706051640170017890.950GSPY71450200C708032920204523080.886

通过数值模拟GFRP管约束混凝土偏压柱受力过程，将试验结果与数值模拟计算的荷载N-挠度u曲线进行对比，结果如图4所示，计算结果与试验结果吻合较好，数值模型的准确度可以保证.

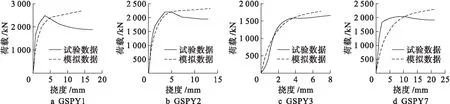
图4 试验与数值模拟N-u曲线对比Fig.4 Comparison in N-u curves between experiment and numerical simulation

3 N-u曲线影响因素分析

GFRP管约束混凝土组合构件偏压力学性能的影响因素有：GFRP管管壁厚度、混凝土强度等级、配骨指标、长细比、偏心距等.为了得到各参数对偏压构件力学行为的影响，设计试件，分别改变各参数，在验证有限元模拟准确性的基础上，模拟以上各参数对N-u曲线产生的影响，结果如图5所示.

1) 混凝土强度的影响.由图5a可知，由于在初始阶段，混凝土未受到GFRP管的约束，组合构件的荷载和挠度呈直线关系，高强混凝土具有抗压强度高、抗变形能力强的特点，随着荷载增加，高强混凝土N-u曲线的斜率趋于平缓，GFRP管的环向约束作用显现，混凝土侧向挠度受到限制，曲线表明，高强混凝土具有较高承载力.

2) 偏心距的影响.由图5b可知，偏心距在荷载作用初期对挠度变形的影响较小，随着偏心距的增大，组合构件稳定性降低，GFRP管对混凝土的约束作用下降，偏心距较大构件的二阶效应增大，挠度增长使其承载力降低.

3) 长细比的影响.由图5c可知，长细比对组合柱的N-u曲线具有显著影响，随着长细比的增大，试件稳定性减小，构件曲线的弹性阶段变短，刚度逐渐丧失；当长细比较大时，组合柱的挠度随荷载的增加而增长较快，组合柱由于失稳承载力下降.

4) 加载方向的影响.由图5d可知，在强轴方向加载时，工字钢受压侧受力面积比弱轴加载时大，当试件偏心距较小时，轴位置距离GFRP管边缘较近，钢骨上下翼缘和GFRP管对混凝土具有较强的双重约束作用；而弱轴方向加载时，由于钢骨的位置与试件形心轴靠近，型钢腹板相比强轴加载时，只有一半协同GFRP管对混凝土起约束作用，此时承载力比强轴加载时下降明显.

5) 钢骨截面形式的影响.由图5e可知，随着钢骨型号改变，钢骨截面积增大，N-u曲线总体趋势相同，随着钢骨截面积增加，构件含钢率增加，增大了构件初期刚度，改善了构件延性，使得组合结构的承载力得到提高.

6) 钢骨强度的影响.由图5f可知，在受力初期，核心混凝土承载，钢骨和GFRP管未参与工作，此时的N-u曲线完全重合，混凝土弹性段过后，钢骨的强度作用开始显现，强度高钢骨承受较高荷载.

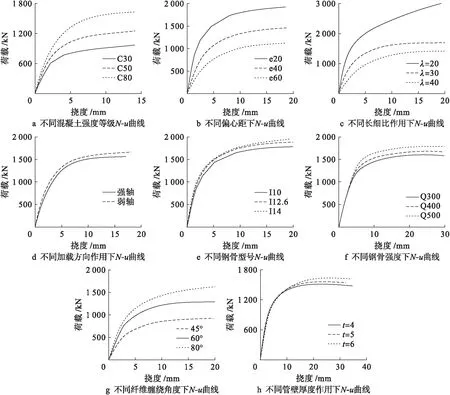
图5 数值模拟N-u曲线Fig.5 N-u curves under numerical simulation

7) 纤维缠绕角度的影响.由图5g可知，在荷载作用初期，由于混凝土受力后侧向膨胀较小，GFRP管的套箍作用不明显，构件变形相差不大，随着挠度增大，较低纤维缠绕角度的环向与混凝土之间的夹角变小，其提供的环向抗拉约束作用降低导致承载力下降.

8) 管壁厚度的影响.由图5h可知，GFRP管在弹性阶段不发挥环向约束作用，此时承载力曲线基本一致，随着弹塑性阶段侧向裂纹的扩展，较厚的GFRP管能够对核心混凝土起到较强的约束作用，有利于承载力提高.

4 偏压柱承载力简化计算

4.1 公式建立

文献[11]基于钢管混凝土的统一理论，给出GFRP管混凝土组合构件偏压承载力计算公式，本文结合钢结构设计规范中关于折减系数的定义，考虑试件长细比影响的承载力简化计算公式为

(10)

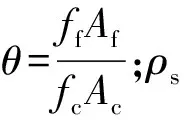
本文基于规范选取λ=16为短柱和长柱的界限值，由于当λ<16时，构件的承载力主要由材料本身强度决定，故本文主要计算受长细比影响较大的λ>16构件，改变构件长细比，承载力与长细比(N-λ)关系曲线如图6所示.

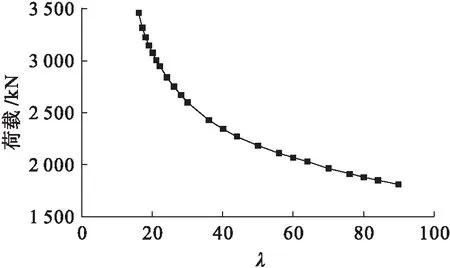
图6 柱的偏压N-λ曲线Fig.6 N-λ curve of column undereccentric compression

由图6可知，偏压柱的承载力随长细比的增加而下降，构件由强度破坏逐渐向失稳破坏转变，当16<λ<21时，承载力变化较快，此时构件主要发生强度破坏，随着长细比逐渐增大，构件极限承载力降低，为此二阶效应的作用也逐渐降低，承载力变化减慢.对有限元计算结果和试验数据进行回归处理，得到柱承载力与长细比有关的折减系数公式为

(11)

式中：L为梁的计算跨度；D为梁的外径.

4.2 公式验证

为了验证公式的准确性，将文献[5，12]中的试验值与计算值进行对比，结果如表3所示.

表3 计算值与试验值对比Tab.3 Comparison between calculated and experimental values

由表3可知，公式计算值与试验值之比的平均值为1，均方差为0.069，试验结果与公式吻合良好，说明公式的建立是合理的，但是由于试验的局限性，公式的准确度需要进一步验证.

5 结 论

通过对影响组合柱偏压承载力的因素进行分析，采用偏心距、混凝土强度等级以及纤维缠绕角度等因素对GFRP组合构件在偏心荷载下的承载力进行分析后发现，承载力随着配骨指标、套箍系数、混凝土强度等级的增加呈线性增加，随纤维缠绕角度的增加而增长，而长细比、偏心距的增加导致承载力下降.

本文考虑长细比对承载力的影响，对已有承载力公式进行修正，并通过与试验结果的对比验证了公式计算结果的准确性.