基于改进EWT的模拟电路故障诊断研究

王 宁，李志华，窦修超

(河海大学 能源与电气学院，江苏 南京 211100)

0 引 言

随着大规模集成电路的广泛应用，模拟电路的发展趋向于更加复杂化。其具体表现为电路元件的容差性、非线性和故障的多样性等特点，而模拟电路故障诊断的重点是在有限的输出节点提取有效的故障特征，这大大增加了故障诊断的难度。20世纪90年代，基于规则的人工智能技术得到了不断发展并成为故障诊断的主要方向，目前主要基于信号分析的故障特征提取方法为傅里叶变换[1-2]和小波变换等[3-5]。

文献[6]采用傅里叶变换来提取构成样本空间的电路输出电压特征，根据决策树定位故障。该方法的缺点是精度不理想，没有研究软故障类型，而且傅里叶变换的条件苛刻，不适用于非平稳信号。文献[7]结合小波理论和神经网络的特点对非线性电路进行诊断，但小波变换的方法易受到选取的小波函数的影响，选取不同的小波基对计算的结果影响很大，目前还缺少准确地选取小波基的系统方法。文献[8]将改进的希尔伯特黄变换应用到非线性电路中，并针对EMD的缺点进行改进，虽然诊断正确率有提升，但是EMD算法仍存在理论支撑不足的情况。

经验小波变换(EWT)是一种新型的自适应信号处理方法[9]，以小波变换为基础，是一种建立自适应小波提取信号的幅频分量的信号分析方法[10-13]。EWT通过对信号频谱进行自适应划分，构造正交小波滤波器组，将待处理的信号在频域上进行经验小波变换得到若干具有紧支撑Fourier频谱信息的模态分量，从而实现信号的特征提取。针对EWT实现需要设定分割模态个数的问题，提出自适应无参EWT的改进方法，实现了信号的自适应分解，分解后的数据用改进后的EWT进行处理，计算分解模态的能量以及边际谱总能量，构成特征向量。

1 EWT方法

基于传统的EMD方法由于采用三次样条插值、终止条件不合理、欠包络问题造成模态混叠、虚假分量、数学理论支撑不足的现象，其改进方法EEMD在一定程度上解决了频率混叠的问题，但是出现了新的计算量增大、模型复杂性增高的弊端。为解决此问题，Gilles结合小波分析以及EMD的自适应性提出了经验小波分解方法。将原始信号f(t)分解为N个模态分量fi(t)之和，即为：

(1)

其中，fi(t)为调幅调频信号(AM-FM)。

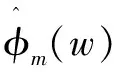
(2)

(3)

(4)

(5)

单模态个数N估算—APEWT：

经验小波变换中首先要预先估算模态的个数N，如果N过大，分解得到的模态能量过小，特征频率不明显，如果N过小，则信号分解不彻底，单分量模态复杂，不利于分析。因此，选取合适的模态个数N对后续的分析影响重大。EWT未能解决此问题，只能通过试凑的方法。结合低通滤波器电路的输出信号特点，提出了估算模态分量个数N的方法，实现了数据的自适应性驱动，即自适应无参经验小波变换(APEWT)解决模态分离个数的问题。

APEWT包括两部分，分别是Fourier谱的自适应分割以及建立基于滤波器组的小波变换，其核心是自适应地分割Fourier谱。首先计算函数的尺度空间表达形式的Fourier谱，然后分离尺度空间直方图即找到尺度空间直方图的模态分量。寻找需要的模态分量即为一个二类聚类问题，常见的方法有概率论方法和K-means方法。其次，类似于小波变换，构造动态滤波组，并用于给定信号的自适应分解。因此，通过应用APEWT方法，一个复合信号可以分解为若干个本征模态函数，相应地可以用Hilbert变换计算信号的时频信息。

文献[15]将函数的Fourier谱转换成尺度空间表示，将Fourier谱的自适应划分转化成在尺度空间上找到“有意义”的模态，文中方法的详细步骤如下：

如果直方图的模态边界关于t，局部极小值产生长尺度空间曲线为一致极小值，其才有意义。相应地，寻找有意义的直方图的模态等价于寻找一个阈值T，使得那些尺度空间曲线的长度大于T的相应曲线对应一致极小值。因此，原始问题转换为在集合{Li}i=[1,N0]的二类聚类问题。

电路不同故障元件产生的输出信号不同，其特点是具有紧致支撑的傅里叶频谱。分离出不同的故障类型就等同于分割信号傅里叶谱并将其在对应检测到的支撑频谱进行滤波。基于此，文中将这种新的特征提取方法应用于模拟电路软故障诊断中。

2 EWT故障诊断策略与步骤

假设电路的唯一可测节点为输出节点，基于APEWT的模拟电路故障诊断步骤如下：

Step1:利用PSpice对电路施加激励信号并进行蒙特卡洛分析，并将数据导入到MATLAB中。

Step2:计算各故障信号的EWT分量，根据式6计算各阶EWF与原始信号的相关系数为rj(j=1,2,…,N)[18]。

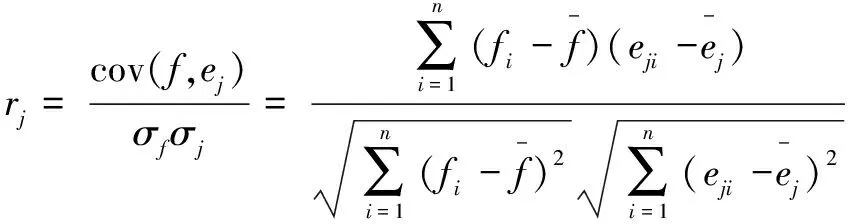
(6)

由于信号分解得到的EWF含有部分微弱信息的分量，其对分类结果产生的影响不大，选择将其删去，以减少计算的量，文中取出满足rj≥0.3的EWF分量[19]。

Step3:计算EWF分量的能量，第j个EWF的能量计算如下：

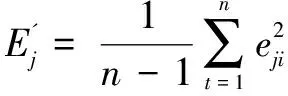
(7)

Step4:用各阶EWF与总能量的比值作为归一化能量的计算，第j个EWF的归一化能量为：

(8)

(9)

(10)

将信号幅度表示为时间和频率的函数Hilbert幅值谱，即:

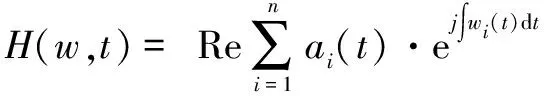
(11)

Hilbert边际谱表示不同频率幅度或能量的贡献程度，适合对原信号特征解释和提取，Hilbert边界谱能量计算如下：

(12)

将EWF的归一化能量与Hilbert边际谱总能量Ebjp，构成联合特征T=[E1E2…EpEbjp]，其中p为满足rj≥0.3的EWF分量的个数。

3 EWT模拟电路故障诊断实例

文中选取覆盖较多经典电路结构的Leapfrog benchmark电路作为诊断样本电路，其具有代表性和普遍性。实际上，Leapfrog benchmark电路是一个低通滤波器，如图1所示。

设定输入信号为调幅调频信号，幅值解调和频率解调方法能够避免传统Fourier频谱中的复杂边带分析，有效识别故障特征频率。因此选取仿真信号x(t)作为输入信号，其中x(t)由2种信号组成，分别为调频信号x11(t)和调幅信号x12(t)，如下式所示。

(13)

电阻和电容的值如图1所示，文中将电阻和电容的正常容差范围设置在±5%，经过灵敏度分析，主要有8种故障模式，分别为R1↓,R2↑,R7↓,C1↓,C2↑,C5↓,R1↓R4↑,R3↑C4↑,分别用F1～F8表示，F0为正常状态。其中，↑和↓分别表示元件大于或小于正常容差范围，若元件的标称值为X，则其软故障范围的表达为[0.5X,0.95X]∪[1.05X,1.5X]。

图1 Leapfrog benchmark电路

利用PSpice软件对电路进行100次蒙特卡洛分析，采样时间为0～0.08 s，将数据导入到MATLAB。Fourier谱分割采取尺度空间方法，解决二类聚类采用Otsu方法，经过自适应无参经验小波变换。图2为R1↓状态下输出信号频谱及每个滤波器所支撑的被检测到的边界，观察得到自适应无参经验小波变换可以分离不同的模态。

图2 仿真信号部分频谱及支撑边界

将信号分解为n个EWFs，分别计算其能量Ej(j=1,2,…,n)和其Hilbert边界谱总能量Ebjp，将Ej和Ebjp组合成特征向量。限于篇幅，表1为部分故障下的特征向量。由此看出，不同故障下的信号分解得到的EWF的能量及边际谱能量具有不同特征。模态能量主要集中在前两个EWF中，且不同的故障状态其模态分量的能量有差别，如故障F1，F5和F7。而正常状态与故障F1的模态能量基本相同，但其边际谱能量区别较大。因此提取EWF的能量特征可以较好地区分不同状态的电路状况。

表1 部分故障下EWF能量和边界谱能量

得到组合特征向量后，进行归一化处理，并将其中60次作为训练样本，其余40次作为测试样本。将提取到的特征输入到SVM分类器中，采取交叉验证方法寻找最优参数c和g，分类得到的结果如表2所示。对比改进的HHT[20]方法，可以看出文中方法的正确率较高，对比基于手动设定分解模态的EWT方法正确率略有提升。由于采用自适应无参的方法改进算法使得计算时间有所增加，但是文中方法实现了数据的自适应性分解。

表2 不同方案不同故障的诊断率 %

4 结束语

针对EWT对模拟电路故障信号分解的自适应性不足现象，提出了自适应无参的经验小波变换，利用自适应无参经验小波变换计算出单分量个数，相应确定信号Fourier谱的划分边界，然后构造滤波器组，对相应区间的频谱进行滤波，从而将信号分解为若干具有紧支撑频谱的EWF分量，再选取与原始信号相关系数较大的EWF，计算其能量与边际谱。该方法实现了数据的自适应性分解，并将这种新颖的方法应用到模拟电路故障诊断中。通过实验与EEMD对比，结果表明其不仅在提取电路的故障特征中具有较好的有效性和可靠性，而且不存在模态混叠现象，为人工智能技术在模拟电路故障在线诊断技术提供了理论支持。此外，该方法在多故障的诊断中也取得了不错的效果。