基于DELM的不确定数据流分类算法
2019-03-21刘俊杰韩东红
刘俊杰,张 昕,杨 乐,韩东红
(1.山西工程技术学院 信息工程与自动化系,山西 阳泉 045000;2.东北大学 计算机科学与工程学院,辽宁 沈阳 110819)
0 引 言
随着计算机及网络技术的飞速发展,实际应用中产生了大量不确定数据流,面向不确定数据流环境的分类处理具有重要的应用前景。基于此,研究并实现高效的不确定数据流的分类算法十分必要。受最小二乘回归法的启发,Bi等[1]提出了基于支持向量机的全支持向量分类算法(TSVC)。对有噪音的不确定数据分类问题,为提高分类准确率,一些学者采用集成分类器的方法。文献[2]提出一种基于SVM的集成分类器,采用OC-SVM方法处理不确定性,同时调整每个基分类器的权重以处理概念漂移。文献[3]提出的WE-DELM算法使用ELM技术训练基分类器并动态改变基分类器权重来跟踪不断演进的数据流。文献[4]提出UELM-MapReduce算法,即利用ELM算法对每个不确定数据流块并行训练基分类器,根据基分类器在最新的测数据集上的均方差值对相应的权重进行调整,同时替换准确率最低的分类器。
J Ma等[5]开发了有效的周期模式识别和特征提取技术,提出了一个新的处理框架来细化数据流,支持不确定数据流中的异常检测。Shajib B U等[6]设计了一种有效的数据结构,称为不确定流树以存储最近的元数据。Zhou等[7]对不确定数据流挖掘过程中top-k查询、ER-Topk查询、稀疏性估计、集合相似性和聚类进行了研究,提出了一种新的DSUF-mine算法来挖掘频繁的不确定性流。吕艳霞等[8]提出一种基于VFDT算法的WBVFDTu算法。Wang等[9]在MEME(multiple expectation-maximization for motif elicitation)的基础上,提出了一种多属性不确定数据流的基元发现算法。
文献[10]认为不确定数据流中产生了周期性概念往复。所谓周期性的概念往复,是指相同的概念可能会以相同时间间隔出现。刘志军等[11]提出一种基于自适应快速决策树的算法,实现对不确定数据流的有效分类。曹科研[12]提出了一种障碍空间中不确定数据聚类算法(OBS-UK-means),实验表明该算法能有效提高不确定数据流的聚类效率。张晨等[13]提出了EMicro算法,以解决不确定数据流上的聚类问题。
综上所述,面向不确定数据流的分类处理主要面临以下挑战:适应高速无限的数据流环境;检测并处理概念漂移及概念往复;处理数据的不确定性。
对此,文中提出一种将不确定数据向确定数据转换的方法,并且在极限学习机的基础上提出基于分块矩阵的并行极限学习机,以应对大规模的流数据;针对实际应用中不确定数据流蕴含的概念存在往复出现的特点,基于WE-DELM算法[14]提出基于概念缓冲的加权集成分布式极限学习机算法(CBWE-DELM),可以在新概念发生时模型并不需要每次都重新学习,更适用于有概念往复现象的不确定数据流的分类问题。
1 面向不确定数据流的基于概念缓冲的加权集成分布式极限学习机算法
1.1 相关定义
定义1(不确定数据元组和实例):给定一个不确定数据元组xi共有个m实例,设xi的j个实例为每个不确定数据实例的概率,则有:
(1)

定义3(不确定数据实例的分类):给定类别标签共L个,即可将实例进行分类,得到不确定数据实例属于某个类别Cl(1≤l≤L)。
(2)
即所有不确定实例属于类别的概率和。
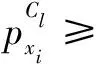
1.2 基于概念缓冲的CBWE-DELM算法思想及框架模型的实现
根据数据到达时间,将数据流分割成不相交的块,每个包含相同数量的元组;利用DELM在这n个不确定数据块上训练基分类器。为了更新集成分类模型,需要维护一个类分布表群,即所有基分类器单独保存一个类分布表,表中记录各个对应分类器的分布器概率。分类器Ej的类分布表如下:Ej,{JCl,jpcl},1≤l≤L。其中JCl为类别标签,jpcl为类别JCl出现的概率,计算方法见定义3及定义5。
在分类器更新和剪枝阶段,根据当前样本更新和缩减集合分类器,但旧的分类器被裁剪之后不会被立即删除。为了做到类似删除效果,文中设计了一个用于放置缓存的模型,用来保存旧的分类器已经出现的旧概念。然后用提出的方法来更新缓冲区管理的概念,具体方法如下:
数据块到达时,如果数据流中存在新概念,则需要更新集成分类器中的基分类器;若数据流中没出现新概念,则不需要更新。
第一步是测量缓冲区中的类分布表与新概念的类分布表之间的差异Djk,计算方式如下:
(3)
其中,jpcl为新概念的类分布表;kpcl为缓冲区中的类分布表。
CBWE-DELM算法的模型框架如图1所示,它能够实时检测随时间演化的数据漂移的同时记忆学习到的历史概念。在第Sn+1个数据块到达时,将当前数据块中所有元组单独分类,其分类结果由集成分类模型中每个基分类器投票产生。

图1 CBWE-DELM算法的模型框架

(4)
根据式5得出Ej对应的预期均方差值:
(5)
MSEr表示在数据块Sn+1上将样本xi分类为C的概率等于Ci的类分布。作随机性预测时分类器均方误差度量:
(6)
其中,P(c)(P(c)∈(0,1))表示Sn+1中每个类的占比值。
每个基分类器对第n+1个数据块Sn+1中元组xi分类完成后,首先得出Ej的预测均方差值MSEj,接着将Ej的权值设定为:WEj=MSEr-MSEj。
如果WEj≤0,建立新的基分类器E0,设其权值为WE0,用数据块Sn+1重新训练,得出E_errj和MSEj;否则认为现集成分类器对当前数据流的概念不匹配。
CBWE-DELM算法的伪代码如算法1所示。
2 实验及结果分析
2.1 实验环境
分布式环境下的实验具体设置为:Hadoop集群(版本号:0.20.2)共有8台机器,主节点设置一台,数据节点共有7台PC,所有节点均使用Linux5.6系统、Intel Quad Core 2.66GHz处理器、内存的大小设置为4 GB。
在单机环境下进行的实验中,机器使用Windows 7系统配置了Intel(R) Core(TM) i5-2450M @2.50 GHz的处理器,4 GB内存。
2.2 数据集
HyperPlane数据集常用在数据流仿真实验中,是非常好的一种模拟数据流的方法,并且可以通过改变超平面的一些特性来模拟数据流的概念漂移。
已知随机生成每个样本中服从均匀分布在区间值为0到1中的属性值xi,可以根据式7定义一个m维的超平面:
(7)
数据生成过程的第一步要随机生成xi的权重ai(1≤i≤m),其中ai∈[0,1],且a0满足如下公式:
(8)
随机样本中被标记为正样例的元素会满足式9,反之将其标记为负样例。
(9)
下面介绍如何模拟数据的概念漂移。首先定义三个变量:样本的权值、权值变化范围、权值改变方向,分别用α、β、γ表示,其中γi={-1,1}。根据α、β、γ控制概念漂移的产生过程,即据此改变固定数量的样本,每次更改都需要重新度量a0的值以创建一个新的超平面。
此外,为了验证CBWE-DELM算法对具有往复的概念漂移不确定数据流的适应性和高效性,需要使用对应数据集。周期地改变上述三个变量,形成具有概念往复的不确定数据流。对实验中的4 000 000条数据,将周期设置为500 000条,也就是说每过一次周期,改变α、β、γ的值。随机改变5次,即具有5个不同的属性权值的超平面。
设类别A、B、C、D分别对应上述周期内数据,那么实例X=(x0,x1,…,xn)根据以下情况进行类别判定:根据判定条件,可以得到10个互不相同的区间分隔500 000条实验数据。每隔500 000条记录便重复上述操作一次,确保总数据周期相同。

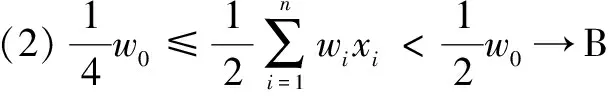
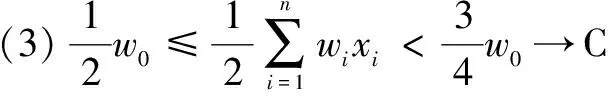

2.3 概念往复不确定数据流环境下的算法对比
实验结果如图2和图3所示。可以看出,当数据集较小时,准确率上两算法相近,没有太大差别。但是WE-DELM算法的准确率在数据集增加时显著降低,CBWE-DELM有较好的表现。从图3可以看出,在没有概念往复的小规模数据集上,由于CBWE-DELM需要建立缓冲区,所以在速度上略低于WE-DELM。然而当数据集的规模开始增大时,CBWE-DELM算法可在跟踪时间推移的数据漂移的同时记忆学习到历史概念,而WE-DELM算法不断更新的时间消耗远超过CBWE-DELM在缓冲区上消耗的时间,所以CBWE-DELM在速度上远高于WE-DELM。
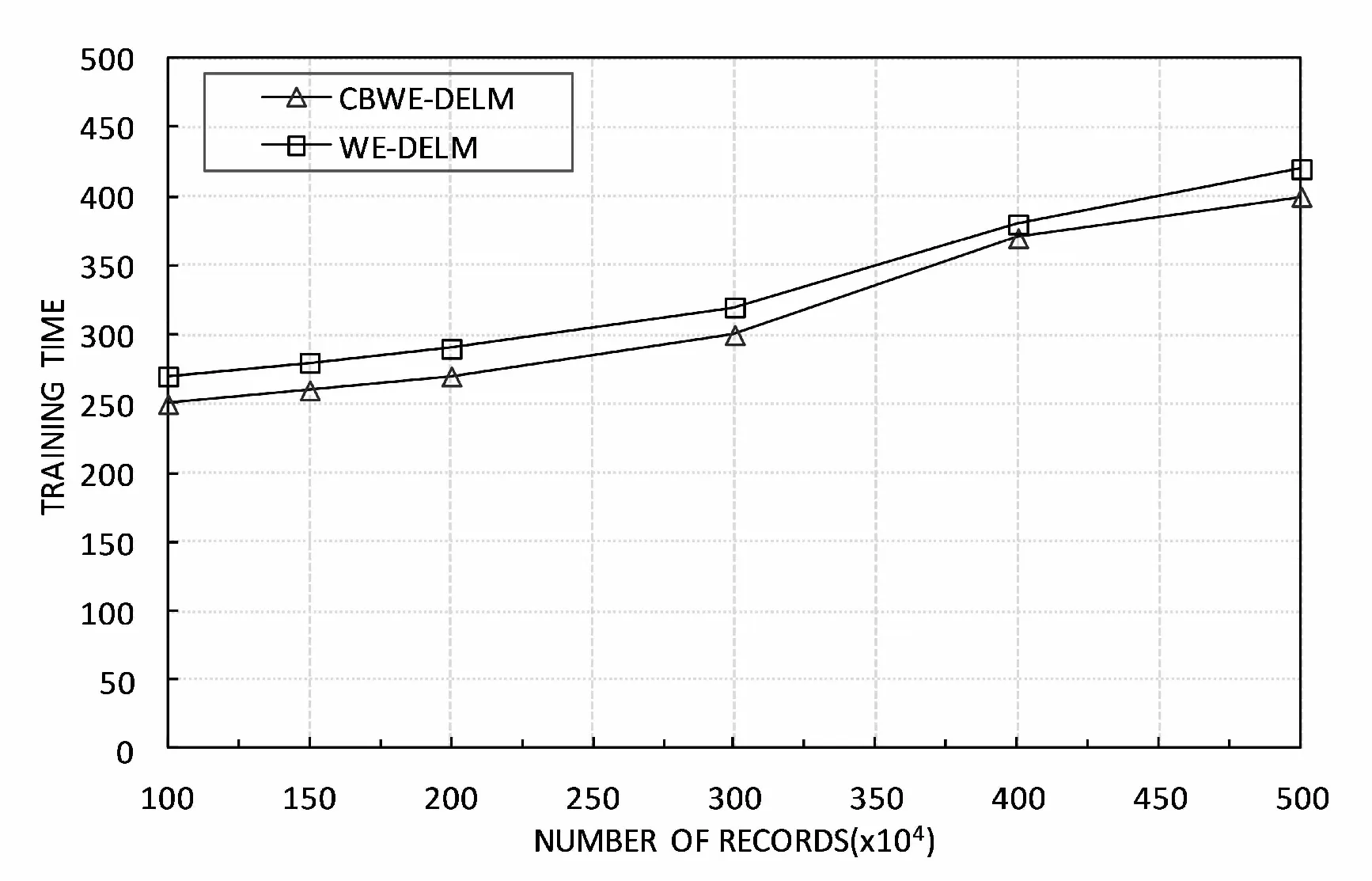
图3 训练时间曲线
3 结束语
提出的CBWE-DELM算法解决了具有概念漂移的不确定数据流的分类问题和不确定数据流的概念往复问题。在高速不确定数据流的环境下,通过在WE-DELM算法上加入可以保存历史数据的缓冲区,优化了算法性能。经实验证明,CBWE-DELM算法在性能上有着良好的提升。
