系统复杂性及度量*
2019-03-19段晓君尹伊敏顾孔静
段晓君,尹伊敏,顾孔静
(国防科技大学 文理学院, 湖南 长沙 410073)
1 复杂性语义简析
Hawking认为“21世纪是复杂性科学的世纪”[1]。复和杂两字的本意分别包含了有序和无序含义,由此显示出其复杂性[2]。对应复合度的英语Complicated意味着很难解开,复合度高的系统通常指互相牵连,难以展开成更简单的系统,即复合物、混合体;而复杂性对应的 Complexity意味着很难分析,复杂系统则是指相互依赖,每个组件的行为依赖于其他组件的行为,减少部分或者分解后不能运转的系统。从词义分析可知高复合度的系统未必有相对应的高复杂性,从而避免仅用还原论思想解释复杂性。
2 复杂性的界定
复杂性科学是关于复杂系统的微观联系及宏观功能时空演化、预测及控制规律的科学[3]。至今复杂性并没有统一的定义,因为复杂性概念是语境依赖的,因此不同语境下存在不同的复杂性语义和测度[2]。经统计,现对复杂性的定义已有45种之多;相应地,复杂系统也有十大特征[2,4]。
信息论创始人之一Wavell[5]将复杂性界定为有组织和无组织两类。Lorentz认为复杂性即对初始条件的敏感依赖性[2]。Simon给出了层级复杂性的概念,他将复杂性与系统的层次结构联系起来,认为进化着的复杂性往往表现为层级结构并且层次系统比规模相当的非层次系统进化速度快很多[6]。Prigogine等[7]的“探索复杂性”主要是指系统的自组织。美国人工生命之父Langton把复杂性理解为混沌的边缘,即复杂性最可能处在有序和无序状态之间[2]。Buck[8]认为可把复杂性理解为自组织临界性。Holland[9]认为复杂性是“隐秩序”,适应性造就复杂性。法国的Morelan认为“复杂性是辩证法的统一”,可视复杂性为有序和无序的对立统一[2]。
20世纪三四十年代,Godel、Turing等数理学家在研究数学问题的可解性时提出了计算问题,而后到60年代逐渐发展成计算复杂性理论[2];之后Kolmogorov等[10-11]提出了算法复杂性,即用描述符号序列的最短程序长度来度量该序列的复杂度,但具体应用时难以计算且具有一定的主观性。Cramer[12]将复杂性定义为系统可能状态数目的对数,此定义具有一定的主观性。他还以算法复杂性为基础定义了亚临界复杂性、临界复杂性和根本复杂性。随之又有了代数复杂性的概念[2],用求解问题所需的计算次数来度量复杂度。算法复杂性及引申都是利用随机性度量复杂性,而Gellmann利用对系统规律性的简述长度来衡量有效复杂性[2,13]。有效复杂性处在有序和无序的中间地带。文献[9]用无序函数(图1)来定义系统的复杂性,对于非平衡态,利用系统的无序函数及与平衡态的距离度量系统的复杂性;如果系统到达平衡态(即最混乱状态),或者完全有序(即距平衡态最远),则系统的复杂性消失[14]。

(a) 类别Ⅰ(a) Category Ⅰ (b) 类别Ⅱ(b) Category Ⅱ (c) 类别Ⅲ(c) Category Ⅲ图1 用无序函数刻画复杂性的三个类别[14]Fig.1 Three categories of complexity as a function of disorder[14]
构成系统不同的元素也会影响自身复杂性,Dodder和Dare将复杂性特点概括为:静态复杂性、动态复杂性、信息复杂性[15]。Manson[16]把复杂性研究分为算法复杂性、确定性复杂性和集成复杂性。Wade 和Heydari[1]从三个角度给出了复杂性的定义。①行为复杂性:将系统看成是一个黑箱,复杂性可基于系统输出的规律性和随机性来度量,用Shannon信息熵来定量描述系统的复杂性。②结构复杂性:基于系统的结构进行复杂性的测量和定义。一般而言,组成系统的单元数量越大、种类越多、构成系统的子系统结构层次越多、互相牵制,则系统结构越复杂。③建构复杂性:系统预测输出的难度决定了系统的复杂性。另外,系统设计与控制有关的复杂性,可分为结构复杂性、动力系统复杂性、构造复杂性[17]。
钱学森等[18-19]以系统再分类为基础,认为系统的复杂性包括子系统间的通信方式、子系统的定性模型、不同内容表达及获取相应知识、结构的改变等。颜泽贤等[2,20]认为复杂性是超越层级间的不能直接还原的关系。苗东升[2,21]对汉语中“复杂”一词从分形的角度进行了解读,并且探讨了十三类复杂性根源。文献[22]中提到圣菲研究所的科学家们对复杂性的理解概括为:复杂性科学是研究复杂系统在一些规则下怎样产生有组织性的行为。成思危[23]将复杂性分为物理复杂性、生物复杂性和经济社会复杂性三个方面。郝柏林[24]指出复杂性介于不确定和有序之间。吴彤[25]提出的客观复杂性包括:结构复杂性、边界复杂性和运动复杂性。杨永福[26]对复杂性概念和进化机制进行分析后,将复杂性分为结构复杂性、功能复杂性和组织复杂性三类。宋学峰[27]将复杂性科学研究按系统复杂性的客观性和相对性分为自然科学和组织行为科学两大学派,前一学派认为复杂性存在于客观系统中,而后者则认为复杂性源自于人的大脑。文献[28]梳理了钱学森形成独到的复杂性研究思路和方法论的历程,总结以钱学森的观点,复杂性实际上是开放式的复杂巨系统的动力学,是巨正则复杂系统的特征。金菊良等[29]认为,系统复杂性主要是指系统与子系统之间、子系统与子系统之间、要素与系统之间、要素与要素之间的关系呈现的各种不确定性,以及系统与外部环境之间的关系呈现出的各种不确定性。文献[30]提到不确定性是导致结构问题转化为非结构化问题或演变成复杂问题的主要因素。以复杂性命名的系统理论有复杂网络理论[31]、复杂适应系统等。
20世纪80年代中期,Larry Tesler在一段采访中对复杂性守恒定律(也称泰斯勒定律)进行了讨论:根据复杂性守恒定律,每个计算机应用程序都有其内在复杂度。这一观点主要应用在交互设计领域,复杂性在设计者和使用者两者之间进行分配,也反映出复杂度守恒定律的普适性。
3 复杂性的分类
美国匹兹堡大学Rescher[2,32]以本体论和认识论为框架,将复杂性概念分为组分复杂性(构成复杂性和分类复杂性)、结构复杂性(组织复杂性和层级复杂性)、功能复杂性(操作复杂性和通用复杂性)以及形式复杂性(描述复杂性、生成复杂性和计算复杂性),然而此分类中并没有考虑系统的规模、演化过程、行为预测、功能保持与控制等。郭雷[3]创造性地将复杂性与平衡概念关联,并从功能角度对复杂性进行分类。根据Rescher[32]的基本分类框架、郭雷[3]的从功能角度对复杂性的分类以及国内外对复杂性定义的分析,本文重新总结系统复杂性的概念分类见表1。

表1 复杂性概念的分类
第一,组分复杂性:复杂系统拥有数目繁多的组分,组分间有着多样且复杂的相互作用,要素与要素之间的关系呈现出各种不确定性。个体的适应性以及之间非线性的相互作用是决定系统复杂性的重要因素[33]。其一,构成复杂性:系统演化过程中,构成系统的不同因素会影响其自身复杂性。其二,分类复杂性:组分个体要素之间的变异以及其在空间分布上的不规则性,且由于异质导致组分的种类姿态万千而引起的系统复杂性。其三,规模复杂性:单元数量越大,单元类型越多,系统则因自身规模的增大而更复杂。
第二,结构复杂性:复杂性会随着关联结构从属性和多样性的提高以及联结数量和强度的提高而增加,整合生成结构复杂性[34]。其一,组织复杂性:组织形态复杂度的提高带来了组织结构的多样性和复杂性,开放系统在演化过程中结构状态的横向、纵向和空间分布的差异越大,系统复杂性越高。其二,层次复杂性:系统不同层级间的作用差别很大,构成系统的子系统结构层次越多,系统结构越复杂。其三,过程复杂性:在复杂系统进化和演化过程中,系统内部的组成要素间相互作用的复杂关系、系统与环境边界交互作用及系统与外部环境间的复杂作用都会产生复杂性。系统通过自组织、耗散行为和自组织临界,不断变革内部结构以及外部环境的关系,可能会出现分岔、混沌等现象,因而会在演化过程中产生复杂性[34]。系统的结构组合方式越复杂、层次越多、组分越多,系统也会越复杂。
第三,功能复杂性:针对系统中要素(属性)的平衡性与系统整体(结构)功能之间的关系来定义[3]。其一,预测复杂性:当预测系统状态演化时,复杂性可定义为系统状态或行为的不可预测性[3]。系统的预测复杂性与观测者能力、系统自身、概念、表象以及环境等因素有很大的关系。就某一个系统而言,观测者对系统关键的要素如安全性、能达性、可行性和自适应等定义的不同理解以及环境的作用等,对系统模型的建立和预测有着重要的影响。文献[35]从不确定性的角度分析了预测复杂性。其二,保持复杂性:当希望保持系统功能时,复杂性可定义为系统的功能关于系统要素平衡程度的灵敏性(脆弱性或非鲁棒性)[3]。其三,调控复杂性[3]:当改变系统功能时,复杂性可定义为如何实现系统新功能或所需功能的难度。如何根据功能对系统的要素进行合理分配,将会直接影响到系统功能的复杂性。如果从控制理论的角度看,系统的复杂性与系统的能控性、可观性或能达性均密切相关,系统设计必须平衡系统性能与复杂性之间的关系。随着系统结构、功能和规模的增加,系统中各部分之间的直接耦合与间接耦合以及系统对于自身运行结果的反馈使得系统越来越复杂,通过合理定义和量化系统复杂性,可以采取有效措施降低系统复杂性以追求更优的设计与控制效果[17]。
第四,描述复杂性:从描述系统状态的工作量、信息量及存储量角度出发定义系统的复杂性。其一,计算复杂性:解决一个问题所耗费的时间以及该过程中需要的计算机存储量带来的时间长度、操作及代价消耗等引起的复杂性。其二,算法复杂性:问题解决过程中涉及的描述、步骤、方法以及仿真程序等的无规则及随机性带来的复杂性。其三,有效复杂性:对系统规律性认识的表述长度来衡量系统的复杂性。描述复杂性是以数学的复杂性理论和信息理论为形式表现出来的,认为系统的复杂性就是描述系统特征的复杂性[20]。
在三维空间中,该分类可以看作是以基元、功能维、结构维为基准,以描述复杂性为手段体现具体表示过程来定义系统的复杂性,如图2所示。

图2 复杂性分类及哲学层面的关联图Fig.2 Category of complexity and the figure in the view of philosophy
在上述分类中,除学科角度复杂性分类[23]外,主要的复杂性定义和类型基本可以纳入到此复杂性概念分类体系之中。
4 复杂性的度量
除了系统复杂性的定义之外,更具挑战性的就是如何衡量系统的复杂性。系统复杂性的定性、定量的分析和计算方法、度量工具等方面均会面临相应的困难,以下做一简述。
第一,针对组分复杂性,主要分析系统的构成因素以及相互间作用结果的排列组合方式。Wolfram[36]以形式语言理论为基础,用元胞自动机状态的个数来度量动力系统的复杂性。广义自由度[37]是一种分形的维度,可以通过它来刻画组分复杂性。
第二,针对结构复杂性,尹建东等[38]指出拓扑熵、混沌和一些拓扑传递属性可用来刻画一个动力系统的复杂性;另外,基于动力学的非线性和物理学的非平衡态,可用不稳定性、多定态、分岔、对称破缺、长程秩序等概念描述系统的复杂性[21];文献[39]基于信息熵理论,从结构、功能分配和过程控制逻辑复杂性等方面对系统复杂性进行度量,利用正交投影方法解决了结构复杂性的多维度度量问题;而文献[27]运用五种指数方法对系统结构复杂性进行了度量,这些指数都是按照组织行为学派的观点,从心理学角度提出的,是对复杂性的一种定性刻画,定量化程度不太高;文献[17]从系统结构角度,将信息系统进行结构层次划分,然后针对层内及层间的基本单元和相互关系进行复杂性测量,主要利用Petri网、熵等方法。随着复杂网络理论的发展,复杂拓扑结构图、网络也运用于描述软件系统的复杂性。进化的复杂性往往表现为层级结构,在动态演化过程中具有近可分解性这一性质,可简化对复杂系统的描述,在寻求对复杂系统的理解时,可利用两种主要描述类型——状态描述和过程描述,二者也可互相转化[6]。
第三,针对功能复杂性,分类进行说明。就预测复杂性而言,针对获知组成要素之间的相互作用和行为的困难,可以通过约简系统状态空间、均化系统元素等来降低预测系统未来行为的困难度[1]。对于保持复杂性,信息熵是刻画系统信息量的一个度量,主要用于度量信息的不确定性,适用于分析系统在信息传输、转化过程中存在不确定性的问题。针对调控复杂性,可从功能实现和功能分配两个方面对系统功能复杂性进行度量。利用系统复杂性实现系统控制及设计主要应从系统结构的角度(系统大小、模块耦合性和划分)对系统进行研究,特别值得注意的是系统中的间接耦合、反馈循环及涌现性和突变性等[17]。
第四,针对描述复杂性,可以从信息科学和计算科学的角度给以量化[20]。关于计算复杂性、算法复杂性、有效复杂性[40-42],前文已经进行了相关描述。乔姆斯基把串行语言分成从简单到复杂的四类,就有了对形式语言的复杂性测度,基于此即有语法复杂性定义[2]。Crutchfield和Young[43-44]提出了基于统计力学的统计复杂性,在此基础上,将随机因素引入自动机,构造随机自动机ε机,以ε机的计算能力度量动力系统的复杂程度,不过构造ε机的建模过程计算量大;Shiner等[45]基于有序度与无序度,给出一种系统通用的复杂性度量方法,方法简单但偏笼统,难以反映系统的内在特征;还有比较经典的结构化程序复杂性度量方法[17]如Halstead复杂性度量;McCabe度量法等。另有基于数据复杂性的度量工具[46]。
特别值得一提的是熵,该度量工具应用较广,在以上四类复杂性中均可应用。它可以忽略层次结构直接度量系统体系结构的复杂性。系统的熵值影响因素包括系统中元素数量、类型以及元素间关系的复杂程度,所以常用信息熵来衡量系统的复杂性。就模型的复杂性而言,可以用参数个数、曲率、信息准则等来刻画参数模型的复杂性,用广义自由度、熵等刻画非参数模型的复杂性,不过广义自由度是一种经验性的研究工具。另外,通过算法信息容量[15](Algorithmic Information Content, AIC)来衡量系统的复杂性也有广泛的应用,可用最少的信息量描述算法的复杂性,最短的计算程序来表示被度量的系统。
5 数学工具及例子
系统复杂性的度量需要通过数学模型来进行定性和定量研究。在描述和解决复杂性问题过程中,将会涉及有序性和无序性、离散性和连续性、结构确定性和内在随机性、结构稳定性和机理多变性、初值敏感性和结果规律性等具有对立统一性的数学范畴。这一研究所涉及的工具至少包括代数学、数论、群论、图论、拓扑学、模糊数学、突变论、复杂网络、微分动力系统、微积分学、矩阵计算、张量、最优化理论、数值分析、博弈论、变分学、凸分析、概率论与数理统计、数据分析、科学计算、随机过程、遍历论、不确定性量化、动态规划、微分对策等数学工具,以及信息论、控制论和决策论、运筹学、最优控制理论、大系统理论等其他相关理论[3]。
在统计学中,统计模型的复杂度其实就是赋范空间的复杂度,大致可认为是与样本无关的复杂度及与样本相关的复杂度。在不考虑样本的情况下,可以通过度量熵、VC维[47]、广义链[48]和极值不等式[49]等来刻画模型的复杂性;而与样本有关的复杂度,从复杂性角度给出非参数估计的基础,即经验过程与概率集中不等式,可以通过经验过程、Radermacher过程[50]和对称不等式[49]来度量模型的复杂度,当然,在此过程中,可由与样本无关的复杂度所控制。结合有限信息系统的辨识过程,可比较辨识算法的收敛性、最优性及空间复杂性[51],可基于此进一步理解有限信息系统的复杂度。显然,在考虑统计模型的复杂度时,可从模型的分类复杂性、过程复杂性、调控复杂性、算法复杂性、计算复杂性以及有效复杂性角度出发来衡量它的复杂度。
接下来以案例形式不加证明地给出一个函数熵的上界,由此来度量系统模型的复杂性。
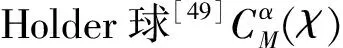
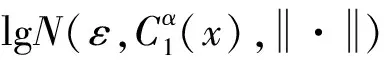
以下从概率分布的角度来分析从简单到复杂的涌现性。
例2(简单到复杂的涌现性——从泊松到幂律):复杂网络的研究方法一般是将复杂系统简化为节点及连接节点的边的集合[52]。网络的无标度性质通常是指度或入度服从幂律分布。 Matthew效应或偏好依附机制常被认为是无标度性质的原因。早在1965年, Price发现了引文网络中的Matthew效应(称之为累积效应),并建立了相应的数学模型,预测了引文网络入度分布尾端的幂律性质[53]。Price模型中,节点获得新引用的概率与已获得的引用加上某一常数成正比,与BA模型[54]类似。
Price模型与BA模型均为全局自组织网络,连边基于节点对网络节点度信息全面掌控, 这与大多数真实网络演化行为不符。引文与合作[55-57]等网络中的节点行为大部分是基于局部信息,这些模型生成同等节点规模网络的度分布和真实网络差距很大。如部分论文与作者引用次数等指标只有非常少的部分服从幂律, 而绝大部分服从广义泊松分布, 并且两个分布之间有一个过渡过程。何种机理能生成这个过程? 运用假设检验方法可以验证通过一系列泊松分布叠加可生成幂律分布[55-57]。这是一个从简单到复杂的涌现过程 (如图3所示)。
由上述可知,随着模型的不同(组分复杂性),系统的复杂性也会改变;由泊松分布到幂律分布(结构复杂性),这是系统从简单到复杂的涌现过程;此过程又存在着系统节点连接能力的多样性(功能复杂性)和表述的多样性(描述复杂性)。
6 结论

(a) 作者引用数分布(a) Distribution of the number of citations per author

(b) 合作者数量分布(b) Distribution of the number of coauthors per author

(c) 论文数量分布(c) Distribution of the number of papers per author图3 社会网络中局部自组织的几何图模型通过系列泊松分布叠加为幂律分布Fig.3 The geometric model of local self-organization in social network generates power-law by summing a range of Poisson distributions with various expected values
从复杂性语义出发,总结了国内外学者对复杂性的部分定义,并在前人的分类基础上,重新综合了复杂性的概念分类,且结合算例说明了复杂性的度量方式。由于复杂性是语境依赖的,系统复杂性暂无统一的定义。复杂性的描述方式和度量工具亦并不唯一。如:可以将复杂系统表述为一个包含异质节点、异质边和多层子图结构的超图,系统可看作更大系统的子图,环境可看作其补图;也可以从系统的规模、结构、非线性、开放性以及时间与控制层面上定义复杂性等;或可以借助其代理模型进行分析,比如基于仿真的方法、基于机理与应用的方法等。不同的研究目的及环境下,复杂性将会被赋予更丰富的含义。
