高超声速平板/空气舵热环境数值模拟研究
2019-03-19,,,,
, , , ,
(中国运载火箭技术研究院, 北京 100076)
0 引 言
高超声速机动飞行器以其高机动性和强突防能力将成为未来高超声速飞行器重要发展方向,传统轴对称再入机动飞行器以及新一代升力体飞行器是目前两类主要的高超声速飞行器。这两类飞行器均以空气舵作为气动控制部件,由于机动性的要求,飞行中存在大迎角、大侧滑以及大舵偏飞行工况,空气舵附近存在复杂的激波/边界层干扰、激波/激波干扰、边界层分离与再附等复杂流动现象[1-2],热环境分布规律和作用机理非常复杂,空气舵热环境预测成为飞行器热防护设计中的难点[3-4]。
近年来,国内一些单位针对空气舵热环境开展了风洞试验和数值模拟研究工作。在试验方面,栗继伟等[5]在中科院力学所JF-12激波风洞开展了大尺度平板/圆柱形直立舵干扰的气动热试验,结果表明距离舵根部0.2倍舵直径处的热流干扰因子高达19;贾文利[6]等在中科院力学所JF-8A炮风洞开展了空气舵缝隙及干扰区热环境测量,并针对试验状态开展了数值计算分析,获得了缝隙上下壁面热流随舵偏角和缝隙高度变化规律。在数值模拟方面,陈嘉阳等[7]对平板/钝舵缝隙内流场进行了计算分析,结果表明舵轴处热流在一定舵偏角范围内基本呈线性增加的趋势;司余[8]设计了模拟带全动舵机动导弹的简化几何模型,获得了简化全动舵区域的热环境分布规律;周佳[9]研究了缝隙高度对钝舵涡结构及热环境的影响规律,发现舵前缘平板干扰区热流随缝隙高度增加先增大再减小,而舵轴下游缝隙热流变化较小。从整体来看,目前的研究对象主要集中在钝舵干扰区其及缝隙流动,关于梯形全动舵热环境报道较少,而且目前舵轴、缝隙内热环境的产生机理和变化规律还缺乏足够认识,有必要进一步深入研究。
本文针对高超声速平板/梯形全动舵构型,首先开展了流场特征和热环境产生机理分析,然后重点分析了舵偏角、舵缝高度和边界层流态对空气舵舵轴及干扰区热环境的影响规律,并对计算结果进行了分析和讨论。
1 计算方法
1.1 计算模型和网格
为了对全动舵局部区域的流场特征和热环境分布进行精细模拟,借鉴空气舵局部测热试验研究思路,设计了一种简化全动舵模型,如图1所示。平板长度5 m,全动舵根弦长0.8 m,稍弦长0.2 m,展向高度0.3 m,前缘半径0.015 m,舵轴直径0.07 m。
本文计算采用结构化网格。图2给出了全动舵和舵轴附近网格示意图。为了对缝隙内流动进行精细模拟,舵缝内法向网格数量为51,舵轴周向网格数量为361,第一层网格高度为1×10-5m(保证壁面Y+<1),缝隙内网格总量约为250万,计算网格总量约1600万。

图1 高超声速平板/空气舵构型Fig.1 Hypersonic plate/rudder configuration

(a) 前缘附近 (b) 舵轴附近
图2计算网格
Fig.2Computationalgrids
1.2 计算方法
数值计算采用CFD++软件,气体模型采用完全气体假设,对流格式选用二阶精度的低耗散TVD格式,湍流计算采用k-ωSST模型。来流进口和上边界采用远场边界条件,计算域两侧和出口均采用零梯度边界条件;壁面采用无滑移等温壁边界条件,Tw=300 K。该计算方法在相关工程项目测热风洞试验中得到了验证。
根据飞行器飞行包线,本文选取的计算工况为:H=42 km,Ma=10,迎角和侧滑角均为零度;舵偏角范围为δr=0°~15°;缝隙高度h=3~10 mm。除研究边界层流态对热环境的影响外,本文数值模拟均采用层流假设。斯坦顿数计算公式为:St=qw/(ρ∞U∞Cp(Tw-Tr)),其中qw为壁面热流,Tr为壁面恢复温度。为了方便层流和湍流St对比,在计算Tr时,本文均采用层流普朗特数PrL=0.72。
2 典型流场特征和热环境机理分析
图3给出了平板/空气舵模型10°舵偏状态典型流场特征。从极限流线分布可以看出,平板上存在明显的气流分离再附现象(表面摩擦力线收拢于分离线而从再附线发散),其中再附线位于缝隙入口位置。另外,从空气舵迎风面极限流线分布可以看出,靠近舵根附近的气流存在明显的下洗运动,其原因是:空气舵偏转形成压缩激波,气流通过激波后压力明显上升,在展向压差的驱动下(两侧气流抽吸作用)诱导出下洗运动。此外,压力扰动通过边界层亚声速区域向两侧传播,形成展向分离流动。
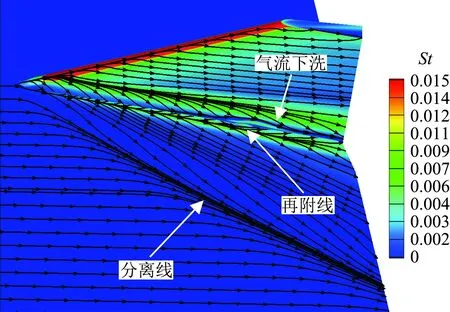
(a) 壁面极限流线分布
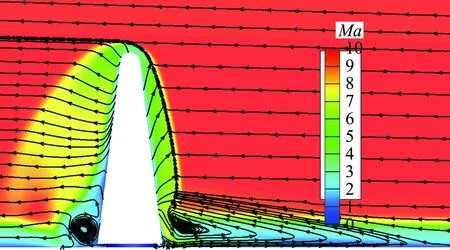
(b) 展向平面流场特征

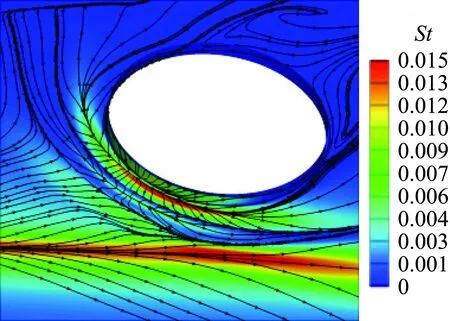
(c) 缝隙内热环境分布
图3(b)给出了位于舵轴中心位置,与空气舵纵向对称面垂直的展向平面马赫数云图分布。可以看出,在展向压力梯度作用下,靠近空气舵迎风面一侧产生了大尺度分离涡结构,这与图3(a)中的平板极限流线分布是吻合的。
图3(c)给出了缝隙内热环境分布。可以看出,在气流下洗作用下,缝隙入口边界层非常薄,从而在再附线上形成高热流条带。此外,在展向压差的驱动下,缝隙入口气流具有较高速度,缝隙内激波与边界层相互干扰,形成二次流动分离再附现象,并在一次再附线上形成高热流峰值。
3 计算结果和讨论
3.1 舵偏对热环境影响研究
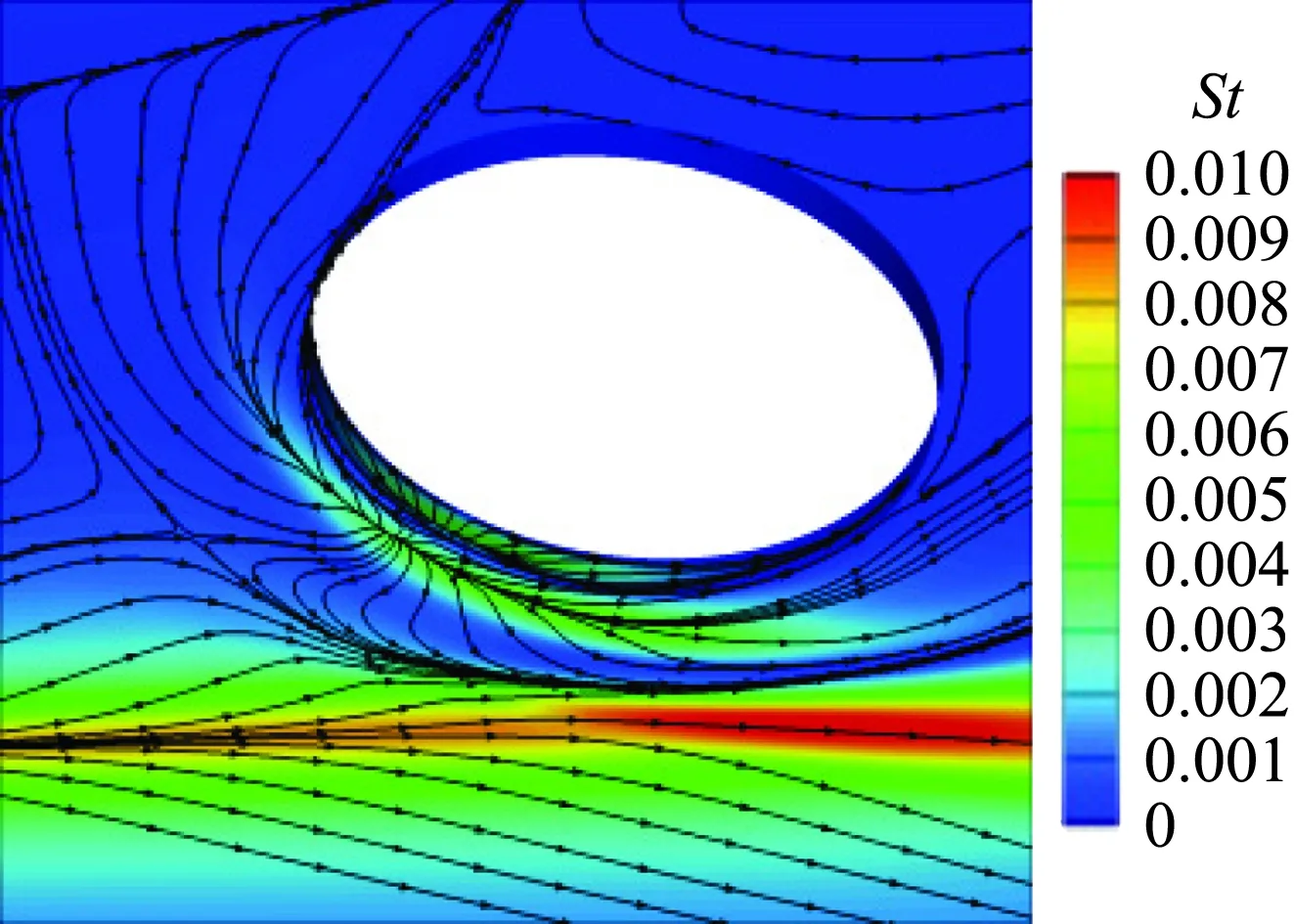
由于机动性要求,飞行器往往存在大舵偏需求,这给空气舵带来严酷的热环境。图4给出了不同舵偏条件下缝隙内热环境分布(缝隙高度5 mm)。可以看出,零舵偏状态缝隙内热环境极低,可以忽略不计;随着舵面偏转,热环境明显增加并伴随着复杂的分离流动。另外,舵偏角对分离流动结构影响很大,当舵偏大于10°时,舵轴附近流动经历了两次分离再附,其中一次再附线上热流峰值很高。
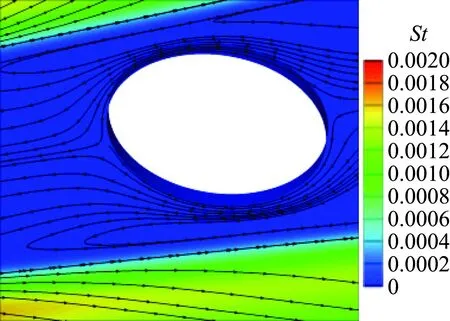
(a) δr=0°
(b) δr=5°
(c) δr=10°

(d) δr=15°
图5给出了缝隙内典型部位热环境(斯坦顿数)峰值随舵偏变化曲线。可以看出,零舵偏状态热环境很低;舵面偏转后,热环境逐渐增大,在δr=5°~15°范围内,舵轴、舵轴干扰区以及平板再附线上的热流随舵偏增加近似线性增长。另外,在较小舵偏条件下,平板再附线上的热流最高,舵轴干扰区次之,舵轴最低;当舵偏大于10°时,舵轴干扰区热流显著增大,并超过平板再附线。
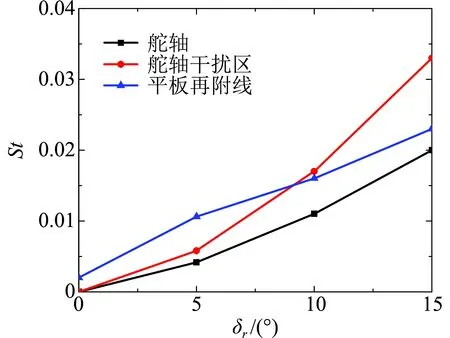
图5 缝隙内斯坦顿数峰值随舵偏变化曲线Fig.5 Variation of the peak values of Stanton number in gaps of different deflection angles
为了更好的解释舵偏对缝隙内热环境的影响规律,图6和图7分别给出了缝隙内Z=0平面马赫数和压力云图分布。在高超声速气动加热作用下,零舵偏状态缝隙入口边界层很厚,缝隙内气流速度为亚声速,热环境可以忽略。随着舵偏逐渐增大,压缩激波增强,缝隙入口压力增大,在展向压差的驱动下,缝隙入口气流速度逐渐增加。由于斯坦顿数与来流马赫数和压力正相关,所以缝隙内热环境随舵偏增大显著升高。
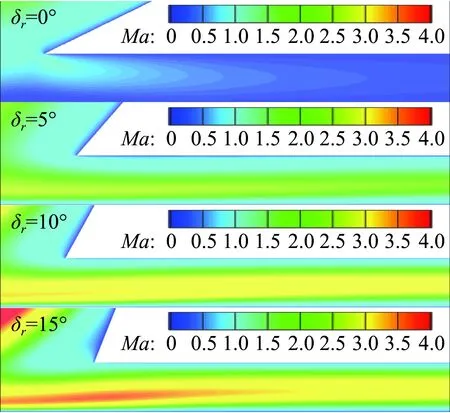
图6 不同舵偏条件下缝隙内马赫数云图分布Fig.6 Mach contours in gaps of different deflection angles
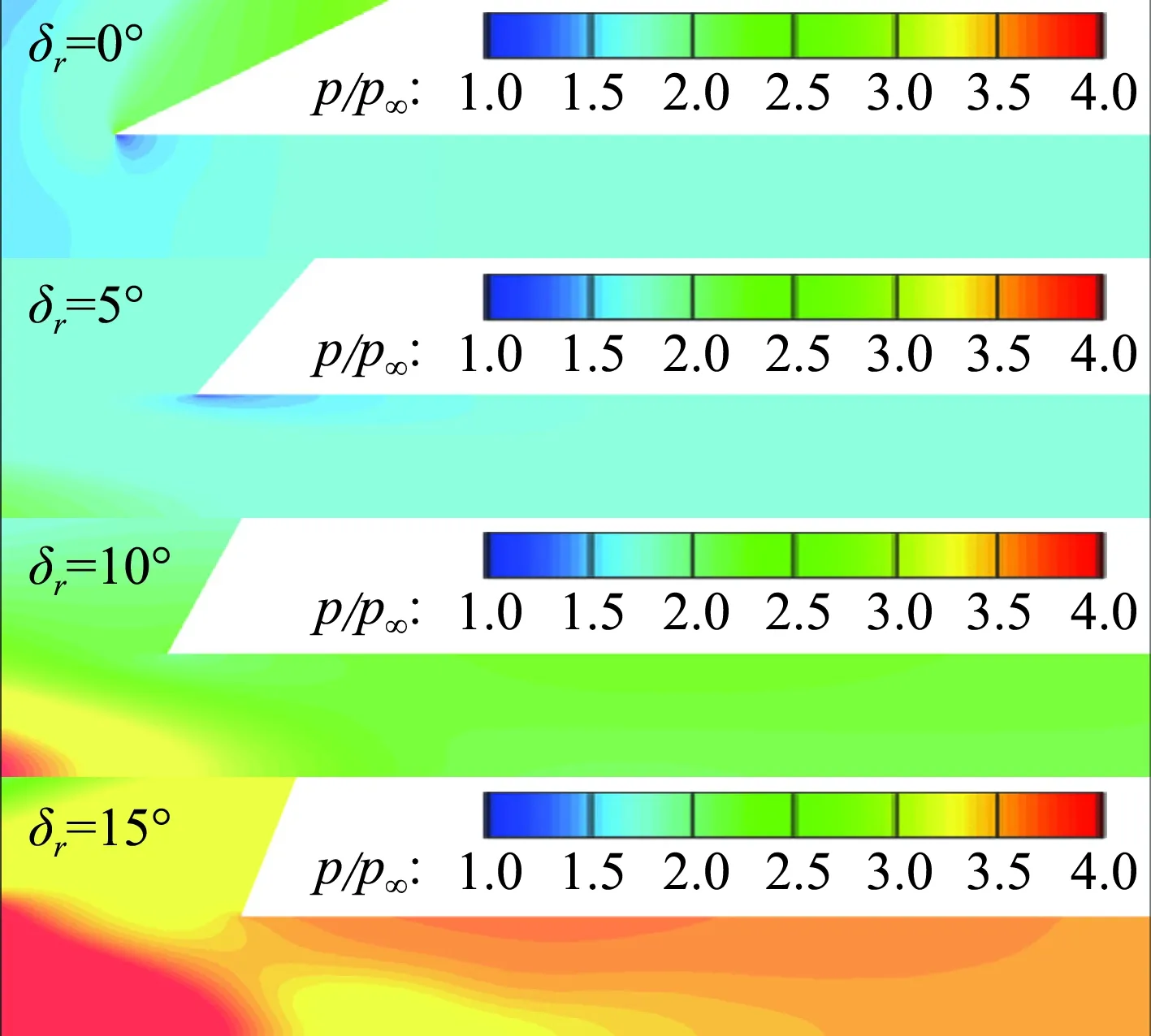
图7 不同舵偏条件下缝隙内压力云图分布Fig.7 Pressure contours in gaps of different deflection angles
3.2 缝隙高度对热环境影响研究
高超声速飞行器空气舵在生产加工和装配过程中,可能存在尺寸超差的情况;另外,飞行过程中弹体存在一定膨胀量,空气舵缝隙高度往往不是一个定值。根据工程实践经验,本文选取3 mm、5 mm、7 mm和10 mm四个典型缝隙高度开展热环境影响研究。图8给出了10°舵偏状态不同缝隙高度热环境分布,其中缝隙高度h以空气舵前未受扰动处边界层位移厚度无量纲化(δ=36 mm)。可以看出,缝隙高度对流场结构和热环境分布影响较大。当缝隙高度很小时,缝隙内热环境很低;随着缝隙高度增大,舵轴附近出现明显的分离再附流动,舵轴及干扰区热流显著增大,而且舵轴干扰区范围逐渐扩大。
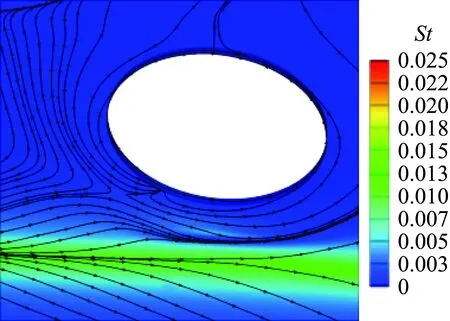
(a) h/δ=0.083
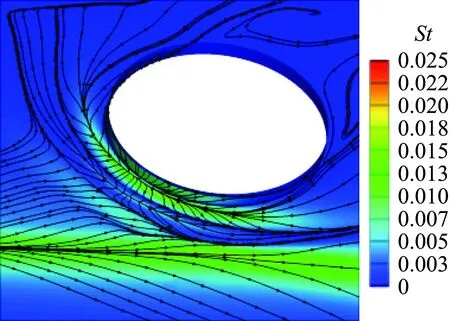
(b) h/δ=0.139
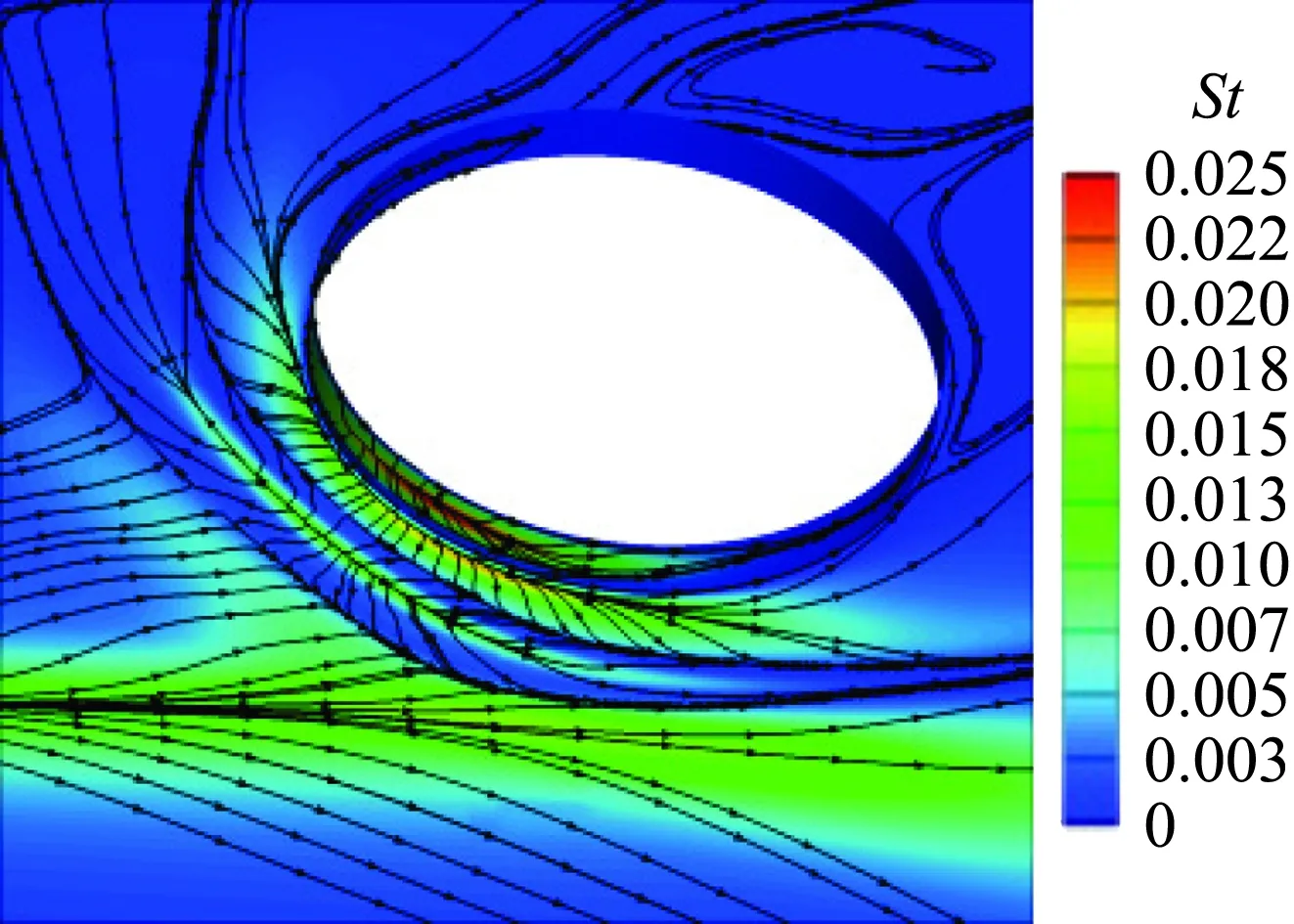
(c) h/δ=0.194
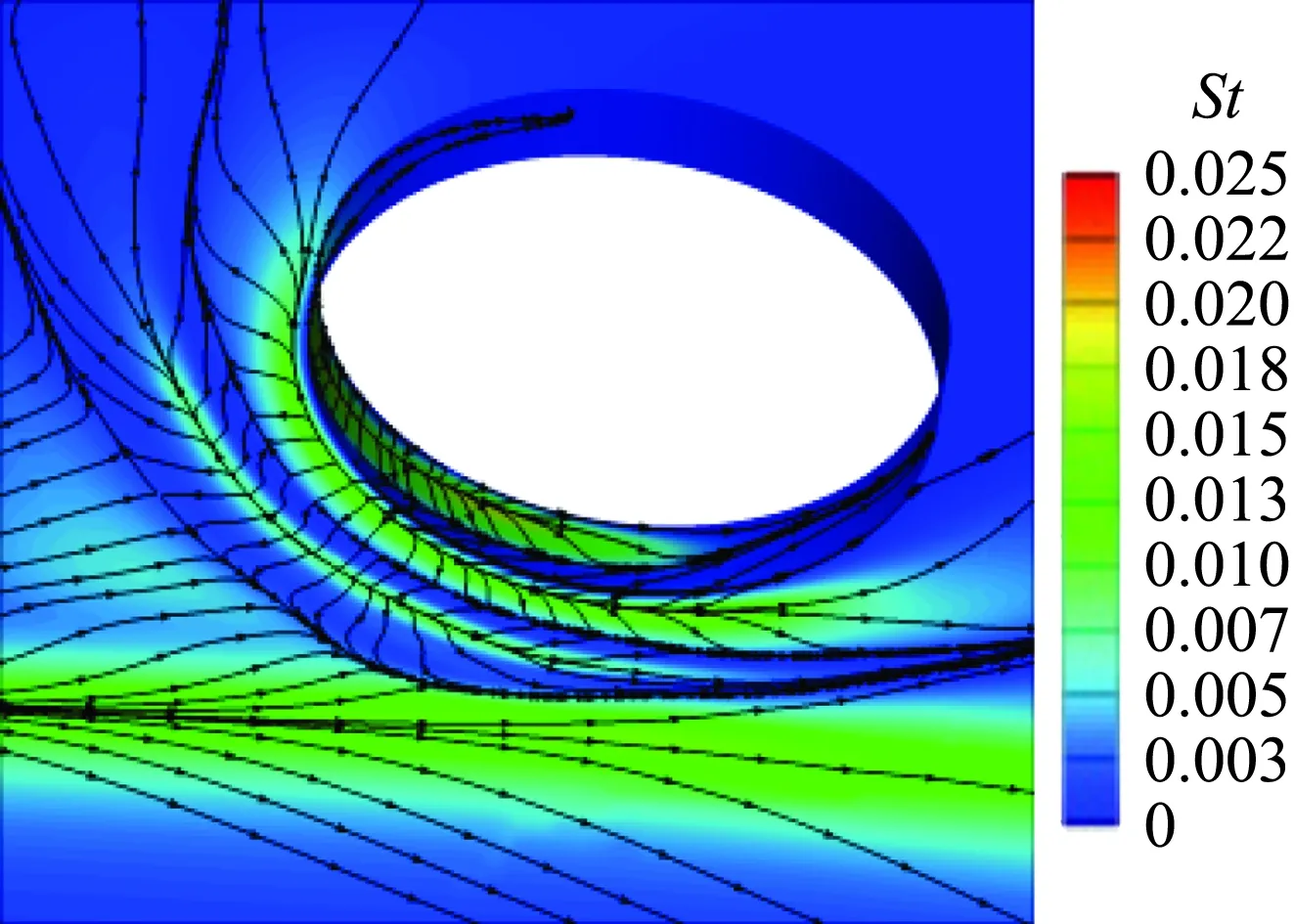
(d) h/δ=0.278
图9给出了缝隙内典型部位热环境峰值随缝隙高度变化曲线。舵轴和干扰区热流随缝隙高度增加呈现先上升后缓慢下降的趋势,但平板再附线上的热流变化不大。从图中可以看出,缝隙高度对热环境影响很大,当h/δ从0.139增大到0.194时(缝隙高度增大2 mm),舵轴热环境增加超过1倍;随着缝隙高度进一步增加,缝隙内热环境有所降低。平板再附线上的热流由气流下洗引起,与展向压力梯度(舵偏角)相关性较大,所以缝隙高度变化对其影响较小。
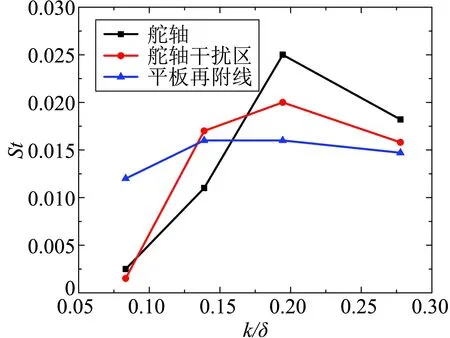
图9 缝隙内斯坦顿数峰值随缝隙高度变化曲线Fig.9 Variation of the peak values of Stanton number with gap displacement
图10和图11分别给出了缝隙内马赫数和压力云图分布。当h/δ=0.083时,壁面黏性耗散对速度损失很大,舵轴前气流速度在Ma1附近(未受扰动处),缝隙内热环境很低。随着缝隙增大,壁面黏性耗散损失减小,缝隙内流速逐渐增加。此外,由于缝隙增大使气流膨胀效应增强,缝隙入口压力逐渐降低。从压力云图可以看出,h/δ从0.083增大到0.139时,缝隙入口压力变化不大,但随着h/δ继续增加,缝隙入口压力逐渐降低。在气流速度和压力两者综合作用下,舵轴及干扰区热环境随h/δ呈现先增大而后减小的趋势。
3.3 边界层流态对热环境影响研究
对于高超声速机动飞行器,在上升段和再入飞行段都会不可避免的遇到边界层转捩问题。众所周知,对于飞行器大面积区域,边界层转捩会造成热流成倍增加,但边界层转捩对缝隙内热环境的影响报道很少。为了降低边界层转捩数值模拟的难度,本文采用全层流和全湍流进行计算分析。图12给出了15°舵偏条件下层流和湍流热环境分布对比。可以看出:(1) 层流状态热环境远高于湍流状态;(2) 缝隙内流场结构存在明显差别。层流状态舵轴附近出现了二次分离再附现象,而湍流状态只出现了一次分离,而且分离区尺寸明显大于层流状态。
图13给出了不同流态条件下热环境峰值随舵偏变化曲线。可以看出,对于舵轴、舵轴干扰区和平板再附线上的热环境,层流状态均高于湍流状态。在15°舵偏状态下,层流状态舵轴和干扰区热环境约是湍流状态的3~5倍,平板再附线上的热流也相差近1倍。在工程设计中,通常认为采用全湍流计算能够实现热环境包络设计,但最近研究结果表明,转捩边界层可能会引起更高的热流峰值[10-12]。本文计算结果也表明,对于缝隙内热环境,在边界层流态不确定的情况下,采用全湍流计算的设计方法可能会导致热环境设计条件远低于实际飞行条件,带来防热设计风险。

(a) 层流
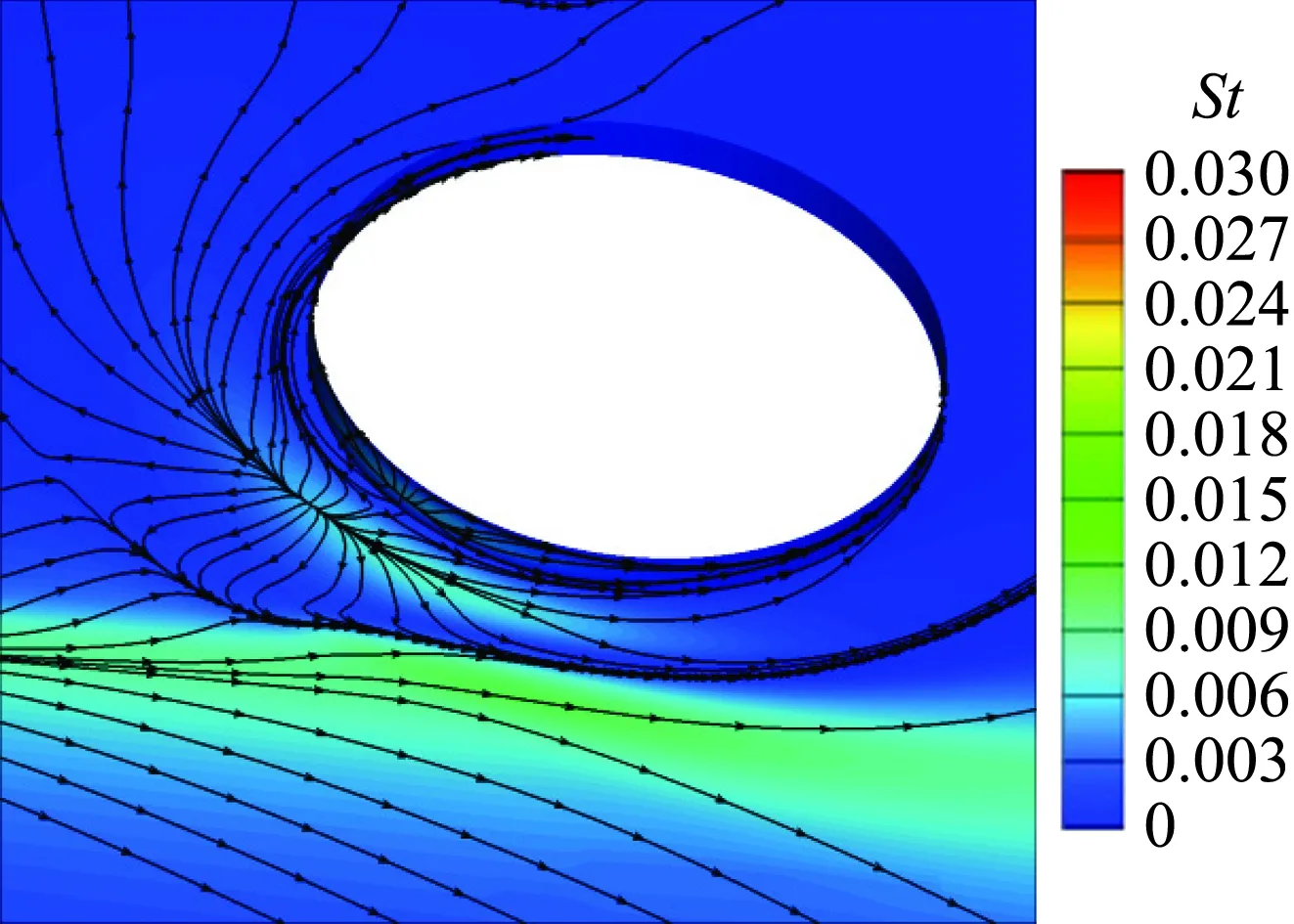
(b) 湍流
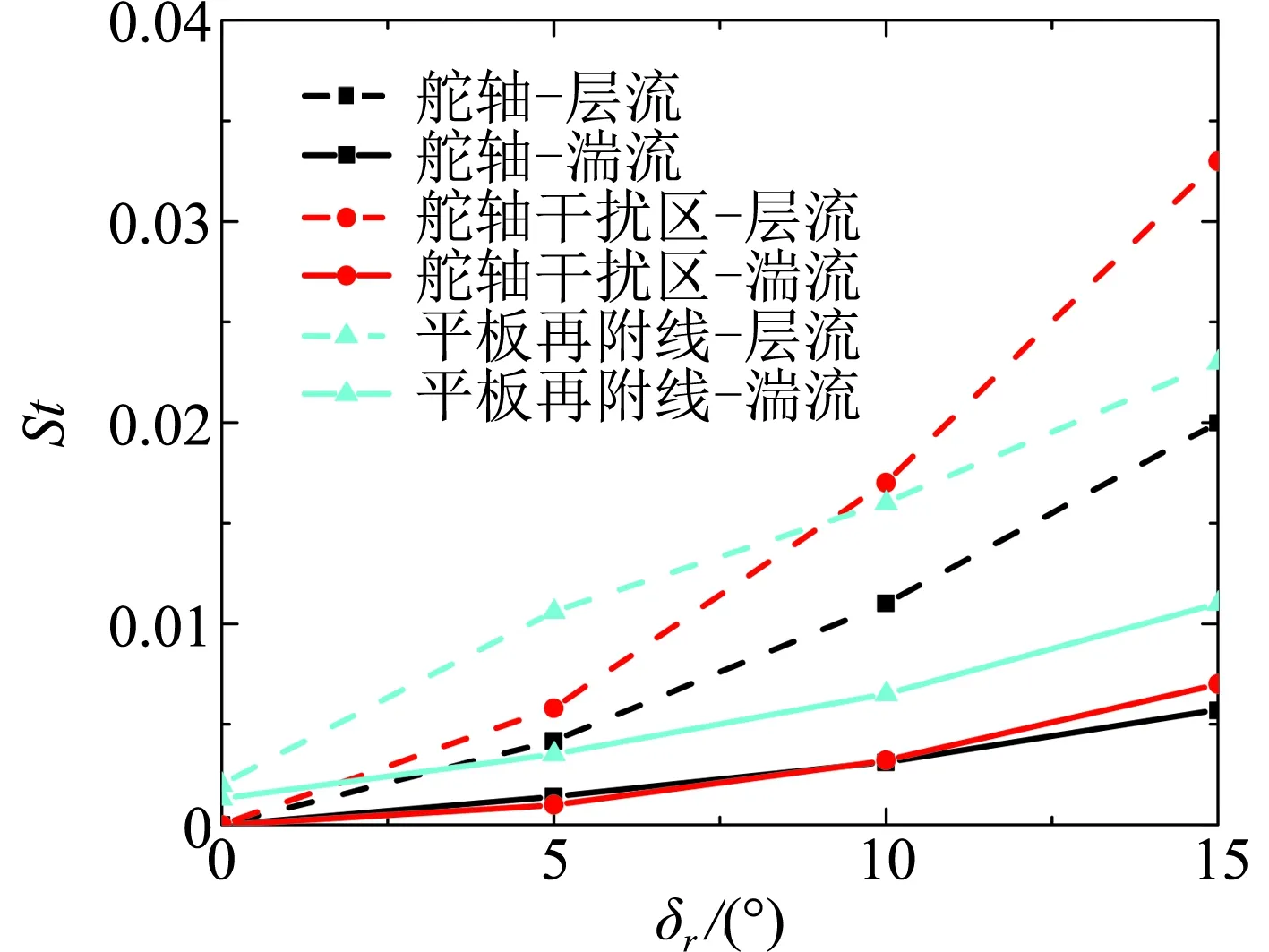
图13 不同流态条件下斯坦顿数峰值随舵偏变化曲线Fig.13 Variation of the peak value of Stanton number with deflection angles of different flow patterns
根据上述分析,我们知道影响缝隙内热环境的主要因素是缝隙入口气流速度和压力。为了更好的解释图12和图13中的物理现象。图14给出了舵缝法向高度方向对称面(y=2.5mm)以及与空气舵纵向对称面垂直的展向平面马赫数云图分布。可以看出,湍流边界层厚度约为层流状态的2~3倍,使得缝隙入口马赫数明显低于层流状态,所以其热环境较低。另外,从平板近似极限流线分布来看,由于湍流边界层速度型更加饱满,抵抗逆压梯度能力更强,所以湍流状态下分离区尺寸明显小于层流状态。
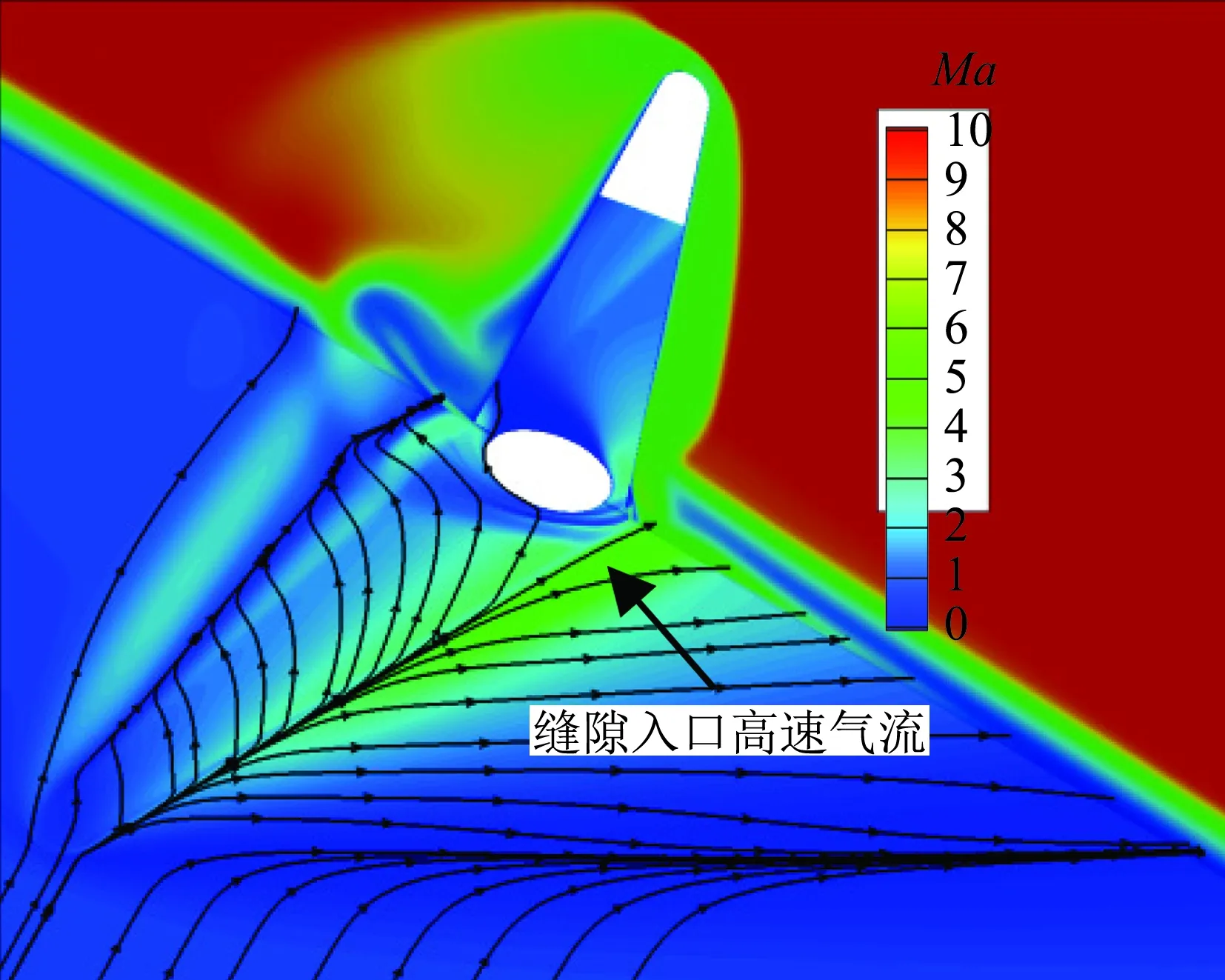
(a) 层流

(b) 湍流

图15 缝隙内马赫数云图对比Fig.15 Comparison of Mach contour distribution in gap between laminar and turbulence flow (δr=15°)
为了进一步解释层流状态热环境高于湍流的物理现象,图15给出了缝隙内马赫数云图对比。可以看出,层流状态缝隙入口气流存在明显的剪切层,速度分布不均匀;而由于湍流边界层具有较大的黏性耗散,缝隙入口气流速度比较均匀,但其平均马赫数明显低于层流状态,所以舵轴以及干扰区热环境较低。
图16给出了15°舵偏条件下层流和湍流状态舵面热环境对比。可以看出,由于展向分离涡的存在,舵面靠近根弦位置存在明显分离再附现象,对应高热流条带,由于湍流边界层更厚,所以高热流条带更加远离根弦位置。对于空气舵大面积区域,湍流热环境约为层流状态的3倍,这与传统的物理认知是一致的。
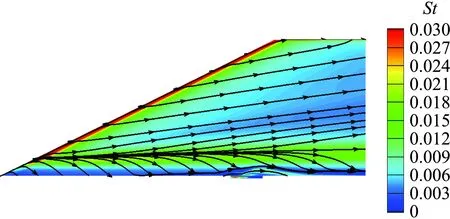
(a) 层流
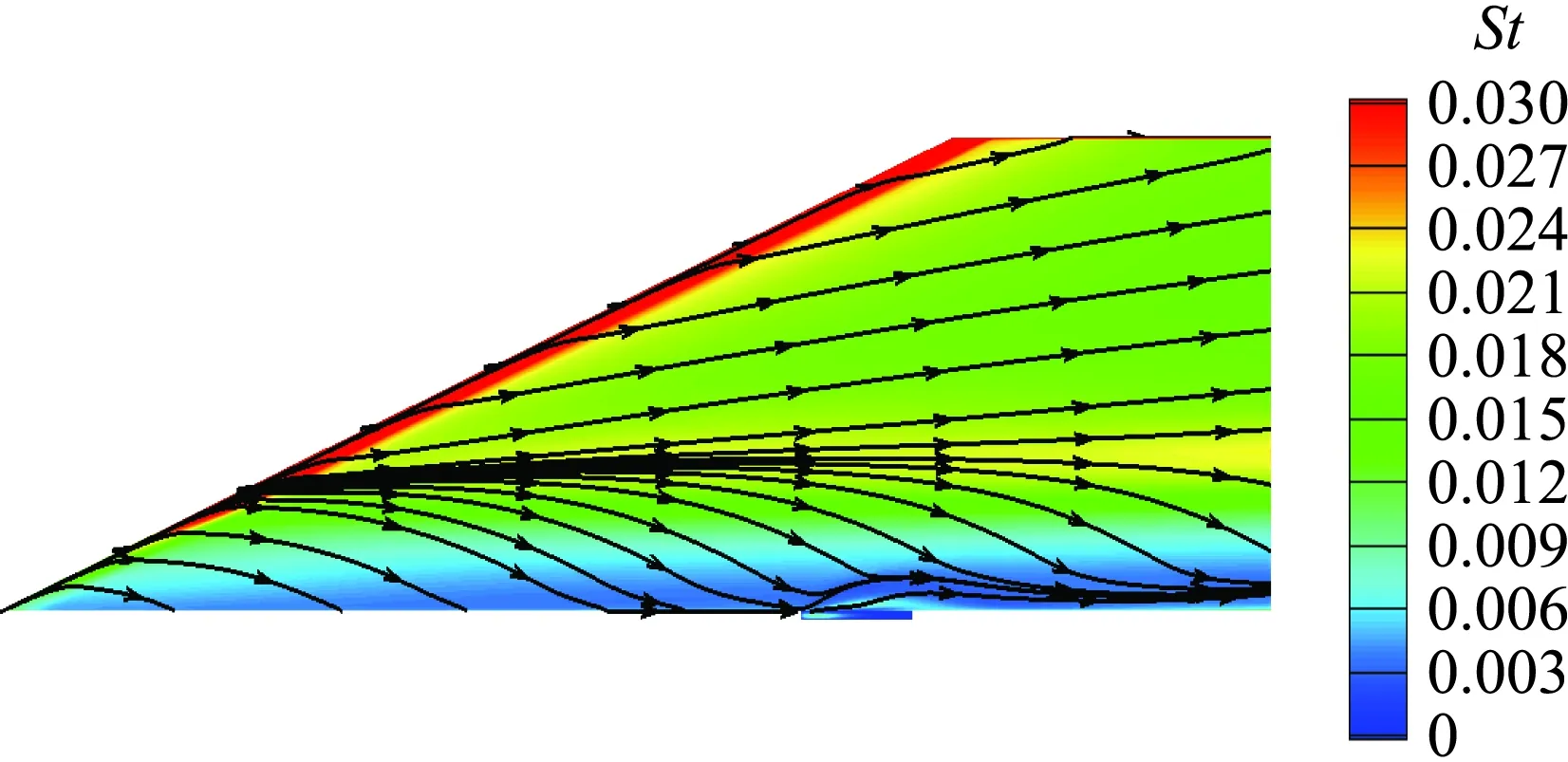
(b) 湍流
4 结 论
通过以上数值模拟计算和结果分析,可以得到以下结论:
1) 舵面偏转产生的高压气流存在明显的下洗运动,并在缝隙入口产生高热流条带;此外,在展向压差驱动下,压力扰动通过边界层亚声速区域分别向两侧传播,形成大尺度分离涡结构;
2) 零舵偏状态缝隙内流速很低,舵轴热环境可以忽略;随着舵面偏转,缝隙入口气流马赫数和压力增大,缝隙内热环境逐渐上升,在δr=5°~15°范围内,舵轴及干扰区热环境随舵偏增大近似线性增长;
3) 舵轴及干扰区热环境随缝隙高度增加呈先增加后缓慢下降的趋势,当缝隙高度由5 mm增加到7 mm时,舵轴热环境增加近1倍,但平板再附线上的热流受缝隙高度影响较小;
4) 边界层流态对缝隙内热环境影响很大,在15°舵偏状态下,层流状态热环境约是湍流状态的3~5倍,传统采用全湍流计算的设计方法可能会导致缝隙内热环境远低于实际飞行条件,带来防热设计风险。
