人工神经网络预测供热系统供水温度
2019-03-18胡江涛王新轲
胡江涛, 王新轲, 刘 罡
(1.西安交通大学人居环境与建筑工程学院,陕西西安710054; 2.成都市青羊区政府投资项目评审中心,四川成都610015)
1 概述
我国建筑供暖能耗占建筑总能耗比例逐年上升,集中供热系统的节能一直是国内外学者的研究重点。由于集中供热系统影响因素比较多,利用传统方法对供热系统供水温度的优化调节存在一定难度。
近年来,随着计算机能力的拓展,各领域应用人工神经网络(Artificial Neural Network,ANN)进行优化控制成为研究热点,暖通空调领域也不例外。Mba等人[1]用人工神经网络对高湿地区的建筑室内温度和相对湿度进行预测研究,结果证明:人工神经网络可对逐时室内温度和相对湿度进行准确预测。Neto等人[2]分别采用含有两层隐含层的人工神经网络和EnergyPlus能耗软件对巴西圣保罗大学的1幢行政办公楼的能耗进行预测,结果表明:两种方法均适用于能耗预测,人工神经网络预测结果误差更小。Jin等人[3]通过对相关系数进行计算,确定人工神经网络的输入参数,并通过计算平均偏置方差(MBE)确定了神经网络各参数的最优值,实现了对宾馆空调系统从当前室内温度变化到设定温度所需时间的精准预测。在此研究基础上,Jin等人[4]提出了新的神经网络优化方法,找到了预测供热系统从当前温度上升至室内设定温度的提前开启时间的最优人工神经网络结构,取得了精确的预测效果。冯敬芳等人[5]分别采用LM、Elman、RBF神经网络算法,对二级管网回水温度进行了预测研究,将一级管网供水温度、一级管网流量、室外温度、二级管网供水温度、二级管网流量作为神经网络的输入参数,将二级管网回水温度作为输出目标,仿真结果表明:3种神经网络均能实现二级管网回水温度的预测,RBF神经网络的收敛速度更快,预测精度更高。谢慕君等人[6]设计了一个由3层前向型神经网络与PID相结合的智能控制器,实现对二级管网回水温度的闭环控制。仿真结果表明:与常规PID控制相比,智能控制器具有调节时间短、超调量小的优点。刘庆堂等人[7]运用BP神经网络和回归预测两种方法,对供热系统供水温度和供水流量进行预测研究,分别计算两种方法的预测值与实际值的相对误差。结果表明:两种方法的预测结果均可靠,BP神经网络的预测结果更好,相对误差更小。卜云婷等人[8]采用RBF神经网络预测供热系统二级管网供水温度,并引入遗传算法对传统RBF神经网络进行改进。结合算例,对传统RBF神经网络、改进型RBF神经网络的预测能力进行比较分析,改进型RBF神经网络预测模型的预测能力更优。张震等人[9]提出了用3层的小波神经网络(WNN),将室外温度、供暖设计室内温度、供暖计算室外温度和供热面积等参数作为输入参数,对供热负荷进行预测,结果表明:24 h的预测平均相对误差仅为0.009,证明了该神经网络具有较高的预测精度。
由以上分析可知,目前的研究大多集中在采用人工神经网络实现对室内温度、供热系统热负荷等的预测,但对供水温度预测的研究比较少。本文将室内温度、室外温度、太阳辐照度作为人工神经网络输入数据,建立用于预测供水温度的人工神经网络(BP神经网络模型、Elman神经网络模型),采用试验数据对人工神经网络进行优化训练、验证,结合试验数据评价人工神经网络的预测效果(以室内温度作为评价指标),比较两种人工神经网络(以下简称神经网络)的预测性能。
2 试验系统与方案
2.1 试验系统
① 试验房间
试验房间位于西安市,西安交通大学兴庆校区土木楼1楼,试验房间位于楼内中间位置,试验期间楼内没有集中供暖。房间的进深为4.5 m,宽度为3.0 m,高度为3.5 m。外窗朝向南,宽2.0 m,高1.8 m。内门宽1 m,高2.0 m。围护结构的类型、构造、面积、传热系数见表1。
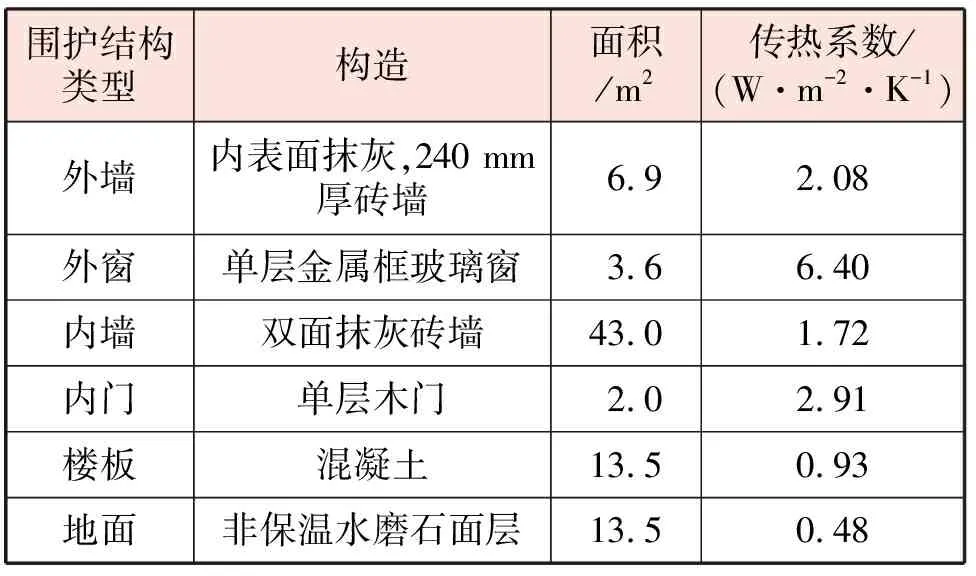
表1 围护结构的类型、构造、面积、传热系数
② 试验系统
试验数据:供水温度、室内温度、室外温度、太阳辐照度。采用PT100型热电阻采集供水温度,测量范围为-200~300 ℃,分辨率为0.1 ℃,安装在蓄热水箱出口。采用WSZY-1型温湿度自记仪测量室内外温度,测量范围为-40~100 ℃,分辨率为0.1 ℃。2个室内温度测点均选在房间的中轴线上,布置高度均为1 m,测点1距外窗1.5 m,测点2距内门1.5 m,计算室内温度时取这两个测点温度的算术平均值。室外温度测点布置在距外窗1 m的室外。太阳辐照度采用TES-1333R型太阳辐照度记录仪,最大量程为2 000 W/m2,分辨率为1 W/m2,测点布置在外窗内侧。热电阻、温湿度传感器、太阳辐照度记录仪均通过数据线连接至计算机,实现在线记录和显示等功能,数据采集时间间隔为0.5 h。
2.2 方案
笔者选取2018年1月22日11:30—2月2日22:00共550组试验数据进行神经网络的优化训练、验证,见图2。前500组作为优化训练数据,用于优化训练神经网络,确定输入层最佳输入参数组数、神经网络其他参数。后50组作为验证数据,用于验证神经网络对供水温度预测的准确性。在2018年2月4日、5日的5:30—20:30分别进行BP神经网络、Elman神经网络预测效果评价,试验系统按预测供水温度运行。在预测效果评价阶段,室内温度设定为16 ℃。
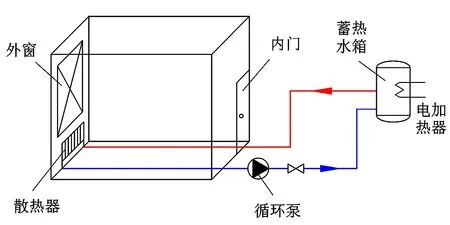
图1 试验系统的布置
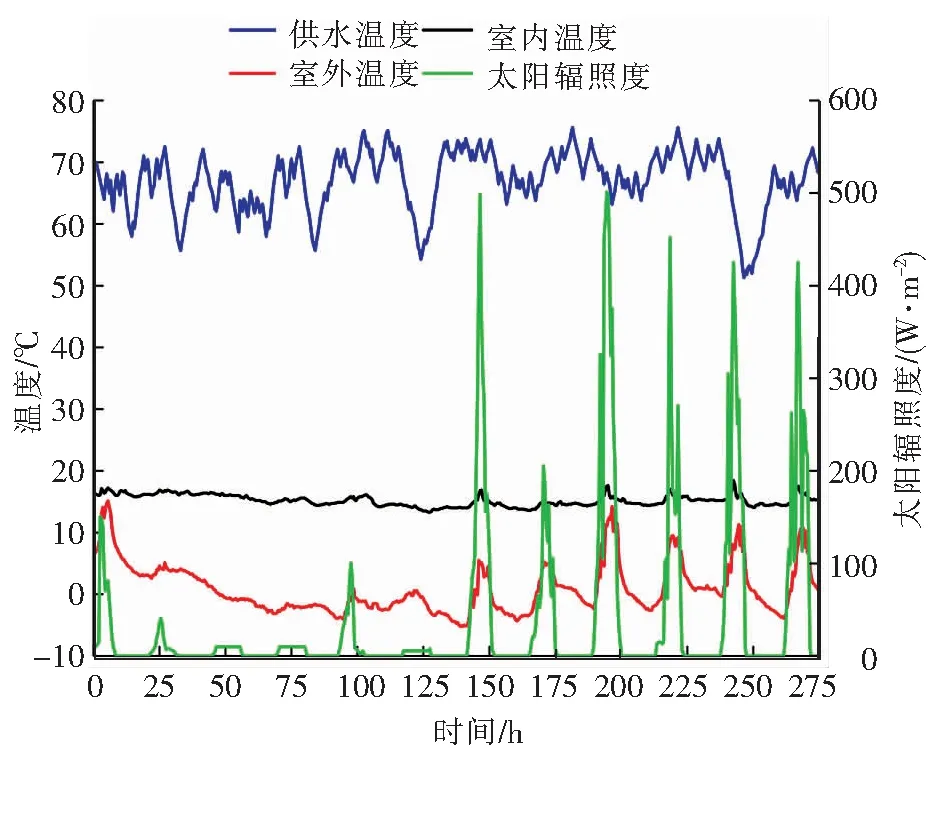
图2 用于神经网络优化训练及验证的试验数据
3 神经网络优化训练
3.1 神经网络建立
反向传播(Back Propagation,BP)学习算法简称BP算法,采用BP算法的前馈型神经网络简称BP网络。BP神经网络可以分为输入层、输出层以及隐含层,其中隐含层至少具有1层。信号由输入层节点进入神经网络,经过隐含层,并由输出层的输出节点传出。Elman是一种反馈神经网络,是在BP神经网络的隐含层中增加了1个关联层。两种神经网络的优化训练方法一致,Elman神经网络的参数可选取与经优化训练后的BP神经网络相同的参数。因此,本文仅对BP神经网络的优化训练进行分析。
BP神经网络输入层、隐含层的初始节点数量分别取3n、15,输出层节点数量为1。n的取值范围为1~10。
① 输入层节点数量为当前时刻的1组数据组(每个数据组均包括室外温度、室内温度、太阳辐照度)与前n-1时刻的数据组(每1个时刻,拥有1组数据组)。
② 输出层参数为当前时刻供水温度。
1.对代理机构的约束降低后代理机构缺乏自律。放开资格限制后,代理机构不用考虑资格的审批和升级,即使违法违规被列入不良信用记录也可以重新注册一家公司继续从业。更有甚者,有些代理公司成立的目的有可能就是代理一个较大的采购项目,项目完成后就注销,从而逃避监管。
③ 输入层到隐含层的传递函数为tangent-sigmoid,隐含层到输出层的传递函数为线性purelin函数,训练函数采用默认的LM算法进行训练,权值和阈值的学习函数采用默认的learngdm函数。最大迭代次数选取2 000,初始的学习速率、动量因子分别设置为0.5、0.5。
3.2 优化训练方法
考虑到供热系统具有延时特性,要实现对当前时刻供水温度的精准预测,须考虑当前时刻前的一段时间的室外温度、室内温度和太阳辐照度的影响,因此确定输入层输入数据组数量格外重要。此外,隐含层节点数量、隐含层层数、学习速率、动量因子等相关参数对神经网络的预测精确性有极大影响。因此,神经网络的优化训练涵盖上述所有参数。
① 输入数据组数量
在优化训练输入数据组数量时,输入数据组数量的变化范围为1~10组,变化步长为1组。此时,隐含层节点数量、隐含层层数、学习速率、动量因子均设置为初始的15个、1层、0.5、0.5。优化目标为预测当前时刻供水温度与当前时刻实测供水温度之间的均方根误差(以下简称均方根误差)达到最小。
a.当输入数据组数量为1组时:每次输入数据组为1组,将500组优化训练数据单次输入,每次输入的数据组中的供水温度即实测供水温度。
b.当输入数据组数量为2组时:输入的数据组为当前时刻的数据组与前一时刻的数据组。最先以第500组数据作为当前时刻数据组,输入的数据组为第500组、第499组,当前时刻的实测供水温度为第500组数据组中的供水温度。然后以第499组数据作为当前时刻数据组,输入的数据组为第499组、第498组,当前时刻的实测供水温度为第499组数据组中的供水温度。以此类推。
② 其他参数
在确定输入数据组数量的基础上,对神经网络其他参数进行优化训练。考虑到隐含层节点数量与隐含层层数之间、学习速率与动量因子之间存在某种耦合关系,因此采用组合寻优的方法。
第1步,隐含层节点数量与隐含层层数进行组合优化,隐含层节点数量变化范围为1~20个,变化步长为1个。隐含层层数变化范围为1~10层,变化步长为1层。学习速率、动量因子取0.5、0.5。当隐含层节点数量取1个时,隐含层层数分别取1~10层。当隐含层节点数量取2个时,隐含层层数分别取1~10层,以此类推。优化目标为均方根误差最小。
第2步,在确定隐含层节点数量、隐含层层数的基础上,对学习速率、动量因子进行优化训练,学习速率、动量因子的变化范围均为0.1~1.0,变化步长均为0.1。优化的目标仍为均方根误差最小。
3.3 优化训练结果
① 输入数据组数量
均方根误差随输入数据组数量的变化见图3。由图3可知,当输入数据组数量为7组时,均方根误差达到最小。因此,输入数据组数量取7组。
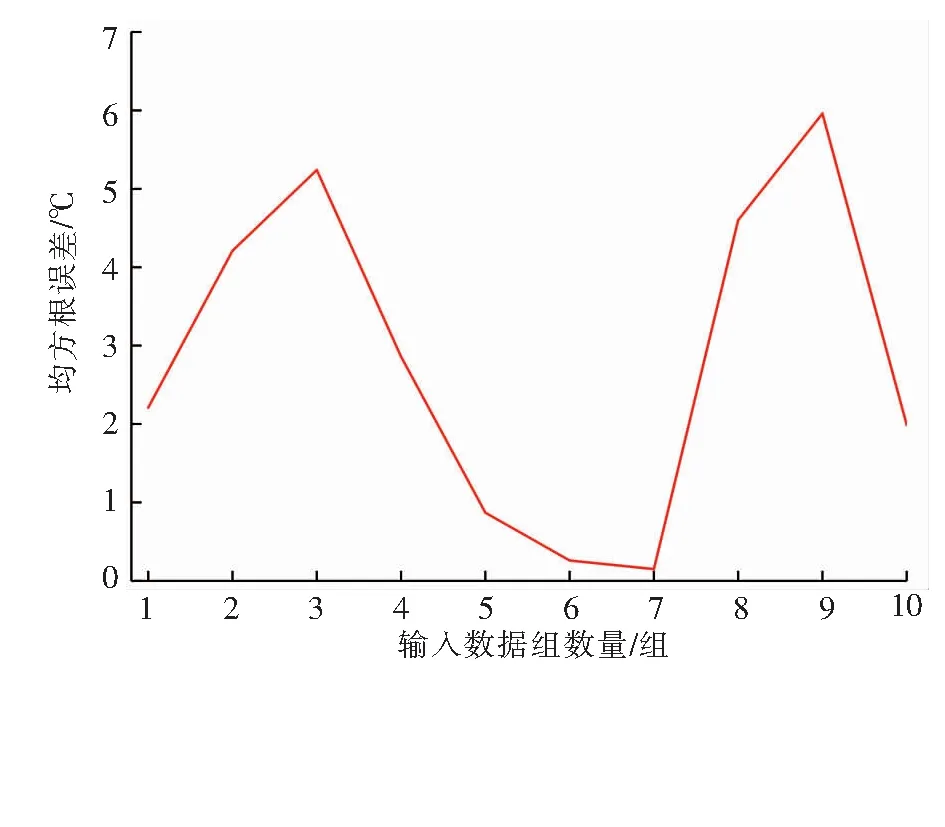
图3 均方根误差随输入数据组数量的变化
② 其他参数
输入数据组数量取7组,学习速率、动量因子分别为初始值0.5、0.5时,均方根误差随隐含层节点数量、隐含层层数的变化见图4。由图4可知,当隐含层节点数量、隐含层层数分别为18个、1层时,均方根误差达到最小。因此,隐含层节点数量、隐含层层数分别取18个、1层。
输入数据组数量取7组,隐含层节点数量、隐含层层数分别取18个、1层时,均方根误差随学习速率、动量因子的变化见图5。由图5可知,当学习速率、动量因子分别为0.3、0.6时,均方根误差达到最小。因此,学习速率、动量因子分别取0.3、0.6。
③ 优化训练结果
BP神经网络的输入数据组数量取7组,隐含层节点数量取18个,隐含层层数取1层,学习速率取0.3,动量因子取0.6。
3.4 Elman神经网络优化训练结果
Elman神经网络的参数选取与经优化训练后的BP神经网络相同的参数。
4 神经网络验证
① BP神经网络
对于BP神经网络,采用50组数据(第501~550组数据)得到的供水温度预测值与实测值随时间的变化见图6。在预测前6个时刻的供水温度时,缺少的数据组选用前500组中的数据组,在采用Elman神经网络进行预测时,也采用同样方法处理。由图6可知,由BP神经网络预测的供水温度与实际供水温度变化趋势基本一致,最大相对误差为-5.66%。
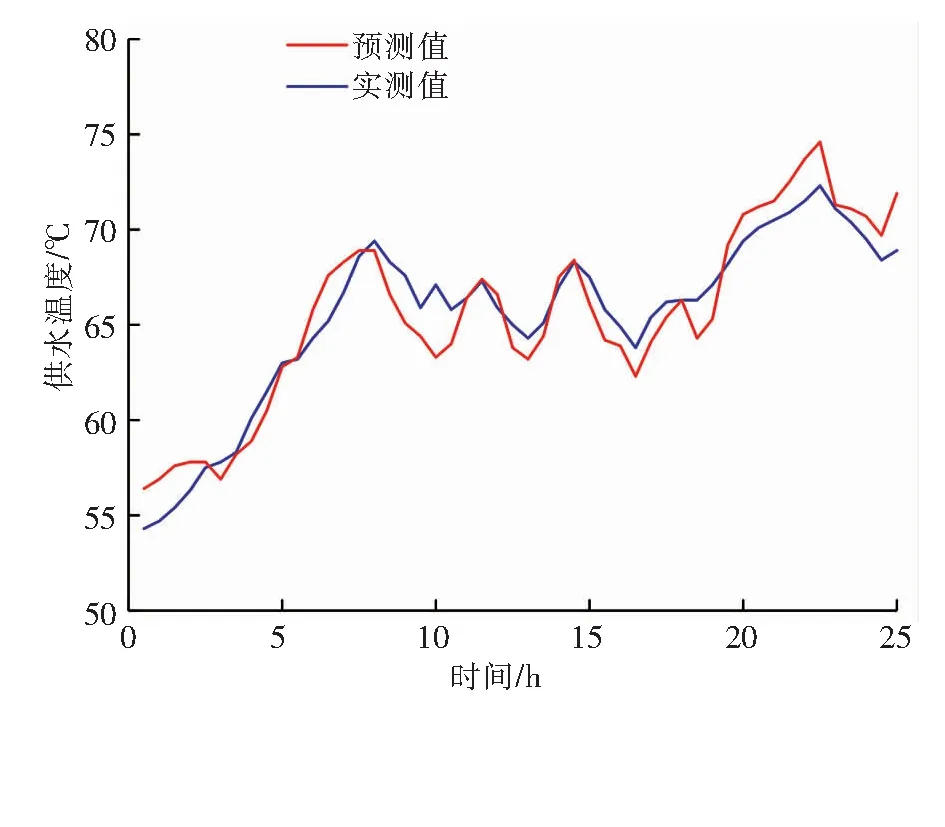
图6 由BP神经网络得到的供水温度预测值与实测值随时间的变化
② Elman神经网络
由Elman神经网络得到的供水温度预测值与实测值随时间的变化见图7。由图7可知,由Elman神经网络预测的供水温度与实际供水温度变化趋势基本一致,最大相对误差为4.32%。
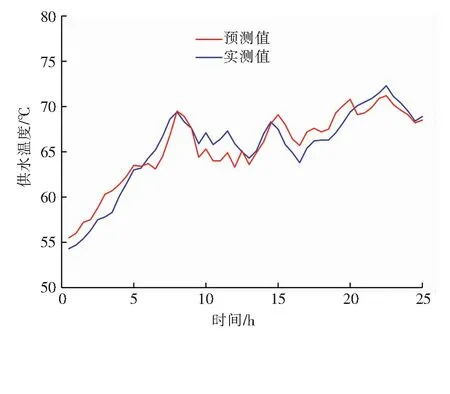
图7 由Elman神经网络得到的供水温度预测值与实测值随时间的变化
5 预测效果评价
① BP神经网络
在2018年2月4日5:30—20:30进行BP神经网络预测效果评价,数据采集时间间隔仍为0.5 h。由于BP神经网络输入的数据组数量为7组,因此实际预测时间为8:30—20:30,5:30—8:30采集的7组数据作为预测8:30供水温度的数据输入BP神经网络。Elman神经网络采用相同的处理方法。
由BP神经网络预测的供水温度、实测室内温度见图8。由图8可知,由BP神经网络预测的供水温度,可以维持室内温度,与设定室内温度(16 ℃)相比,波动范围为±1 ℃。
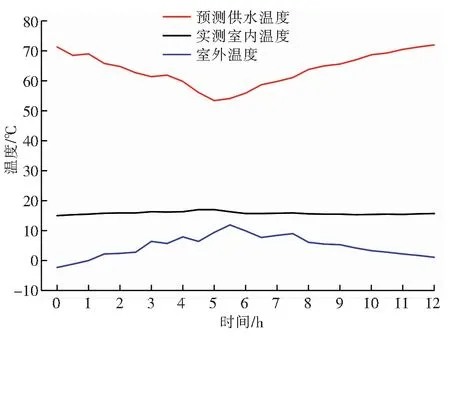
图8 由BP神经网络预测的供水温度、实测室内温度
② Elman神经网络
在2018年2月5日5:30—20:30进行Elman神经网络预测效果评价,由Elman神经网络预测的供水温度、实测室内温度见图9。由图9可知,由Elman神经网络预测的供水温度,可以维持室内温度,与设定的室内温度(16 ℃)相比,波动范围为-0.8~0.9 ℃。
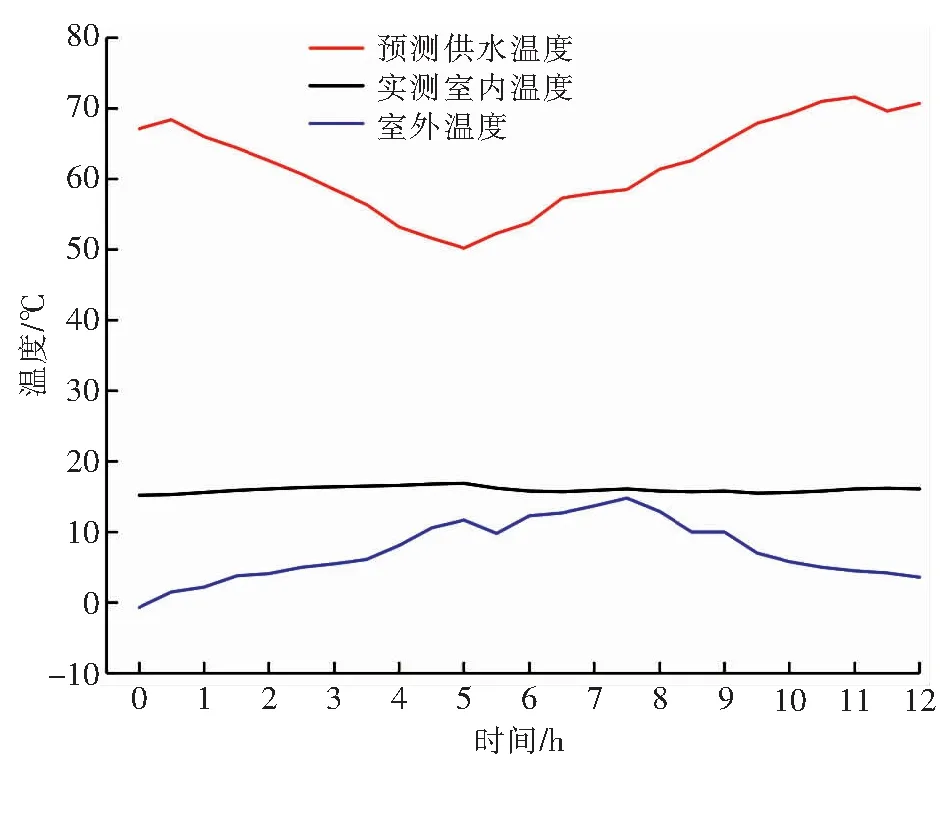
图9 由Elman神经网络预测的供水温度、实测室内温度
6 结论
① 两种神经网络的输入数据组数量均为7组(即为实现供水温度的预测,除当前时刻试验数据组外,还应输入前6个时刻的数据组)。
② 由BP神经网络、Elman神经网络预测的供水温度与实际供水温度变化趋势基本一致,最大相对误差分别为-5.66%、4.32%。
③ 由BP神经网络、Elman神经网络预测的供水温度,可以维持室内温度,与设定的室内温度相比,波动范围分别为±1 ℃、-0.8~0.9 ℃,Elman神经网络的预测能力更强。
