高速转向工况下轮毂式电动汽车电子差速控制设计
2019-03-16王东涛
王东涛
(湖南汽车工程职业学院车辆工程学院,湖南 株洲 412000)
0 引言
轮毂式电动汽车将驱动电动机分散布置到4个车轮,相对于传统的集中式驱动电动汽车而言,拥有动力传输效率高、车内空间利用率大等得天独厚的优点[1-2]。但由于轮毂式驱动电动汽车无机械式差速器,高速转向工况下不协调的车轮转矩可能会导致轮胎磨损加剧或车辆横向失稳。文献[3-4]基于阿克曼转向模型通过各种控制策略以控制车轮转速,从而得以实现电子差速控制。然而,基于此模型的电子差速控制策略只能在低速转向时发挥其有效性。在高速转向工况下,不仅需要协调车轮的转矩,还需要确保车辆不发生失稳。文献[5]在高速转弯工况下,基于模糊滑膜控制对轮毂式电动车实施稳定性控制,采用转矩平均分配的方法,并未考虑转向工况下车轮转矩差速分配问题。文献[6]通过垂直载荷的比例进行转矩差速分配,文献[7]提出转向与差动驱动联合控制策略,文献[8]通过车辆转向特性对车轮转矩执行规则分配。虽然这些研究都能很好地控制车辆发生失稳,同时满足车辆的差速特性,但都未涉及转矩的约束条件。针对高速转向工况,本文提出基于LQR的电子差速控制策略,并对车轮转矩实施差速分配,同时考虑车轮转矩的约束问题。当车速处于高速行驶状态时,在协调各车轮转矩的前提下实现电子差速功能。
1 车辆动力学模型建立
1.1 8自由度轮毂式电动汽车动力学模型
分别搭建包括纵向、侧向、侧倾、横摆运动,以及车轮的旋转运动的轮毂式电动汽车8自由度动力学模型(图1),运动微分方程如下[9]:

图1 8自由度轮毂式电动汽车动力学模型
1)车辆纵向运动
(1)
2)车辆侧向运动
(2)
3)车辆侧倾运动
(3)
4)车辆横摆运动
(4)
5)4个车轮的旋转运动
(5)
式中Fair和Fw分别为车辆迎风阻力和车轮滚动阻力,分别表示为:
Fair=0.5CDAρvx2,
(6)
(7)

1.2 轮胎模型
针对轮毂式电动汽车转向工况下轮胎的特性,本文考虑Dugoff非线性轮胎模型。轮胎垂直载荷计算公式可以表示为:
(8)
(9)
(10)
(11)
其中Fl=ax(mufhuf+mshs+murhur)/l。
各个车轮的轮胎侧偏角数学表达式如式(12)~(15):
(12)
(13)
(14)
(15)
式中δ为前轮转角。
车轮的滑移率表示为:
(16)
Dugoff轮胎模型根据摩擦椭圆理论,可以表示为:
(17)
式中μ为路面附着系数。
(18)
轮胎的纵向力和侧向力分别可以表示为:
(19)
(20)
式中:C1=C2=Cf,C3=C4=Cr;μ为路面附着系数;huf和hur分别为前、后簧下质量质心高度;lfs和lrs分别为质心到前后轴的距离;l为前后轴的距离;muf为前轴簧下质量;mur为后轴簧下质量;δf为前轮转角;Cx为轮胎纵向刚度;Cf为前轮纵向刚度;Cr为后轮纵向刚度;tw为轮距;εr为路面附着系数折算因子。
1.3 二自由度车辆动力学模型
此模型中的横摆运动、侧向运动微分方程分别如式(21)~(22)所示:
(21)
(22)
式中:Fyf=2Cf(δ-β-(lfγ/vx)),Fyr=2Cr(-β+(lrγ/vx)),β=vy/vx,M为直接横摆力矩。
2 电子差速控制器设计
2.1 二自由度期望模型
二自由度期望模型可以表示为:
(23)
2.2 基于LQR的横摆力矩控制器设计
2自由度车辆状态方程可以表示为:
(24)
式中:
考虑直接横摆力矩的2自由度车辆状态方程如下所示:
(25)

(26)


(27)
评价指标:
(28)
式中Q和R为权系数矩阵,最优的控制量可表示为
U*(t)=-Kx(t),
(29)
反馈系数K可以表示为
K=R-1BP,
(30)
P·A+AT·P-P·B·R-1·BT+Q=0。
(31)
令R=1,Q可以表示为
评价指标:
(32)
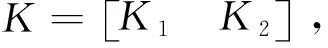
(33)
2.3 转矩分配控制策略
驱动轴的需求转矩Tm在不考虑车辆爬坡工况时,Tm计算公式如式(34):
Tm=Rw(Fair+Fw)。
(34)
考虑车轮转矩的约束条件,两侧驱动轮转矩分配如式(35)~(36)所示:
(35)
(36)
式中:Tpeak表示最大驱动转矩或制动转矩;ΔT表示车轮转矩增加量或减少量;Tb表示右侧车轮转矩;Td表示左侧车轮转矩。
3 电子差速控制性能分析
采用方向盘鱼钩输入来模拟车辆工况。车辆0~1 s时作方向盘保持不变的匀速直线行驶,路面附着系数μ=0.8,随即方向盘转角从0°阶跃为120°,如图2所示。当车速为80 km/h时,其仿真结果分别如图3~6所示。
如图3所示,4个车轮的转矩,车辆行驶到第2 s时,此刻右侧车轮转矩大于约束条件,则输出500 N·m的峰值转矩,车轮转矩满足车辆转矩约束的同时符合车辆转弯时电子差速控制的转矩分配,即外侧车轮大于内侧车轮。图4的仿真结果反应了4个车轮的滑移率变化,各个车轮的滑移率得到了良好的控制,保证了驱动轮的工作在稳定区域内。图5和图6的仿真结果可以看出,当车辆行驶到第2.5 s时,无控制的横摆角速度和质心侧偏角逐渐远离期望值,表明此时车辆已经趋于发生横向失稳状态。而采用电子差速控制的实际横摆角速度始终跟随着目标值,实际质心侧偏角与期望值的误差始终控制在较小的范围内,仿真过程中横摆角速度和质心侧偏角始终处于收敛状态。
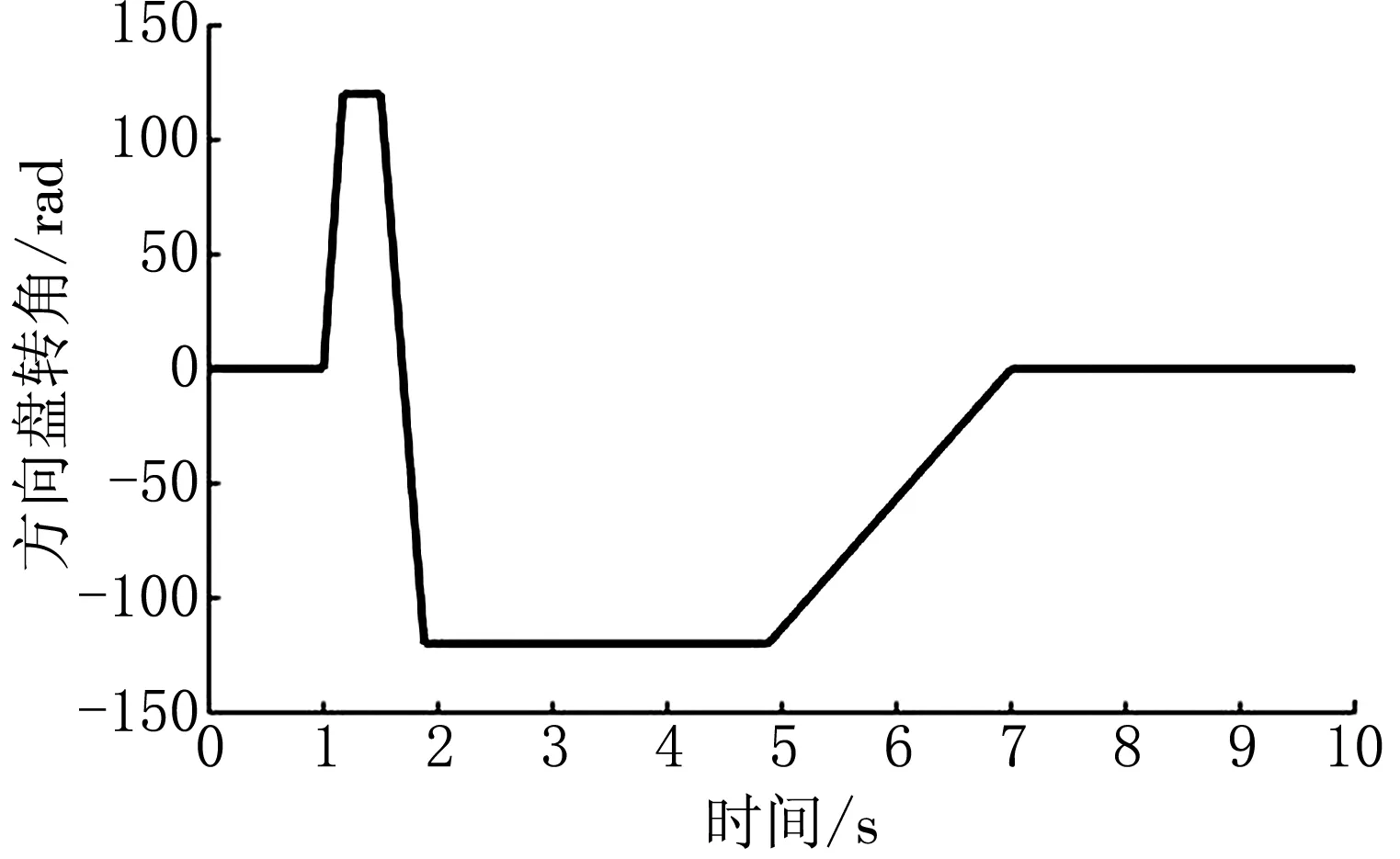
图2 方向盘转角

图3 输入转矩仿真结果

图4 滑移率仿真结果

图6 质心侧偏角
4 结语
以轮毂式电动汽车的电子差速控制为研究对象,考虑转矩的约束条件,提出了高速转向工况下的电子差速控制策略,得到如下结论:
1)制订了基于LQR的电子差速控制器,当车辆高速转向工况下时,实际横摆角速度和质心侧偏角能控制在理想范围内。
2)提出了基于高速转向工况的车轮转矩分配策略,考虑峰值转矩的约束,不仅满足车辆转弯时转矩的差值分配,同时保证了车轮滑移率控制在较小范围内。
