一种多粒度增量属性的聚类方法
2019-03-13刘杭雨
刘杭雨,于 洪
(重庆邮电大学 计算智能重庆市重点实验室,重庆 400065)
1 引 言
聚类分析是研究对象分类问题的一种统计分析方法,是数据挖掘中比较重要的概念,作为数据挖掘算法中常用的一种无监督的技术方法,已经广泛地应用在许多实际应用领域中,其优势在于不需要标记数据信息从而增加计算量[1].
现在数据的规模、种类、速度和复杂度都远远超过了人脑的认知能力,如何有效完成对大数据的认知,给传统聚类算法也带来了巨大挑战[2].目前大多数聚类方法只能处理静态数据,不适用于动态数据集.因而,设计一种能够处理动态流动性数据的聚类算法成为当前聚类分析领域的一个重要挑战.近年来在不同的应用领域,大量的研究已经应用增量聚类算法解决部分具体的实际问题,如异常检测[3,4],高维数据处理[5],隐私数据的增量聚类[6],基因表达数据聚类[7]等.
近年来,对大数据有效信息的获取需求越来越高,增量式方法在数据挖掘中尤其是在聚类分析中变得非常流行,解决动态数据集的聚类逐渐成为一个新的研究方向.如今,研究者们已经提出了一些增量聚类算法,Zhang C[8]等学者提出一种基于三支决策的增量聚类框架,通过基于代表点的新搜索树,在数据增加时用增量方式调整先前的聚类结果已得到新的聚类结果.Bigdeli E[9]等提出了一种增量聚类的新方法,该方法以高斯混合矩阵(GMM)的形式保存类簇信息,通过引入核心点的概念自动确定类簇数目,然后对新的数据集整体进行聚类,并通过采用核心点和GMM的概念,以原有的GMM的相似性信息标记了新的GMM矩阵.
不过上述的增量聚类研究都是基于数据对象增加而出现的,目前针对属性向量增长的研究相对较少.属性就是概念的内涵,是针对对象不同角度的认识.在实际生活中第一次观察某一对象,并不能得到其全部的信息,随着研究的深入,对于该对象不同方向的认识会更加的清晰,对于这种对象属性增长的情况,目前并没有很好的方法对其进行处理.
基于这样的一个问题,随着人工智能的兴起,粒计算在数据挖掘领域应用越来越多,专家学者们也就发现了粒计算与聚类分析之间的相关关系[10].我们将每一个属性看作一个粒,而粒度就是取不同个数的属性集,也就是说,将原来的“粗粒度”,即个数较多的属性集分割成为若干“细粒度”,或者把若干个数较少的属性合并成一个“粗粒度”对象,进行研究.由此将粒计算的思想应用到聚类算法当中产生了一种新的粒度聚类算法,这类算法利用粒度的思想更容易地获取信息,成为解决不确定性数据聚类的一个解决方案.在近年来,有关粒度聚类算法的研究论文层出不穷,主要应用于图像处理[11]、生物学中的进化计算[12]、web页面文本聚类[13]等众多领域.
数据的井喷导致单纯的粒度计算已经不能对数据进行有效地挖掘,有些学者开始考虑将多个粒度的思想与聚类算法相结合来处理问题.Zhang H B[14]等学者提出了基于随机投影的三支k-medoids动态聚类算法.该算法结合多粒度思想,利用动态随机投影三支聚类模型对高维数据进行处理,最后针对基于随机投影的三支k-medoids动态聚类算法在相应的数据集上进行验证.Xu J[15]等学者提出了一种基于密度峰值的层次聚类方法(DenPEHC),该方法在每个粒度层上都能生成一个聚类结果,通过构建网格粒度框架,使得DenPEHC能够对大规模和高维(LSHD)数据集进行聚类.
随着大数据时代的来临,数据和环境无时无刻不在发生变化,传统的粒度聚类算法,其往往只能适用于静态数据集的聚类,在处理动态的增量数据时将造成前期聚类结果可靠性的丧失,而如果重新进行聚类必然会造成效率低下和计算资源的急速增长[16].而动态的增量聚类方法对于数据的横向性增长研究比较少,即随着研究的深入对于对象的认识更清晰,对象的属性增加的问题的研究现在比较少.
本文以粒计算等处理不确定性问题的方法,提出一种多粒度增量属性的聚类方法对数据属性增长的聚类问题进行求解.本方法利用密度峰值算法[17]针对初始数据集进行处理,通过尾插法将增加属性粒集合对应的加入初始属性粒集合尾部融合成一个全新的粒度,以整合不同的粒子层上的信息,在不重复聚类为前提下以融合后的粒度层为基础,利用邻域的思想动态地更新原有的结果,进而得到增量聚类的结果.实验结果表明该方法是有效的.
2 相关定义
2.1 粒度关系
设有n个待聚类数据对象,每个数据对象由l个属性粒来表示,根据实时数据构造矩阵:
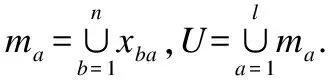
显而易见,不同的粒可能具有不同的量纲,因此需要对属性粒进行归一化处理,相应的计算公式,如公式(1)所示:
(1)
其中i∈[1,n],j∈[1,l].
粒度层gi为数据集部分属性粒的集合即:
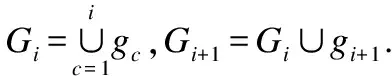
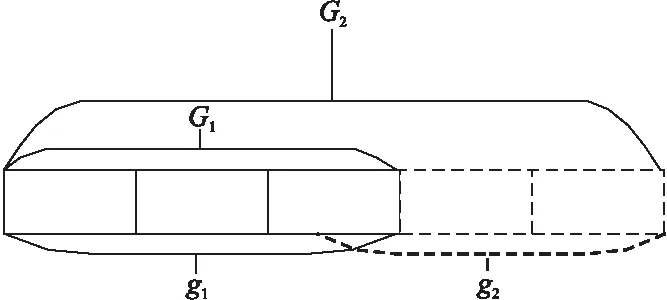
图1 粒度关系Fig.1 Granular relationship
如图1所示,在粒度的增量过程中,g1∩g2不一定为,因为在生活中对于对象的认识,第二次也出现与第一次相同的认知是很正常的.
2.2 算法流程
本文提出的多粒度增量属性聚类方法流程如图2所示.
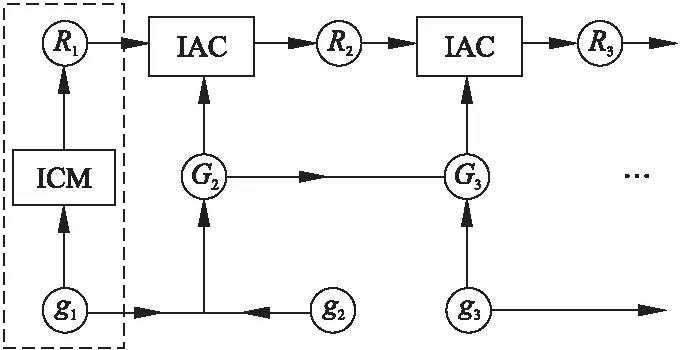
图2 多粒度增量属性聚类算法Fig.2 Multi-Granular incremental attribute clustering method
如图2中所示,本文的多粒度增量属性聚类方法首先利用初始聚类算法(初始聚类算法(ICM)详细描述在2.1节)将初始的粒度g1进行聚类(矩形虚线部分),得到初始结果R1;然后对于某一时刻新增加的属性集合g2,首先与原有的属性粒集合g1利用尾插法进行融合,得到新粒度G2;最后利用增量聚类方法(增量聚类算法(IAC)详细描述在2.2节)动态的更新原有结果R1,得到增量结果R2,以此迭代,直至未有新属性粒的加入.
算法1.多粒度增量属性聚类方法(Multi-Granularity Incremental Attribute Clustering Method,MGIAC)
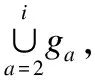
输出:聚类精度Accs,聚类结果Rs.
①R1←ICM;/*初始聚类算法(ICM)在2.1节详细介绍*/
② for eachgado
③Ra←IAC;/*增量聚类算法(IAC)在2.2节详细介绍*/
④Acca(Ra);/*计算聚类精度*/
⑤ end for
⑥ 判断是否有新粒度(gi+1)的加入,若没有则输出最后一次聚类结果Rs,Accs;
3 多粒度增量属性聚类方法
人们在分析问题时往往从不同的角度、不同的层次触发,其主要是大脑在多次处理同一问题时,随着时间环境等变化,会自行的分析并利用经验和专业知识去刻画与对象与之相应的认识,即每一次看待同一个问题,在上一次认识的基础上都可能出现新的发现.
表1 本文中的符号
Table 1 Symbols

符号含义U整个数据集mi第i个属性粒Gi第i次迭代用于聚类的粒度集合gi第i次迭代中增加的粒度集合Ri第i次的聚类结果Rs最终的结果N邻域选取个数Acci第i次的聚类精度Dimension 1初始聚类属性粒的个数ΔDimension i第i次增量聚类增加的属性粒个数
本文所提出的多粒度增量属性聚类算法分为两个部分:第一部分为初始聚类(图2中矩形虚线部分),主要采用密度峰值聚类算法[17]得到初始聚类结果;第二部分则是增量属性聚类,即针对某一时刻增加的新属性粒在不重新聚类的前提下,利用邻域思想动态更改原有结果.(密度峰值聚类的计算方法请参见文献[17])本文中出现的符号如表1所示.
3.1 初始聚类
在本文中初始聚类文献[17]提出的密度峰值聚类算法.
算法2.初始聚类算法(Initial clustering method,ICM)
输入:初始属性粒g1,截断距离dc,对象个数Num;
输出:聚类结果R1.
①Normalization(g1);/*将g1矩阵按公式(1)归一化*/
②R1←DPC;/*利用密度峰值聚类[17](DPC)输出初始聚类结果*/
3.2 增量属性聚类
在实际生活中,人们对于不同事物的认识,往往是渐进式的,首先是对于一个对象的模糊刻画,然后随着时间和环境的改变,出现了不同方面的认知,使得对象的认识更加的清晰,即人类认知不是机械的掌握一个粒度上,而是通过对每个粒度的信息的掌握,以多粒度的处理方式将信息进行细化、更新,达到了对事物的结构化认识.同时长期与你生活的人,往往在很多地方有着相似性,例如从事的职业或者生活习惯等,那么在对于外界而言,可以把你们认为是同一类人,由此我们将这两种思想,借鉴到我们的增量属性聚类算法中.
在这项工作中,随着时间或环境的变化,在某一时刻出现了新的属性粒集合gi,考虑到属性粒存在不同的量纲,首先将gi归一化,然后将gi矩阵每个对象对应的行加入到Gi-1矩阵的尾部,融合形成新的粒度Gi(如图3所示).
利用公式(2)计算Gi矩阵里对象之间的欧式距离:
(2)
然后统计对象xa(a∈[1,n])的邻域,找寻距离最近的N个对象,在原有的聚类结果Ri-1中查询这N个对象的类簇归属,寻找包含对象最多的类簇,则i属于该类簇.例如图4所示xa的邻域,当N=5时则离xa最近5邻居点为x1,x2,x3,x4,x5,其中有x1,x2,x3这3个对象在原有结果中属于类簇1,x4,x5这2个对象在原有结果中属于类簇2,那么对象xa属于类簇1.

图3 粒度融合Fig.3 Granular fusion

图4 xa的邻域Fig.4 xa neighborhood
算法3.增量属性聚类算法(Incremental attribute clustering method,IAC)
输入:原始粒度层Gi-1,增量粒度层gi,初始结果Ri-1,对象个数Num,邻域选取个数N;
输出:聚类精度Acci,聚类结果Ri.
①gi←Normalization(gi);/*将gi矩阵按公式(1)归一化*/
②Gi←Inc_set(Gi-1,gi);/*将gi中的粒对应的加到Gi-1矩阵里面生成全新的Gi*/
③ for each object do
④Di←Distance(p,q);/*计算Gi矩阵中对象间相互距离*/
⑤ end for
⑥ for each object do
⑦Neighbor(p,N);/*统计p邻域中与其距离最近的N个点*/
⑧Ri(p)←Inc_cluster(p);/*根据Ri-1,统计邻域中N个对象的类簇归属情况,选择包含对象最多的类簇,则p属于该类簇,将其输出*/
⑨ end for
4 实验分析
本文的算法采用C++语言并在工具Visual Studio 2012上实现,所有实验都在内存为8G RAM、CPU频率为2.70GHz计算机上运行.
在本节中,在UCI上的一些真实数据集验证了本文提出的方法.表2给出了关于数据集的信息.Iris1数据集是鸢尾花卉的4个属性所构成的.Lsvt Voice2是牛津大学的Athanasios
1http://archive.ics.uci.edu/ml/datasets/Iris
2http://archive.ics.uci.edu/ml/datasets/LSVT+Voice+Rehabilitation
Tsanas为帮助帕金森病人的康复将126个持续元音/a/音的特征描述为310个发声困难度.Spectf Heart3数据集描述通过计算机断层摄影对267位患者的心脏单质子的观察,针对每位患者总结出44个连续的特征.Mice Protein4数据集由77个蛋白质特征组成,有38只对照小鼠和34只三体小鼠(唐氏综合征),共72只小鼠.该数据集每个蛋白质总共包含1080个测量值,然后将缺省值的对象删除后得到552个测量值.Contraceptive5数据集是1987年印度尼西亚避孕方法调查的一部分.
表2 UCI数据集
Table 2 UCI data sets

Data setsSizeDimensionClustersIris115043Lsvt Voice21263102Spectf Heart3267442Mice Protein4552778Contraceptive5147393
如表3所示,以Iris为例,首先利用密度峰值聚类算法[17]对初次粒度层(Dimension1)进行聚类,得到了初始结果以及相应的聚类精度Acc1,以及运行时间Time1(MGIAC),然后进行方法的第二部分增量属性算法,增加粒度层ΔDimension2与原有的粒度层结合,然后对新的多粒度层进行聚类(每次增加粒的数量与数据集属性的个数有关,如Lsvt第二次增加了10个属性粒,而Iris第二次增加了1个属性粒),得到相应的聚类精度Acc2,以及增量聚类相应的运行时间Time2(MGIAC),由表3所示,没有新的粒度加入,则该算法结束.
如表3中所示,Time(MGIAC)表示本文的多粒度增量属性聚类算法从初始聚类然后经过一次或数次增量属性聚类的有运行时间,而Time(DPC)则是利用密度峰值算法对应增加属性次数的重复聚类所相加的时间(如Iris的Time(DPC)为利用密度峰值聚类算法重复聚类两次的时间).从表3中数据得本文提出的多粒度增量属性聚类算法的时间优于密度峰值聚类时间(Time(MGIAC) 对于Iris、Lvst、Heart、Contraceptive这4个数据集,由表3可得本文的多粒度增量属性的聚类方法其聚类精度Acc(MGIAC)略优于完整数据集在密度峰值聚类算法计算下的聚类精度Acc(DPC).其中我们认为,Mice Protein数据集偏差的原因在于该数据集每个对象间的距离比较接近,并且类簇相对较多,使得本文方法的聚类结果较差. 表3 实验结果 Data setsAcciDimensioniTimei(MGIAC)Timei(DPC)Acc(MGIAC)Acc(DPC)Time(MGIAC)Time(DPC)IrisDimension 1ΔDimension 20.880.903139ms32ms39ms41ms0.90.971ms80msLsvt VoiceDimension 10.39227057ms57msΔDimension 20.4111049ms60msΔDimension 30.6672050ms61msΔDimension 40.6671051ms62ms0.6670.589207ms240msSpectf HeartDimension 10.82336187ms187msΔDimension20.8363155ms190msΔDimension 30.8923157ms192msΔDimension 40.9062159ms197ms0.9060.897656ms765msMice ProteinDimension 10.35756670ms670msΔDimension20.2816567ms690msΔDimension 30.2206573ms710msΔDimension 40.2216610ms730ms0.2210.3972420ms2800msContraceptiveDimension 10.3937930ms930msΔDimension 20.4081872ms1052msΔDimension 30.4271885ms1068ms0.4270.3942687ms3076ms 在生活中,对于事物的发现都是渐进式的.很多时候,第一次的观察往往不能完全的描述出事物的特性,而第二次观察一般不会抛弃第一次观察出现的特性,其都是建立在第一次基础上来做出评价的.针对对象数目未改变,而描述对象的粒随着环境与时间的出现递增的研究,目前涉及的比较少.因此本文针对这样属性增长的情况,提出了一种多粒度增量属性的聚类方法,与一般增量聚类方法不同,该方法针对属性粒增长的情况,通过对邻域对象类簇归属的统计,以此推测增量后对象的类簇归属.本文的方法在UCI上的真实数据集得到了验证,实验结果表明本文的方法对于处理属性增长的问题具有一定的效果;但是该方法处理类簇数比较多的数据集时效果不太好,所以接下来,该方法中还需要进一步的完善,以便于更好的处理增量属性聚类的问题. 3http://archive.ics.uci.edu/ml/datasets/SPECTF+Heart 4http://archive.ics.uci.edu/ml/datasets/Mice+Protein+Expression 5http://archive.ics.uci.edu/ml/datasets/Contraceptive+Method+Choice
Table 3 Experimental results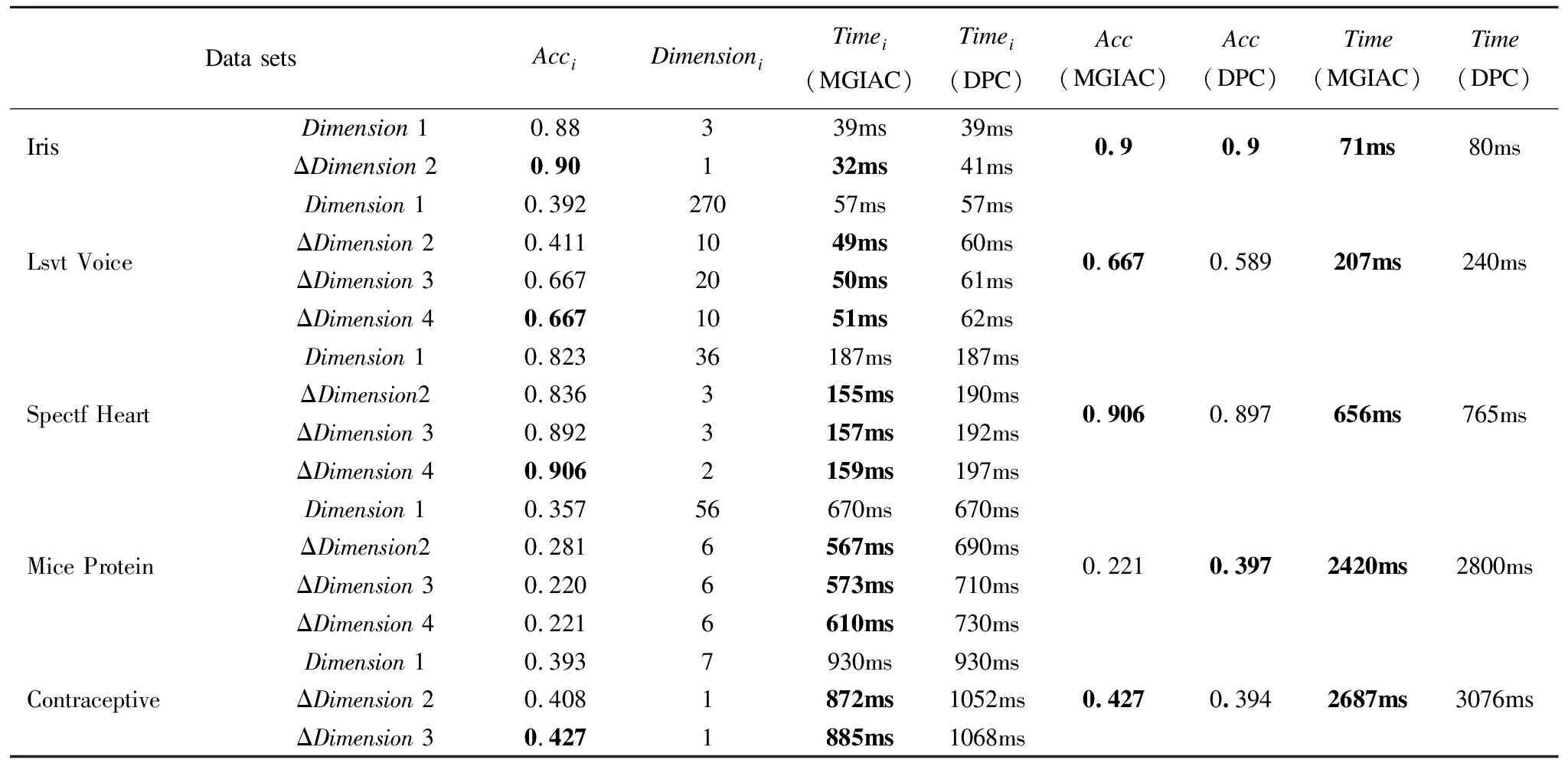
5 总 结
