复合材料板簧非线性迟滞建模和参数识别

史文库 刘鹤龙 刘巧斌 陈志勇 闵海涛

摘要：为了描述和预测复合材料板簧的非线性迟滞特性，通过动力学分析，将滞回力分解为弹性力、阻尼力和残余非线性力三部分组成，分别建立复合材料板簧的线性和非线性滞回力模型。进行复合材料板簧变频和变幅激励下的台架试验，以模型计算和试验数据的均方根误差为适应度函数，引入与迭代次数相关的非线性递减权重系数，对萤火虫算法进行改进，并与标准遗传算法（GA）、标准模拟退火算法（SA）、标准萤火虫算法（FA）进行比较，验证了所提出的改进萤火虫算法（MFA）具有相对高的精度和效率。将参数识别的结果分别代入线性模型和非线性模型，通过与试验数据的对比，说明了非线性模型具有更好的适用性，为复合材料板簧的整车性能匹配和动力学分析奠定了基础。

关键词：迟滞非线性;复合材料板簧;改进萤火虫算法;台架试验;幅变特性

中图分类号：0322; U463.33+4

文献标志码：A

文章编号：1004-4523 （2019） 06-1050-10

DOI：10. 16 385/j. cnki. issn. 1004-4523. 2019. 06. 014

引言

节能与环保的要求日益苛刻，使得汽车轻量化技术受到了广泛的关注，而复合材料在汽车轻量化应用上表现出了巨大的潜力，对复合材料在汽车上的应用进行深入的研究具有重要的工程价值。复合材料板簧是复合材料在汽车轻量化领域的一个应用，与传统的钢板弹簧相比，复合材料板簧在降低质量节省材料的同时，也降低了汽车的非簧载质量。非簧载质量的减小有助于减小车轮的动载荷，减小了车轮由于动载荷的作用而抓地能力下降的风险。因此，轻质的复合材料板簧的使用不仅可以提升汽车的燃油经济性，同时也增加了汽车的行驶安全性。

国内外学者对复合材料板簧进行了大量的研究。主要研究集中于结构参数的优化[12]、刚度和强度的有限元分析[3-5]、制造工艺[6-7]、刚度计算理论[8-11]、疲劳损伤分析与优化[12-17]等方面。现有的研究对于复合材料板簧的迟滞特性研究的较少，而其迟滞模型在整车性能仿真方面不可或缺。因此，建立简洁、高效的迟滞特性模型对复合材料板簧的迟滞特性进行仿真分析具有重要的意义。

传统的钢板弹簧迟滞非线性模型有：SAE三连杆模型[18]、有限元模型[19]、Fancher模型[20]和Bou-W en模型[21]等。復合材料是一种具有黏弹性非线性特征的材料，其迟滞特性与传统的钢板弹簧一样具有幅变和频变等特征，而上述模型对于复合材料板簧迟滞特性的建模是否适用，是否存在更简洁实用的模型可以用于复合材料板簧的迟滞特性建模将是本文研究的一个重点。另一方面，在非线性迟滞模型的参数识别方法上，已有的研究集中于进化算法[22]、多目标遗传算法[23]、粒子群算法[24]、人工神经网络算法[25]、非线性状态空间方法[26]、马尔科夫链蒙特卡洛方法[27]等方法，由此可见，智能算法在非线性模型的参数识别方面展示出了极大的优势，因此探索新型智能启发式算法在非线性迟滞模型参数识别方面的应用是本文的另一个重点。

结合国内外研究背景和课题组前期的相关研究成果，本文在分析目前迟滞非线性建模及模型参数识别的基础上，提出一种简洁的非线性模型用于模拟复合材料板簧的迟滞非线性，并根据试验测得的迟滞曲线，采用改进的萤火虫算法对模型的参数进行识别。

合材料板簧台架试验

本文所研究的复合材料板簧为E玻璃纤维一聚氨酯基复合材料制作而成，采用单片抛物线结构，复合材料板簧的样件如图1所示。对复合材料板簧样件进行台架试验，分别测试不同力激励幅值和不同激励频率下的力一位移滞回曲线。试验台架如图2所示。试验时，预载力为11600 N。激励频率为0. 5-3 Hz，每隔0.5 Hz测取一组数据，共6组不同位移激励幅值。最小力加载幅值为700 N，最大加载幅值为3500 N，每隔700 N测量一组数据，共5组数据。因此，本次试验共采集到不同力加载幅值和不同激励频率下的数据共3 0组。

图3所示为0.5 Hz激励频率下不同力加载幅值的滞回曲线，由图可知随着力激励幅值的增加，滞回曲线产生明显的变化，加载/卸载过程的力所形成的封闭曲线包围的面积加大。

图4所示是在700 N力加载幅值的条件下，不同激励频率下的复合材料板簧滞回曲线，由图可知，在试验频率范围内，其滞回曲线变化不明显。因此，为了简化研究，在后文的研究中，忽略频率对复合材料板簧滞回特性的影响，仅考虑力幅值对滞回特性的影响。

2 复合材料板簧迟滞特性建模

2.1 线性模型

复合材料板簧在受到外界载荷作用时，发生形变，产生回复力，回复力中的一部分与外界激励的位移相关，将这一部分回复力定义为弹性力，另一部分与外界激励的速度相关，将这一部分回复力定义为阻尼力，可以获得如下式所示的复合材料板簧线性迟滞模型。

F =k（A，f）z+c（A，f）x+F。

（1）式中 x为位移激励，x为位移激励的导数，即速度，A为激励力幅值，厂为激励频率，k（A，f）为弹性刚度系数，c（A，f）为阻尼系数，F0为预载荷，在线性模型中，假定F0为常数。

复合材料板簧用于支撑汽车的簧载质量，而汽车簧载质量的偏频在1-2 Hz以内，因此，在进行复合材料板簧台架试验时，激励频率范围取0. 5-3Hz。由复合材料板簧台架试验可知，在所研究的激励频率范围内，频率对复合材料的滞回特性的影响很小，为了研究的方便，忽略复合材料板簧滞回特性的频变特性，将式（1）简化为如下式所示

F =k（A）x-+ c（A）x+F0（2）

对于每一个力振幅激励下的滞回曲线，线性滞回模型存在2个未知参数，即k和e。

2.2 非线性模型

根据矢量的可叠加性，对式（2）的线性滞回模型进一步完善，引入残余非线性项Fr，建立复合材料板簧的非线性滞回特性模型，如下式

F =k（A）x-+ c（A）x-+Fr（x，x，A）

（3）式中 Fr（x，x，A）为残余非线性力，是位移、速度和振幅的非线性函数，对于大黏弹性系统，可用Bouc-W en模型等方法对残余非线性力进行拟合，而Bouc-Wen模型的参数较多，且参数识别的初始值不容易确定。故本文在经过对线性模型拟合后的残余项进行分析发现，对于本文所研究的复合材料板簧，其滞回力的非线性残余项可表示为预载力的倍数δ（A），即

Fr（x，x，A）=δ（A）F0（4）

将式（4）代人式（3），可得

F =k（A）x+c（A）x十δ（A）Fo0（5）

对于每一个力振幅激励下的滞回曲线，非线性滞回模型存在3个未知参数，即k，c和δ。

2.3 模型参数影响分析

为分析滞回特性模型的关键参数对滞回环的影响，分别对k，c和δ这3个参数进行影响分析。分析中，3个参数的初始值分别为k0，C0和δ0，参数影响分析采用控制变量法，固定2个参数，每次只改变1个参数值。图5所示是刚度参数k对滞回特性的影响，由图可知，随着刚度的加大，滞后曲线整体斜率增大;图6所示是阻尼参数c对滞回特性的影响，由图可知，随着阻尼的增大，滞回环所占面积增大，表示复合材料板簧在加载和卸载过程中的能量损耗增加。

图7所示是残余力系数δ对滞回环的影响，由图可知，随着残余力系数的增大，滞回环整体延y轴下移，应该指出的是非线性残余力系数δ中包含了非线性弹性力、非线性阻尼力、预载力和回复力测量误差等几个部分，而δ（A）仅是在数值上将非线性残余力等效为预载力的倍数，因此图7的分析并不能完全体现非线性模型中δ（A）对曲线的影响，由于上述非线性弹性力和非线性阻尼力的存在，δ（A）必然对滞回环的斜率和包围面积有影响。

3 基于改进的萤火虫算法的参数识别

参数识别是迟滞特性建模的核心之一，其精度和效率直接关系到建模的成败。现有的非线性最小二乘法等传统算法用于参数识别常有初始值不易确定、收敛速度慢和目标函数确定困难等弊端。新兴的智能算法在非线性参数识别领域展现了巨大的潜力，各种算法不断涌现，算法的适用性在解决实际工程问题中不断得到验证，各算法也针对不同的问题得到了不断的改进和完善。本文尝试将萤火虫算法这种智能算法用于所提出的非线性迟滞模型的参数识别，并有针对性的对算法进行了改进，在提升了算法收敛精度的同时，保证了算法的运行效率。为验证改进的萤火虫算法的相对优越性，将改进的萤火虫算法与遗传算法、模拟退火算法这两种相对成熟的智能算法比较;另外，也与改进前的萤火虫算法做了比较。

3.1 参数初始值和取值范围的确定

采用人工智能算法进行参数识别时，参数的初始值和取值范围关系到参数识别的效率和精度，合适的初始值和取值范围可大幅提升参数识别结果的可信度，减小参数识别的时间成本。对于非线性和线性模型中涉及到的3个参数k，c和δ，k的初始值设为滞回特性曲线一次线性回归结果的斜率，如图8所示，即k0=130 N/mm。c的初始值根据下式计算式中 △E为滞后环所包围的面积，E为加载过程所包围曲线的面积，这两个面积表征的是能量，f为位移激励的频率。

为分析方便，取最小激励振幅下的滞回环，即700 N力激励下的位移一力滞回曲线表征的阻尼值为初始值，通过计算得到c0=5 N·s/mm。通过分析各组不同振幅下的试验数据，发现非线性残余力与预载力基本相当，故将非线性残余项系数δ的初始值设为δ0=1。

各参数的取值范围为

3.2 改进萤火虫算法

萤火虫算法（Firefly Algorithm，FA）是2 008年由剑桥大学学者Yang Xinshe所提出的一种新型启发式群智能优化算法[28-30]，其基本思想借鉴了萤火虫通过发光而实现信息沟通的功能。通过发光的随机粒子之间距离的迭代计算从而实现函数寻优。

从数学的角度对萤火虫算法相关概念的定义如下：

萤火虫的亮度定义如下式

I（rij）=I0e-rr2j

（8）式中 IO为萤火虫的初始亮度，γ为光强吸收系数，rij为第i个和第j个萤火虫之间的笛卡尔距离，如下式所示式中 xi和xi分别为第i和j個萤火虫的坐标，d为坐标的维度。

萤火虫之间的吸引度定义如下式所示

β=β0e-yr2ij

（1 0）式中 β0为萤火虫的初始吸引度。

亮度较小的萤火虫朝较亮萤火虫的位置移动的位置更新公式如下式所示

xi（t+1）=xi（t） +β（Xi （t） -xj （t））+

a（rand-0.5）

（11）式中 t为迭代次数，a为步长因子，rand为O到1之间的随机数。

式（11）的位置更新迭代过程中，容易出现早熟而陷入局部最优，且在迭代后期萤火虫聚集在最优点附近，萤火虫之间的吸引力过大，可能导致解的震荡。为解决以上问题，学者们提出了很多种改进方法[31-39]，这些方法实现的目的就是在保证算法的全局搜索能力的同时，提升算法的局部寻优能力，希望在迭代初期，算法具有较强的全局搜索能力，而在迭代后期，算法具有较强的局部搜索能力。现有文献报道中对萤火虫算法的改进基本都是线性递减权重的，很少有非线性递减权重的报道，本文根据所优化问题的特性，经过大量的测试，发现使用1/2次根值递减的权重可实现更好的优化效果。

改进后的位置更新公式如下式

xi（t+1）=φ（t）xi（t）+β（xi（t）-xi（t））+

a（rand-0.5）

（12）式中 φ（t）为萤火虫当前迭代位置的权重，与迭代次数成非线性递减关系，如下式所示

由式（13）获得的权重随迭代过程的变化曲线如图9所示。由图可知，在迭代的初始阶段，权重φ（t）较大，这保证了初始迭代时算法的全局寻优能力，而在迭代的终了阶段，权重φ（t）较小，这保证了算法在后期的局部搜索能力。

3.3 适应度函数的确定

将适应度函数定义为模型计算的回复力Fsi与试验测得的回复力F矗之间相对误差平方和的均值，即如下式所示的均方误差（RootMean Square Er-ror，RMSE）式中 X为待识别的参数变量，n为参与识别的样本点总数，i为样本点序号。参数识别的目的是在可行域内获得一组使得目标函数值最大（RMSE最小）的变量。

4 参数识别结果与讨论

4.1 改进萤火虫算法参数识别的优点

为验证所提出的算法进行参数识别的优越性，分别采用改进萤火虫算法（MFA）、标准遗传算法（GA）、标准模拟退火算法（SA）、和标准萤火虫算法（FA）进行0.7 kN激励力幅值T的非线性滞回力模型的3个关键参数识别。4种算法的种群数量统一设置为30，最大迭代步数为80。萤火虫算法和标准萤火虫算法的初始亮度I0=1，初始吸引度β0=1，步长因子a=0.5，光强吸收系数r设为0.9。标准遗传算法的交叉概率为0.7，变异概率为0.1，采取轮盘赌法选择机制。模拟退火算法的参数设置按照MATLAB最优化工具箱的默认设置。

分别记录以上4种算法的运行时间和最终适应度值，如表1所示。由表可知，模拟退火算法在运行时间上略有优势，但是其优化效果较差。标准遗传算法和标准萤火虫算法在优化效果上相近，标准萤火虫算法的运行时间稍长，而经过改进后的萤火虫算法，无论在求解精度上，还是在运行效率上，都得到了一定的提升，其优化精度优于标准遗传算法，均方根误差控制在1%以内，且运行效率略高于标准遗传算法。

图1 0所示是这4种算法随迭代次数的收敛曲线，由图可以直观地看出各种算法的精度和效率。由图可知，改进以后的萤火虫算法的精度最高，改进后的萤火虫算法在初始迭代阶段，其适应度函数呈现了阶梯状的上升，而标准粒子群算法出现了早熟，因而陷入局部最优。

4.2 参数识别最终结果

在验证了改进萤火虫算法的优越性后，采用改进的萤火虫算法分别对各力振幅激励下的线性滞回曲线和非线性滞回曲线进行参数识别。

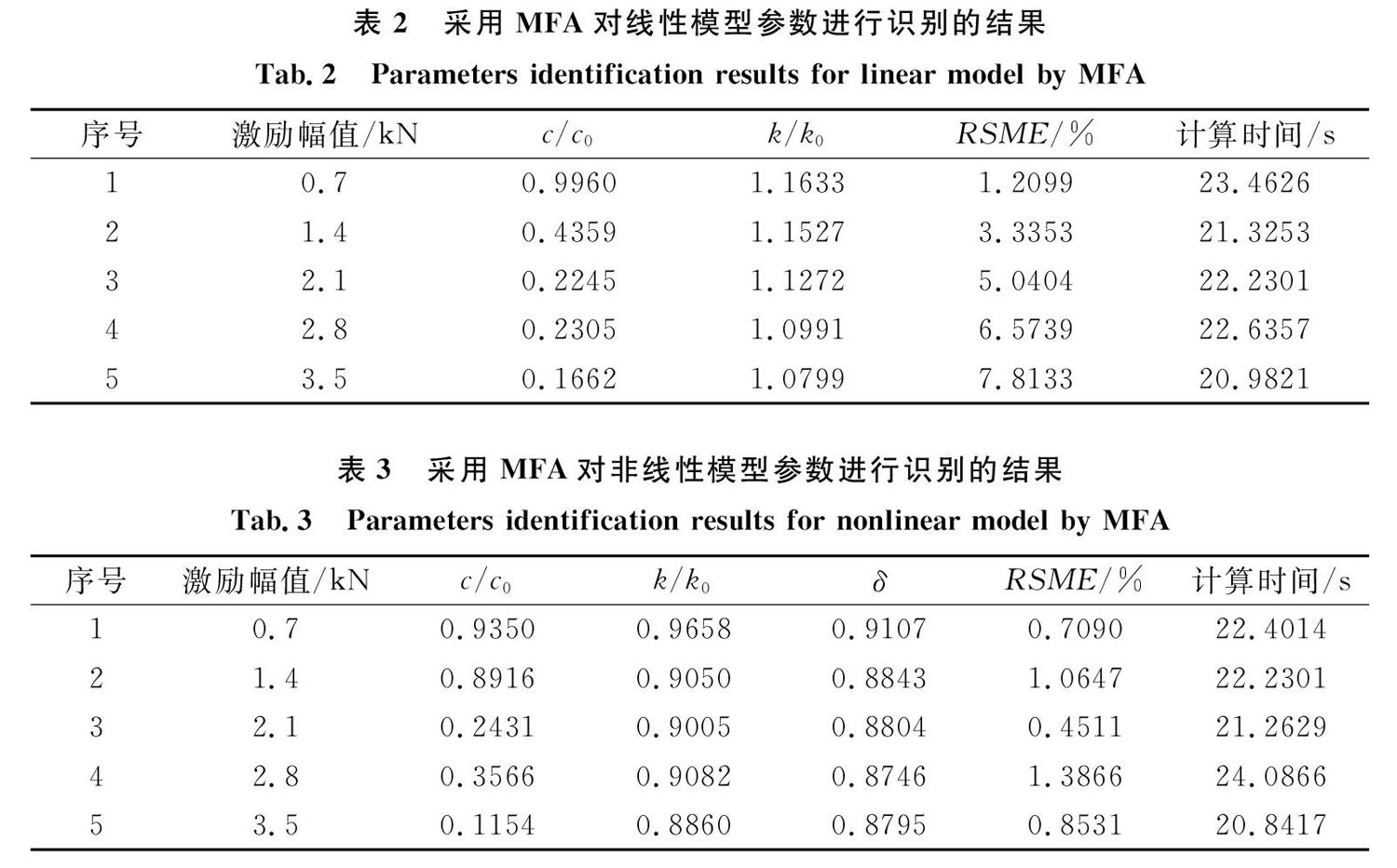
表2和3分别为采用改进的萤火虫算法对不同力载荷下的线性模型和非线性模型的参数进行识别的结果。由表2可知，随着力激励幅值的增加，线性模型的误差逐渐增大，而线性模型的等效刚度和阻尼略有减小。对比表2和3的结果可知，采用非线性模型后，滞回力的平均预测误差的最大值从7. 8133%下降到1.3866%，而参数识别的时间基本不变。说明引入非线性残余力项可以大大提高模型的精度。图11所示是不同预载力下的位移一滞回力和时间一滞回力曲线。由图可知，非线性模型与实测数据吻合的很好，而线性模型误差较大，且激励力幅值越大，线性模型的误差也越大，说明大幅值的激励力增大了复合材料板簧的非线性。

在验证了本文所提出的非线性滞回模型的准确性的基础上，进一步对非线性模型中3个参数的幅变特性进行分析，发现使用二次多项式可以实现这3个参数的良好拟合，下式是拟合结果

图12 -14所示，分别是刚度k，阻尼c和非线性残余力系数δ的二次多项式拟合结果和基于改进的萤火虫算法参数识别结果的对比。由图可知，随着力振幅的增大，复合材料板簧的滞回模型中的刚度、阻尼和非线性残余项均有所下降，说明随着力振幅的增大，板簧的非线性增加，耗散能量增加。

5 结 论

本文在分析复合材料板簧滞回力物理意义的基础上，将滞回力分解为线性弹性力、线性阻尼力和非线性残余力三部分，建立起了复合材料板簧滞回力的非线性模型，并采用改进萤火虫算法对非线性模型中的模型参数进行识别，将识别结果与线性模型和实测结果对比，验证了所提出的非线性模型具有很好的适用性，且参数识别方法具有相对较高的效率和精度。主要结论如下：

（1）复合材料板簧的滞回力存在非线性因素，其滞回特性的幅变特性明显，而频变特性不明显，采用线性模型对滞回力进行拟合的误差较大;

（2）采用本文所提出的非线性滞回力模型可以较好地描述和预测复合材料板簧的滞回特性，且效率和建模精度都相對较高;

（3）通过位置坐标权重非线性改进后的萤火虫算法参数识别方法，与经典萤火虫算法、经典粒子群算法和经典遗传算法相比，具有更好的精度和相对较高的效率，可以为相关非线性模型的参数识别提供参考;

（4）进一步的研究要通过对复合材料板簧的弹塑性力学机理进行深入的探索，分析滞回特性中的非线性残余项与位移和速度等物理量的关系;另一方面，采用不同的参数识别方法对模型的参数进行识别，以进一步提高参数识别的效率和精度。

参考文献：

[1] Rajendran I， Vijayarangan S.Optimal design of acomposite leaf spring using genetic algorithms[J].Computers & Structures， 2001， 79（11）：1121-1129.

[2] Sancaktar E，Gratton M. Design， analysis， and opti-mization of composite leaf springs for light vehicle ap-plications[J]. Composite Structures， 1999， 44（2-3）：195-204.

[3] Mithari R，Patil A， Aitavade E N.Analysis of com-posite leaf spring by using analytical&FEA[J]. In-ternational Journal of Engineering Science & Technol-ogy， 2012， 4（12）：4809-4814.

[4] Shokrieh M M， Rezaei D.Analysis and optimization ofa composite leaf spring[J]. Composite Structures，2003， 60（3）：317-325.

[5] Hou J P，Cherruault J Y， Nairne I，et al.Evolution ofthe eye-end design of a composite leaf spring for heavyaxle loads[J]. Composite Structures， 2007， 78（3）：3 51- 358.

[6] Banka H， Muluka R，Reddy V. Fabrication and experi-mental analysis of epoxy-glass fiber composite leaf spring[R]. SAE Technical Paper Series， 2017-28-1985.

[7]Rai V， Saxena G. Development of a composite leafspring for a light commercial vehicle （Tata Magic）[J].International Journal of Engineering Research& Ap-plications， 2013， 3（5） ：110-114.

[8]Jadhao K K， Dalu D R S. Experimental investigation& numerical analysis of composite leaf spring[J]. In-ternational Journal of Engineering Science& Technol-ogy， 2011， 3（6） ：445-477.

[9] Shankar G S S， Vijayarangan S. Mono composite leafspring for light vehicle-design， end joint analysis andtesting[J]. Materials Science， 2006， 12（3） ：220-225.

[10] Azzam B S N， Mokhtar M O A， Naga S A R. Theo-retical and numerical analysis of fibrous composite C-springs[R]. SAE Technical Paper Series， # 2001-01-2 710.

[11] Shi W， Qian C， Chen Z， et al. Establishment of theo-retical model of composite leaf springs by using themechanics of composite materials[J]. Journal of Rein-forced Plastics& Composites， 2017， 36（18）：1316-1326.

[12] Kumar M S， Vijayarangan S. Static analysis and fa-tigue life prediction of steel and composite leaf springfor light passenger vehicles[J]. Journal of Scientific&Industrial Research， 2007， 66（2） ：128-134.

[13] Kueh J T J， Faris T. Finite element analysis on thestatic and fatigue characteristics of composite multi-leaf spring[J]. Journal of Zhejiang University-ScienceA（Applied Physics& Engineering）， 2012， 13（3）：15 9-16 4.

[14] Manjunath H N， Manjunath K， Rangaswamy T. Stat-ie analysis and fatigue life prediction of composite leafspring for a light commercial vehicle （TATA ACE）[J]. International Journal of Engineering Research，2014， 3（7） ：422-425.

[15] Shamsaei N， Rezaei D. Comparing fatigue life reliabil-ity of a composite leaf spring with a steel leaf spring[C]. ASME， Biennial Conference on Engineering Sys-tems Design and Analysis， 2004：371-374.

[16] Kumar M S， Vijayarangan S. Analytical and experi-mental studies on fatigue life prediction of steel andcomposite multi-leaf spring for light passenger vehiclesusing life data analysis[J]. Materials Science， 2007，13（2） ：141-146.

[17] Qian C， Shi W， Chen Z， et al. Fatigue reliability designof composite leaf springs based on ply scheme optimization[J]. Composite Structures， 2017， 168： 40-46.

[18]官欣，齊海政，詹军，等，基于SAE三连杆模型的钢板弹簧迟滞特性建模[J].吉林大学学报（工学版） ，2010， 40（S1） ：76-0080.

Guan X， Qi H Z， Zhan J， et al. Modeling for leafspring hysteretic characteristic based on SAE three-link model[J]. Journal of Jilin University（EngineeringEdition） ， 2010， 40（S1） ：76-0080.

[19]周孔亢 ，陆建辉 ，侯永涛 ，等.基于 RecurDyn的钢板报， 2014， 50（4） ：128-134.

Zhou Kongkang， LU Jianhui， Hou Yongtao， et al.Dynamics modeling and parameter identification of leafspring based on recurdyn[J]. Journal of MechanicalEngineering， 2014， 50（4） ：128-134.

[20] Liu X， Chen W， Zhao J， et al. Fitting precision analy-sis on the dynamic stiffness of leaf spring based on theFancher Model[J]. Automobile Technology， 2017，（3） ：38-41.

[21] Xie Q X， Zhou S Y， Zhang N， et. al. Simulation andexperimental study on Bouc-Wen hysteresis model ofleaf spring[J]. Automobile Engineering， 2016， 38（5） ：632-637.

[22] Charalampakis A E， Koumousis V K. Identification ofBouc-Wen hysteretic systems by a hybrid evolutionaryalgorithm[J]. Journal of Sound& Vibration， 2008，314（3） ：571-585.

[23] Ortiz G A， Alvarez D A， Bedoya-Ruiz D. Identifica-tion of Bouc-Wen type models using multi-objectiveoptimization algorithms[J]. Computers& Structures，2013 ， s114-115 （1） ：121-132.

[24] Charalampakis A E， Dimou C K. Identification ofBouc-Wen hysteretic systems using particle swarm op-timization[J]. Computers& Structures， 2010， 88（ 21） ：119 7-12 0 5.

[25] Xie S L， Zhang Y H， Chen C H， et al. Identificationof nonlinear hysteretic systems by artificial neural net-work[J]. Mechanical Systems& Signal Processing，2013， 34（1-2） ：76-87.

[26] Noel J P， Esfahani A F， Kerschen G， et al. A nonlin-ear state-space approach to hysteresis identification[J]. Mechanical Systems& Signal Processing， 2016，84 ：171-184.

[27] Ortiz G A， Alvarez D A， Bedoya-Ruiz D. Identifica-tion of Bouc-Wen type models using the TransitionalMarkov Chain Monte Carlo method[J]. Computers&Structures， 2015， 146：252-269.

[28] Yang X S. Firefly algorithms for multimodal optimiza-tion[J]. Mathematics， 2012， 5792：169-178.

[29] Yang X S， He X. Firefly algorithm： Recent advancesand applications[J]. International Journal of SwarmIntelligence， 2013， 1（1） ：36-50.

[30] Fister I， Jr I F， Yang X S， et al. A comprehensive re-view of firefly algorithms[J]. Swarm& EvolutionaryComputation， 2013 ， 13 （1） ：34-46.

[31] Hong CO ， Tilahun S L， Tang S S. A comparativestudy on standard， modified and chaotic firefly algo-rithms[J]. Pertanika Journal of Science& Technolo-gy， 2015， 23（2） ：251-269.

[32] Fister I， Yang X S， Brest J， et al. Modified firefly al-gorithm using quaternion epresentation [J]. ExperSystems with Applications， 2013， 40（18） ：7220-7230.

[33] Niknam T， Azizipanah-Abarghooee R， Roosta A. Re-serve constrained dynamic economic dispatch： A newfast self-adaptive modified firefly algorithm[J]. IEEESystems Journal， 2012 ，6 （4） ：635-646.

[34] Verma O P， Aggarwal D， Patodi T. Opposition and di-mensional based modified firefly algorithm[Jl. ExpertSystems with Applications， 2016， 44（C） ：168-176.

[35] Xiao L， Wang C， Liang T， et al. Combined modelbased on multiple seasonal patterns and modified fire-fly algorithm for electrical load forecasting[J]. Ap-plied Energy， 2016， 167：135-153.

[36] Li M， Zhang Y， Zeng B， et al. The modified fireflyalgorithm considering fireflies' visual range and its ap-plication in assembly sequences planning[J]. Interna-tional Journal of Advanced Manufacturing Technology，2016 ， 82 （ 5-8） ：1381-1403.

[37] Wang B， Li D X， Jiang J P， et al. A modified fireflyalgorithm based on light intensity difference[J]. Jour-nal of Combinatorial Optimization， 2016， 31（3） ：1045-10 60.

[38] Yelghi A， Kose C. A modified firefly algorithm forglobal minimum optimization[J]. Applied Soft Com-puting， 2018， 62：29-44.

[39] Sedaghati R， Hakimzadeh M， Fotoohabadi H， et al.Study of network reconfiguration in distribution sys-tems using an adaptive modified firefly algorithm[J].Automatika， 2016， 57（1） ：27-36.