基于PSO?ELM特征映射的KNN分类算法
2019-03-12丁建立刘涛王家亮曹卫东
丁建立 刘涛 王家亮 曹卫东

关键词: K近邻分类算法; 极端学习机; 特征映射; 粒子群算法; 混合算法; 线性不可分
中图分类号: TN911.1?34; TP181 文献标识码: A 文章编号: 1004?373X(2019)05?0152?05
KNN classification algorithm based on PSO?ELM feature mapping
DING Jianli1, 2, LIU Tao1, WANG Jialiang1, 2, CAO Weidong1, 2
(1. College of Computer Science and Technology, Civil Aviation University of China, Tianjin 300300, China;
2. Tianjin Key Lab for Advanced Signal Processing, Civil Aviation University of China, Tianjin 300300, China)
Abstract: The K?nearest neighbor (KNN) classification algorithm based on PSO?ELM (particle swarm optimization?extreme learning machine) feature mapping is proposed because the traditional ELM algorithm and KNN classification algorithm have some shortcomings in classification process. The input?layer weight and hidden?layer neuron of ELM algorithm are used to perform the nonlinear mapping for the input sample. The PSO algorithm is used to find a group of optimal ELM mapping parameters, and then the mapped feature sample is input into KNN algorithm, which can improve the ability to deal with the linear impartibility problem. The experimental results of several data sets show that the proposed algorithm has higher classification accuracy than improved KNN algorithm and improved ELM algorithm.
Keywords: K?nearest neighbor classification algorithm; extreme learning machine; feature mapping; particle swarm optimization algorithm; hybrid algorithm; linear impartibility
0 引 言
K近邻分类算法[1?2](K?Nearest Neighbor,KNN)是一种简单的分类算法,在数据挖掘等领域有着广泛的应用。作为一种有监督的学习算法,使用投票机制确定未知样本的类别,即给定一组有类别属性的数据作为训练样本,当有新的未知类别样本到来时,首先找到[K]个与未知样本最为接近的训练样本,在[K]个与未知样本最接近的训练样本标签中,出现次数最多的标签就是未知样本所属的类别标签。
从KNN算法的原理[3]可以总结出,该算法有两个关键因素需要考虑,即[K]值的设定和距离度量。[K]值的选取对于该算法分类的正确率有着重要作用。如果[K]值太小,则分类结果容易受到噪声样本影响;如果[K]值太大,样本数较少,类别会受到影响。其次是距离度量,常用的距离度量方法如欧氏距离和余弦距离等,不同距离度量的选择对于分类结果也产生了很大的影响。
极端学习机算法[4?7](Extreme Learning Machine,ELM)是由Huang等提出来的一种单隐层前向反馈神经网络(Single Hidden Layer Feed Forward Neural Networks,SLFN)。该算法与一般的SLFN算法相比,可以随意地选择隐层神经元数目和激活函数类型,构造不同的网络结构,隐层偏差和输入层权值可以随机产生,再利用输出层期望使用最小二乘法计算输出层权值。该算法具有计算速度快、泛化能力好等优点,避免了传统神经网络使用梯度算法计算时间长,容易陷入局部最优解的问题。目前在系统辨识、模式识别、函数逼近等方面具有广泛的应用。由于输入层权值和隐层偏差是随机生成的,该算法通常需要数目较多的神经元才能保证有较好的泛化能力和稳定性。同时由于输出层权值矩阵由隐含层输出矩阵的广义Moore?Pennose逆矩阵求出,当隐含层节点数目过多时容易出现过拟合现象,降低ELM的泛化能力。对待线性不可分的样本[8?10],使用常用的欧氏距离和余弦距离来计算样本相似程度进行分类可能会导致效果很不理想。KNN算法在处理线性不可分问题时,可能会得到很差的分类效果。为了解决这类问题,可以将样本进行特征映射,从低维特征空间映射到高维特征空间中,从而将线性不可分问题转化为线性可分问题,再使用传统的距离算法计算样本间的距离,从而提高分类正确率。
文献[11]提出ELM K?means算法,使用ELM算法进行特征映射,再将映射后的样本特征指标输入到聚类算法中,取得了良好的效果。随后文献[12]又提出基于ELM特征映射的KNN算法。上述算法在利用ELM做特征映射时都存在稳定性较差,需要大量神经元即需要映射的维度极高等缺点。
针对ELM?KNN存在的问题,本文提出使用PSO?ELM特征映射的KNN算法。该算法利用ELM的输入层权值和隐层对输入样本进行特征映射,并运用PSO算法寻找一组最优的ELM输入层权值和隐层偏差,再将映射后的样本特征指标输入到KNN算法中,提高处理分类问题的能力。
1 ELM?KNN算法
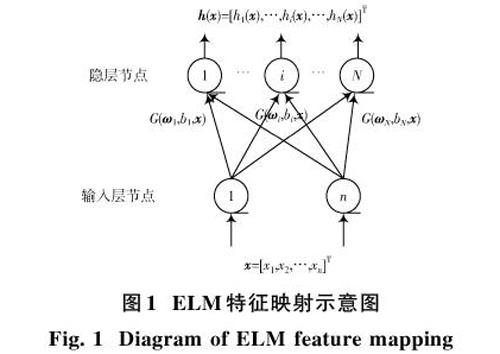
设输入样本数据为[n]维向量[x=[x1,x2,…,xn]T],通过一个ELM的输入权值和隐层神经元将[x]映射到一个[N]维的ELM特征空间(即隐层特征空间,[N]为隐层节点个数,也是新特征空间的维度),[x]在特征空间中对应的特征向量为:
[h(x)=[h1(x),h2(x),…,hN(x)]T=[G(ω1*x+b1),G(ω2*x+b2),…,G(ωN*x+bN)]T] (1)
式中:[Gωi*x+bi]为隐层节点的输出,[ωi]为连接[n]个输入节点和第[i]个隐层节点的[N]维权重向量;[bi]为第[i]个隐层节点的偏差。由于[ωi]和[bii=1,2,…,N]是随机生成的,无需计算和调整,在特征映射过程中只需要人为调整隐层节点个数,再将映射后的样本[h(x)]作为新的特征样本输入到KNN算法中,计算待分类样本所属的类别。
由于隐藏偏差和输入层权值随机生成导致ELM?KNN在计算时往往需要映射到一千维以上才能保证较高的分类和稳定性。这导致算法实用性较差,往往需要计算很多次才能得到理想的结果。
2 粒子群算法
粒子群算法[13](Particle Swarm Optimization,PSO)是一种模仿鸟类捕食行为的智能优化算法。在算法初始阶段随机生成一组随机解,然后通过一定规律迭代地寻找最优解。不同于遗传算法使用交叉以及变异寻找最优解,该算法的迭代策略是解空间朝着最优一组解空间的方向进行更新。同现行的其他智能优化算法相比,该算法具有收敛速度快,不易陷入局部最优解,算法简单,参数设置少等特点。目前PSO算法已广泛应用到如函数优化、参数估计、模型改进、模糊系统控制等众多领域。
在PSO中,每一个粒子代表空间中的一点,其对应的空间坐标代表该问题的一组解,记为[Xi=xi1,xi2,…,xiD],可以利用适应度函数计算每个粒子的适应度,同时每个粒子还有一个速度属性[Vi=vi1,vi2,…,viD],用来决定它们的方向和距离。粒子之间通过共享最优粒子的信息在解空间中搜索最优解。
粒子群首先计算每个粒子的适应度fitness,选择适应度最优的点,让其他所有点朝着最优点移动,以此迭代寻找最优解。在每次迭代过程中,粒子先朝着当前最优解更新速度,然后更新当前位置。
粒子更新速度的公式为:
[vid=vid+c1?rand(pid-xid)+c2?rand(pgd-xid)] (2)
粒子更新位置的公式为:
[xid=xid+vid] (3)
式中:[Pi=pi1,pi2,…,piD],表示第[i]个粒子的局部最优解,即第[i]个粒子每次迭代到目前为止经历过的最佳点;[Pg=pg1,pg2,…,pgD],表示所有粒子群的最优解,即目前为止粒子群所搜索到的适应度最优的解;[c1]和[c2]是学习因子,为大于零的常数;[rand]表示在[0,1]生成随机数。
3 基于PSO?ELM特征映射的KNN算法
为了改进ELM?KNN算法的不足,本文提出一种基于PSO?ELM特征映射的KNN算法。该算法利用PSO寻优策略代替ELM算法输入层权值和隐层偏差随机生成的过程。利用优化后的ELM输入层和隐层激活函数对样本进行特征映射,再将映射后的特征样本输入到KNN算法中进行分类。
从ELM算法角度,本文算法有以下几个方面的改进:
1) 本文算法利用PSO寻优策略代替了ELM算法输出层权值和隐层偏差随机生成的过程,避免了该算法输出层权值和隐层偏差随机生成导致的消耗神经元数目过多、结果稳定性差等缺点。
2) ELM算法输出层的权值是利用最小二乘法计算得到的,ELM算法在对样本进行特征映射以后只是将映射后的特征样本进行加权求和,从而计算每个样本的类别。利用KNN算法的投票机制代替这一过程,从而可以有效避免其容易出現的过拟合问题。
3) 从KNN算法的角度,对于传统KNN算法的距离度量的不足进行了改进。利用PSO?ELM进行特征映射提高了该算法处理线性不可分问题的能力。另外,特征映射的使用还能够起到消除冗余信息,提取特征信息的作用。
具体算法如下:
对于给定[n]维输入样本[x=[x1,x2,…,xn]T],首先利用粒子群算法随机生成一组输入层权值[ωi]和隐藏偏差[bi],通过具有[N]个隐层神经元、激活函数为[G(x)]的ELM对样本进行特征映射后的特征向量为:
[h(x)=[h1(x),h2(x),…,hN(x)]T=[G(ω1*x+b1),G(ω2*x+b2),…,G(ωN*x+bN)]T]
式中:[Gωi*x+bi]为隐层节点的输出,[ωi]为连接[n]个输入节点和第[i]个隐层节点的[N]维权重向量;[bi]为第[i]个隐层节点的偏差。常用的激励函数有Hardlim函数、Sigmoid函数、Sine函数等。
ELM特征映射示意图如图1所示。


再将特征变化后的[h(x)]输入到KNN算法中,计算样本分类的正确率。分类正确率计算方法如下:
[正确率=分类正确样本数样本总数×100%] (4)
将分类正确率作为适应度fitness返回给粒子群算法,作为每一个粒子的适应度。通过PSO多次迭代,获得使分类正确率最高的一组输入层权值[ωi]和隐层偏差[bi]。
算法步骤如下:
1) 随机生成粒子群,每一个粒子群的位置坐标代表ELM输入层权值[ωi]和隐层偏差[bi];
2) 依次选择各个粒子,利用式(1)对输入样本[xi] 做特征映射得到[h(x)],将[h(x)]作为新的样本输入到KNN中,并计算分类正确率作为对应粒子的适应度;
3) 根据适应度更新每一个粒子的局部最优解[Pi]和全局最优解[Pg];
4) 根据式(2)和式(3)更新每一个粒子的速度和位置;
5) 判断是否达到最大迭代次数,若达到最大迭代次数,则输出最优的粒子位置即最优的输入层权值[ωi]和隐藏[bi]以及分类正确率,否则返回步骤2)。
4 计算机仿真结果与分析
实验环境为2.5 GHz CPU的Matlab 2015b。为了方便对比和讨论,设定PSO算法的迭代次数为20次[14](在不同输入数据维度和隐层神经元节点的情况下,粒子群算法在20次之前就能很好地收敛到一个稳定的状态,因此设定最大的迭代次数为20次),种群个体数为200,惯性权重[ω]为0.798,学习因子[c1],[c2]为1.496 1。本文算法中统一使用的距离度量为欧氏距离,激活函数为Sigmoid函数。
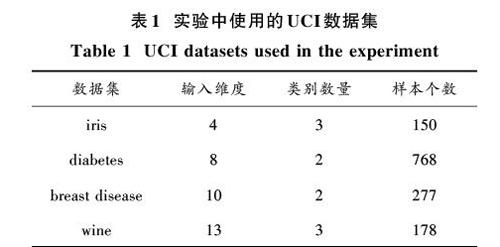
仿真所使用的数据来源于UCI机器学习数据库[9]的鸢尾花数据集(iris),糖尿病数据集(diabetes),乳腺癌数据集(breast disease),葡萄酒数据集(wine)。上述数据集被广泛应用于机器学习算法的测试。为了使算法更具有普遍性,使用十折交叉验证的方式进行计算,最后保留所有结果的平均值。数据的属性描述如表1所示。
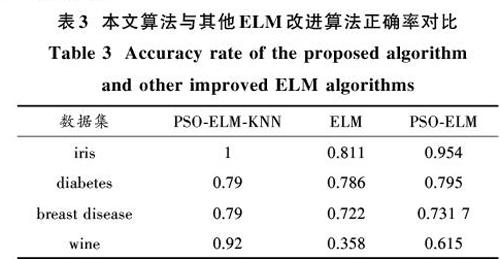
PSO?ELM?KNN算法、ELM算法以及PSO?ELM算法的分类正确率如表3所示。设定神经元个数为5个,[K]的个数为5。
以breast disease为例,计算PSO?ELM?KNN算法和ELM?KNN算法在不同神经元个数的情况下运行10次的分类正确率以及分类正确率方差变化情况,如图2,图3所示。

通過表2可以发现,PSO?ELM?KNN算法分类正确率明显高于KNN算法以及ELM?KNN算法。在选取不同[K]值时,KNN和ELM?KNN算法分类正确率会产生一定的影响,而本文算法在[K]大于5时,正确率基本保持不变,不会随着[K]的变化而对正确率产生影响。在表3的4个数据集中,PSO?ELM?KNN分类正确率明显高于ELM算法和PSO?ELM算法。通过图2,图3可以发现,随着特征空间维度的增加,ELM?KNN算法的分类正确率不断增加,达到400维度以上时其分类正确率趋于一个稳定的值。而PSO?ELM?KNN算法在特征空间维度很小时就能达到很高的分类正确率。
通过以上结果分析,可得到以下结论:
1) 本文算法的分类精确度高于其他算法。在多个数据集下实验得到的结果均显示PSO?ELM?KNN算法分类正确率高于KNN算法、ELM算法以及以上算法的组合。
2) 本文算法避免了[K]的确定过程。对于KNN算法以及ELM?KNN算法在不同数据集下,选取不同[K]值会产生不同的影响。针对[K]值选取往往需要多次实验,确定合适的[K]值。本文算法通过特征非线性映射,避免了[K]值变化产生的影响。实验结果发现,[K]值很小时即能达到很好的效果。
3) 本文算法需要映射的特征空间维度不需要太大,即需要的神经元个数较少。由于输入层权值和隐层偏差随机生成,ELM算法和ELM?KNN算法需要1 000个左右的神经元才能达到较高的稳定性和分类正确率。而PSO?ELM?KNN算法在维度为10时就能到达到很好的分类精确度以及稳定性,极大地降低了分类的时间复杂度。
5 结 语
本文提出PSO?ELM特征映射的KNN算法,并与ELM算法、KNN算法以及ELM?KNN算法的改进进行对比。该算法改善了ELM算法对样本进行特征非线性映射时的不足,以及[K]值和神经元个数选择的问题,提高了处理非线性问题分类正确率和算法的实用性。
参考文献
[1] 张昊,陶然,李志勇,等.基于KNN算法及禁忌搜索算法的特征选择方法在入侵检测中的应用研究[J].电子学报,2009,37(7):1628?1632.
ZHANG Hao, TAO Ran, LI Zhiyong, et al. A research and application of feature selection based on KNN and Tabu search algorithm in the intrusion detection [J]. Acta electronica Sinica, 2009, 37(7): 1628?1632.
[2] 周英,卓金武,卞月青.大数据挖掘[M].北京:机械工业出版社,2016.
ZHOU Ying, ZHUO Jinwu, BIAN Yueqing. Big data mining [M]. Beijing: China Machine Press, 2016.
[3] GUO G, WANG H, BELL D, et al. KNN model?based approach in classification [C]// 2003 International Conference on the Move to Meaningful Internet Systems. [S.l.]: Springer, 2003: 986?996.
[4] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications [J]. Neurocomputing, 2006, 70(1/3): 489?501.
[5] HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification [J]. IEEE transactions on systems, man & cybernetics, 2012, 42(2): 513?529.
[6] 李彬,李贻斌.基于ELM学习算法的混沌时间序列预测[J].天津大学学报,2011,44(8):701?704.
LI Bin, LI Yibin. Chaotic time series prediction based on ELM learning algorithm [J]. Journal of Tianjin University, 2011, 44(8): 701?704.
[7] MART?NEZ J M, ESCANDELL?MONTERO P, SORIA OLIVAS E, et al. Regularized extreme leaning machine for regression problems [J]. Neurocomputing, 2011, 74(17): 3716?3721.
[8] YU K, LIANG J, ZHANG X. Kernel nearest neighbor algorithm [J]. Neural processing letters, 2002, 15(2): 147?156.
[9] SHAWE?TAYLOR J, CRISTIANINI N. Kernel method for pattern analysis [M]. New York: Cambridge University Press, 2004.
[10] CAMASTRA F, VERRI A. A novel kernel method for cluste?ring [J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(5): 245?250.
[11] ALSHAMIRI A K, SURAMPUDI B R, SINGH A. A novel ELM K?Means algorithm for clustering [C]// 2014 International Conference on Swarm, Evolutionary, and Memetic Compu?ting. Switzerland: Springer, 2015: 212?222.
[12] 卢诚波,林银河,梅颖.基于ELM特征映射的KNN算法[J].复旦学报(自然科学版),2016,55(5):570?575.
LU Chengbo, LIN Yinhe, MEI Ying. KNN based on extreme learning machine feature mapping [J]. Journal of Fudan University (natural science), 2016, 55(5): 570?575.
[13] SARASWATHI S. ICGA?PSO?ELM approach for accurate multiclass cancer classification resulting in reduced gene sets in which genes encoding secreted proteins are highly represented [J]. IEEE/ACM transactions on computational biology and bioinformatics, 2011, 8(2): 452?463.
[14] UCI. UCI machine learning database [DB/OL]. [2012?04?23]. http://archive.ics.uci.edu/ml/datasets.html.
