基于耦合振子模型的含风电电力系统聚类同步
2019-03-12李静宇周明李庚银
李静宇 周明 李庚银
关键词: 图论; Kuramoto模型; Kron简化; 聚类同步; 耦合振子; 风电
中图分类号: TN99?34 文献标识码: A 文章编号: 1004?373X(2019)05?0135?06
Clustering synchronization of wind power system based on coupled oscillator model
LI Jingyu, ZHOU Ming, LI Gengyin
(State Key Laboratory of New Energy Power System, North China Electric Power University, Beijing 102206, China)
Abstract: A network coupled clustering synchronization method based on Kuramoto model is proposed to solve the serious system synchronization problem caused by the disturbance of the wind power electric system. The graph theory is used to establish the power network contraction model. On this basis, the electric system equivalent model based on Kuramoto coupled oscillator model is established, and a power network clustering algorithm based on dynamic coupling strength is proposed. This method can quickly and accurately cluster the synchronous state of oscillator in the system after system disturbance. The 39?node New England system with wind farms is verified. The simulation results show that the cluster analysis can understand the synchronization state of the power grid clearly, and avoid the further collapse of the system.
Keywords: graph theory; Kuramoto model; Kron reduction; clustering synchronization; coupled oscillator; wind power
0 引 言
随着电力系统的不断互联,电网的规模变得越来越复杂,而新能源发电技术的发展,也使得越来越多的间歇性电源接入到了电力系统中。由于以风电为代表的间歇性电源具有很强的随机性和波动性,且通过电力电子设备与电网相连,对电网缺少必要的惯性支撑。因此,对含风电的电力系统遭受严重暂态扰动后系统保持同步的能力提出了更高的要求[1]。目前常用的电力系统同步能力评价的方法大致可以分为:采用数值积分手段直接求解系统的状态方程,观察系统受扰后状态变量的变化轨迹的时域仿真法[2],根据动力学系统的稳定性理论来构造系统的暂态能量函数,并由暂态能量函数的性质判断受扰系统稳定性的直接法[3]。传统电力系统同步能力评价方法需要先确定系统受到扰动后的临界能量或不平衡点,当对大系统求解时方程维度高,求解难度大,多机系统适应性差。通过对系统进行等值虽然可以减小计算复杂度,但系统很多重要的节点信息也随着系统等值被忽略。近年来随着复杂网络同步理论以及图论理论的发展,在最大限度保留网络中节点和支路信息的情况下,计及系统中各节点之间的耦合关系对系统受到扰动后聚类同步过程的影响逐渐成为研究热点[4]。
1 基于图论的电力系统表征
在图论中通过定义一个无向图[G],包含一个[n]维节点集[V]和一个[e]维弧集[E]来表征網络所包含的信息。如果节点[vi]和节点[vj]由一条弧进行连接,即[e=(vi,vj)]。那么就称作节点[vi]是节点[vj]的一个邻居节点。如果图[G]中任意两对节点可以通过一条弧进行连接,那么该图形就是强连接的。因此,从网络拓扑的角度可以建立电力系统的电力网络保持模型或电力网络收缩模型。而对于任意一个电力网络都可用其邻接矩阵表示,邻接矩阵反映节点与弧之间的连接关系。在进行潮流计算时可用式(1)表示:
[Ax=y] (1)
式(1)与无向图存在如下映射关系。[V]中每一个节点[vi]与[x,y]中每一个元素[xi,yi]形成双映射。同时无向图[G=][(V,E)]存在映射[φ]:[E→R],使得[ωij=φ(eij)],则称[ωij]为弧[eij=(Vi,Vj)∈E]的权重,并用[G=(V,E,W)]表示加权图[5]。与图形相关的[N]维无向图[G]的邻接矩阵[A=aij∈Rn×n]表示为:
[aij=1, (vi,vj)∈E0, 其他] (2)
图的度矩阵是一个[n×n]的对角线矩阵[Δ=diag(degout(Vi))],对角线元素表示各节点的出度,而其他元素均为零。图[G]的定向可以为每条边赋予一个方向,所以边[(i,j)]是一条从节点[i]到节点[j]的弧线。定向为[σ]的图[G]可以表示为[Gσ]。定向图[Gσ]的关联矩阵[B(Gσ)]是一个[n×e]矩阵,该矩阵的行和列可以分别通过图[G]的节点及与之相连的弧进行表示。如果节点[j]通过弧进入节点[i],那么[B(Gσ)]的[(i,j)]就等于1;如果弧是从节点[i]进入到节点[j],则等于-1;其他情况则为0。
由于电网拓扑结构中的节点和边是不同质的元件,采用有权无向网络可以更好地表达电网中不同元件的獨特信息即[aij=aji=ωij],分析过程中通常采用导纳作为边权。因此,通过将网络的中节点分为边界节点和内部节点,采用Kron简化对内部节点进行消除,简化后的网络不仅保留了原来电力网中同步发电机终端电压和电流之间的关系,同时节点数量得到了大幅简化。网络中的电流平衡方程可以写为:
[I1I2=Q11Q12Q21Q22U1U2] (3)
式中:[I1]为外部节点的电流向量;[I2]为内部节点的电流向量;[U1]为外部节点的电压向量;[U2]为内部节点的电压向量;[Q11]为外部节点导纳矩阵;[Q22]为内部节点导纳矩阵;[Q12],[Q21]为内外节点互导纳矩阵。通过消去内部电压节点[U2]可以得出简化后的电流平衡方程为:
[I1-Q12Q-122I2=(Q11-Q12Q-122Q21)U1] (4)
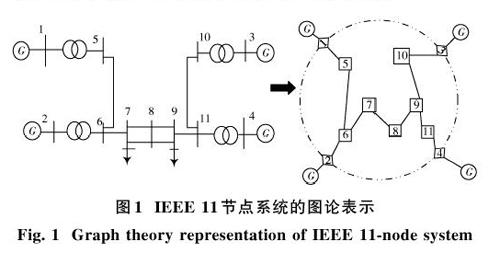
令矩阵[Q11-Q12Q-122Q21=Qred]为[Q]中内部节点的尔补码,因此[Qred]为相对于电力网络图[G]外部节点[U1]的Kron简化矩阵。利用图形理论基本原则,可以将电力系统建模成如图1所示的电力系统收缩网络。
因此将含风电的电力系统同步问题作为一个特殊的广义同步问题,通过Kuramoto模型进行分析,就可以通过Kron简化实现所有发电机之间的完全互连。
2 Kuramoto模型
2.1 耦合振子模型
一个包含[N]个耦合振子的网络,其动力学方程可以通过Kuramoto模型描述为:
[θi=ωi-j=1nKijsin(θi-θj)] (5)
式中:[θi]表示振子相位;[K]表示耦合强度;[ωi]表示振子固有频率。耦合强度是表征系统同步的重要参数,如果系统耦合强度弱,则系统中振子就会以与自身固有频率不同步的方式运行;反之,如果耦合强度超过相位差保持稳定的临界值,则会导致振子之间耦合,进而实现同步。对于包含[N]个振子的系统而言,可以通过定义全局序参量[r],对系统的同步进行解释。假定[N]个振子是一个圆上的各个点,且这些点会随不同角速度进行移动,那么在完全同步的情况下,所有点都会同步地围绕着这个圆进行移动,如图2所示。作为同步自然测度的各点中心的有序参数可以被定义为:
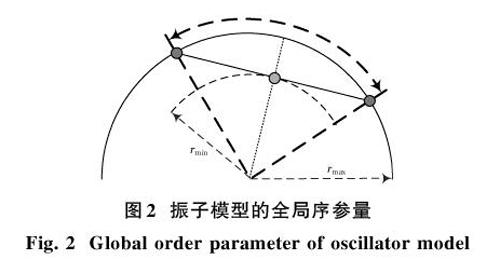
[r(t)e(i?(t))=1Nj=1ne(iθj(t))] (6)
式中:[r(t)∈](0,1),用于衡量这个网络中振子的相位同步程度;[?(t)]为平均相位。[r]值反映了系统内处于同步簇中的节点数量占整个系统中节点数量的比例,[r]越接近1,表明网络中的振子相位同步程度越高,[r=0]表示网络中的振子相位不同步[6]。将式(6)左右两边同时乘以[e-iθi]后代入到式(5)中,得到通过全局序参数表示的Kuramoto模型:
[θi=ωi-Krsin(?i-θi)] (7)
由式(7)可知:随着耦合强度[K]趋于零,各振子会根据其自由频率进行震荡,进而导致[r]趋于0;反之,当耦合强度[K]趋近于无穷大时,振子会逐渐与它们的平均相位同步,即[r]逐渐趋近于1。
2.2 基于Kuramoto模型电力系统等值模型
一个多机电力系统的详细动态模型包括有转子摆动、转子磁链、动态控制等耦合非线性模型。因此,通过建立完整上述模型来表示整个电力系统是非常困难的。对于具备非转移电导的多机电力系统而建立的Kuramoto模型,各发电机可以通过潮流进行耦合,将同步问题视为暂态稳定问题的一个特例。因此,可以从发电机动力学方程入手,建立基于Kuramoto模型的电力系统等值模型[7]。
一个由[n]台发电机组构成的电力系统中,第[i]台同步发电机的转子运动方程可表示为:
[Hiπfδi+KDiπfδi=PTi-PEi] (8)
式中:[Hi,δi,KDi,PTi,PEi]表示系统中第[i]台同步发电机的惯性时间常数、转子角度、阻尼系数、输入的机械功率以及输出的电磁功率的标幺值; [f]表示同步频率。
令[Mi=2Hiω0,Di=KDiω0],则式(8)变为:
[Miδi=PTi-PEi-Diδi] (9)
在电力网络收缩模型中,可以将系统中的同步发电机视为电压源,在发生短路故障后通过暂态电抗[x′di]与电网中相应的同步发电机节点相连。设[E′i]为受到扰动后的电势,同步发电机发生短路故障后的电势可写成如下形式:
[E′i=Vi+jx′diIi=Vi+jx′di(PGi-jQGiVi)] (10)
同时,在电力系统网络收缩模型中,为了分析发电机节点的动态特性,通常将负荷视为恒定阻抗。对于由[n]个发电机节点和[m]个负荷节点组成的系统,通过在每个发电机节点处增加一个发电机内节点,以此来形成增广网络,此时网路中节点总数[N=2n+m]。考虑到在增广网络中负荷不仅存在于负荷节点,还有可能在所有发电机的机端节点处[8]。因此,电力系统网络收缩模型中的负荷导纳为:
[yLi=(PLi-jQLi)Vi2] (11)
式中:[Pi,Qi]分别为节点[i]处的有功、无功负荷;[Vi]为稳态时节点[i]电压的模。
令[Y′di=diag(yd)]代表发电机暂态导纳矩阵;[Y′GL=diag(yGL)]代表发电机机端节点所带负荷等值之后的导纳矩阵;[Y′LL=diag(yLL)]代表负荷节点所形成的导纳矩阵。因此增廣网络导纳矩阵可表示为:
[Y=Y′d-Y′d0-Y′dYGG+Y′d+Y′GLYGL0YLGYLL+Y′LL] (12)
令[Y11=Y′d],[Y12=-Y′d0T],[Y21=-Y′d0T],[Y22=YGG+Y′d+Y′GLYGLYLGYLL+Y′LL]。
因此得到修改后网络的节点电压方程如下:
[In0=Y11(n×n)Y21(m×n) Y12(n×m)Y22(m×m)VnVm] (13)
使用Kron简化的方法消去输出电流为0的节点来对导纳矩阵进行化简,得到仅由[n]个外部发电机内节点构成网络,其内部则是全联通的。简化后的导纳阵为:
[Yred=Y1-Y12Y-122Y21] (14)
用[Yij,red]表示简化后导纳阵[Yred]中第[i]行、第[j]列的元素,则有:
[Yij,red=Gij,red+jBYij,red=Yij,red∠φij] (15)
式中[φij]表示简化后网络中的导纳阵[Yred]中第[i]行,第[j]列的元素所对应阻抗的相角。因此,简化后系统中任意一台同步发电机组输出的功率可表示为:
[PEi=E′i2Gii,red+E′ij∈I,j≠iE′jYii,redsinδij+φij] (16)
式中:[δij]为简化后系统中节点[i]与节点[j]间短路故障后电位的相角差;[E′i2Gii,red]为简化后网络中节点[i]处的负荷。
在这里假设简化后的网络是无损的,即[Gii,red=]0,[i≠j],则式(16)变为:
[PEi=E′i2Gii,red+E′ij∈I,j≠iE′jYij,redsinδi-δj] (17)
将式(17)代入同步发电机转子运动方程中,因此对于收缩网络有:
[Miδi+Diδi=PTi-E′i2Gii,red-E′i?j∈I,j≠iE′jYij,redsinδi-δj] (18)
令[Pi=PTi-E′j2Gii,red]表示简化后网络中节点[i]的注入功率,[Pmax=E′iE′jYii,red]表示简化后的网络中节点[i,j]间能够传输功率的最大值,因此可以将式(18)写为:
[Miδi+Diδi=Pi-j∈I,j≠iPmaxijsinδi-δj] (19)
以风电为代表的清洁能源在接入电网时,通过电力电子设备与电网进行功率交换,与传统同步机相比缺少对系统惯性的支撑[9],因此当考虑接入点为风电时的振子模型采用Kuramoto一阶模型表示:
[Diδi=Pi-j∈I,j≠iPmaxijsinδi-δj] (20)
式中[δ]为电力电子设备的相角。
3 电网的动态耦合强度聚类模型及算法
通过2.2节分析可知,在类Kuramoto电力网络模型中,各节点之间的耦合强度可由两节点间传输的最大功率来表示。当系统发生故障后,潮流分布发生转移,节点之间的耦合强度也随之改变,网络中各节点的稳定状态也发生改变,此时网络有可能存在多种同步状态。因此这里通过引入动态耦合强度分析各节点的不同同步状态,更快更合理地将电网中节点分群。
令式(7)中[K=αK′i],其中[K′i]是耦合强度,[α]是耦合权重,其表达式为:
[α=ηNj=1Ncos(θi-θj)] (21)
式中[η]称为可塑性参数,由式(21)可知,耦合权重[α]的大小取决于振子相对时序。文献[10]对耦合振子相互作用强度与振子之间的相互作用的相对时间的动态特性进行了深入研究,此处不再赘述。
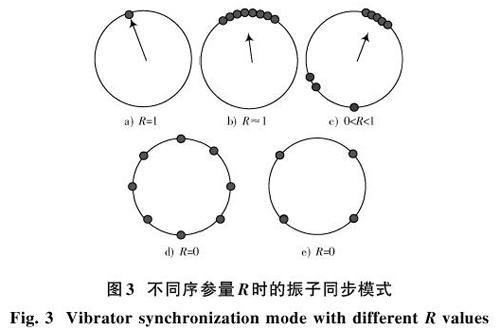
图3表示序参量与振子同步模式之间的关系,从图中可以看出,当系统发生扰动时如果没有足够大的耦合强度[K],则系统将出现从图3a)~3c)逐渐失去同步过程的情况。当[K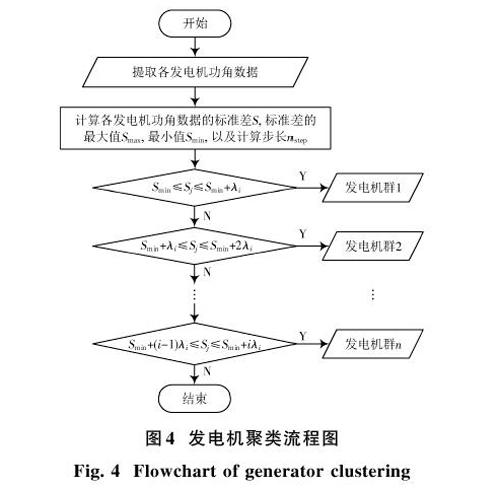
电网的动态耦合强度的聚类算法流程和步骤如图4所示。
1) 设置系统故障,记录故障前后各发电机转子角曲线。
2) 计算所有发电机转子角在时间序列上的标准差。
3) 计算不同聚类的数量下标准差和步长的最小值和最大值。
4) 根据步长,按转子角同步状态将发电机聚类。
4 算例分析
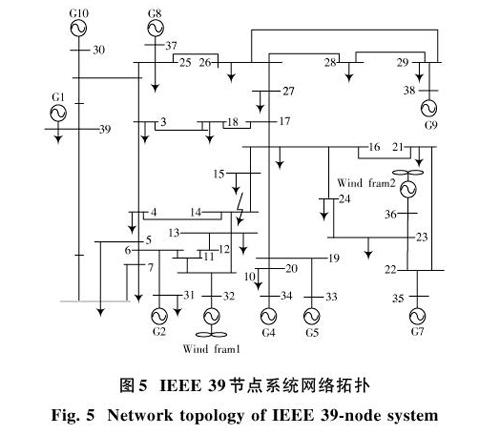
IEEE 39节点系统的网络拓扑结构如图5所示,该系统包含10个发电机节点、19个负荷节点以及46条输电线路,其中3号和6号发电机节点由相应容量的风电场替代。
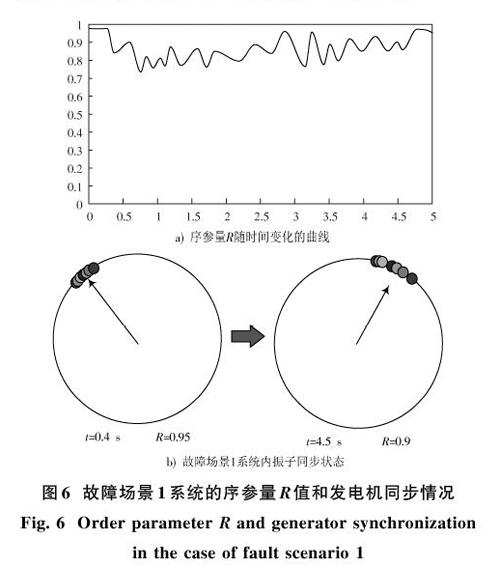
设置故障场景1参数为:仿真时间为5 s,在0.4 s时节点14发生三相短路故障,经过0.02 s故障清除。网络全局序参量[R]随时间变化的曲线如图6a)所示。
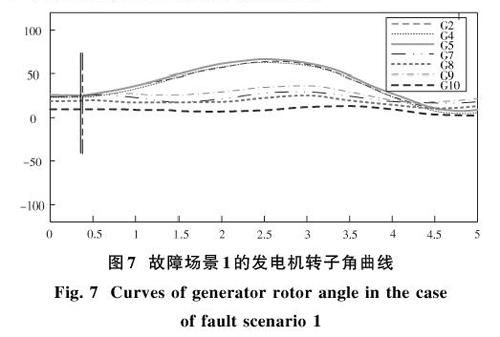
在整个故障发生前系统全局序参量[R]等于1,系统同步状态近似于图3a)。系统发生故障后,系统内振子同步状态发生了改变,由于故障持续时间短,因此没有出现图3c)中失去同步的情况,并最终恢复同步,此时序参量[R]接近于1,系统内振子同步状态如图6b)所示。图7为系统内各发电机转子角随时间变化曲线,从图中可知故障清除后系统内4,5,7号发电机组转子角发生了小幅震荡,但最终恢复到初始值。
设置故障场景2参数为:仿真时间为5 s,在0.4 s时节点14发生三相短路故障,风电场从系统中切除,0.6 s后故障清除。故障清除后将系统发电机按照同步状态聚类成三个机群。其中编号为2,4,5的发电机组为机群1,编号为8,9,10的发电机组为机群2。7号发电机为机群3。网络中振子聚类后的各机群的序参量[R1,R2,R3]随时间变化的曲线如图8a)所示。聚类后各机群本身是同步的,因此[R1,R2]的数值接近于1,由于机群3中只有7号发电机一台机组,因此[R3]的值等于1。系统内振子同步状态如图8b)所示。

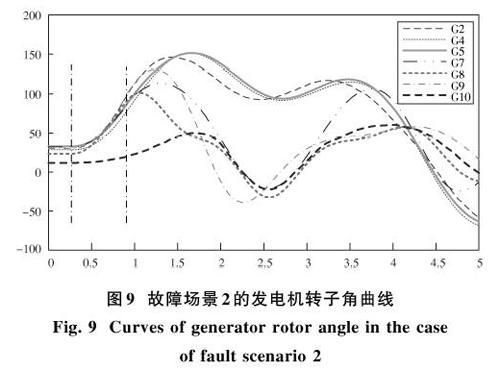
圖9为系统内各发电机转子角随时间变化曲线,从图中可知故障清除后,系统内振子失去同步,其中2,4,5号发电机组转子角波动趋势相近,8,9,10号发电机转子角波动趋势相近,7号发电机由于距离故障节点电气距离较近,其转子角波动变化较大,进而验证了聚类算法的正确性。
5 结 论
本文针对含有风电电力系统的同步问题提出基于Kuramoto模型的网络自适应耦合聚类同步方法,通过对聚类后各机群序参数的分析可以更清晰地了解网络的同步状态,避免完全崩溃。
参考文献
[1] 姜惠兰,吴玉璋,周照清,等.含双馈风力发电场的多机系统暂态功角稳定性分析方法[J].中国电机工程学报,2018,38(4):999?1005.
JIANG Huilan, WU Yuzhang, ZHOU Zhaoqing, et al. A method to analyze the transient angle stability of multi?machine system with DFIG?based wind farm [J]. Proceedings of the CSEE, 2018, 38(4): 999?1005.
[2] 苏福,杨松浩,王怀远,等.电力系统暂态稳定时域仿真快速终止算法研究[J].中国电机工程学报,2017,37(15):4372?4378.
SU Fu, YANG Songhao, WANG Huaiyuan, et al. Study on fast termination algorithm of time?domain simulation for power system transient stability [J]. Proceedings of the CSEE, 2017, 37(15): 4372?4378.
[3] 陈厚合,王长江,姜涛,等.基于投影能量函数和Pin?SVM的电力系统暂态稳定评估[J].电工技术学报,2017,32(11):67?76.
CHEN Houhe, WANG Changjing, JIANG Tao, et al. Transient stability assessment in bulk power grid using projection energy function and support vector machine with pinball loss [J]. Transactions of China electrotechnical society, 2017, 32(11): 67?76.
[4] 王丽娟,蔡晓东,杨超,等.基于优化结构洞的无向加权网络关键节点发现方法[J].现代电子技术,2017,40(6):35?39.
WANG Lijuan, CAI Xiaodong, YANG Chao, et al. Method to identify key nodes in undirected weighted networks on basis of optimized ″structural hole″ [J]. Modern electronics technique, 2017, 40(6): 35?39.
[5] DORFLER F, SIMPSON?PORCO J W, BULLO F, et al. Networks and algebraic graph theory: models, properties, and applications [J]. Proceedings of the IEEE, 2018, 106(5): 977?1005.
[6] 陆君安,刘慧,陈娟.复杂动态网络的同步[M].北京:高等教育出版社,2016:50?79.
LU Junan, LIU Hui, CHEN Juan. Synchronization in complex dynamical networks [M]. Beijing: Higher Education Press, 2016: 50?79.
[7] LI B, WONG K Y M. Optimizing synchronization stability of the Kuramoto model in complex networks and power grids [J]. Physical review E, 2017, 95(1): 1?7.
[8] 吴成业,刘光晔,孙瑞,等.应用潮流方程简化网络计算的电力系统小干扰稳定分析[J].电力系统及其自动化学报,2018(6):10?15.
WU Chengye, LIU Guangye, SUN Rui, et al. Small signal stability analysis of power system with simplified network compu?ting using power flow equations [J]. Proceedings of the CSU?EPSA, 2018(6): 10?15.
[9] 黄李,邹艳丽,王意,等.分布式电站的3种入网方式比较研究[J].广西师范大学学报(自然科学版),2017,35(3):30?36.
HUANG Li, ZOU Yanli, WANG Yi, et al. A comparative study on three types of distributed power plant connection stra?tegies [J]. Journal of Guangxi Normal University (natural science edition), 2017, 35(3): 30?36.
[10] CHANDRASEKAR V, SHEEBA J H, SUBASH B, et al. Adaptive coupling induced multi?stable states in complex networks [J]. Physica D: nonlinear phenomena, 2014, 267: 36?48.
