ECG信号自适应贝叶斯小波去噪算法研究

赵静 韦海成

关键词： 贝叶斯; 小波分析; 心电图; 信号去噪; 信号重构; 小波阈值

中图分类号： TN911.4?34                       文献标识码： A                          文章編号： 1004?373X（2019）05?0061?05

Research on ECG signal′s adaptive denoising algorithm based on

Bayesian wavelet analysis

ZHAO Jing1， WEI Haicheng2

（1. School of Information Engineering， Ningxia University， Yinchuan 750021， China;

2. School of Electrical and Information Engineering， North Minzu University， Yinchuan 750021， China）

Abstract： ECG signal is one of bioelectric signals in current mobile health monitoring. The noise may be introduced in conventional hardware amplification circuit in the process of ECG signal collection， which can affect the characteristic analysis of the signal. A denoising algorithm based on Bayesian wavelet analysis is proposed to denoise the noise in ECG signal acquisition. The wavelet decomposition is performed for ECG signal， and then the Bayesian algorithm is used to recalculate the best wavelet coefficient threshold and weighted coefficient to realize the denoising and reconstruction of ECG signal. The experimental results show this algorithm can eliminate the noise of ECG signal effectively， retain more signal details， and reduce the signal distortion. The mean square error （MSE） and peak signal?to?noise ratio （PSNR） of the algorithm are 0.287 1 and 53.550 7 respectively， which are superior to the wavelet soft threshold and hard threshold algorithms， and the algorithm has high practical use value.

Keywords： Bayesian algorithm; wavelet analysis; ECG; signal denoising; signal reconstruction; wavelet threshold

0  引  言

随着当前移动健康监护技术的发展，利用小型便携装置对人体实时采集心电图（ECG）等生物电信号进行分析是当前研究的一个热点领域。然而在实际使用过程中，由于ECG信号幅度为mV级，这种级别的电信号通常会遇到电路背景噪声、50 Hz工频等环境噪声的影响，出现信号干扰和失真，影响了对该信号的正确分析[1]。

为了消除噪声对信号的干扰，ECG信号放大电路中常采用前段放大、高通滤波、带通滤波和放大电路等多级环节构成ECG电信号放大系统，并在临床中取得了较好的效果[2]。但在实际使用中发现，ECG信号经过上述硬件处理后仍存在一定的高频噪声和零点漂移现象。上述噪声虽然对有经验的医师判断疾病没有较大的影响，但在采用机器视觉进行移动健康动态监控时会影响到ECG周期性特征点的分析。因此，需要采用算法对采集到的ECG信号进行噪声消除。

当前消除ECG噪声的算法比较多，除了形态分析滤波[3]，还有小波变换[4]、Hilbert?Huang变换[5]和自适应去噪[6]等方法。其中，小波变换以其良好的局域化时频特性在ECG信号处理方面得到了广泛应用。

为了减少采集信号中的噪声、提高信号可识别性，本文在自建ECG信号采集硬件系统的基础上，研究贝叶斯阈值算法的小波分解在ECG波形去噪方面的应用，优化小波去噪的阈值系数，以实现ECG信号的去噪。

1  ECG信号及其信号采集系统

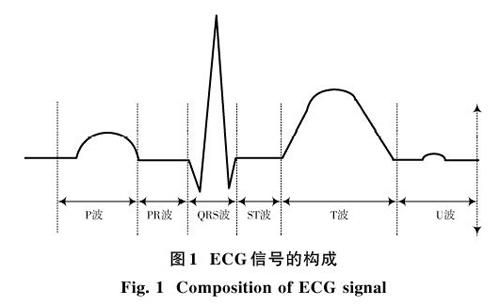
ECG信号属于人体生物电信号，该信号反映了心肌细胞在电激动时产生的电传变化。正常的跨膜动作电位按周期变化，每个周期可以分成多个时相，分析该信号可以对心律失常、心肌梗死、心衰等病症进行辅助诊断。从波形上看，ECG信号共由6段信号构成，其中P波段反映了心房去极化过程，幅度仅为0.25 mV;QRS波段反映了左右心室肌细胞去极化过程产生的膜外负电压，幅度约为4 mV，持续时间约0.1 s;T波段反映了心室肌细胞复极化过程，幅度为0.1～0.8 mV，整个波形如图1所示。

ECG信号在一个周期中大部分时间里幅度都比较小，极易受基线漂移、工频干扰、电极接触噪声及运动伪迹等波形干扰和噪声的影响[7]。为消除硬件噪声，本文实验搭建的ECG平台主要由传感器、仪表放大器、工频滤波器、带通滤波器、后级放大器、电位调整电路、数据采集卡和LabVIEW上位机软件构成，如图2所示。

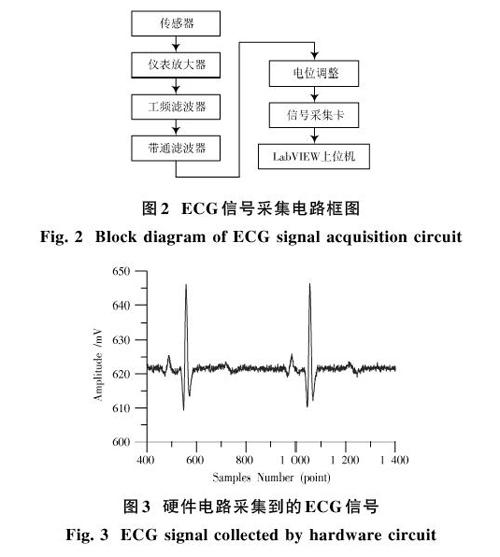
平台工作时，用传感器对ECG信号进行采集后，通过仪表放大器电路进行放大并去除共模信号，然后由工频滤波器消除50 Hz电源干扰，再通过带通滤波和电位调整将信号钳位到合适的范围，最后由USB6909数据采集卡进行数模转换，通过PC的USB端口将数字信号送至LabVIEW上位机软件进行显示处理，上位机得到的ECG信号如图3所示。利用上述硬件电路采集的ECG信号相对比较稳定，QRS段、T段、P段等有剧烈变化的信号得到了较为准确的显示，然而在信号变化较小的波段区间内，信号噪声却没有消除干净，影响了最终的显示效果。

ECG信号中混杂的噪声有乘性噪声[ηm（x，y）]和加性噪声[ηa（x，y）]。通过上述信号放大降噪采集电路可以较好地消除加性噪声[ηa（x，y）]，但很难消除乘性噪声[ηm（x，y）]。因此，图3中ECG信号已经没有明显的零点漂移、共模、共频等噪声的影响，但在PR波段和ST波段的高频底噪仍无法较好地消除，这将影响到通过机器视觉算法进行的ECG特征分析和识别。

2  采用小波分析对ECG信号进行处理

考虑到ECG信号中有用信息与噪声的区分，如果算法不能区分信息和噪声，就会导致在滤除噪声的同时将有用信息的局部细节丢失或者噪声滤除过少，起不到消除噪聲的目的。以最小均方自适应算法为例，由于计算波形均方差后很难定位叠加初始时间基准节点，因此该算法能够很好地消除P段和T段小幅度噪声，但对大幅度的信号QRS段滤除并不理想。而小波变换算法能够利用多种分辨率解析信号，在表征局部信号特征方面有独特的优势，因此更适应于这种有局部突变的信号处理。

采用小波变换分析ECG信号时，变换中采用变换时间窗口应对短暂的高频信号变化，分析出信号变化趋势;采用多分辨率结构，对信号非平稳阶段不同频率信号的系数进行处理以消除噪声，保持原始信号的完整性，降低信号的失真。

常见的小波变换消除噪声有模极大值去噪[8]、相邻尺度系数相关性去噪[9]和阈值去噪[10]等算法。其中，模极大值及相邻尺度系数相关性算法较为复杂，很难满足移动ECG监测过程中的实时要求;阈值去噪的算法简单，实现方便，在移动监测领域有着较为广泛的应用。

小波阈值去噪的主要思想是将ECG信号经过小波分解后，分析信号的小波系数和阈值[T]的关系。如果含噪声ECG信号[I（x，y）]对应的小波系数为[Wi（j，k）]。当[Wi（j，k）]大于阈值[T]，则认为此时波形主要为有用信息;当[Wi（j，k）]小于阈值[T]，则认为此时信息为噪声。将ECG信号分解为不同层次的小波，选择合适的阈值处理各层信号的系数，再重构信号就能够消除噪声。在此过程中，小波分解的阈值选择会影响信号去噪的准确性。

常用的小波阈值处理主要有硬阈值和软阈值两种方法。ECG信号的噪声符合高斯白噪声特征，如果对该信号采用硬阈值去噪，处理结果对阈值周围的微小变化很敏感，会导致信号局部抖动;采用软阈值函数则会导致剧烈信号变动的区域存在较大的差值，使得重构信号在大幅变动区域产生较大失真。为了防止信号在去噪的过程中出现失真，需要采用对阈值估算的方法进行改进。在对阈值估算进行改进的算法中，贝叶斯估值算法可以最大程度地确保信号不失真。

贝叶斯估值算法可以在局部区域内对小波系数进行分析，并通过概率学统计方法对噪声进行自适应阈值选择，最大程度保存信号的完整性，是一种较好的一维小波信息去噪方法。其选取阈值的方法主要是通过对检测到的数据进行系统分析后，利用先验概率和代价因子构成似然比检测门限，然后进行整个信号的阈值估算。阈值估算过程为：

1） 对ECG信号进行小波变换，得到小波分解各个子带系数;

2） 对系数的密度函数建模，计算出小波系数估计量;

3） 根据估计出来的小波新系数重构信息，得到去噪后的ECG信号。

根据贝叶斯法则，贝叶斯最优估值系数满足无偏最小方差，当噪声服从[σ2x]高斯分布时，信号的小波系数也应当服从广义高斯分布。对其高频小波系数进行分析可知，高频子带最优阈值[T]可以写为：

[T=σ2σx] （1）

式中[σ]为噪声的方差估计值，其值大小为：

[σ=median（Yx）0.674 5] （2）

[σx]为解析后的小波系数方差，由于信号小波系数与噪声小波系数相互独立，有：

[σx=max（σ2Y（x）-σ2（x），0）] （3）

式中[σ2Y（x）]为含噪ECG信号的方差。

通过计算[T]就能够得到阈值最佳点。在此基础上，对现有软硬件阈值算法进行改造，得到最终阈值：

[δ（x）=sgn（x）max（x-aT），0，   a∈（0，1）] （4）

利用最终阈值进行小波系数的选择就能够较好地消除ECG信号的噪声。

3  基于贝叶斯小波分析的ECG去噪实验

算法流程如下：

1） 对原始信号进行多级小波变换;

2） 在小波子带中采用上述贝叶斯阈值方法进行去噪，去噪阈值由计算噪声方差和信号方差来确定阈值;

3） 将调整的系数进行加权平均，完成小波逆变换，实现信号的复原。

实验选取ECG波形为图3中采集到的含噪波形，波形共3 000点，经过小波分解后形成如图4所示的三级子带。

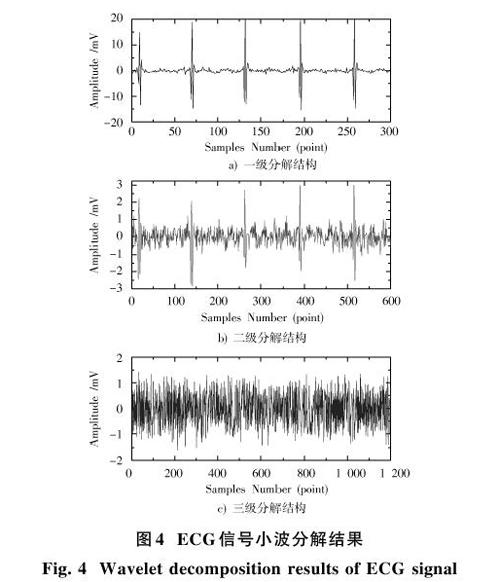
图4表明，该含噪ECG信号在小波分解后，不同子带对信号的细节贡献是不一样的，保留的子带权系数越大，该子带的细节信息在逆变换后就能够得到更多的保持;权系数越小，该子带的噪声就越容易得到消除。

4  实验结果及分析

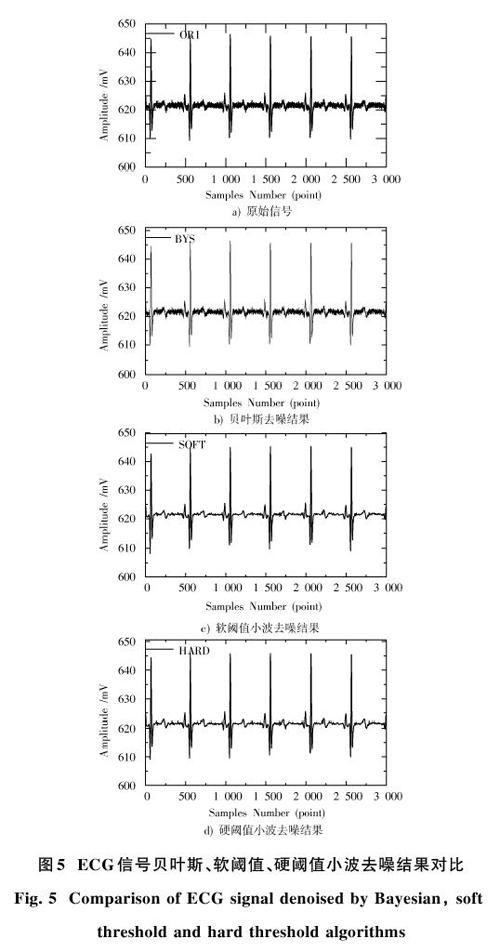
为了进一步分析贝叶斯小波去噪与其他阈值去噪的区别，将图3的信号采用贝叶斯阈值、软阈值、硬阈值三种算法进行处理，处理后的图像如图5所示。从对比图来看，三种算法都能够较好地消除ECG噪声，但从细节上来看，贝叶斯算法去噪后信号细节更为丰富，更接近原始信号。在图6的局域放大图像中可以看到，贝叶斯算法在575～600点这一段变化平滑，没有软阈值和硬阈值图像出现的抖动，与真实图像更为一致;在650点附近更为清晰地反映了原始图像的一个抖动，该抖动在其他两个算法中被忽略掉了。

为了进一步客观评价该信号的区别，实验采用最小均方误差MSE和信噪比PSNR两个指标对三种去噪方式进行评价。最小均方误差用式（5）计算，信噪比采用式（6）计算：

[MSE=1n2i=1n（xi-xi）2]  （5）

[PSNR=10lgσ2MSE] （6）

式中：[xi]表示去噪后信号;[xi]表示原始信号;[σ2]表示重建后ECG信号的方差。经过计算后，上述三种方法的MSE和PSNR值如表1所示。

由表1可以看出，采用本文所述的貝叶斯算法重建后信号的PSNR值为53.550 7，高于其他两种方法。MSE为0.287 1，低于其他两种方法，表明本文提出的算法优于软阈值和硬阈值算法。

5  结  论

本文提出的贝叶斯阈值去噪算法的实验结果表明：在小波阈值去噪算法中，硬阈值、软阈值及贝叶斯算法均可以消除ECG信号上的噪声。但从重建信号波形细节上来看，贝叶斯算法能够较好地保留信号细节，消除高频噪声，使得信号得到了较好的复原，可提高信号的辨识性，具有较好的实际应用价值。

参考文献

[1] 王吉鸣，吕颖莹，董晗，等.一种滤除高采样心电工频干扰的改进算法[J].中国生物医学工程学报，2016，35（6）：744?748.

WANG J M， L? Y Y， DONG H， et al. An improved algorithm for removing the power?line interference from ECG signals in high sampling rate [J]. Chinese journal of biomedical engineering， 2016， 35（6）： 744?748.

[2] 何伶俐，王宇峰，何汶静，等.ECG监护仪检测放大电路的设计[J].生物医学工程研究，2013，32（1）：31?34.

HE Lingli， WANG Yufeng， HE Wenjing， et al. Design of detection amplifier circuit for electrocardiogram monitor [J]. Journal of biomedical engineering research， 2013， 32（1）： 31?34.

[3] 赵伟，陈仁安，黄晓菁，等.基于形态分量分析的心电信号去噪[J].实验室研究与探索，2015，34（4）：61?63.

ZHAO W， CHEN R A， HUANG X J， et al. Study on ECG signal denoising based on morphological component analysis [J]. Research and exploration in laboratory， 2015， 34（4）： 61?63.

[4] 彭自然，王国军.用小波变换对ECG信号进行去噪研究[J].信 号处理，2017（8）：1122?1131.

PENG Z R， WANG G J. Denoising of ECG signal by wavelet transform [J]. Journal of signal processing， 2017（8）： 1122?1131.

[5] 杨向林，严洪，许志，等.基于Hilbert?Huang变换的ECG消噪[J].电子学报，2011，39（4）：819?824.

YANG X L， YAN H， XU Z， et al. ECG de?noising based on Hilbert?Huang transform [J]. Acta electronica Sinica， 2011， 39（4）： 819?824.

[6] 程呈.自适应RLS算法在心电信号去噪中的研究[D].长沙：湖南大學，2015.

CHENG C. The research of adaptive RLS algorithm in ECG signal denoising [D]. Changsha： Hunan University， 2015.

[7] 戴明，陈昕，林浩明，等.一种基于织物电极的可穿戴心电采集系统的设计[J].生物医学工程研究，2017，36（3）：239?242.

DAI M， CHEN X， LIN H M， et al. Design of wearable electrocardiograph acquisition system with textile electrodes [J]. Journal of biomedical engineering research， 2017， 36（3）： 239?242.

[8] 赵鸿图，刘云.Blackman窗插值的小波模极大值去噪算法[J].计算机工程与应用，2015，51（13）：216?220.

ZHAO H T， LIU Y. Wavelet modulus maxima denoising algorithm based on Blackman window interpolation [J]. Computer engineering and applications， 2015， 51（13）： 216?220.

[9] 王晓燕，鲁华祥，金敏，等.基于相关性的小波熵心电信号去噪算法[J].智能系统学报，2016，11（6）：827?834.

WANG X Y， LU H X， JIN M， et al. Wavelet entropy denoi?sing algorithm of electrocardiogram signals based on correlation [J]. CAAI transactions on intelligent systems， 2016， 11（6）： 827?834.

[10] 郑敏敏，高小榕，谢海鹤.心电信号小波去噪的改进算法研究[J].中国生物医学工程学报，2017，36（1）：114?118.

ZHENG M M， GAO X R， XIE H H. Research on an improved algorithm for wavelet denoising of ECG [J]. Chinese journal of biomedical engineering， 2017， 36（1）： 114?118.