A Modified Gravity Theory: Null Aether∗
2019-03-12Metinrsesandetinentrk
Metin Gürses† and C¸etin S¸entürk‡
1Department of Mathematics, Faculty of Sciences, Bilkent University, Ankara 06800, Turkey
2Department of Physics, Faculty of Sciences, Bilkent University, Ankara 06800, Turkey
3Department of Aeronautical Engineering, University of Turkish Aeronautical Association, Ankara 06790, Turkey
(Received July 30, 2018; revised manuscript received October 2, 2018)
Abstract General quantum gravity arguments predict that Lorentz symmetry might not hold exactly in nature.This has motivated much interest in Lorentz breaking gravity theories recently.Among such models are vector-tensor theories with preferred direction established at every point of spacetime by a fixed-norm vector field.The dynamical vector field defined in this way is referred to as the “aether”.In this paper, we put forward the idea of a null aether field and introduce,for the first time,the Null Aether Theory(NAT)—a vector-tensor theory.We first study the Newtonian limit of this theory and then construct exact spherically symmetric black hole solutions in the theory in four dimensions,which contain Vaidya-type non-static solutions and static Schwarzschild-(A)dS type solutions, Reissner-Nordström-(A)dS type solutions and solutions of conformal gravity as special cases.Afterwards, we study the cosmological solutions in NAT:We find some exact solutions with perfect fluid distribution for spatially flat FLRW metric and null aether propagating along the x direction.We observe that there are solutions in which the universe has big-bang singularity and null field diminishes asymptotically.We also study exact gravitational wave solutions — AdS-plane waves and pp-waves — in this theory in any dimension D ≥3.Assuming the Kerr-Schild-Kundt class of metrics for such solutions, we show that the full field equations of the theory are reduced to two, in general coupled, differential equations when the background metric assumes the maximally symmetric form.The main conclusion of these computations is that the spin-0 aether field acquires a “mass” determined by the cosmological constant of the background spacetime and the Lagrange multiplier given in the theory.
Key words: Aether theory, Newtonian limit, black holes, cosmological solutions, Kerr-Schild-Kundt class of metrics, Ads-plane waves, pp-waves
1 Introduction
Lorentz violating theories of gravity have attracted much attention recently.This is mainly due to the fact that some quantum gravity theories, such as string theory and loop quantum gravity, predict that the spacetime structure at very high energies — typically at the Planck scale — may not be smooth and continuous, as assumed by relativity.This means that the rules of relativity do not apply and Lorentz symmetry must break down at or below the Planck distance (see e.g., Ref.[1]).
The simplest way to study Lorentz violation in the context of gravity is to assume that there is a vector field with fixed norm coupling to gravity at each point of spacetime.In other words, the spacetime is locally endowed with a metric tensor and a dynamical vector field with constant norm.The vector field defined in this way is referred to as the“aether”because it establishes a preferred direction at each point in spacetime and thereby explicitly breaks local Lorentz symmetry.The existence of such a vector field would affect the propagation of particles — such as electrons and photons — through spacetime, which manifests itself at very high energies and can be observed by studying the spectrum of high energy cosmic rays.For example, the interactions of these particles with the field would restrict the electron’s maximum speed or cause polarized photons to rotate as they travel through space over long distances.Any observational evidence in these directions would be a direct indication of Lorentz violation,and therefore new physics, at or beyond the Planck scale.
So vector-tensor theories of gravity are of physical importance today because they may shed some light on the internal structure of quantum gravity theories.One such theory is Einstein-Aether theory[2−3]in which the aether field is assumed to be timelike and therefore breaks the boost sector of the Lorentz symmetry.This theory has been investigated over the years from various respects.[4−22]There also appeared some related works,[23−26]which discuss the possibility of a spacelike aether field breaking the rotational invariance of space.The internal structure and dynamics of such theories are still under examination;for example,the stability problem of the aether field has been considered in Refs.[27–28].§Of course, to gain more understanding in these respects,one also needs explicit analytic solutions to the fairly complicated equations of motion that these theories possess.
In this paper, we propose yet another possibility,namely,the possibility of a null aether field,which dynamically couples to the metric tensor of spacetime.From now on, we shall refer to the theory constructed in this way as Null Aether Theory (NAT).This construction enables us to naturally introduce a scalar degree of freedom, i.e.the spin-0 part of the aether field, which is a scalar field that has a mass in general.By using this freedom, we show that it is possible to construct exact black hole solutions and nonlinear wave solutions in the theory.¶In the context of Einstein-Aether theory, black hole solutions were considered in Refs.[4–13] and plane wave solutions were studied in Refs.[30–32].Indeed, assuming the null aether vector field (vµ)is parallel to the one null leg (lµ)of the viel-bein at each spacetime point,i.e.vµ=ϕ(x)lµ, whereϕ(x)is the spin-0 aether field, we first discuss the Newtonian limit of NAT and then proceed to construct exact spherically symmetric black hole solutions to the full nonlinear theory in four dimensions.In the Newtonian limit, we considered three different forms of the aether field: (a)vµ=aµ+kµwhereaµis a constant vector representing the background aether field andkµis the perturbed aether field.(b)ϕ=ϕ0+ϕ1andlµ=δ0µ+(1−Φ−Ψ)(xi/r)δiµwhereϕ0is a nonzero constant andϕ1is the perturbed scalar aether field.(c)The case whereϕ0=0.
Among the black hole solutions,there are Vaidya-type nonstationary solutions, which do not need the existence of any extra matter field: the null aether field present in the very foundation of the theory behaves, in a sense,as a null matter to produce such solutions.For special values of the parameters of the theory, there are also stationary Schwarzschild-(A)dS type solutions that exist even when there is no explicit cosmological constant in the theory, Reissner-Nordström-(A)dS type solutions with some“charge”sourced by the aether,and solutions of conformal gravity that contain a term growing linearly with radial distance and so associated with the flatness of the galaxy rotation curves.Our exact solutions perfectly match the solutions in the Newtonian limit when the aether field is on the order of the Newtonian potential.
We investigated the cosmological solutions of NAT.Taking the matter distribution as the perfect fluid energy momentum tensor, with cosmological constant, the metric as the spatially flat (k= 0)Friedmann-Lemaˆıtre-Robertson-Walker (FLRW)metric and the null aether propagating along thex-axis, we find some exact solutions where the equation of state is of polytropic type.If the parameters of the theory satisfy some special inequalities, then acceleration of the expansion of the universe is possible.This is also supported by some special exact solutions of the field equations.There are two different types of solutions: power law and exponential.In the case of the power law type, there are four different solutions in all of which the pressure and the matter density blow up att=0.In the other exponential type solutions case,the metric is of the de Sitter type and there are three different solutions.In all these cases the pressure and the matter density are constants.
On the other hand, the same construction,vµ=ϕ(x)lµ, also permits us to obtain exact solutions describing gravitational waves in NAT.In searching for such solutions,the Kerr-Schild-Kundt(KSK)class of metrics[33−38]was shown to be a valuable tool to start with: Indeed,recently, it has been proved that these metrics are universal in the sense that they constitute solutions to the field equations of any theory constructed by the contractions of the curvature tensor and its covariant derivatives at any order.[38]In starting this work, one of our motivations was to examine whether such universal metrics are solutions to vector-tensor theories of gravity as well.Later on, we perceived that this is only possible when the vector field in the theory is null and aligned with the propagation direction of the waves.Taking the metric in the KSK class with maximally symmetric backgrounds and assuming furtherlµ∂µϕ= 0, we show that the AdSplane waves andpp-waves form a special class of exact solutions to NAT.The whole set of field equations of the theory are reduced to two coupled differential equations,in general, one for a scalar function related to the profile function of the wave and one for the “massive” spin-0 aether fieldϕ(x).When the background spacetime is AdS,it is possible to solve these coupled differential equations exactly in three dimensions and explicitly construct plane waves propagating in the AdS spacetime.Such constructions are possible also in dimensions higher than three but with the simplifying assumption that the profile function describing the AdS-plane wave does not depend on the transverseD-3 coordinates.The main conclusion of these computations is that the mass corresponding to the spin-0 aether field acquires an upper bound (the Breitenlohner-Freedman bound[39])determined by the value of the cosmological constant of the background spacetime.In the case ofpp-waves, where the background is flat, the scalar field equations decouple and form one Laplace equation for a scalar function related to the profile function of the wave and one massive Klein-Gordon equation for the spin-0 aether field in (D-2)-dimensional Euclidean flat space.Because of this decoupling, plane wave solutions, which are the subset ofpp-waves, can always be constructed in NAT.
The paper is structured as follows.In Sec.2,we introduce NAT and present the field equations.In Sec.3, we study the Newtonian limit of the theory to see the effect of the null vector field on the solar system observations.In Sec.4, we construct exact spherically symmetric black hole solutions in their full generality in four dimensions.In Sec.5, we study the FLRW cosmology with spatially flat metric and null aether propagating along thexdirection.We find mainly two different exact solutions in the power and exponential forms.We also investigate the possible choices of the parameters of the theory where the expansion of the universe is accelerating.In Sec.6,we study the nonlinear wave solutions of NAT propagating in nonflat backgrounds, which are assumed to be maximally symmetric, by taking the metric in the KSK class.In Sec.7,we specifically consider AdS-plane waves describing plane waves moving in the AdS spacetime inD ≥3 dimensions.In Sec.8, we briefly describe thepp-wave spacetimes and show that they provide exact solutions to NAT.We also discuss the availability of the subclass plane waves under certain conditions.Finally, in Sec.9, we summarize our results.
We shall use the metric signature (−,+,+,+,...)throughout the paper.
2 Null Aether Theory
The theory we shall consider is defined inDdimensions and described by, in the absence of matter fields,the action
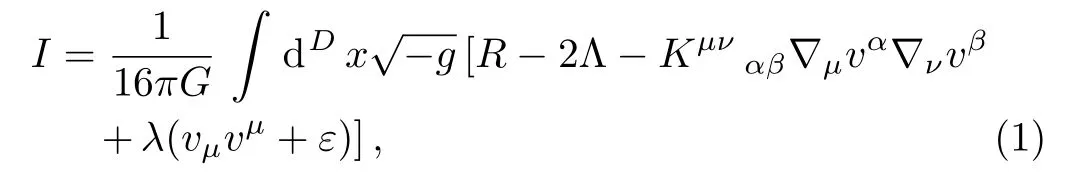
where

Here Λ is the cosmological constant andvµis the so-called aether field, which dynamically couples to the metric tensorgµνand has the fixed-norm constraint

which is introduced into the theory by the Lagrange multiplierλin Eq.(1).Accordingly, the aether field is a timelike (spacelike)vector field whenε=+1 (ε=−1),and it is a null vector field whenε= 0.||The case with ε=+1 is associated with Einstein-Aether theory.[2−3]The constant coefficientsc1,c2,c3andc4appearing in Eq.(2)are the dimensionless parameters of the theory.∗∗In Einstein-Aether theory, these parameters are constrained by some theoretical and observational arguments.[2−3,16,32,40−46]
The equations of motion can be obtained by varying the action (1)with respect to the independent variables:Variation with respect toλproduces the constraint equation(3)and variation with respect togµνandvµproduces the respective, dynamical field equations
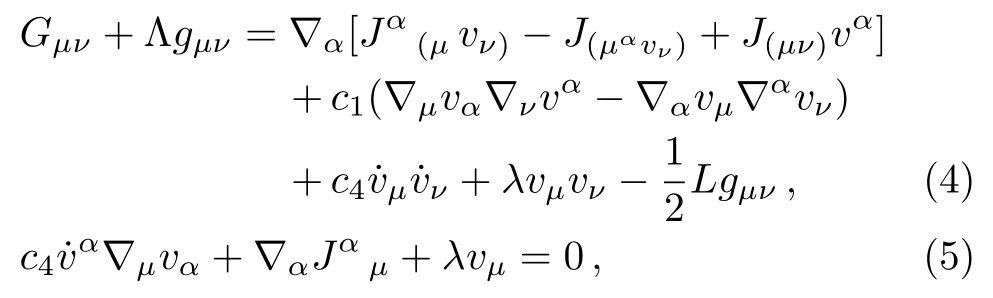
where ˙vµ ≡vα∇αvµand
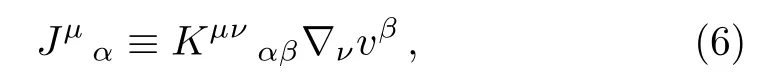

In writing Eq.(4),we made use of the constraint(3).From now on,we will assume that the aether fieldvµis null(i.e.,ε=0)and refer to the above theory as Null Aether Theory, which we have dubbed NAT.This fact enables us to obtain⟨from the aether equation(5)by contracting it by the vectoruµ=δµ0; that is,
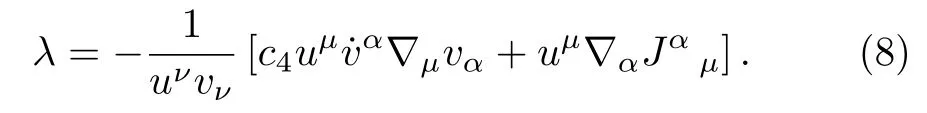
Here we assume thatuνvν≠0 to exclude the trivial zero vector; i.e.,vµ≠0.It is obvious that flat Minkowski metric (ηµν)and a constant null vector (vµ= const.), together withλ= 0, constitute a solution to NAT.The trivial case wherevµ=0 and Ricci flat metrics constitute another solution of NAT.As an example, at each point of a 4-dimensional spacetime it is possible to define a null tetradeaµ=(lµ,nµ,mµ,µ)wherelµandnµare real null vectors withlµnµ=−1, andmµis a complex null vector orthogonal tolµandnµ.The spacetime metric can then be expressed as

This form of the metric is invariant under the local SL(2,C)transformation.For asymptotically flat spacetimes,the metricgµνis assumed to reduce asymptotically to the Minkowski metricηµν,

where (l0µ,n0µ,m0µ,)is the null tetrad of the flat Minkowski spacetime and is the asymptotic limit of the null tetradeaµ= (lµ,nµ,mµ,).Our first assumption in this work is that the null aethervµis proportional to the null vectorlµ; i.e.,vµ=ϕ(x)lµ, whereϕ(x)is a scalar function.In Petrov-Pirani-Penrose classification of spacetime geometries, the null vectorslµandnµplay essential roles.In special types, such as type-D and type-N, the vectorlµis the principal null direction of the Weyl tensor.Hence, with our assumption, the null aether vectorvµgains a geometrical meaning.Physical implications of the aether fieldvµcomes from the scalar fieldϕwhich carries a nonzero charge.Certainly the zero aether,ϕ= 0,or the trivial solution satisfies field equations (4)and (5).To distinguish the nontrivial solution from the trivial one,in addition to the field equations (4)and (5), we impose certain nontrivial initial and boundary conditions forϕ.This is an important point in initial and boundary value problems in mathematics.In any initial and boundary value problem, when the partial differential equation is homogenous,such as the massless Klein-Gordon equation,the trivial solution is excluded by either the boundary or initial conditions.Trivial solution exists only when both boundary and initial values are zero.Therefore, our second assumption in this work is that in stationary problems the scalar fieldϕcarries a nonzero scalar charge and in non-stationary problems it satisfies a non-trivial initial condition.
In the case of black hole solutions and Newtonian approximation,the vector field is taken asvµ=ϕ(x)lµwherelµasymptotically approaches a constant vector andϕ(x)behaves like a scalar field carrying some null aether charge.In the case of the wave solutions,ϕ(x)becomes a massive scalar field.
Null Aether Theory, to our knowledge, is introduced for the first time in this paper.There are some number of open problems to be attacked such as Newtonian limit,black holes,exact solutions,stability,etc.In this work,we investigate the Newtonian limit, the spherically symmetric black hole solutions(inD=4),cosmological solutions,and the AdS wave andpp-wave solutions of NAT.In all these cases, we assume thatvµ=ϕ(x)lµ, wherelµis a null leg of the viel-bein at each spacetime point andϕ(x)is a scalar field defined as the spin-0 aether field that has a mass in general.The covariant derivative of the null vectorlµcan always be decomposed in terms of the optical scalars: expansion, twist, and shear.[47]
3 Newtonian Limit of Null Aether Theory
Now we shall examine the Newtonian limit of NAT to see whether there are any contributions to the Poisson equation coming from the null aether field.For this purpose,as usual,we shall assume that the gravitational field is weak and static and produced by a nonrelativistic matter field.Also,we know that the cosmological constant—playing a significant role in cosmology — is totally negligible in this context.
Let us take the metric in the Newtonian limit as
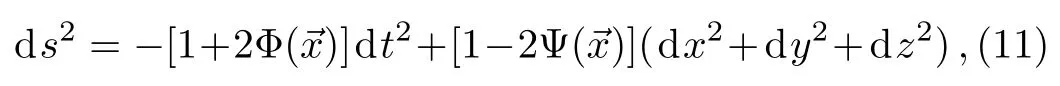
wherexµ=(t,x,y,z).We assume that the matter energymomentum distribution takes the form
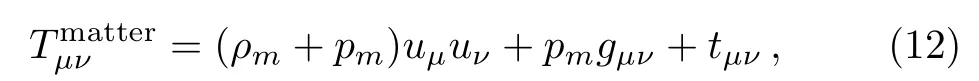
whereandpmare the mass density and pressure of matter, andtµνis the stress tensor withuµtµν=0.We obtain the following cases.
Case 1Let the null vector be

whereaµ= (a0,a1,a2,a3)is a constant null vector representing the background aether andkµ= (k0,k1,k2,k3)represents the perturbed null aether.Nullity of the aether fieldvµimplies
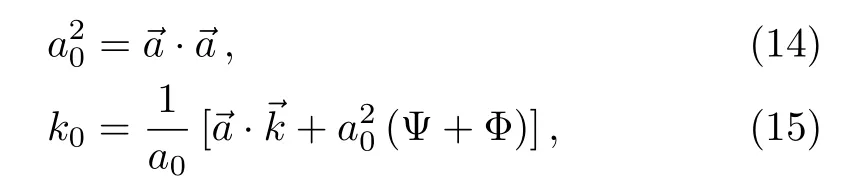
at the perturbation order.Since the metric is symmetric under rotations, we can take, without loosing any generality,a1=a2= 0 and for simplicity we will assume thatk1=k2= 0.Then we obtain Ψ= Φ,c3=−c1,c2=c1,and

It turns out that the gravitational potential Φ satisfies the equation
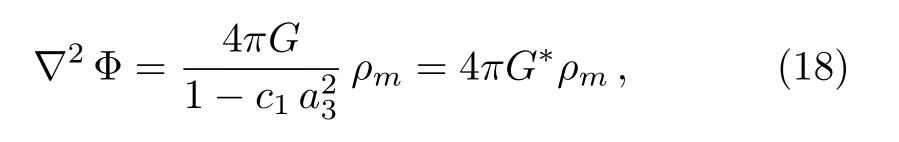
where
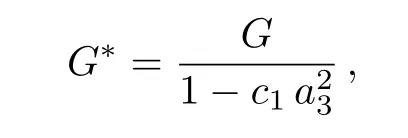
which implies that Newton’s gravitation constantGis scaled as in Refs.[16,42].The constraintc3+c1= 0 can be removed by taking the stress parttµνinto account in the energy momentum tensor, then there remains only the constraintc2=c1.
Case 2In this spacetime, a null vector can also be defined, up to a multiplicative function of, as


which implies that
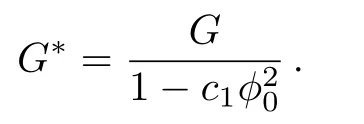
This is a very restricted aether theory because there exist only one independent parameterc1left in the theory.
Case 3The zeroth order scalar aether field in case 2 is zero,ϕ0=0.This means thatϕ()=ϕ1is at the same order as Φ and/or Ψ.In the Eistein-Aether equations (4)and (5), we consider only the linear terms inϕ, Φ, and Ψ.Then the zeroth component of the aether equation (5)gives, at the linear order,

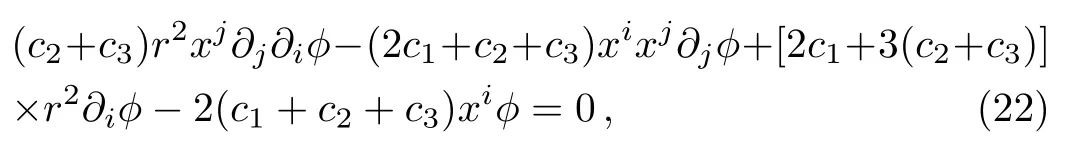
where∇2≡∂i∂i, and thei-th component gives, at the linear order,after eliminatingλusing Eq.(21).Since the aether contribution to the equation (4)is zero at the linear order,the only contribution comes from the nonrelativistic matter for which we have(12).Here we are assuming that the matter fields do not couple to the aether field at the linear order.Therefore, the only nonzero components of Eq.(4)are the 00 and theijcomponent(the 0icomponent is satisfied identically).Taking the trace of theijcomponent produces

which enforces

for the spacetime to be asymptotically flat.Using this fact, we can write, from the 00 component of Eq.(4),

Thus we see that the Poisson equation is unaffected by the null aether field at the linear order inG.
The Poisson equation (25)determines the Newtonian potential.To see the effect of the Newtonian potential on a test particle, one should consider the geodesic equation in the Newtonian limit in which the particle is assumed to be moving nonrelativistically (i.e.,v ≪c)in a static(i.e.,∂tgµν= 0)and weak (i.e.,gµν=ηµν+hµνwith|hµν|≪1)gravitational field.In fact, by taking the metric in the form(11), one can easily show that the geodesic equation reduces to the Newtonian equation of motion d2xi/dt2=−∂iΦ for a nonrelativistic particle.
Outside of a spherically symmetric mass distribution,the Poisson equation(25)reduces to the Laplace equation which gives

On the other hand, for spherical symmetry, the condition(22)can be solved and yields
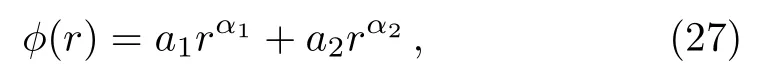
wherea1anda2are arbitrary constants and

This solution immediately puts the following condition on the parameters of the theory

Specifically, whenc1=−9(c2+c3)/8, we have
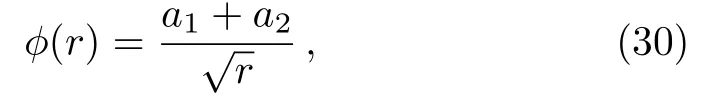
whenc1=0, we have
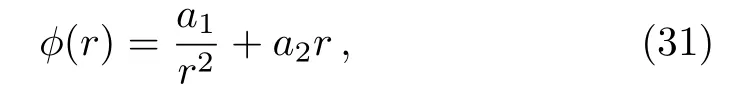
or whenc1=−(c2+c3), we have
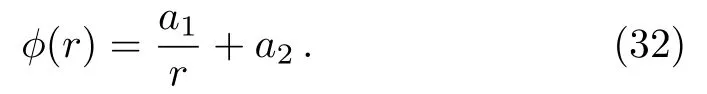
In this last case, asymptotically, lettinga2= 0,limr→∞[rϕ(r)]=a1=G Q, whereQis the NAT charge.
4 Black Hole Solutions in Null Aether Theory
In this section, we shall construct spherically symmetric black hole solutions to NAT inD=4.Let us start with the generic spherically symmetric metric in the following form withxµ=(u,r,θ,ϑ):
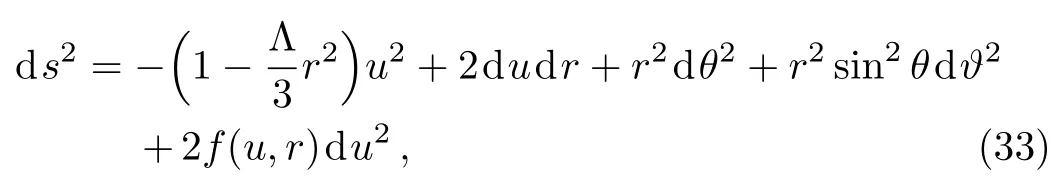
where Λ is the cosmological constant.Forf(u,r)=0,this becomes the metric of the usual (A)dS spacetime.Since the aether field is null,we take it to bevµ=ϕ(u,r)lµwithlµ=δuµbeing the null vector of the geometry.
With the metric ansatz(33), from theucomponent of the aether equation (5), we obtain
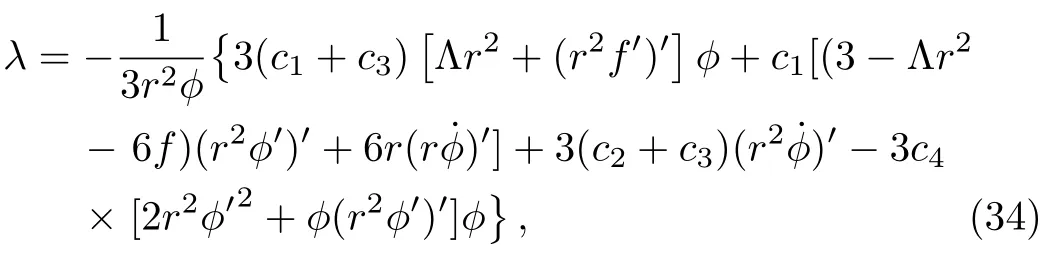
and from thercomponent, we have
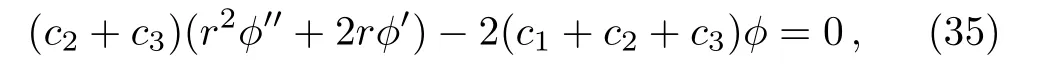
where the prime denotes differentiation with respect torand the dot denotes differentiation with respect tou.The equation(35)can easily be solved and the generic solution is
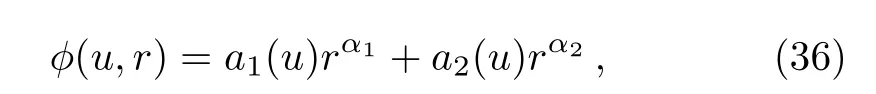
for some arbitrary functionsa1(u)anda2(u), where

When 9+8[c1/(c2+c3)]>0 anda2=0, thenϕ=a1/rαwhereHerea1=GQ,whereQis the NAT charge.
Note that whenc1=−9(c2+c3)/8, the square root in Eq.(37)vanishes and the roots coincide to giveα1=α2=−1/2.Inserting this solution into the Einstein equations(4)yields, for theurcomponent,
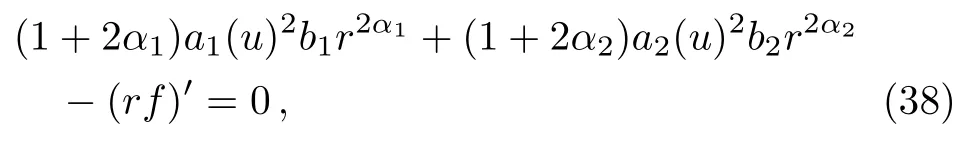
with the identifications
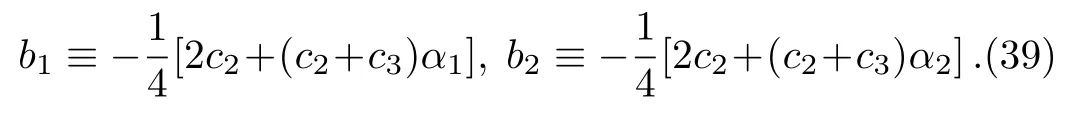
Thus we obtain
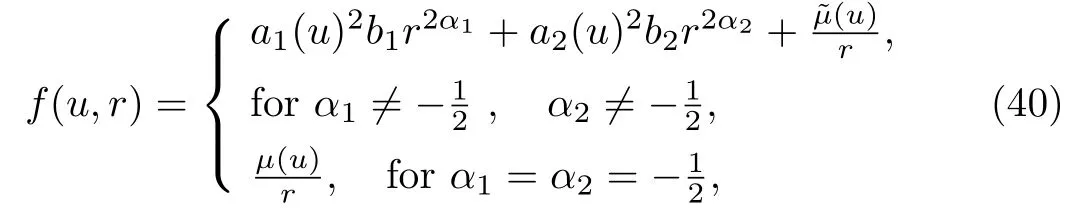
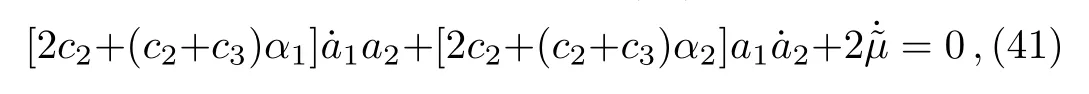
forα1≠−1/2 andα2≠−1/2, and
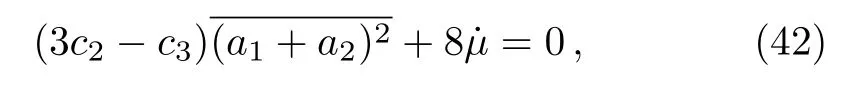
forα1=α2=−1/2.The last case immediately leads to
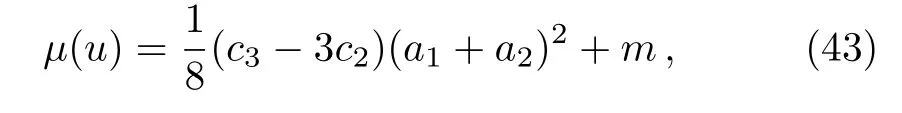
wheremis the integration constant.Thus we see that Vaidya-type solutions can be obtained in NAT without introducing any extra matter fields,which is unlike the case in general relativity.Observe also that whenf(u,r)= 0,we should obtain the (A)dS metric as a solution to NAT(see Eq.(33)).Then it is obvious from Eq.(38)that this is the case, for example, ifα1=α2=−1/2 corresponding to

wheredis an arbitrary constant anda(u)is an arbitrary function.
Defining a new time coordinatetby the transformation
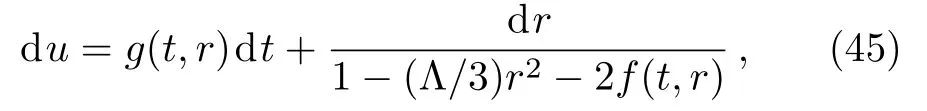
one can bring the metric (33)into the Schwarzschild coordinates
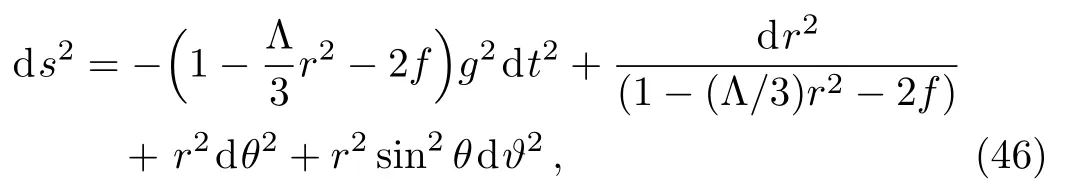
where the functiong(t,r)should satisfy
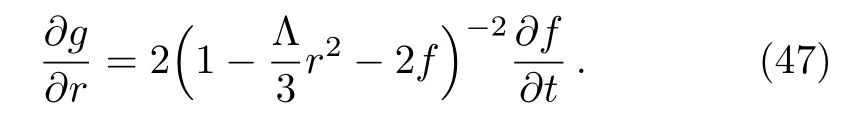
Whena1(u)anda2(u)are constants, sincef=f(r)then,the condition (47)says thatg=g(t)and so it can be absorbed into the time coordinatet, meaning thatg(t,r)can be set equal to unity in Eqs.(45)and (46).In this case, the solution(46)will describe a spherically symmetric stationary black hole spacetime.The horizons of this solution should then be determined by solving the equation
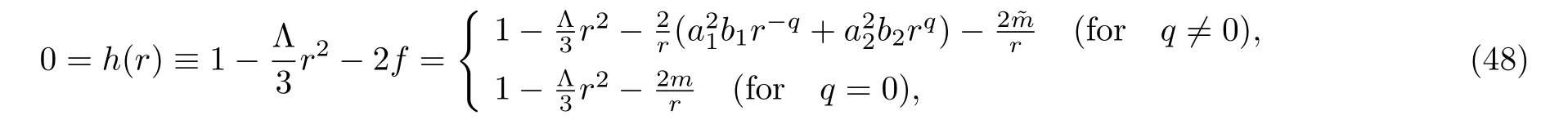

Whena2= 0, we leta1=GQ, and the first case (q≠0)in Eq.(48)becomes
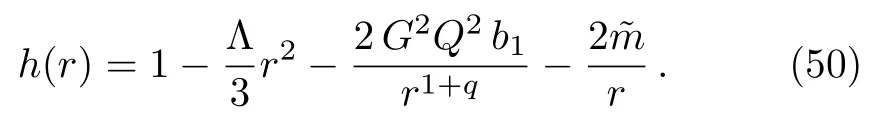
This is a black hole solution with event horizons located at the zeros of the functionh(r)which depend also on the constantQ.This clearly shows that the corresponding black hole carries an NAT chargeQ.The second case(q=0)in Eq.(48)is the usual Schwarzschild-(A)dS spacetime.At this point, it is important to note that whena1anda2are in the order of the Newton’s constantG, i.e.a1∼Ganda2∼G, sinceh(r)depends on the squares ofa1anda2, we recover the Newtonian limit discussed in Sec.3 for Λ=0, ˜m=GMandD=4.For special values of the parameters of the theory, the first case (q≠0)of Eq.(48)becomes a polynomial ofr; for example,
•Whenc1= 0 (q= 3),h(r)≡1−A/r4−Br2−2/r:This is a Schwarzschild-(A)dS type solution ifA=0.Solutions involving terms likeA/r4can be found in, e.g.,Refs.[9,48].
•Whenc1=−(c2+c3)(q=1),h(r)≡1−A −Λr2/3−B/r2−2/r: This is a Reissner-Nordström-(A)dS type solution ifA=0.
•Whenc1=−5(c2+c3)/8 (q= 2),h(r)≡1−Λr2/3−A/r3−Br−2/r: This solution withA=0 has been obtained by Mannheim and Kazanas[49]in conformal gravity who also argue that the linear termBrcan explain the flatness of the galaxy rotation curves.
HereAandBare the appropriate combinations of the constants appearing in Eq.(48).For such cases,the equationh(r)=0 may have at least one real root corresponding to the event horizon of the black hole.For generic values of the parameters, however, the existence of the real roots ofh(r)= 0 depends on the signs and values of the constants Λ,b1,b2, andin Eq.(48).Whenqis an integer, the roots can be found by solving the polynomial equationh(r)=0, as in the examples given above.Whenqis not an integer, finding the roots ofh(r)is not so easy,but when the signs of limr→0+h(r)and limr→∞h(r)are opposite, we can say that there must be at least one real root of this function.Since the signs of these limits depends on the signs of the constants Λ,b1,b2, and ˜m, we have the following cases in whichh(r)has at least one real root:
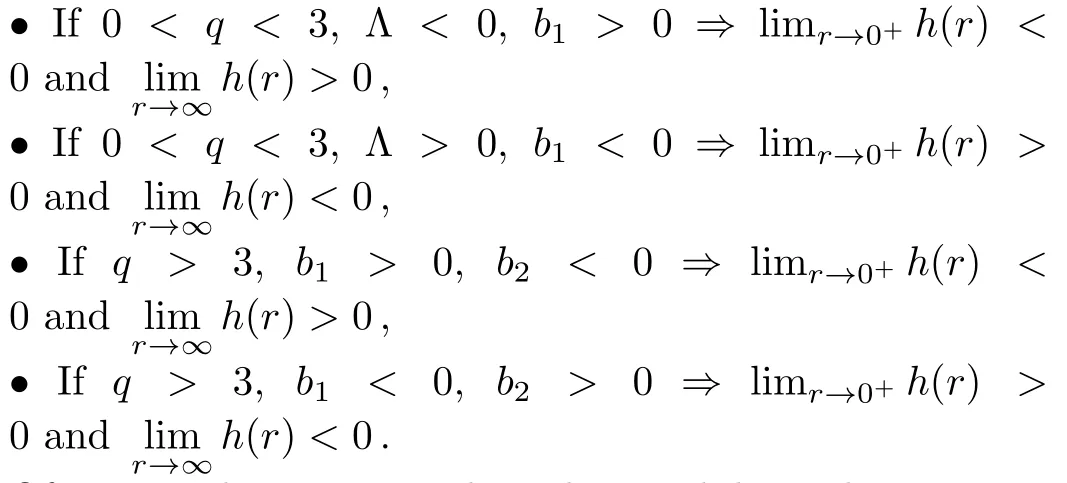
Of course, these are not the only possibilities, but we give these examples to show the existence of black hole solutions of NAT in the general case.
5 Cosmological Solutions in Null Aether Theory
The aim of this section is to construct cosmological solutions to the NAT field equations(4)and(5).We expect to see the gravitational effects of the null aether in the context of cosmology.We will look for spatially flat cosmological solutions, especially the ones which have power law and exponential behavior for the scale factor.
Taking the metric in the standard FLRW form and studying in Cartesian coordinates for spatially flat models, we have
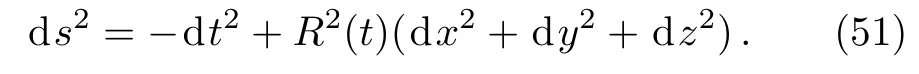
The homogeneity and isotropy of the space dictates that the “matter” energy-momentum tensor is of a perfect fluid; i.e.,

whereuµ=(1,0,0,0)and we made the redefinitions
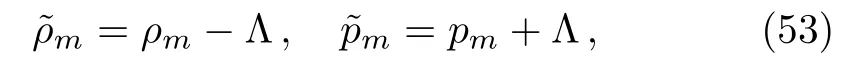
for, respectively, the density and pressure of the fluid which are functions only oft.Therefore, with the inclusion of the matter energy-momentum tensor (52), the Einstein equation (4)take the form
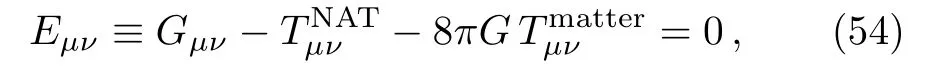
wheredenotes the null aether contribution on the right hand side of Eq.(4).Since first two terms in this equation have zero covariant divergences by construction,the energy conservation equation for the fluid turns out as usual; i.e., from∇νEµν=0, we have
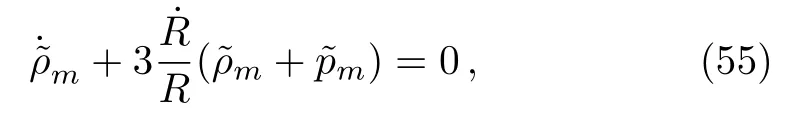
where the dot denotes differentiation with respect tot.
Now we shall take the aether field as

which is obviously null, i.e.vµvµ=0, with respect to the metric (51).Then there are only two aether equations:one coming from the time component of Eq.(5)and the other coming from thexcomponent.Solving the time component for the lagrange multiplier field, we obtain
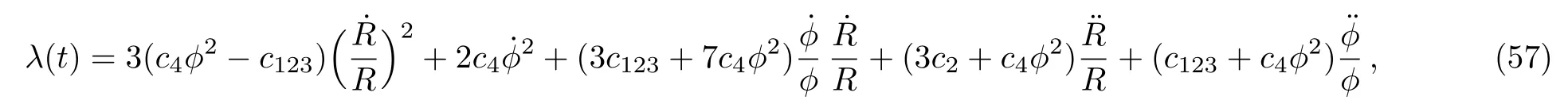
wherec123≡c1+c2+c3, and inserting this into thexcomponent, we obtain
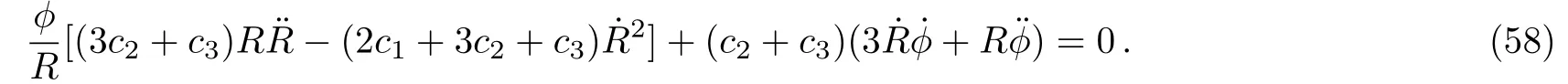
Also, eliminatingλfrom the Einstein equations (54)by using Eq.(57), we obtain

fromEtt=0 andExx=0, respectively, and
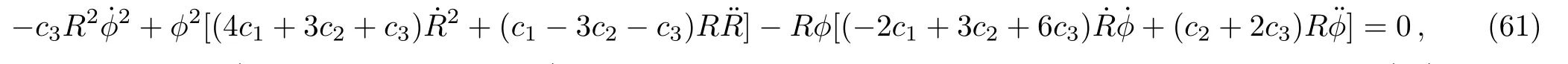
fromExx −Eyy=0 (or fromExx −Ezz=0).TheEtx=0 equation is identically satisfied thanks to Eq.(58).
To get an idea how the null aether contributes to the acceleration of the expansion of the universe, we defineH(t)=(the Hubble function)andh(t)=.Then Eqs.(58)and (61)respectively become
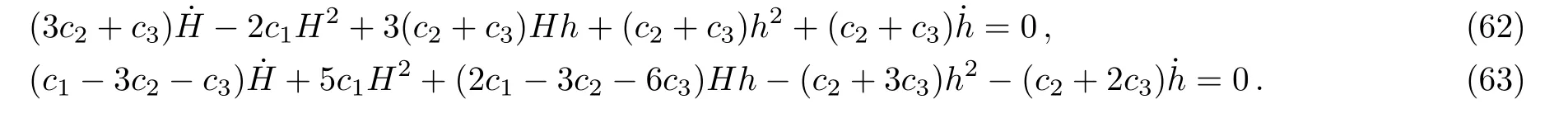
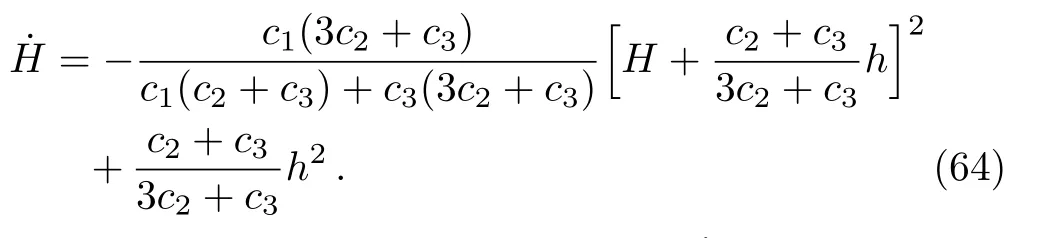
It is now possible to make the sign ofpositive by assuming that
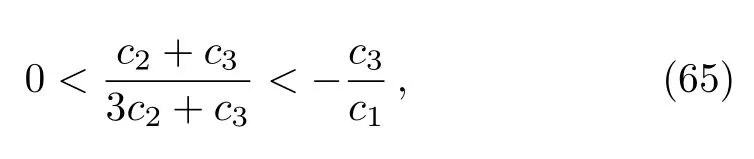
which means that the universe’s expansion is accelerating.
In the following sub-sections we give exact solutions of the above field equations in some special forms.
5.1 Power Law Solution
Let us assume the scale factor has the behavior

whereR0andωare constants.Then the equation (58)can easily be solved forϕto obtain
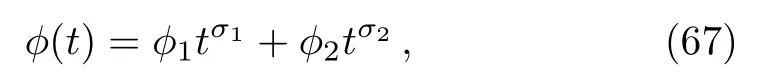
whereϕ1andϕ2are arbitrary constants and

Now plugging Eqs.(66)and (67)into Eq.(61), one can obtain the following condition on the parameters:

where

The interesting cases are
(i)β=0,
(ii)β=1+3ωandϕ2=0,
(iii)β=−(1+3ω)andϕ1=0,
(iv)
Using the definition ofβin Eq.(68),we can now put some constraints on the parameters of the theory.
Case 1(β=0)
In this case, it turns out that
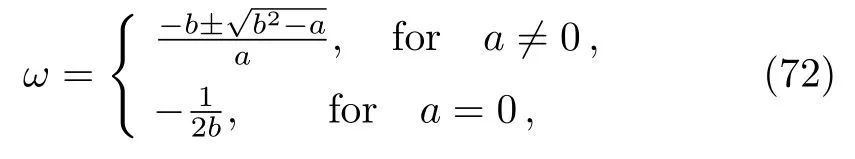
where we define
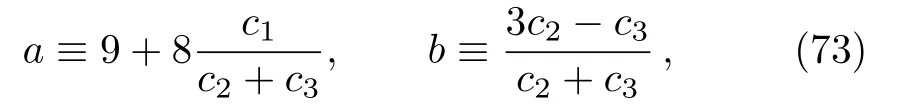
which must satisfyb2−a>0.Then we have
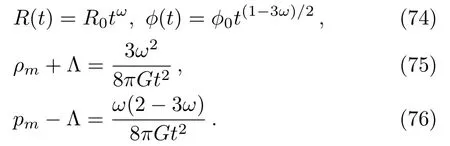
Hereϕ0is a new constant defined byϕ0≡ϕ1+ϕ2.The last two equations say that
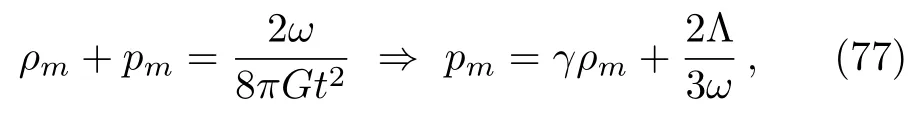
where

Thus,for dust(pm=0)to be a solution,it is obvious that
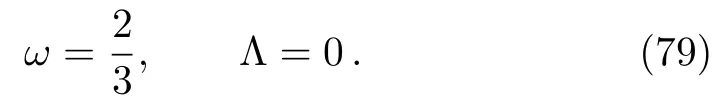
Case 2 and 3(β= 1 + 3ω,ϕ2= 0)and (β=−(1+3ω),ϕ1=0)
In these two cases, we have
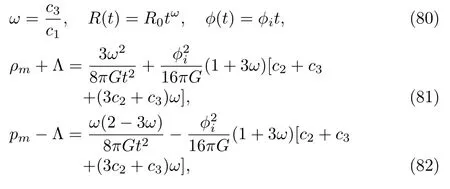
where the subscriptirepresents “1” for Case 2 and “2”for Case 3.Adding Eqs.(81)and (82), we also have
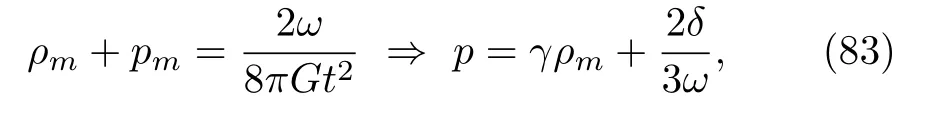
where
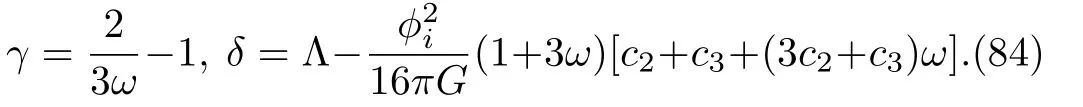
It is interesting to note that the null aether is linearly increasing with time and, together with the parameters of the theory, determines the cosmological constant in the theory.For example, for dust (pm= 0)to be a solution,it can be shown that

Sinceβ >0 by definition(see Eq.(68)),ω >−1/3 in Case 2 andω <−1/3 in Case 3.So the dust solution (85)can be realized only in Case 2.
Case 4 and 5andand
In these cases, using the definition ofβgiven in Eq.(68),we immediately obtain
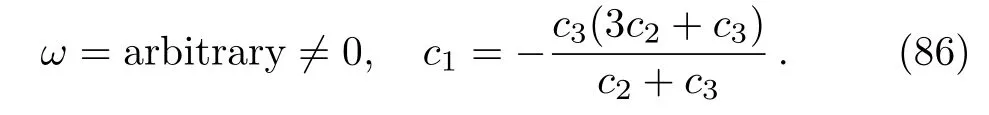
We should also haveβ >0 by definition.Then we find
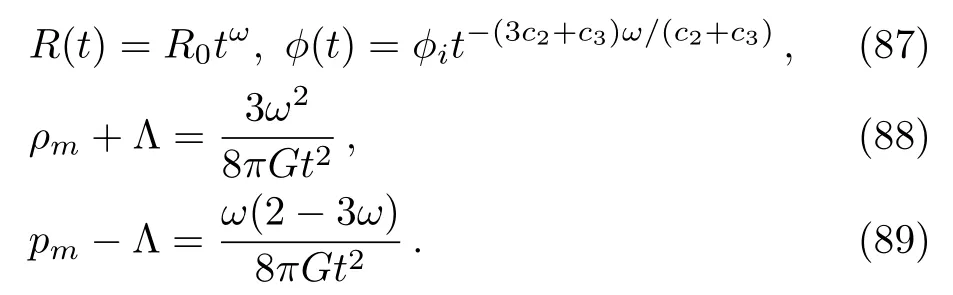
Hereirepresents “2” for Case 4 and “1” for Case 5.So as in Case 1,

where

In all the cases above, the Hubble functionH=w/tand hence ˙H=−w/t2.Thenw <0 corresponds to the acceleration of the expansion of the universe, and in all our solutions above, there are indeed cases in whichω <0.
5.2 Exponential Solution
Now assume that the scale factor has the exponential behavior

whereR0andωare constants.Following the same steps performed in the power law case, we obtain
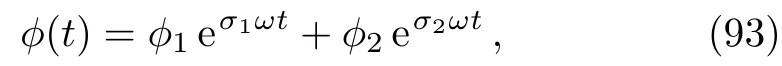
whereϕ1andϕ2are new constants and
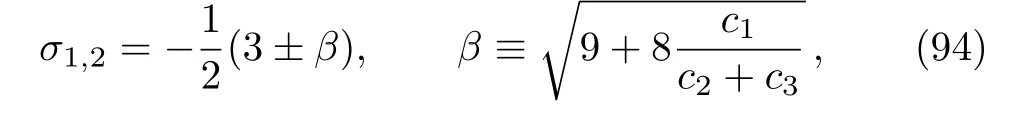
and the condition
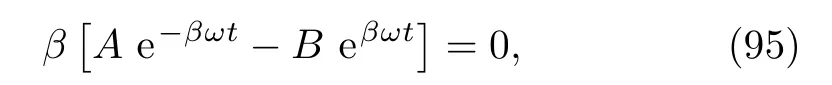
where
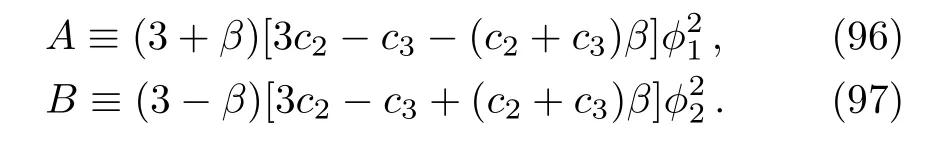
Then the interesting cases are
(i)β=0⇒ ϕ(t)=ϕ0e−3ωt/2,
(iii)
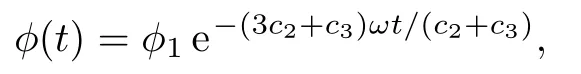
where we definedϕ0≡ϕ1+ϕ2.It should be noted again thatβ >0 by definition (See Eq.(94)).In all these three cases, we find that
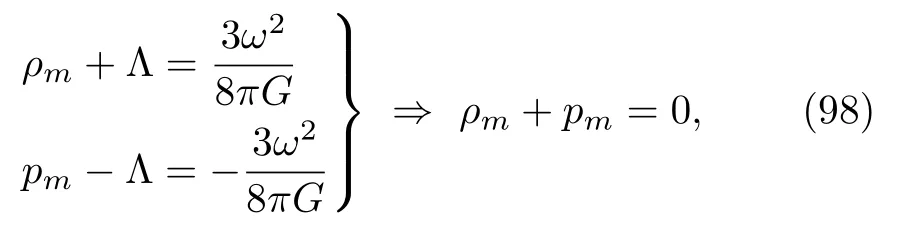
whereωis arbitrary.Whenρm=pm=0,this is the usual de Sitter solution which, describes a radiation dominated expanding universe.
6 Wave Solutions in Null Aether Theory:Kerr-Schild-Kundt Class of Metrics
Now we shall construct exact wave solutions to NAT by studying in genericD ≥3 dimensions.For this purpose, we start with the general KSK metrics[33−38]of the form
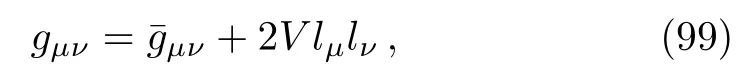
with the properties
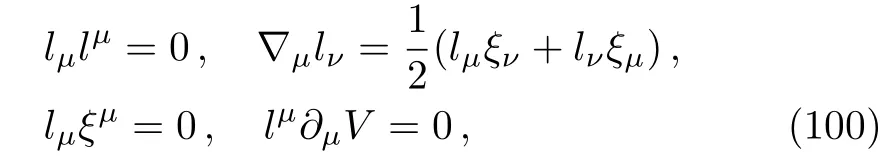
whereξµis an arbitrary vector field for the time being.It should be noted thatlµis not a Killing vector.From these relations it follows that
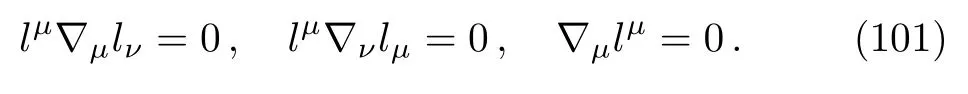
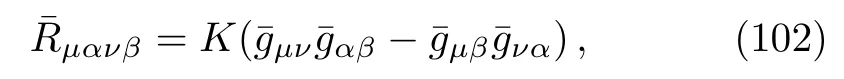
with
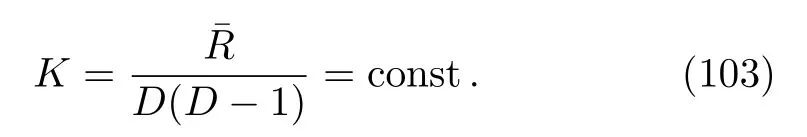
It is therefore either Minkowski, de Sitter (dS), or antide Sitter (AdS)spacetime, depending on whetherK=0,K >0,orK <0.All the properties in Eq.(100),together with the inverse metric

imply that (see, e.g., Ref.[34])
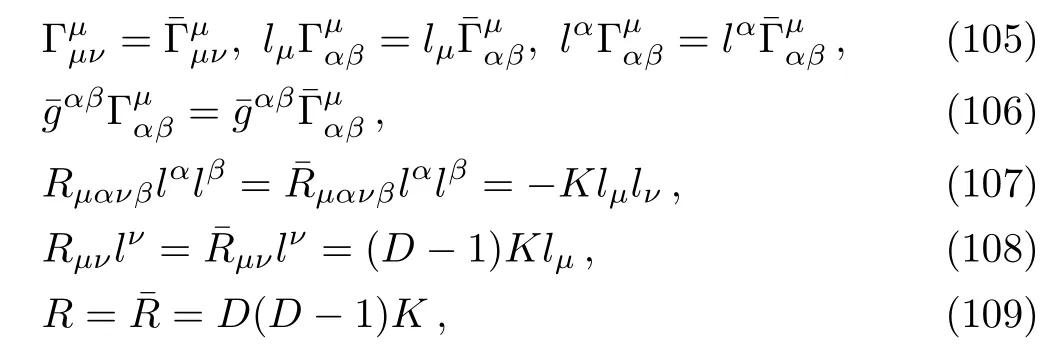
and the Einstein tensor is calculated as
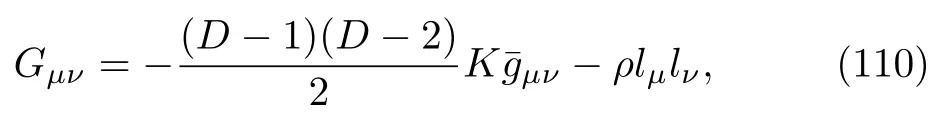
with
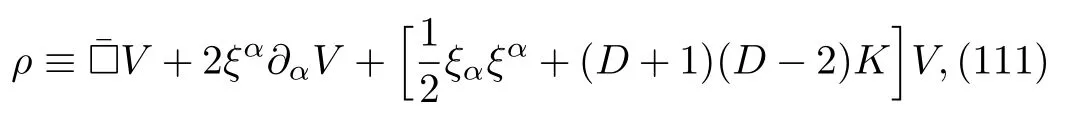
To solve the NAT field equations we now letvµ=ϕ(x)lµand assumelµ∂µϕ= 0.By these assumptions we find that Eqs.(6)and (7)are worked out to be

Then one can compute the field equations (4)and (5)as

where □≡∇µ∇µand use has been made of the identity [∇µ,∇ν]lα=Rµναβlβ.For the KSK metric (99), these equations become
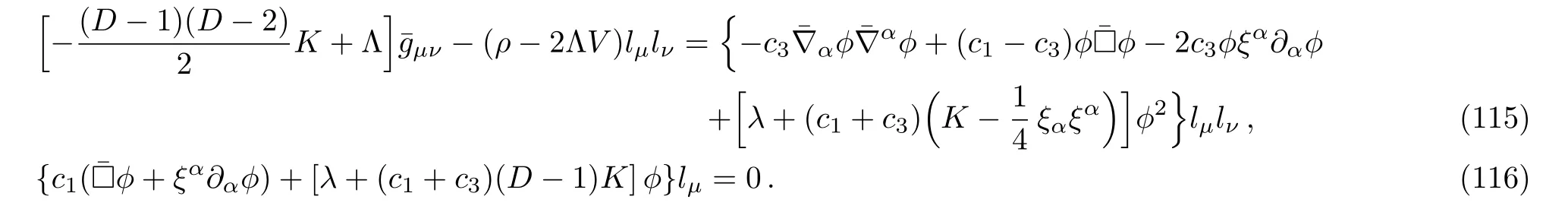
From these, we deduce that
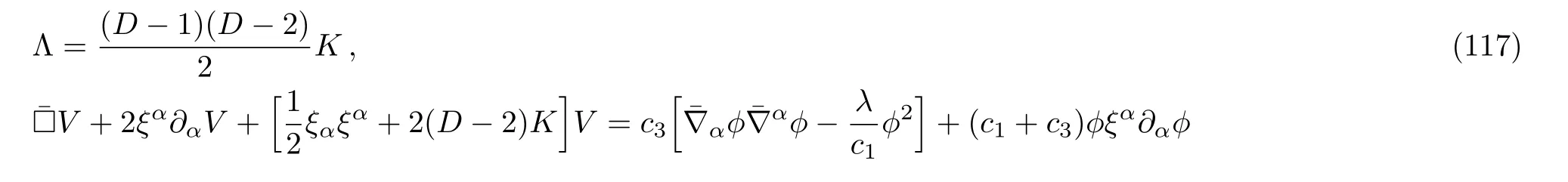
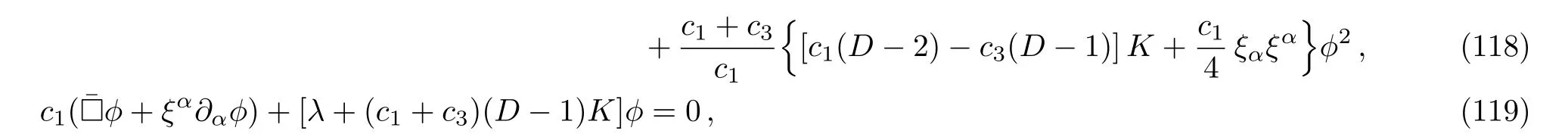
where we eliminated theterm that appears in Eq.(115)by using the aether equation Eq.(119)and assumingc1≠0.
Now let us make the ansatz

for some arbitrary constantα.With this, we can write Eq.(118)as
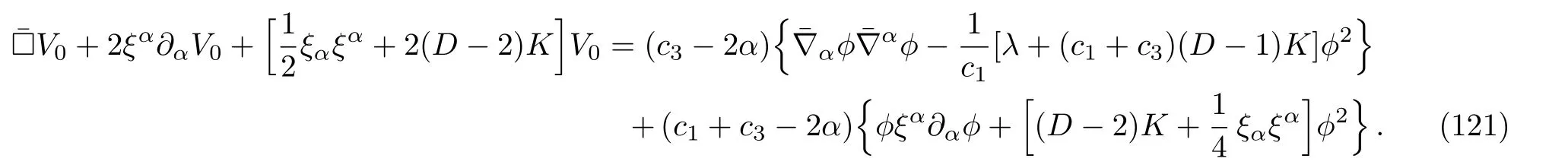
Here there are two possible choices forα.The first one isα=c3/2 for which Eq.(121)becomes
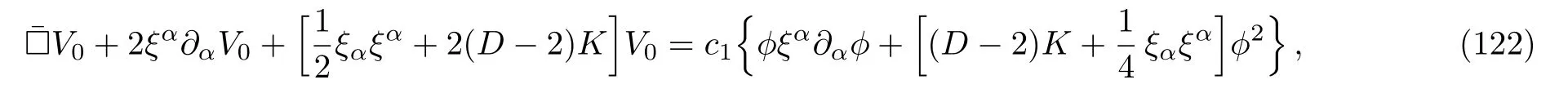
and reduces to

whenK=0 andξµ=0, which is thepp-wave case to be discussed in Sec.8.The other choice,α=(c1+c3)/2, drops the second term in Eq.(121)and produces
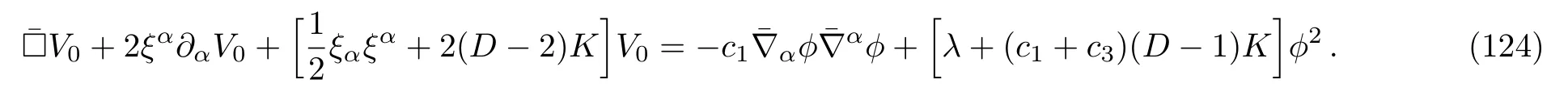
Here it should be stressed that this last case is present only when the background metric is nonflat (i.e.K≠0)and/orξµ≠0.
On the other hand, the aether equation (119)can be written as
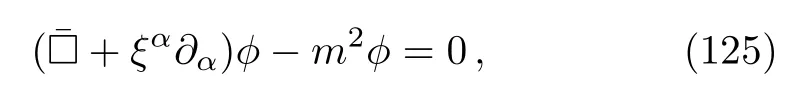
where, assumingλis constant, we defined
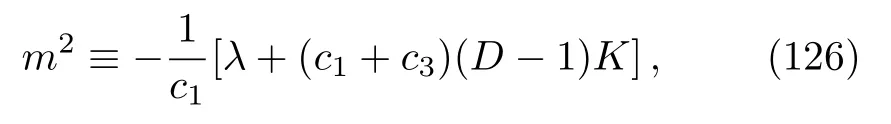
sincec1≠0.The equation (125)can be considered as the equation of the spin-0 aether fieldϕwithmbeing the“mass” of the field.The definition (126)requires that
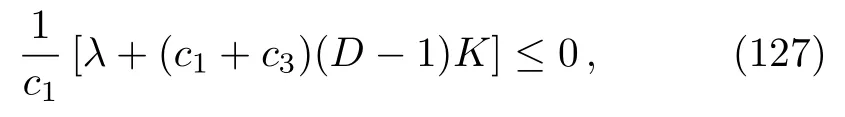
the same constraint as in Eq.(186)whenK= 0.Obviously, the fieldϕbecomes “massless” if
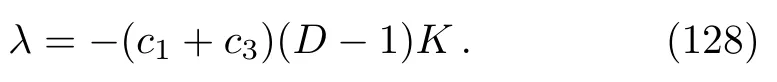
Thus we have shown that, for any solutionϕof Eq.(125),there corresponds a solutionV0of Eq.(122)forα=c3/2 or of Eq.(124)forα=(c1+c3)/2, and we can construct an exact wave solution with nonflat background given by Eq.(99)with the profile function Eq.(120)in NAT.
7 AdS-Plane Waves in Null Aether Theory
In this section,we shall specifically consider AdS-plane waves for which the background metricis the usualDdimensional AdS spacetime with the curvature constant

whereℓis the radius of curvature of the spacetime.We shall represent the spacetime by the conformally flat coordinates for simplicity; i.e.xµ= (u,v,xi,z)withi=1,...,D −3 and
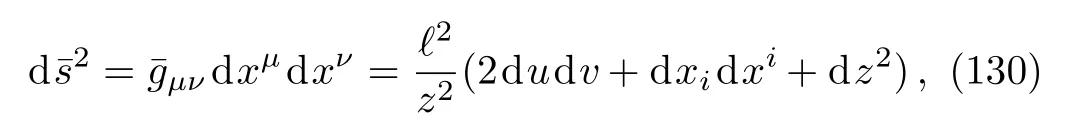
whereuandvare the double null coordinates.In these coordinates, the boundary of the AdS spacetime lies atz=0.
Now if we take the null vector in the full spacetime of the Kerr-Schild form Eq.(99)aslµ=δuµ, then using Eq.(104)along withlµlµ=0,
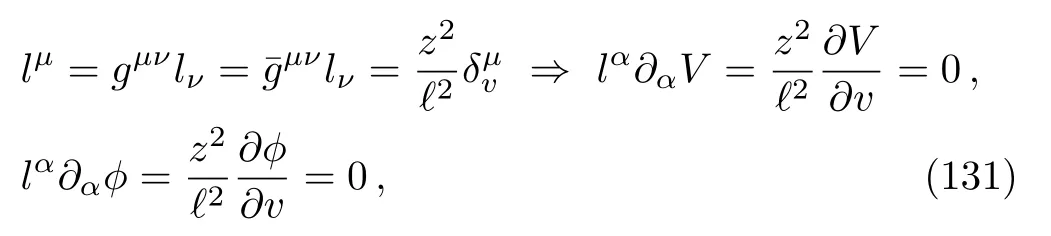
so the functionsVandϕare independent of the coordinatev; that is,V=V(u,xi,z)andϕ=ϕ(u,xi,z).Therefore the full spacetime metric defined by Eq.(99)will be
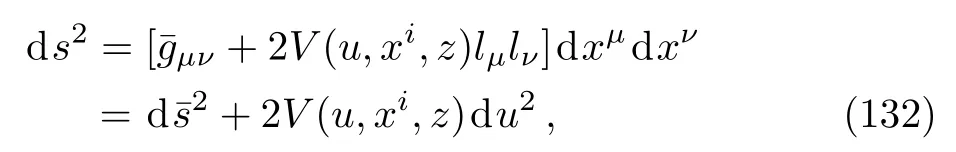
with the background metric (130).It is now straightforward to show that (see also Ref.[34])
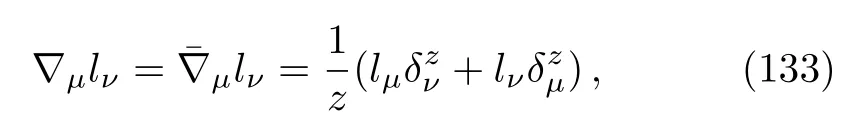
where we used the second property in Eq.(105)to convert the full covariant derivative∇µto the background one, andlµ=δuµwith∂µlν=0.Comparing Eq.(133)with the defining relation in Eq.(100), we see that

where we again used Eq.(104)together withlµξµ=0.
Thus, for the AdS-plane wave ansatz Eq.(132)with the profile function

to be an exact solution of NAT, the equations that must be solved are the aether equation (125), which takes the form
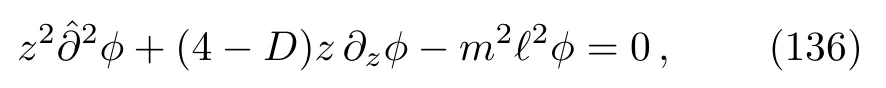
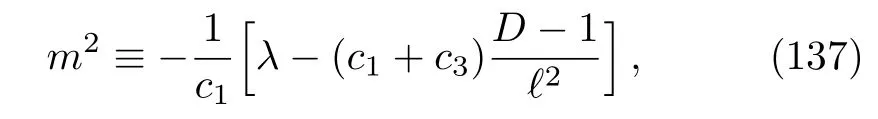
and the equation (122)forα=c3/2, which becomes
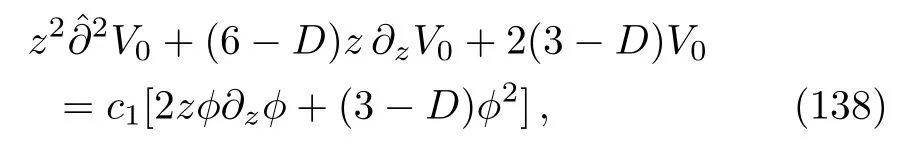
or the equation (124)forα=(c1+c3)/2, which becomes
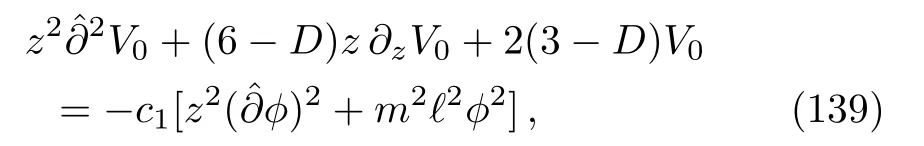
7.1 AdS-Plane Waves in Three Dimensions
It is remarkable that the equations (136), (138), and(139)can be solved exactly inD= 3.In that casexµ= (u,v,z), and so,V0=V0(u,z)andϕ=ϕ(u,z).Then Eq.(136)becomes

with
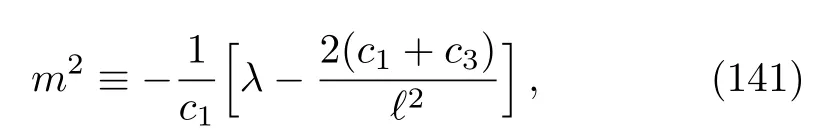
and has the general solution, whenm≠0,
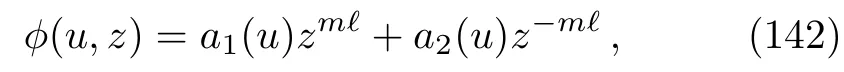
wherea1(u)anda2(u)are arbitrary functions.With this solution, Eqs.(138)and (139)can be written compactly as
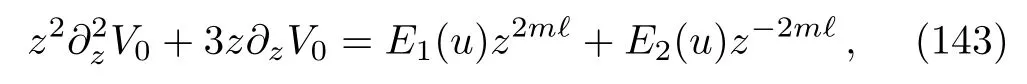
where
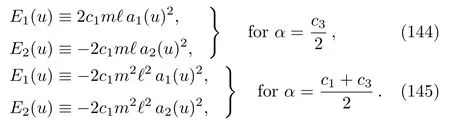
The general solution of Eq.(143)is
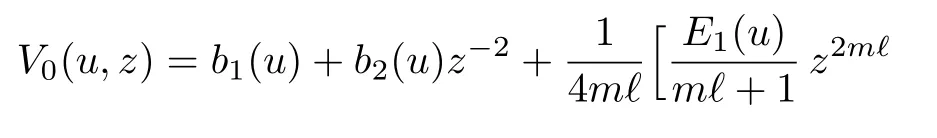

with the arbitrary functionsb1(u)andb2(u).Note that the second termb2(u)z−2can always be absorbed into the AdS part of the metric (132)by a redefinition of the null coordinatev, which means that one can always setb2(u)=0 here and in the following solutions without loosing any generality.In obtaining Eq.(146), we assumed thatmℓ±1≠0.If, on the other hand,mℓ+1=0, then the above solution becomes

and ifmℓ −1=0, it becomes
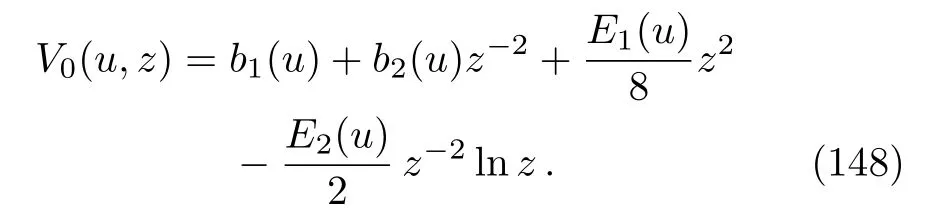
At this point, a physical discussion must be made about the forms of the solutions Eq.(142)and Eq.(146): As we pointed out earlier, the pointz=0 represents the boundary of the background AdS spacetime;so,in order to have an asymptotically AdS behavior as we approachz=0,we should have (the Breitenlohner-Freedman bound[39])

Sinceℓ2= 1/|Λ|in three dimensions, this restricts the mass to the range

which, in terms ofλthrough Eq.(141), becomes
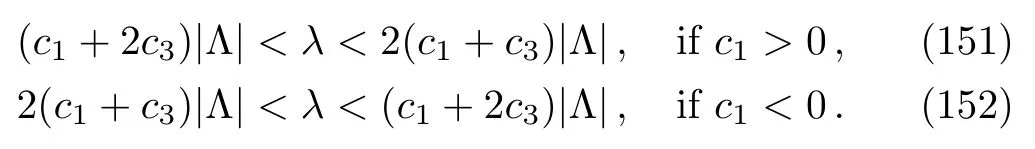
Thus we have shown that the metric

with the profile function
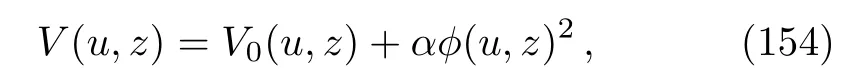
describes an exact plane wave solution,propagating in the three-dimensional AdS background, in NAT.
Up to now, we consider the casem≠0.The casem=0, which corresponds to the choiceλ=2(c1+c3)/ℓ2in Eq.(141), needs special handling.The solution of Eq.(140)whenm=0 is
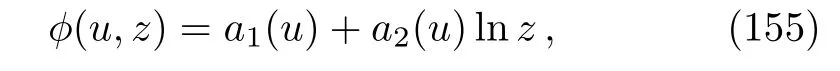
with the arbitrary functionsa1(u)anda2(u).Inserting this into Eqs.(138)and (139)forD=3 produces
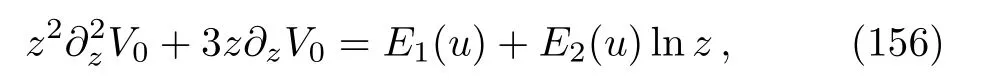
where
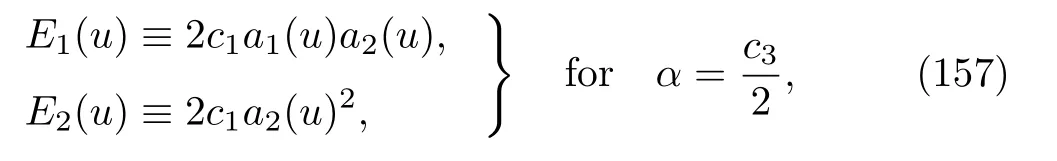
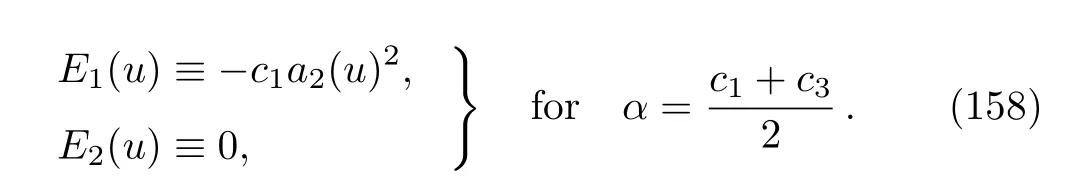
The general solution of Eq.(156)can be obtained as
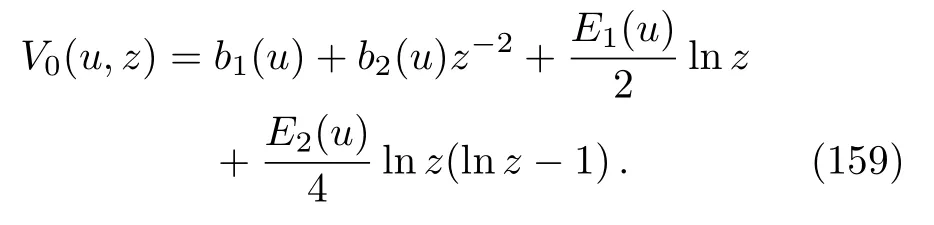
7.2 AdS-Plane Waves in D Dimensions:A Special Solution
Let us now study AdS-Plane Waves inDDimensions:A Special SolutionLet us now study the problem inDdimensions.Of course, in this case, it is not possible to find the most general solutions of the coupled differential equations (136), (138), and (139).However, it is possible to give a special solution, which may be thought of as the higher-dimensional generalization of the previous three-dimensional solution (154).
TheD-dimensional spacetime has the coordinatesxµ= (u,v,xi,z)withi= 1,...,D −3.Now assume that the functionsV0andϕare homogeneous along the transverse coordinatesxi; i.e., take
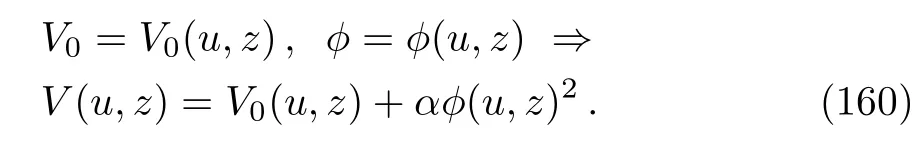
In that case, the differential equation (136)becomes
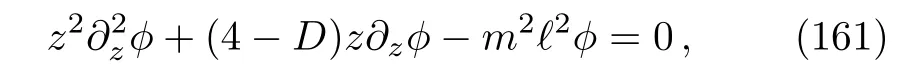
wheremis given by Eq.(137), whose general solution is,forD≠3,
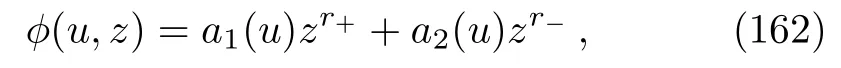
wherea1(u)anda2(u)are two arbitrary functions and
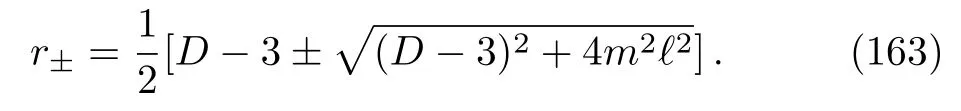
Inserting Eq.(162)into Eqs.(138)and (139)yields
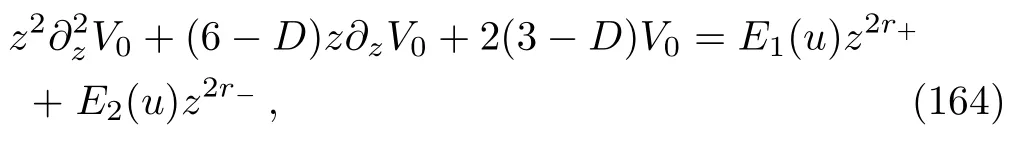
where
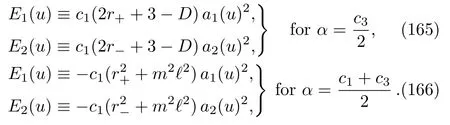
The general solution of Eq.(164)can be obtained as
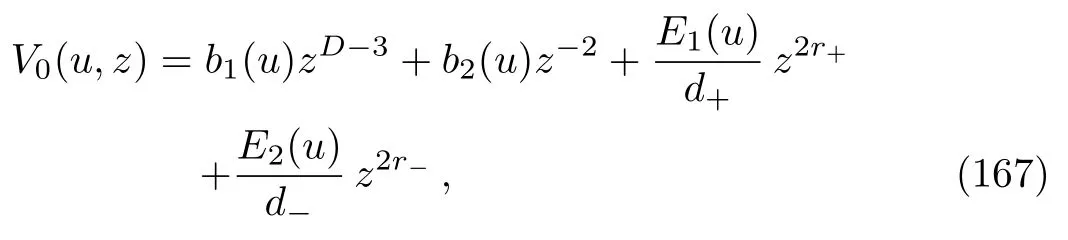
whereb1(u)andb2(u)are arbitrary functions.This solution is valid only if

Whend+=0, we have
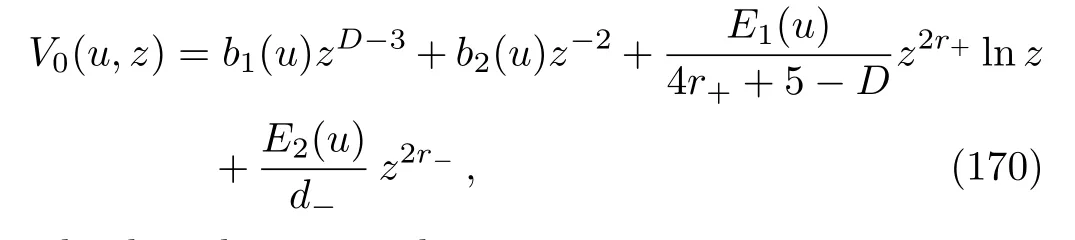
and, whend−=0, we have
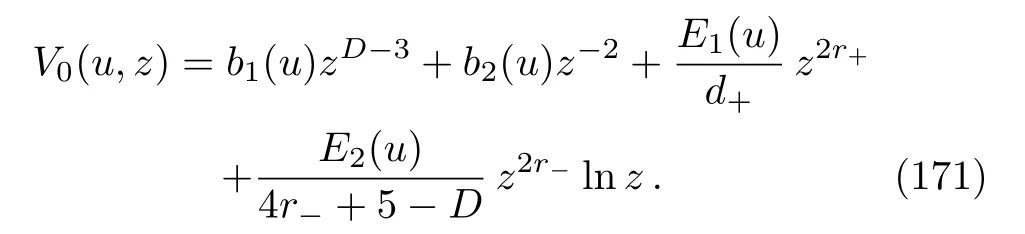
Form≠0,all these expressions reduce to the corresponding ones in the previous section whenD=3.
As we discuss in the previous subsection, these solutions should behave like asymptotically AdS as we approachz=0.This means that

With Eqs.(163)and (129), this condition gives
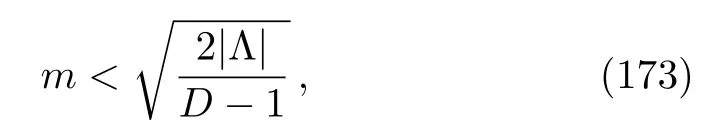
whereD >3.ForD= 4 and taking the present value of the cosmological constant,|Λ| <10−52m−2≈10−84(GeV)2, we obtain the upper boundm <10−42GeV for the mass of the spin-0 aether fieldϕ.
Therefore the metric
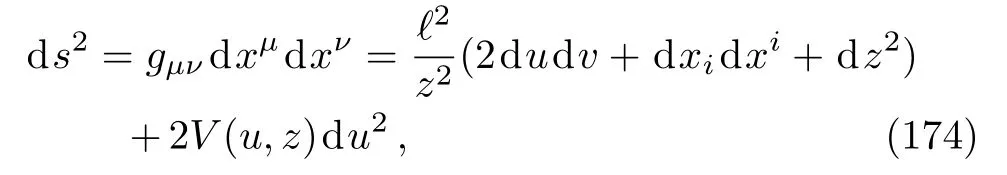
with the profile function
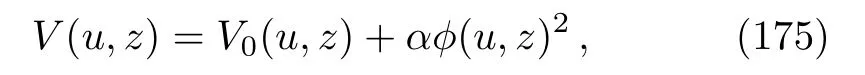
describes an exact plane wave, propagating in theDdimensional AdS background, in NAT.
8 pp-Waves in Null Aether Theory
As a last example of KSK metrics, we shall considerpp-waves, These are defined to be spacetimes that admit a covariantly constant null vector fieldlµ; i.e.,
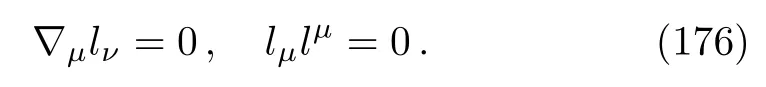
These spacetimes are of great importance in general relativity in that they constitute exact solutions to the full nonlinear field equations of the theory, which may represent gravitational, electromagnetic, or some other forms of matter waves.[47]
In the coordinate systemxµ= (u,v,xi)withi=1,...,D −2 adapted to the null Killing vectorlµ=δuµ,thepp-wave metrics take the Kerr-Schild form[50−51]
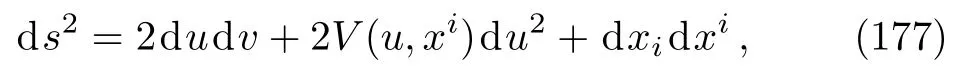
whereuandvare the double null coordinates andV(u,xi)is the profile function of the wave.For such metrics, the Ricci tensor and the Ricci scalar become
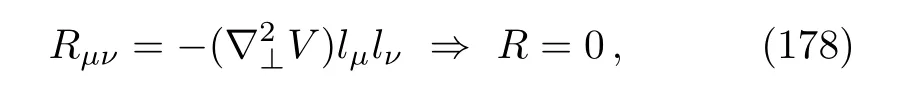
where∇2⊥ ≡ ∂i∂i.A particular subclass ofpp-waves are plane waves for which the profile functionV(u,xi)is quadratic in the transverse coordinatesxi, that is,
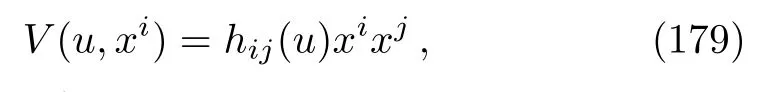
where the symmetric tensorhij(u)contains the information about the polarization and amplitude of the wave.In this case the Ricci tensor takes the form
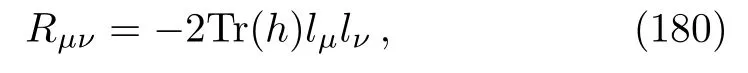
where Tr(h)denotes the trace of the matrixhij(u).
Now we will show thatpp-wave spacetimes described above constitute exact solutions to NAT.As before,we define the null aether field asvµ=ϕ(x)lµ, but this time we let the scalar functionϕ(x)and the vector fieldlµsatisfy the following conditions
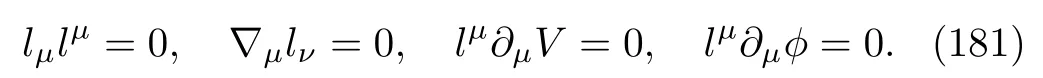
Note that this is a special case of the previous analysis achieved by taking the background is flat (i.e.K= 0)andξµ= 0 there.Then it immediately follows from Eqs.(112), (113), and (114)that

and the field equations are
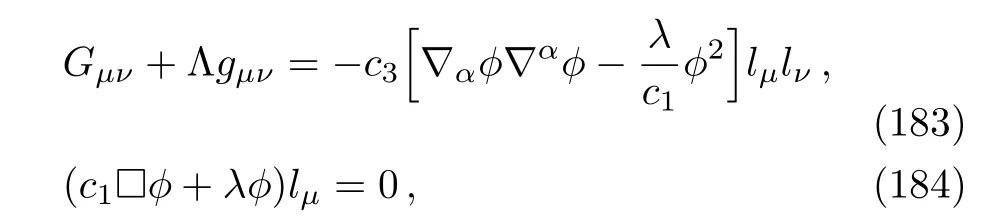
where we have eliminated theϕ□ϕterm that should appear in Eq.(183)by using the aether equation (184)assumingc1≠0.The right-hand side of the equation (183)is in the form of the energy-momentum tensor of a null dust, i.e.Tµν=Elµlνwith

The conditionE ≥0 requires that††
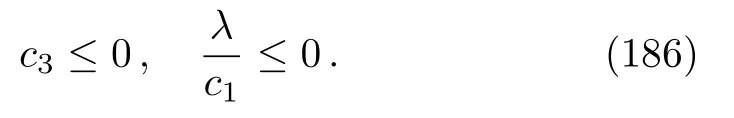
On the other hand,the equation(184)gives Klein-Gordon equation for the fieldϕ(x):

where we defined the “mass” by

which is consistent with the constraint (186).
With thepp-wave ansatz (177), the field equations(183)and (184)become
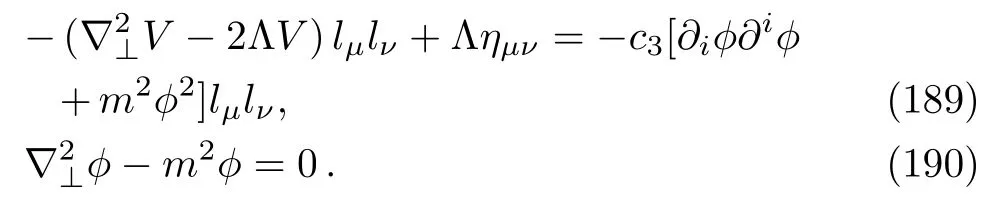
Therefore, the profile function ofpp-waves should satisfy
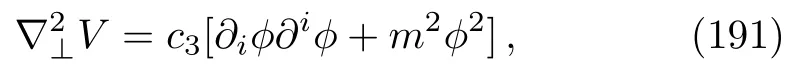
since it must be that Λ= 0.At this point, we can make the following ansatz
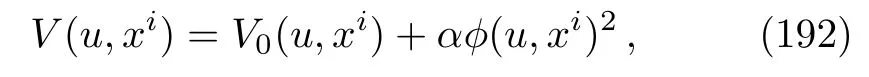
whereαis an arbitrary constant.Now plugging this into Eq.(191), we obtain
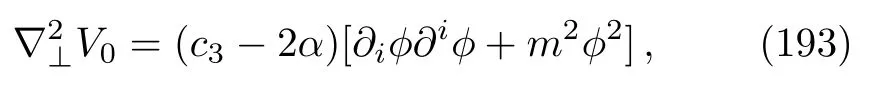
and since we are free to choose any value forα, we get
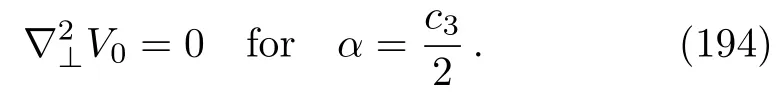
Thus, any solutionϕ(u,xi)of Eq.(190)together with the solutionV0(u,xi)of the Laplace equation (194)constitutes app-wave metric (177)with the profile functionV(u,xi)given by Eq.(192).
Let us now consider the plane wave solutions described by the profile function (179).In that case, we can investigate the following two special cases.
The c3= 0 case
Whenc3= 0 (or,α= 0 through Eq.(194)), it is obvious from Eq.(192)that the functionϕ, satisfying Eq.(190), detaches from the functionVand we should haveV=V0.This means that the profile function satisfies the Laplace equation, i.e.,

which is solved byV(u,xi)=hij(u)xixjonly if Tr(h)=0.Thus we have shown that plane waves are solutions in NAT provided the equation (190)is satisfied independently.For example, in four dimensions with the coordinatesxµ=(u,v,x,y), the metric
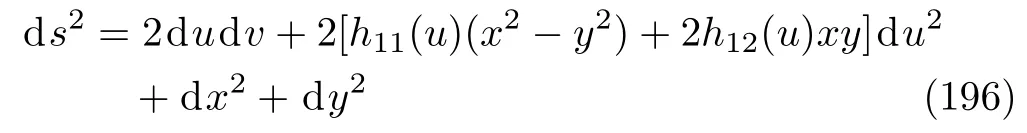
describes a plane wave propagating along the null coordinatev(related to the aether field throughvµ=ϕδµvwithϕ(u,xi)satisfying Eq.(190))in flat spacetime.Here the functionh12(u)is related to the polarization of the wave and, for a wave with constant linear polarization, it can always be set equal to zero by performing a rotation in the transverse plane coordinatesxandy.
††At this point, it is worth mentioning that, although the Null Aether Theory being discussed here is inherently different from the Einstein-Aether theory[2−3]with a unit timelike vector field, the constraintc3≤0 in Eq.(186)is not in conflict with the range given in the latter theory.Indeed, imposing that the PPN parameters of Einstein-Aether theory are identical to those of general relativity, the stability against linear perturbations in Minkowski background, vacuum-erenkov, and nucleosynthesis constraints require that (see, e.g., Ref.[42])

wherec+≡c1+c3andc−≡c1−c3.Thus, for any fixed valuec+in the range 2/3 So there is always a region wherec3is negative; for example, whenc+=4/5, we have−4/15 The c3≠0 and V0(u,xi)= tij(u)xixj case In this case, the Laplace equation (194)says that Tr(t)=0, and from Eq.(192)we have Inserting this into Eq.(190), we obtain This condition is trivially satisfied ifhij=tij, but this is just the previousc3= 0 case in whichV=V0.Nontrivially, however, the condition Eq.(198)can be satisfied by setting the coefficient of the first term and the massm(or,equivalently,the Lagrange multiplierλ)equal to zero.Then again plane waves occur in NAT. In this work, we introduced the Null Aether Theory(NAT),which is a vector-tensor theory of gravity in which the vector field defining the aether is assumed to be null at each point of spacetime.This construction allows us to take the aether field (vµ)to be proportional to one null leg (lµ)of the viel-bein defined at each point of spacetime, i.e.vµ=ϕ(x)lµwithϕ(x)being the spin-0 part of the aether field.We first investigated the Newtonian limit of this theory and then constructed exact spherically symmetric black hole solutions inD= 4 and nonlinear wave solutions inD ≥3 in the theory.Among the black hole solutions, we have Vaidya-type nonstationary solutions, which do not need any extra matter fields for their very existence: the aether behaves in a sense as a null matter field to produce such solutions.Besides these, there are also (i)Schwarzschild-(A)dS type solutions withh(r)≡1−Br2−2m/rforc1= 0 that exist even when there is no explicit cosmological constant in the theory, (ii)Reissner-Nordström-(A)dS type solutions withh(r)≡1−Λr2/3−B/r2−2m/rforc1=−(c2+c3),(iii)solutions withh(r)≡1−Λr2/3−Br −2m/rforc1=−5(c2+c3)/8, which were also obtained and used to explain the flatness of the galaxy rotation curves in conformal gravity,and so on.All these solutions have at least one event horizon and describe stationary black holes in NAT.We also discussed the existence of black hole solutions for arbitrary values of the parameters{c1,c2,c3,c4}. We studied the cosmological implications of NAT in FLRW spacetimes.We assumed the null aether is propagating along thexdirection and found mainly two different types of solutions.In the first type, the null aether scalar fieldϕ(t)and radius functionR(t)are given astσ(power law)whereσis expressed in terms of the parameters of the theory.The pressure and the matter density functions blow up whent=0(Big-bang singularity).The second type is the de Sitter universe with exponentially decaying aether filed.In this case the pressure and the matter density functions are constants.We showed that the accelerated expansion of the universe is possible in NAT if the parameters of the theory satisfy some special inequalities. As for the wave solutions, we specifically studied the Kerr-Schild-Kundt class of metrics in this context and showed that the full field equations of NAT reduce to just two,in general coupled,partial differential equations when the background spacetime takes the maximally symmetric form.One of these equations describes the massive spin-0 aether fieldϕ(x).When the background is AdS,we solved these equations explicitly and thereby constructed exact AdS-plane wave solutions of NAT in three dimensions and in higher dimensions than three if the profile function describing the wave is independent of the transverseD −3 coordinates.When the background is flat, on the other hand, thepp-wave spacetimes constitute exact solutions, for generic values of the coupling constants, to the theory by reducing the whole set of field equations to two decoupled differential equations: one Laplace equation for a scalar function related to the profile function of the wave and one massive Klein-Gordon equation for the spin-0 aether field in (D −2)-dimensional Euclidean flat space.We also showed that the plane waves,subset ofppwaves,are solutions to the field equations of NAT provided that the parameterc3vanishes.Whenc3is nonvanishing,however, the solution of the Laplace equation should satisfy certain conditions and the spin-0 aether field must be massless, i.e.,λ= 0.The main conclusion of these computations is that the spin-0 part of the aether field has a mass in general determined by the cosmological constant and the Lagrange multiplier given in the theory and in the case of AdS background this mass acquires an upper bound (the Breitenlohner-Freedman bound)determined by the value of the background cosmological constant.
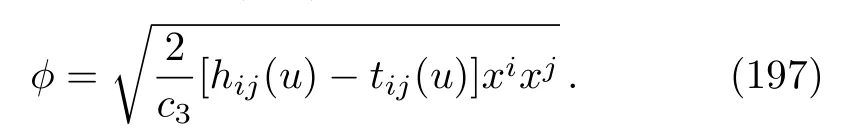
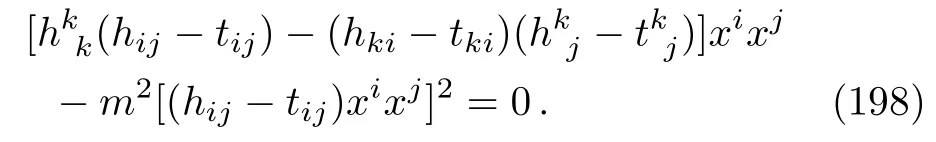
9 Conclusions
杂志排行
Communications in Theoretical Physics的其它文章
- Entropy Quantization of Schwarzschild Black Hole
- Pull-in Instability Analysis of Nanoelectromechanical Rectangular Plates Including the Intermolecular, Hydrostatic, and Thermal Actuations Using an Analytical Solution Methodology
- Boundary Layer Flow over a Curved Surface Imbedded in Porous Medium
- Spin-Dependent Electron Tunneling in ZnSe/Zn1−xMnxSe Heterostructures with Double δ-Potentials
- Interaction of Wave Trains with Defects∗
- Modulated Dust-Acoustic Wave Packets in an Opposite Polarity Dusty Plasma System
