含时滞非线性扩散合作系统的正周期解存在性与全局吸引性∗

艾合麦提·麦麦提阿吉

(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐830046)

0 引言

近年来, Lotka-Volterra系统的动力学行为引起了许多数学家和生物学家的极大关注. 大多数研究工作主要讨论了系统的持续性、持久性、灭绝性、全局稳定性、全局吸引性等问题[1−13]. 众所周知, Lotka-Volterra合作系统是在生物数学和生态数学研究领域中的一类重要相互作用的种群系统[1−5]. 通常大多数种群的环境都会随着时间的变化而发生变化,导致这些种群的生长特征发生变化. 将环境的时间不均匀性纳入模型的方法之一是假设参数是周期性的并且与时间变量的周期相同[6]. 因此, 在大多数情况下, 周期系统的研究价值[2−11]并没有被忽略, 反而在数学生物学和数学生态学的研究领域中发挥了重要作用.

另一方面, 自然界中经常发生时滞现象,许多生态学和生物学模型都可以被表述为具有时滞的微分方程. 目前, 时间尺度上的动力学方程的研究引起了许多学者的兴趣[1−13]. 对于这种类型的系统, 最重要的问题之一是分析时滞对系统稳定性和持久性的影响.

Chen在文献[1]中研究了以下系统

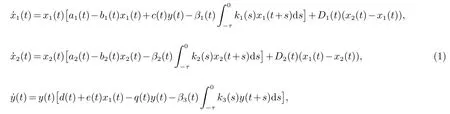
其中x1(t), y(t)是第一个斑块中的种群x和y在时刻t的密度,x2(t)是第二个斑块中的种群x在时刻t的密度, 种群y仅限于在第一个斑块, 种群x可以在第一个斑块和第二个斑块之间扩散,Di(t)(i=1,2) 是种群x在时刻t的扩散系数. 在文献[1]中,模型不仅包括分散过程,还包括系统的一些过去状态. 该文献研究了空间和时间延迟因素对系统稳定性的影响并得到了种群的持续性和系统全局稳定性的充分条件.

在本文中，我们将系统(1)推广到以下非线性扩散系统

通过应用重合度理论[14]和Lyapunov函数方法得到周期系统的正周期解的存在性与全局吸引性的充分条件. 最后给出了一个例子, 通过例子我们证明了所得到结论的正确性.

1 预备知识

在系统(2)中,x1(t), y(t)是第一个斑块中的种群x和y在时刻t的密度,x2(t)是第二个斑块中的种群x在时刻t的密度,种群y仅限于在第一个斑块, 种群x可以在第一个斑块和第二个斑块之间扩散,Di(t)(i=1,2) 是种群x在时刻t的扩散系数. 对于系统(2), 始终假设

(H1)ai(t)(i=1,2), d(t) 是ω-周期连续函数满足是非负ω-周期连续函数,ki(t)(i=1,2,3) 是定义在[−τ,0]的非负可积函数, 且满足条件

在本文中, 假设系统(2)满足下面的初始条件:

其中φi(s)(i=1,2) 和φ(s) 是定义在[−τ,0]上的满足条件φi(0)>0(i=1,2), φ(0)>0 的非负连续函数. 在本文中, 对于任何一个ω-周期连续函数f(t) 使用以下记号

现在, 给出一个重要的定义

定义1称系统(2)是全局吸引的如果系统(2)的任意的两个解(x1(t),x2(t),y(t))和(u1(t),u2(t),v(t))满足

此外, 我们还将用到如下一些引理.

为了得到系统(2)的正ω周期解的存在性.我们将使用文献[14]中的重合度定理.为了读者的方便，下面我们引入重合度定理.

引理1[14]设Ω ⊂X是有界开集,L是指标为零的Fredholm 映射，N 在Ω 上L−紧，假设

则算子方程Lx=Nx在DomL∩至少存在一个解.

关于指标为零的Fredholm算子，连续算子以及连续投影等方面的定义和概念可在文献[2-4]中找到.

引理2[15]设f是定义在[0,∞)上的一个非负函数使得在[0,∞)上可积并且在[0,∞)上一致连续，则

2 主要结论

定理1假设(H1)成立且

则系统(2)至少存在一个正ω-周期解.

证明对系统(2)作变换

则系统(2)可变为

为了应用引理1,下面给出具有范数||·|| 的Banach 空间X和Z. 令C(R,R3) 表示全体连续函数u(t)=(u1(t),u2(t),u3(t)):R →R3的空间. 我们取

和

显然,X和Z都是具有范数||·||的Banach 空间. 我们定义线性算子L:DomL⊂X→Z和连续算子N:X→Z如下

和

其中

进一步,我们定义连续投影P:X→X和Q:Z→Z如下

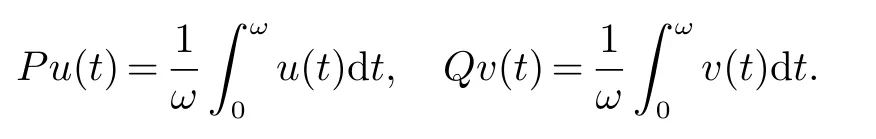
使得v(t) =v1(t)+v2(t), 则有codimImL= 3. 因此,L是一个指标为零的Fredholm 映射. 此外,L的广义逆Kp: ImL→KerP∩DomL为

为了方便, 我们记F(t)=(F1(t),F2(t),F3(t)) 其中

于是我们有

和

由(8)和(9), 我们很容易看出QN和Kp(I−Q)N是连续算子. 此外, 由有界和利用Arzela-Ascoli 定理,可以证明对任意有界开集Ω ⊂X是紧的.因此,N对任意有界开集在上是L-紧的.

下面需要寻找一个适当的满足引理1条件的有界开集Ω ⊂X.

对应于算子方程Ly(t)=λNy(t) ,λ∈(0,1), 有

其中Fi(t) (i=1,2,3) 在方程(7)中给定.

假设u(t)=(u1(t),u2(t),u3(t))∈X是系统(10)关于某个λ∈(0,1) 的一个解.把系统(10)从[0,ω]积分, 得到

由(11), 我们有

对每一个i=1,2,3, 我们有

其中Γi(t)是ω周期连续函数. 由(12) 和(13), 我们有

由定理1的假设和(14)可以得到

由u(t)=(u1(t),u2(t),u3(t)) 的连续性,存在常数ξi,ηi∈[0,ω](i=1,2,3) 使得

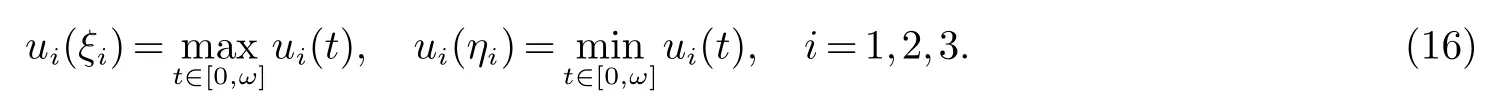
由(16), 我们进一步得到

另一方面, 由(12), (13) 和(16) 得到

由定理1的假设和(16),(18)我们得到

由(11), (13) 和(15) 得到

由(17),(19) 和(20)-(22), 我们有

和

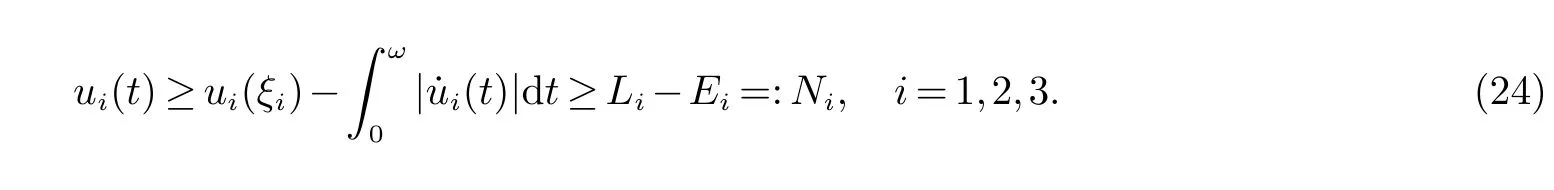
因此, 由(23) 和(24) 我们有

显然,Hi(i=1,2,3) 是与λ∈(0,1) 选取无关的. 对任意u=(u1,u2,u3)∈R3和(6)我们有

其中

我们考虑下面的代数方程组

选取一个足够大的H>0 使得我们定义一个有界开集Ω ⊂X如下

显然, Ω满足引理1的条件(a)和(b). 另外,我们可以直接计算得到

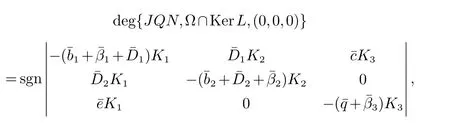
其中Ki=exp{ui}(i=1,2,3).由于

由此, 我们最后得到

这就得到了Ω满足引理1的条件(c).因此系统(5)至少有一个周期解从而系统(2)至少有一个正ω-周期解

关于系统(2)正周期解的存在性和全局吸引性, 我们有下面的结论.

定理2设定理1的全部条件成立, 则系统(2)存在一个全局吸引的正周期解.

证明由定理2 的条件可知系统(2)存在一个正周期解. 设是系统(2) 的一个正周期解.(x1(t),x2(t),y(t)) 是系统(2) 的任意一个正解. 定义Liapunov 函数

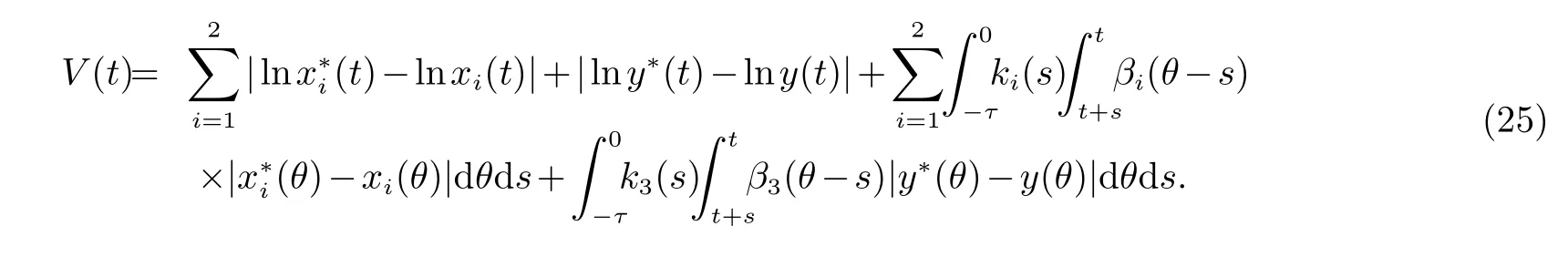
则沿着系统(2) 计算V(t) 的右上导数我们得到

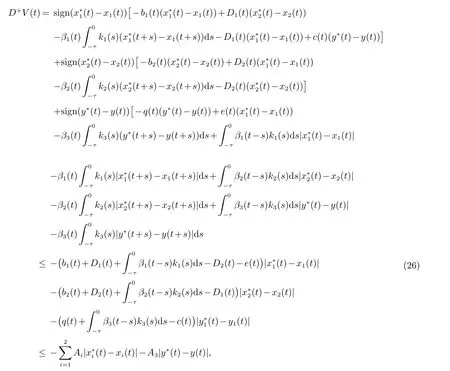
其中Ai(i=1,2,3) 是在定理1中给定的. 由(26)我们得到

其中η=min{Ai(i=1,2,3)}. 在区间[0,t]上积分(27), 我们得到

从而

由V(t)定义和(28),我们得到

因此, 对i=1,2 我们有

由(31) 和(32), 我们有

和

由(28), (33), (34) 我们可以得到xi(t)(i=1,2)和y(t) 对一切的t≥0是有界的,则xi(t),y(t) 和的导数和在区间[0,+∞)上有界的. 从而和它们导数在区间[0,+∞)上有界的.因此在区间[0,+∞)上是一致连续的,由引理2 我们得到

所以,

推论1假设定理2全部条件成立, 则系统(2)是持久的.

证明由系统(2)的全局吸引性可以得到系统(2)的持久性.

注1由定理1,定理2和推论1 可以得到只要系统(2)存在一个正周期解, 那么此正周期解是全局吸引的且系统(2)是持久的结论.

3 例子

例1我们考虑下面的系统

直接计算我们得到

显然,系统(35)的系数满足定理1全部条件. 其数值模拟见图1.

图1 系统(35)的动力学行为Fig 1 Dynamics of System (35)

从数值模拟图1可以看到,系统(35)有一个全局吸引的正周期解并且系统(35)是持久的.