基于DME/DME导航的实际导航性能计算

黄龙杨，郑 晴

(中国民用航空飞行学院 空中交通管理学院，四川 广汉618307)

0 引言

随着民航业的不断发展，航班量不断增加，对于如何解决空域拥挤、提高航班正点率成为业界研究的重点课题。与此同时，国际民航组织ICAO对节油、增加经济效益、环境保护、飞行安全等方面的要求促使我国重点发展基于性能导航(PBN)。实际导航性能(ANP)反映了机载导航系统的定位精度，是PBN运行中的重要概念，可有效监视与告警机载导航性能是否符合RNP应用的必要安全水平。孙淑光等[1]人提出了一种组合导航系统的ANP实时评估方法；赖际舟等[2]人在其基础上运用数值积分逐步逼近95%概率误差圆的方式进行了ANP评估，解决了积分近似函数收敛快的问题；姚鑫雨等[3]人基于“北斗二代”卫星导航系统，提出了一种适用于全球导航系统GNSS的ANP评估方法。

王丹等[4]人基于对VOR/DME、DME/DME定位误差的研究，提出了两种导航方式下飞机实际导航性能计算方法，该方法中，将实际导航性能ANP视为1 σ误差椭圆转换因子k与长半轴的初等函数，但由于转换因子k随椭圆扁率增大而变小 ，因此可能使得误差概率不足95%，影响结果的准确性。VOR导航系统误差较大，主要作为备份导航。为此，本文针对DME/DME陆基导航系统，提出一种改进的ANP计算方法，可有效简化其计算过程。

1 DME系统的测量均方误差

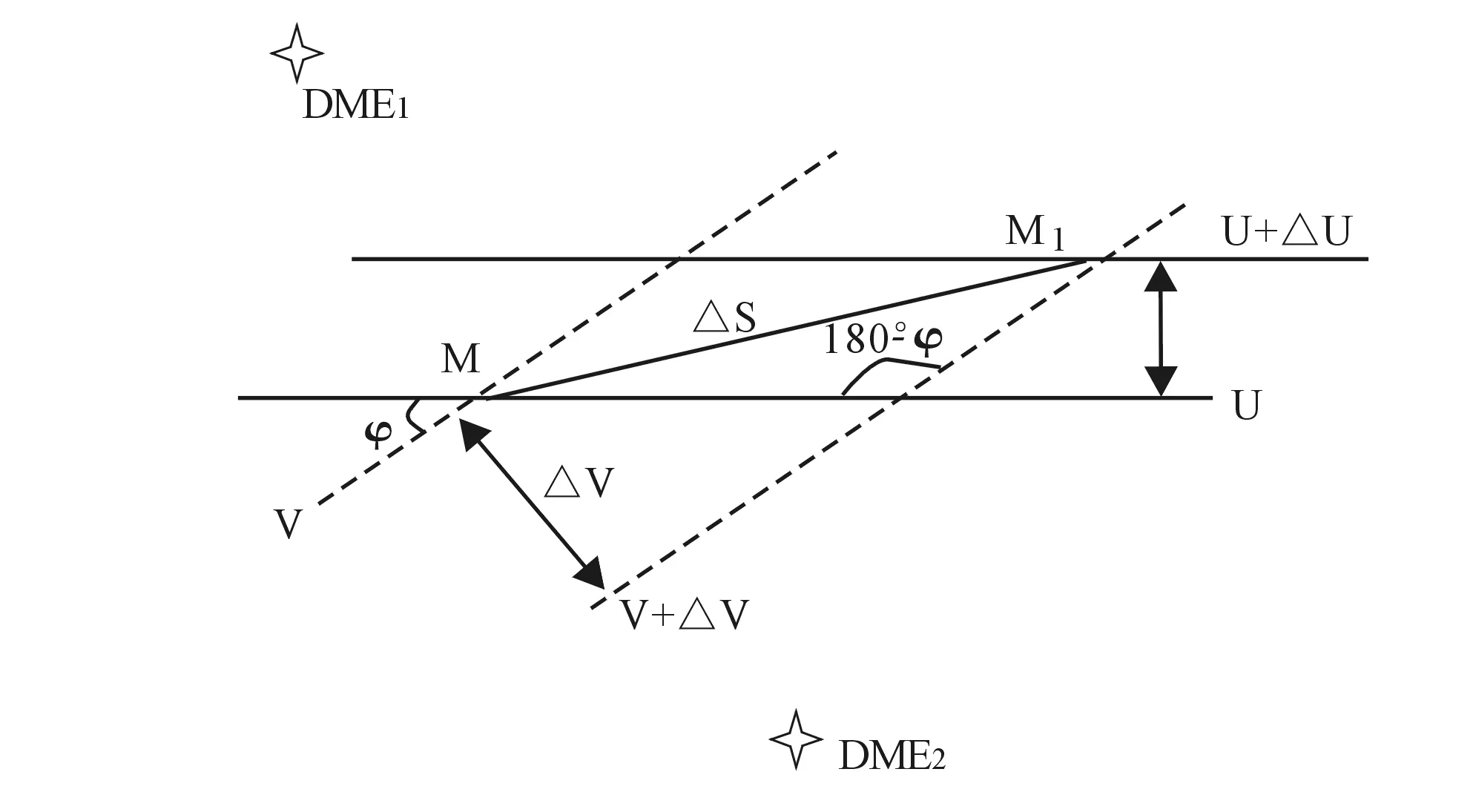
图1DME/DME定位误差的标量表示

1.1 DME/DME方式下定位线误差

DME测量的距离是飞机与地面信标台之间的斜距，而实际导航定位时需要的是飞机与地面DME台之间的水平距离。通常，航空器与地面信标台的连线与水平面的夹角小于8°时，斜距与水平距离差值不会超过1%，此时可认为两者近似相等。只有当航空器保持较高的飞行高度接近DME台时，斜距和水平距离之间才会出现较大的差距，但在区域导航中根据DME/DME的覆盖原理以及选台准则，不会出现此种现象。因此，本文将所测斜距作为水平距离计算。实际中，DME/DME系统定位误差区域由四条弧线围成，由于弧线长度相对于飞机与地面信标台DME1与DME2的水平距离υ、μ很小，故将其理想化为直线，对于分析其区域误差的影响极小，所以可将实际的弧线四边形近似为图1 DME/DME定位误差的标量表示中的平行四边形。Δν、Δμ分别为DME1、DME2的位置线误差，φ为DME1与DME2和飞机测量线的夹角。

航空器测得位置M1与真实位置M之间存在误差Δs，根据余弦定理，有：

Δμ、Δv为零均值随机变量，则Δs的方差可表示为：

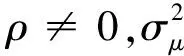
航空无线电技术委员会(Radio Technical Commission for Aeronautics，RTCA)指出[5]，1989年1月1日之后安装的系统，DME系统的测量误差低于0.2海里，因此为保险起见，本文采用其误差容限：

1.2DME/DME方式下定位误差标准差σ的计算

《区域导航所需导航性能最低航空系统性能标准》[5]中提出，若所选组合导航系统的位置线处于覆盖范围边缘时，DME/DME方式下定位误差标准差σ的计算表达式为:

2 ANP的计算

通常，水平面误差x、y为随机误差，服从二维正态分布，其概率密度函数为：

其中，μx、μy为x、y的均值，σx、σy为x、y的方差，ρ1为水平误差的相关系数。

图2 二维正态分布图 图3 xoy面上的投影

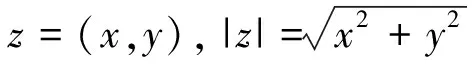
得其原函数为：

z=2.447σ(9)

其计算结果与孙淑光等[1]在机载组合导航系统实际导航性能计算方法的研究中结果相同，且该计算过程更简便。

最后得出：

3 仿真验证

为评估基于DME/DME导航的飞机实际导航性能，选取京沪区域导航航路为背景，基于WGS-84坐标系，进行飞机实际导航性能分析，“北京-上海”飞行航路信息如表1，航路点信息图如图4。导航台对的选取应满足：(1)飞机到导航台的水平距离L满足3海里< L<160 海里；(2)导航台与飞机连线的夹角σ满足30°< σ<150°，共选取15个DME导航台，导航台位置信息图如图5。仿真飞行轨迹水平曲线及航路中选取的DME台对分布示意图如图6。其中，五角星表示航路点，圆点表示所选取的DME导航台。

表1 “北京-上海”飞行航路信息

图4航路点信息图

图5导航台位置信息图

图6飞行轨迹水平曲线及航路中选取的DME台对分布示意图

图7 “北京-上海”航路飞机实际导航性能

图8常规方法与本文方法计算的误差圆概率

图9 DME/DME测量夹角与ANP值的关系

在Matlab环境下对这段航路数据进行仿真计算，“北京-上海”航路飞机实际导航性能结果如图7，其ANP结果数值范围为[0.71,0.96]，符合RNP-2区域导航要求。常规方法与本文方法计算的误差圆概率如图8所示，可知，文献[4]使用的常规计算方法得到的误差圆概率大部分时间低于95%，最小可至90%，而本文提出的适用于DME/DME陆基导航系统的ANP算法能够使误差圆概率较稳定地保持在95% 。

DME/DME测量夹角与ANP值的关系如图9，其中测量交角的骤变过程对应着所选地面台的变化。ANP的值在90°交角时取到最小值，远离90°位置，ANP值增大。

针对误差圆计算不准的问题，姚鑫雨等[3]运用Gauss三点公式结合复化Simpson公式对95%误差圆进行了求解，仿真时间为5702 s，该算法对y区间进行n等分，对f(X,Y)需要进行3×(n+1)次计算，结果有效保证了实际导航性能计算的准确性，运算时间为5.4 s。本文仿真时间为7845 s，运算时间为4.6 s，可知采用本文方法之后可以进一步提高运算速度。

4 结语

基于DME/DME的区域导航是我国主要的导航方式之一。飞机实时导航性能的评估是确保区域导航性能满足RNP需求的关键。本文基于DME/DME导航定位误差分析，对飞机实际导航性能评估方法进行了研究与改进，提高运算速度的同时能够使ANP误差圆概率较稳定地保持在95%，适用于DME/DME导航系统的机载导航性能评估，且方法简单。