借助直观，沟通联系，理解关系——《比的认识》教学新探

■浙江省杭州市余杭区教育学院 张 敏 ■浙江省杭州市余杭区临平三小 周 芳

在《比的认识》教学中按照“两个数相除又叫两个数的比”来教，我遇到一些困惑的问题：1.学生对于“两个数相除又叫两个数的比”认识很牵强,学生并不能自己去发现。2.学生不能感受同类量的比和不同类量比的联系,同类量的比可以得出它们的倍数关系,但不同类量的比表示的不是倍数关系。3.在理解比的意义时,学生用除法来理解比较困难。4.在讨论比分是不是一个比时,学生比较难用“两个数相除”来解释,因为他们认为比分之间也可以存在倍数关系。分析产生这些问题的根源在于教学中用“两个数相除又叫两个数的比”来理解比。因此，我想利用浙教版教材“比表示两个数的一种关系”进行教学，并且要突出是一种对应关系，主要想要突破的问题：1.如何引导学生体会发现比表示两个数的对应关系?2.如何把比与除法,不同类量的比和同类量的比建立联系?

一、基于旧知，提出问题

黑板上出示：△△ ○○○○○○

师：你能比一比吗？这是我们以前学的比多少和倍比,这节课我们还是要来研究比。关于比，你想知道什么？生：比表示什么意思？为什么要用比？怎么比？师：你见过比吗？生：篮球赛的比分，奶粉配方成分比……

根据学生已有经验引出比,并请学生提出研究的主要问题,有利于知识的建构,培养学生提出问题的能力。

二、基于学生经验和直观图认识同类量比的对应关系

（一）认识比的各部分名称

（板书4∶1）这个“：”叫做比号，比号前的数叫前项，比号后的数叫后项。

（二）初步认识比的意义

1.画图理解4∶1表示的含义。

师：老师也带来了一个比，泡果珍饮料中，水和果珍粉的比是4∶1。

水和果珍粉的比是4∶1 , 表示什么意思? 可以怎么分配水和果珍，你能想办法用画图来表示吗?学生根据画的图解释含义。

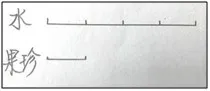
师：如果果珍变化，水该怎么变化？同学们可以讨论。

师：你们发现什么？生：都是水4份配果珍1份。师：4份水配1份果珍，数学上我们可以叫做对应。（板书“对应”）生：水都是果珍的4 倍。师：（板书4÷1=4倍）4是这个比的比值。（板书比值）这个比值表示什么意思呢？ 原来比值中也隐藏着对应关系。

2.认识其他同类量比的含义。

师：这里的4∶1 表示4 份对应1 份，其他的比又表示什么呢？

PPT出示：喷水池的长宽比3∶2（板书3∶2）

公园里花卉面积与草坪面积的比是1∶2（板书1∶2）

师：同桌说说这些比表示的含义？（同桌互说后反馈）

在上述同类量比的认识中借助直观，理解比表示一种对应关系是这节课的创新之处。首先，利用学生已有的经验，让学生通过画图理解同类量的比，即几份配几份，自然引出几份对应几份。其次，让学生借助图，在意义解构活动中感悟对应关系的深层次意义——当两个数量变化时，比可以表示两者之间不变的关系。用图比用具体数更能让学生感悟两者之间不变的关系。没有用抽象的语言或者复杂的教学，只是在图上按照比进行添或减，是具有函数色彩的数学活动。再者，创新了比值的教学，引导学生认识比值可以看成两个数量的一般对应关系：即一份对应几份。而其他具体的比是特殊的对应关系。利用图理解比的意义，并根据比变化图，这是引导学生认识基于一般对应关系的特殊对应关系。利用图可以比较简约、一目了然地把对应关系显示出来。

三、借助图进一步认识不同类量比的对应关系,沟通两种比的联系

（一）认识《总价与数量》的比

PPT出示“6元钱买了2包饼干,总价和数量的比如何表示?”

生：6∶2(板书6∶2）师：这个比表示什么意思？还可以怎么买？请你画一画。

（根据学生的图让学生解释意义。）

师：请观察这些不同买法，你发现有什么相同？

（二）认识《路程和时间》的比

师：汽车在路上行驶50km用了2小时，路程和时间的比是？比值是？生：50∶2，25千米/每小时。师：这个比和比值分别表示什么意思？我们来比较一下，这些比和前面的那些比，相同在哪里？

（学生边说，师边动态出示图）

不同类量的比是以前教学的困惑之处,但是改进教学后用“比表示一种对应关系”就把同类量的比和不同类量的比联系起来。学生根据生活经验和对同类量比的认识，理解不同类量的比是一种对应关系就比较容易了。非常有意思的是，学生在画图中感悟到不同类量的比，用不同的符号来表示不同的量，但学生同样还是在画图、观察比较中体会比的对应关系的内涵。对不同类量比值的进一步探究，把同类量比和不同类量的比进行进一步的联系，即都是一份对应几份。教学中发现学生对不同量的比值的理解较同类量比值的理解更容易些。

四、利用反例进一步明晰比的意义

（PPT 出示）足球比赛甲乙两队进球数的比是2∶1（板书：甲∶乙2∶1）

这个比和我们今天认识的比一样吗？ 你还是可以画图来解释。

师：（学生交流后反馈）是不是今天的比？为什么？

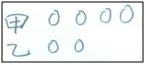
生：我们认识的比表示对应关系,而比分不能表示对应关系,比如比分不是2分对应1分增加的，可能会变成2∶2，所以比分不是今天我们研究的比。

在讨论比分是否是比的环节，我发现用不同的教材教，学生的表现有很大的不同。用“两个数相除又叫两个数的比”来教，由于学生对比本质内涵没有深入体会，只是模糊知道两个数相除是比，所以在讨论中学生不能利用比的本质来解释。在理解比是一种对应关系后，学生就能用假如是对应关系和实际中的比分变化两方面来推理说明。通过这样的反例让学生借助直观，充分说明辨析的过程，明晰概念，培养能力。

五、基于深入体会的抽象概括

师：研究了这么多比，你知道几比几表示的意思了吗？请你自己写一个比，和同桌说一说这个比表示的意思。学生同桌交流后汇报。

学生借助直观，利用已有经验，在自主探究中逐步发现比的本质内涵，逐步抽象概括，相比第一次课中学生对“两个数相除又叫两个数的比”模糊的认识，到这里明确认识比是一种对应关系。其次，利用比值的认识，把比与除法建立了联系——除法是求比值的方法。因为比值是表示每一份对应几，所以就要用除法计算比值，也进一步与除法的意义建立联系。

纵观整节课，我们以整体的眼光，以比是表示一种对应关系将同类量的比和不同类量的比系统认知，并借助对比值的认识进一步把联系更深入。同时借助比值把比与除法的关系自然联系。在比的对应关系的理解中，并不仅仅浮于表面的认识，而是在学生借助图，围绕大问题“这个比表示什么意思，根据这个比可以怎么取？”开展自主探究活动，在观察、比较、讨论中发现对应关系中的函数对应思想。