基于图论组合优化的RGV动态调度模型

魏殿恩　邵翰乔　靳瑾

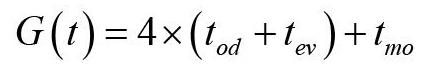
摘   要：随着工业发展对智能化需求的日益增长，RGV小车在运输及仓储方面的应用也越来越广泛，如何以最优路径调度成为了当前需要解决的重要问题。本文针对无故障的一道工序加工情况，选取一道工序加工情况中的一个生产周期为研究对象，将RGV工作系统抽象为路径网络，并利用图论中最短路径的知识求得一道工序物料加工的最优路径。

关键词：RGV动态调度  图论  最优路径

中图分类号：TP18                                   文献标识码：A                        文章编号：1674-098X（2019）10（c）-0079-02

一个智能加工系统是由8台计算机数控机床、1辆轨道式自动引导车、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备组成的。RGV，即轨道式导引小车，国内一般称为穿梭小车或者穿梭车，是一种在车间或者自动化立体仓库中沿着轨道运行的物料运送工具[1]。该小车是一种无人驾驶、能在固定轨道上自由运行的智能车。它根据指令能自动控制移动方向和距离，并自带一个机械手臂两只机械手爪和物料清洗槽，能够完成上下料及清洗物料等作业任务。

1  动态调度

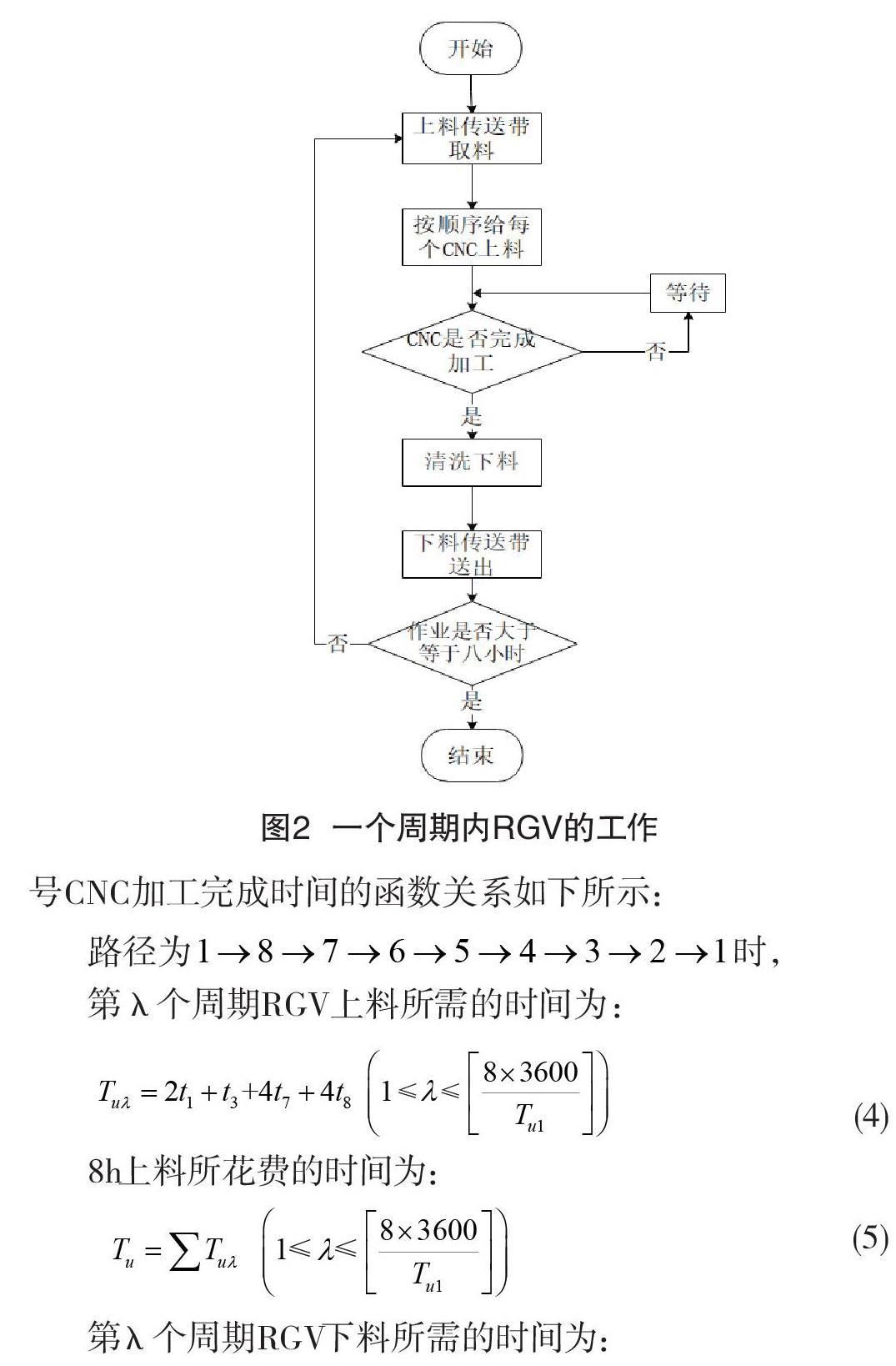
将系统中固定在轨道两侧的CNC抽象为路径网络中的节点，其中将RGV轨道式引导小车简化为一个质点。根据先来先服务的调度准则[1]，将第一轮上料顺序理想简化作为先上料后下料的顺序。将8台CNC上下料一次完整的过程看作为一个周期。为了使RGV的效率最高，拟定关于RGV一个周期内运作时间t的函数如下所示。

已知RGV小车为奇数序号和偶数序号的CNC上下料一次的时间为定值，那么为了使一个周期内RGV上下料所用的时间G（t）取得最小值，则需RGV在移动的过程中的时间取得最小值。

2  图论组合优化

设轨道的路径网络通过表示。其中V为非空点集合;i表示节点;;W为权重系数集合，对每个节点都赋有一个耗费值Wi，对图中的每条路径Eij均赋予权重Wij。图中无循环和多重弧存在，且图中除了1、2;3、4;5、6;7、8节点不能互通，每一个节点均能经过其他任意节点。其示意图如图1所示。

在此令表示任意节点m到节点n的所有路径的集合，用Ls表示路径的总耗费为各弧和各节点的耗费的总和，Ls的计算表达式如下。

當W为随机变量时，Ls也是一个随机变量。最短路径的问题即找到耗费Ls最少的路径[2]，同时这也是一个组合优化问题，即：

若使Ls最小，要求出目标函数的最优解，每个周期内的流程如图2所示。

3  模型求解

根据上述模型，利用智能算法，求解出的最优路径为：

假设在连续8h工作过程中，CNC加工没有出现障碍。建立上下料时间与各个过程的时间的函数关系。RGV加工系统作业过程中所耗费的时间为，其中表示RGV移动i个单位所消耗的时间，t4表示CNC加工完成一个一道工序所需的时间，t7、t8分别表示RGV为奇数编号和偶数编号的CNC完成一次上下料所需时间，t9表示清洗的时间。

在上述最优路径的一个周期中，建立的函数关系式如下。

（1）当RGV按照模拟得出的最优路径进行工作，依次上料并将1号CNC换料并清洗完毕时，所需时间大于等于8号CNC加工完成时间的函数关系如下所示。

（2）当RGV按照模拟得出的最优路径进行依次上料并将1号CNC换料并清洗完毕时，所需时间大于8号CNC加工完成时间，此时对于Tuλ没有影响，而对Tdλ+1则会产生影响。影响后的Tdλ+1如下所示：

4  结语

本文以RGV小车工作效率最高为目标，使用动态调度模型得到了最优的路径。其中用到的最短路径模型，国内外许多文章都对路径网络的拓扑结构节点重要性和量度进行了论述。这类模型使用非常广泛，可以推广到现实生活中，在通信网络和最小路径规划方面都有广泛的应用。模型中分析问题、解决问题用到的一些独特的方法，对其他数学问题仍然适用。

参考文献

[1] 申鸿烨，于维海.进程先来先服务调度算法的动态演示研究[J].现代计算机：专业版，2017（22）：3-5.

[2] 张水舰，刘学军，杨洋.动态随机最短路径算法研究[J].物理学报，2012，61（16）：1-10.