基于ICEM-CFD的中子学力学耦合程序研制

袁宝新，郑杰，杨万奎，曾和荣



基于ICEM-CFD的中子学力学耦合程序研制

袁宝新，郑杰，杨万奎，曾和荣

（中国工程物理研究院 核物理与化学研究所，四川 绵阳 621900）

针对反应堆工程分析中面临的中子学力学耦合这一问题，在同一软件框架下实现中子学力学多物理场计算。利用商业CAD前处理软件ICEM-CFD对堆芯几何进行网格剖分，开发基于有限元方法的中子学力学耦合计算程序，对同一堆芯网格划分进行中子学和力学计算。初步实现了基于同一软件框架下网格层面的中子学力学耦合计算，得到了中子学力学初步耦合的计算结果。通过基准例题对程序进行计算校验，该耦合程序计算能力是可信的。

ICEM-CFD；中子学；力学；耦合；程序

有限元方法因具有非结构网格剖分能力可以适应任意几何形状，因而从20世纪60年代起逐渐在中子学计算领域得到应用和推广。国内已开发了如3DFEMJS、TFEM-2D、FEM2D-655等程序[1-4]，国外则有FEM3DJAR、FENDER、FELICIT、FELTRAN等程序[5-6]。这些程序大多采用手工方式进行几何剖分，这就使得这一时代有限元程序的几何处理模块不可避免地具有网格处理繁复及无通用性等劣势。

为开展堆内部件振动条件下堆芯核噪声频谱特性研究，需要开发一套复杂几何下的中子学力学耦合计算程序。在这个背景下，利用商业CAD前处置软件ICEM-CFD，对三维堆芯几何做四面体或六面体网格剖分，对二维堆芯几何做三角形或四边形网格剖分，开发了基于ICEM-CFD前处理器的中子学力学耦合计算程序FEMN_Couple，可以方便地获得复杂堆芯几何内细致的中子噪声频谱。

1 基本方程

1.1 中子学有限元方程

对三维中子瞬态方程做一阶微扰和傅里叶变换，并进行有限元处理[7-13]。

离散快群实部方程：

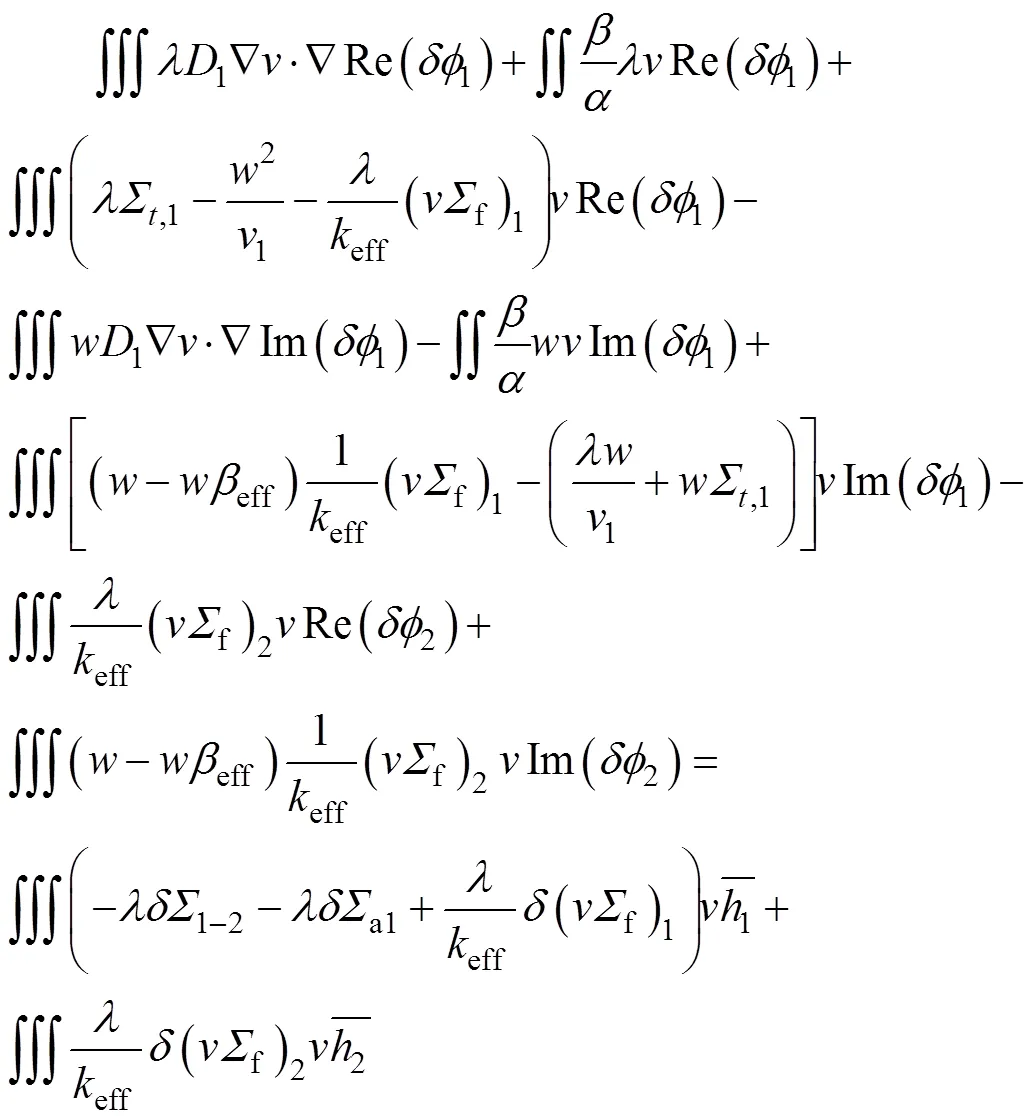
离散快群虚部方程：

离散热群实部方程：

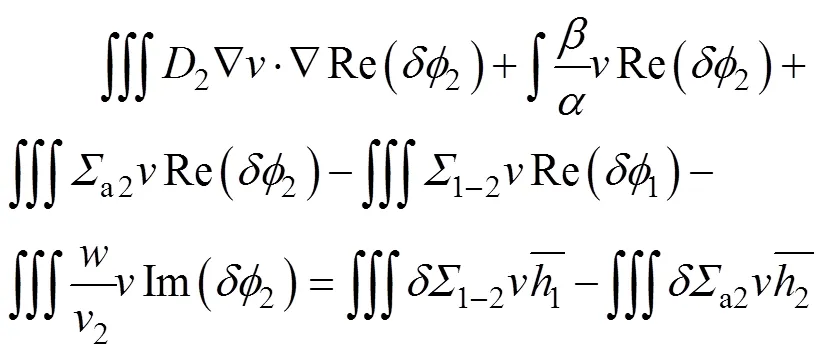
离散热群虚部方程：

1.2 振动力学有限元方程

构建结构动力学的有限元方程[14]：

对于一个悬臂梁，不计其轴向位移，其模态有限元方程为：

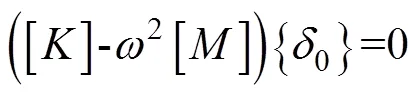
特征方程为：

2 ICEM-CFD接口技术

目前ICEM-CFD的网格输出支持Abaqus/ANSYS/ AUTODYN/LS-Dyna等格式，通过对比这些输出网格文件的格式，选用LS-Dyna网格文件格式开发FEMN_Couple程序几何模块。

1）三维计算中，LS-Dyna网格文件将网格分为固体网格（相当于体网格）和壳网格（相当于面网格）。中子学力学耦合三维计算的体网格需求为三棱柱和四棱柱，面网格需求为三角形和四边形。二维计算中，LS-Dyna网格文件将网格分为壳网格（相当于面网格）和梁网格（相当于线网格），中子学力学耦合二维计算的面网格需求为三角形和四边形，线网格需求为直线。LS-Dyna网格文件的网格类型可支持方形燃料组件、六角形燃料组件、棒形燃料组件等类型的三维/二维中子学力学耦合计算。

2）中子学计算中面中子流为连续的，在三维计算中，LS-Dyna网格文件可以不输出几何体的内部面网格。在二维计算中，LS-Dyna网格文件可以不输出几何体的内部线网格。该几何处理策略有利于系数矩阵的组装。

3）LS-Dyna按part来对网格赋予材料属性，每个组件定义为一个part，赋予该组件一个与part编号对应的材料号。在几何前处理时，按材料号准备多群截面文件，程序在单元分析计算时，查询单元所属的part编号，根据该part编号查询对应的材料号，根据材料号查询多群截面文件，结合单元当前的节点参数完成矩阵系数的组装。

3 程序结构

FEMN_Couple程序的结构如图1所示，在前处理软件ICEM-CFD中，对堆芯建模或导入CAD堆芯几何模型，手工处理边界条件，并划分网格，输出网格文件。程序读入ICEM-CFD的网格输出文件，建立单元、节点的领域表和稀疏矩阵结构表，手工输入或从材料文件读取各区域的材料信息，读入多群截面和力学参数，填充并装配系数矩阵。中子学稳态参数分析部分对堆芯群中子通量和群中子伴随通量进行计算，为中子学力学耦合瞬态计算提供稳态中子学输入参数。模态分析部分对指定结构件进行模态计算，为中子学力学耦合瞬态计算提供力学输入参数。中子学力学耦合瞬态分析部分，读入中子学稳态参数分析和模态分析的计算结果，计算中子学力学耦合方程的源项，处理边界条件，求解中子学力学耦合方程，得到群中子噪声频谱，遍历各群直至完成，输出计算结果并结束。

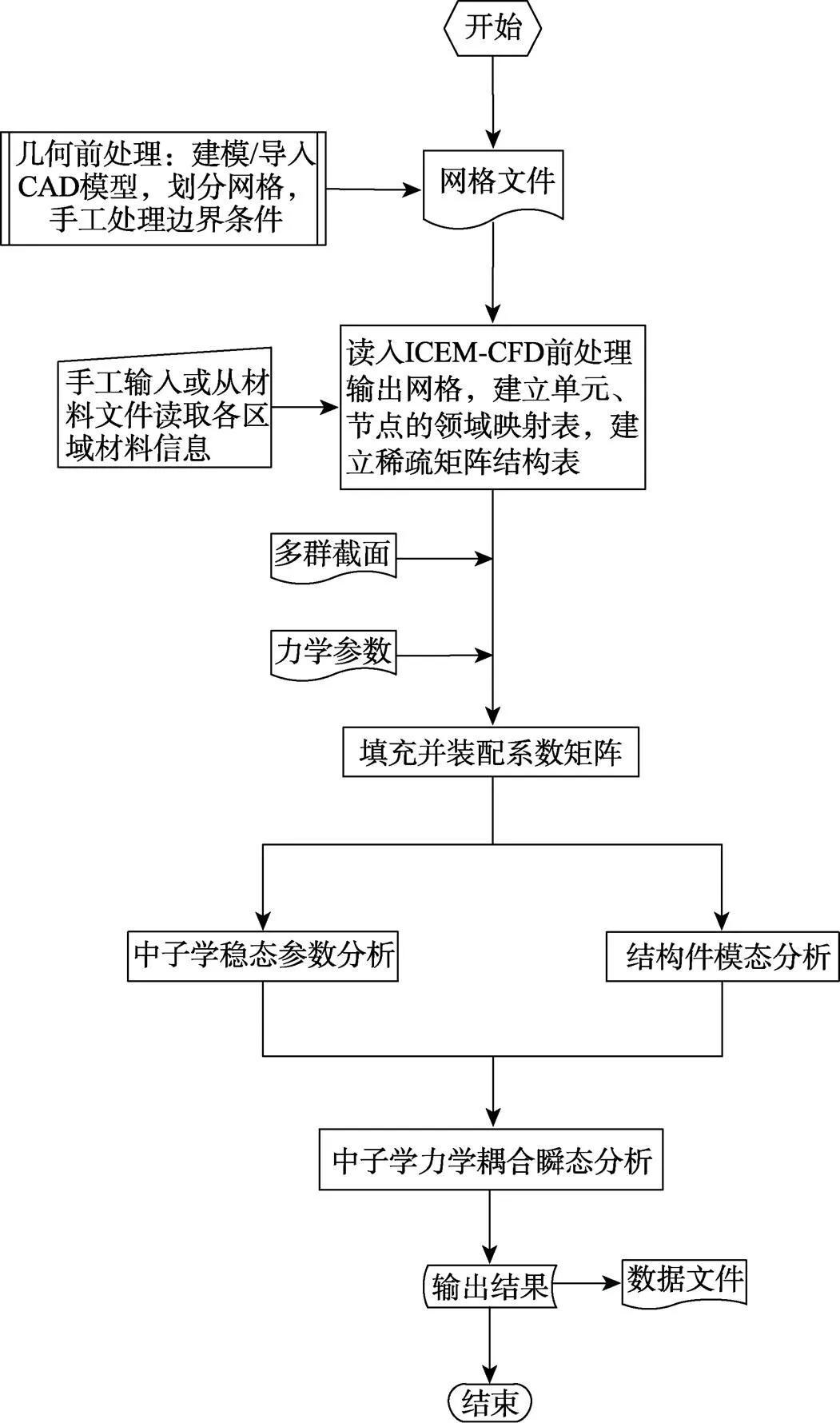
图1 程序结构

4 程序分步计算测试

4.1 中子学计算基准例题测试

选取文献[15]发布的BIBLIS例题进行中子学计算校验，该堆芯布局如图2所示，各区域材料可参考文献[15]。根据文献[16]，在坐标(195,195)、(250,195)和(310,195)处分别设置一个热群中子噪声点源，使用FEMN_Couple程序的中子学模块对该问题进行计算，得到的热群中子噪声分布如图3所示。可以看出，随着点源位置从堆芯正中心往外圈移动，热群中子噪声的波峰也随之向外圈移动，热群中子噪声波形与文献[16]计算结果基本一致。

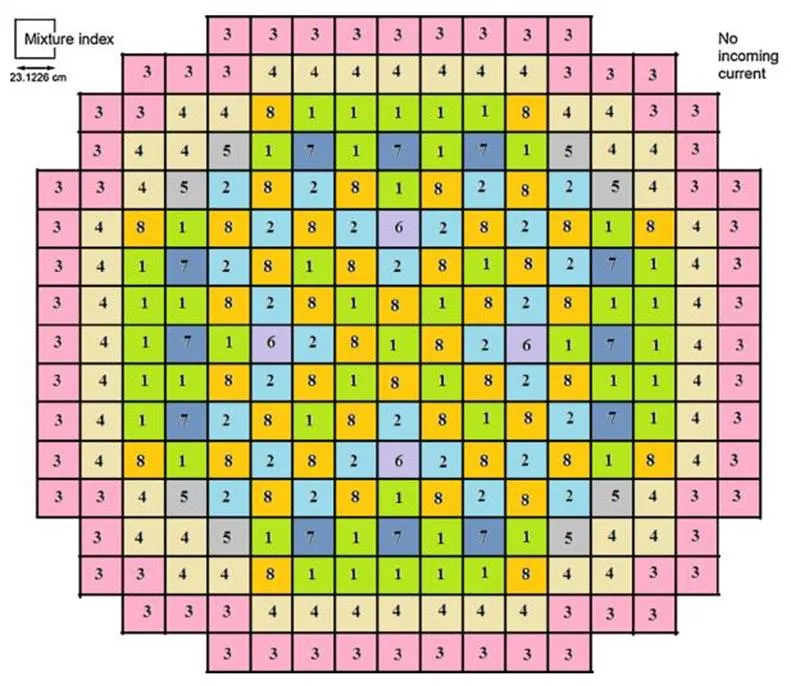
图2 BIBLIS堆芯布局

4.2 力学计算例题测试

对于固定组件，其在堆芯内部的振动可以等效为一个悬臂梁振动问题，不计其轴向位移有：

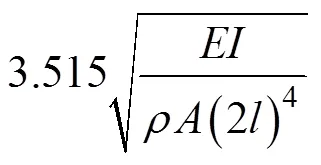
图3 源位置在不同坐标引起的热群中子噪声幅值分布

5 中子学力学耦合计算

振动情况下的吸收截面可以表示为：

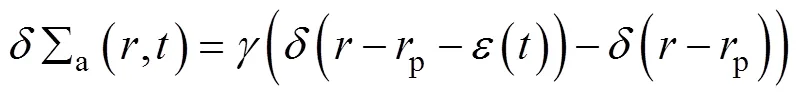
部件振动条件下的噪声表示为：

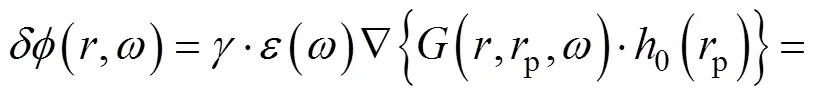
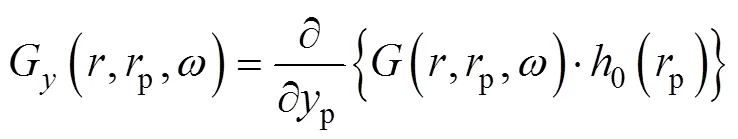
选取文献[15]发布的BIBLIS例题，将该中心组件的一阶振动频率代入上述方程，使用FEMN_ Couple程序进行中子学力学耦合计算，得到热群中子噪声实部波形如图4所示。该结果与文献[16]给出的控制棒振动情况下堆芯热群中子的实部波形分布基本一致。

图4 中心组件的一阶振动频率下的热群中子噪声实部

6 结语

针对反应堆工程分析中面临的中子学力学耦合这一问题，文中利用商业CAD前处理软件ICEM-CFD对堆芯几何进行了网格剖分，开发了基于有限元方法的中子学力学耦合计算程序FEMN_Couple，对同一堆芯网格划分进行中子学和力学计算，初步实现了基于同一软件框架下网格层面的中子学力学耦合，给出了中子学力学耦合的初步计算结果。下一步将在程序支持部件受迫振动力学计算及部件受迫振动中子学力学耦合计算两个方面进一步开展工作。

[1] 屠柱国, 汤裕仁, 黄艾香, 等. 用有限元法求解三维中子扩散方程的研究—三维中子扩散有限元程序3DFEMJS[J]. 核科学与工程, 1983, 3(2): 115-126.

[2] 顾丽珍, 王永庆, 于素花, 等. 有限元法在计算二维反应堆中子扩散方程中的应用[J]. 清华大学学报, 1980, 20(4): 97-110.

[3] 郭海兵, 刘永康, 施工. 基于CAD建模和有限元方法的三维中子扩散程序[J]. 清华大学学报, 2012, 52(7): 901-905.

[4] 薛友义. 有限元法在解中子扩散方程中的应用[J]. 核动力工程, 1981, 2(2): 10-20.

[5] YOSHITAKA N RYUJI K, YUKIO T, et al. A Computer Program for Solving the Three-dimensional Multigroup Diffusion Equation by Finite Element Method with 20-node Isoparametric Element (FEM3DJAR)[J]. Progress in Nuclear Energy, 1986, 18(1-2): 207-214.

[6] SHUTTLEWORTH E. Fender: A Finite Element Code for the Solution of the Diffusion Equation in Shield Design Applications[J]. Annals of Nuclear Energy, 1981, 8(11-12): 597-607.

[7] 刘金汇, 谷芳毓. 反应堆堆内部件振动的中子噪声物理模型[J]. 核动力工程, 1999, 20(1): 36-41.

[8] 彭钢. 反应堆堆内部件振动的中子噪声物理模型[J]. 核科学与工程, 2001, 21(3): 264-270.

[9] 彭钢. 反应堆冷却剂沸腾中子噪声物理模型研究[J]. 核动力工程, 2000, 21(5): 385-388.

[10] CHRISTOPHE D, IMRE P. Numerical Tools Applied to Power Reactor Noise analysis[J]. Progress in Nuclear Energy, 2009, 51: 67-81.

[11] VIKTOR L, CHRISTOPHE D, IMRE P et al. Neutron Noise Calculations Using the Analytical Nodal Method and Comparisons with Analytical Solutions[J]. Annals of Nuclear Energy, 2011, 38:808-816.

[12] CHRISTOPHE D. Development of a 2-D 2-group Neutron Noise Simulator[J]. Annals of Nuclear Energy, 2004, 31: 647-680.

[13] CHRISTOPHE D. Comparison of the Calculated Neutron Noise Using Finite Differences and the Analytical Nodal Method[J]. Annals of Nuclear Energy, 2012, 43: 176-182.

[14] 张相庭, 王志培, 黄本才, 等. 结构振动力学[M]. 上海: 同济大学出版社, 2005.

[15] SEYED A H, FARAHNAZ S D. Galerkin and Generalized Least Squares Finite Element: A Comparativestudy for Multi-group Diffusion Solvers[J]. Progress in Nuclear Energy, 2015, 85: 473-490.

[16] SEYED A H, NASER V. Neutron Noise Simulation by GFEM and Unstructured Triangle Elements[J]. Nuclear Engineering and Design, 2012, 253: 238-258.

Research on Coupling Code of ICEM-CFD Based Neutronic and Mechanics

YUAN Bao-xin, ZHENG Jie, YANG Wan-kui, ZENG He-rong

(Institute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang 621900, China)

In view of the neutronic and mechanical coupling problems in reactor engineering analysis, to realize the multi physics field calculation under the same software framework.The CAD pre-processing software ICEM-CFD was used to carry out mesh subdivision of core geometry to develop neutron computation module and the mechanical calculation module based on the finite element method, and execute neutronic and mechanical calculations for the same mesh subdivision of core geometry.It preliminary realized mechanical coupled neutronics calculation of mesh based on the software framework and obtained the calculation results of preliminary neutronics mechanics coupling.Calculation and verification of code based on benchmark examples shows that the code for calculating the capacity can be trusted.

ICEM-CFD; neutronic; mechanics; coupling; code

10.7643/ issn.1672-9242.2019.02.007

TL329

A

1672-9242(2019)02-0032-05

2018-11-22；

2018-12-18

国家自然科学基金面上项目（11475150）；四川省科技计划项目（2018JY0622）。

袁宝新（1988—），男，湖北黄冈人，硕士研究生，主要研究方向为反应堆物理。