基于时间序列模型的降雨量预测分析
2019-03-07张耀文姜纪沂赵振宏
程 敏,张耀文,姜纪沂*,任 杰,赵振宏
(1.防灾科技学院,北京101601;2.中国地质调查局西安地质调查中心,西安710054)
降雨量的短期变化,往往会造成严重的干旱涝、洪灾害,并对当地经济发展等造成不同程度的影响。高精度的降雨量预测方法能及早地发现降雨量变化情况,提高应对此类灾害的能力[1]。降雨量是衡量干旱程度的一个重要指标,直接反映了自然界的变化,降雨量的大小直接影响农业生产[2]。如能对降雨量做出科学准确预测,农业、水利等有关部门就可以及时采取防涝抗旱措施[3],降低不必要的损失,因此降雨量预测已成为当前预测中的重要研究课题[4]。对于水资源短缺的北方来说,地下水是北方的主要用水来源,高精度的预测降雨量,能最大限度的利用水资源,将多余的水储存起来,以缓解水资源短缺问题,降低因水资源短缺或极度缺少而带来的经济损失。
基于这种情况,本文试图运用时间序列中的ARIMA模型对该地区的降雨量进行预测,进而了解未来5年内济南市的降雨量变化情况。
1 研究区概况与预测方法
济南市坐落于鲁西北冲积平原和鲁中低山丘陵的接触地带,北部为黄河下游平原,南部为泰山山系,地势北部低、南部高,平原稍微倾向东北,黄河沿西南—东北方向穿过济南市所在的区域,黄河河床高出地面形成地上河,在黄两岸发育有诸多的呈条带状的洼地。最高峰为南部西营镇梯子山,地面标高975.8m,如图1。

图1 济南市水系分布
某种统计指标的数值按时间先后顺序排列所形成的数列叫做时间序列[5]。时间序列模型主要分为两类,一是ARMA(Auto Regression Moving Average)模型,即自回归移动平均模型[6];二是ARIMA(Auto Regressive Integrated Moving Average Model)模型,即自回归积分滑动平均模型[7]。其实两类模型可以看做是两类模型的组合再加上差分运算,一类模型是AR; 一类模型是MA,ARMA模型可以看做是AR+MA;而ARIMA可以看做是AR+差分处理+MA。
在ARIMA(p,d,q)模型进行预测时,所用序列必须是平稳的序列,如果是非平稳化的序列,就需将其转化为平稳化的序列[8]。
2 研究区数据及处理
以济南市1959~2010年降雨量数据作为本次分析样本,在SPSS的预测选项中创建ARIMA模型,并进行向前预测,使用2011~2015年降雨量数据检验ARIMA模型的预测准确度,如图2。

图2 1959~2010年降雨量序列
在SPSS软件平台进行降雨量的输入与定义日期,然后进行数据序列图的绘制[9],如图3。
从图3可看出,该时间序列在1967,1985,2003年具有较大波动,但总体具有一定的向下趋势,并不平稳。需要对1959~2010年的降雨量数据进行平稳化处理。

图3 降雨量平稳化序列
在SPSS软件中绘制的降雨量一阶差分的自相关图和偏自相关图如图4。可以看出,一阶差分后数据序列的自相关系数在显著不为0后趋于0,而一阶差分后的偏自相关系数较接近0。判定数据序列基本平稳。故ARIMA模型参数d取值为1。

图4 自相关图和偏自相关图
根据自相关图和偏自相关图均表现为拖尾现象适用于ARMA模型,从偏自相关图中可见在5%的显著水平下,偏自相关系数显著不为0的个数为3,之后趋于0,并呈现拖尾现象,故判断p值取3或2(取2主要是因为最后一个显著超过0的阶数是由于偶然出现的,确定p值时需要剔出); 从自相关图中可看出在5%的显著水平下,自相关系数显著为零的个数为6,故判断q值取6或5(取5主要是最后一个显著超过0的系数是由于偶然出现的,确定p值时需要剔出)。利用SPSS建立ARIMA模型,经过前期的预测对比分析,根据SPSS中输出的模型统计量表格中的BlC值确定最佳模型。一般来讲,选取BIC达到最小的模型为最佳模型。
经过前期数据处理与分析,模型可初定为ARIMA (3,1,6)、ARIMA (3,1,5)、ARIMA (2,1,6)ARIMA(2,1,5)。用SPSS软件作拟合图比较4种模型拟合(如图5),检验选择模型的准确性。根据BIC定阶准则选出最优模型,如表1。可知模型ARIMA(2,1,5)BIC值最小,其值为11.654。
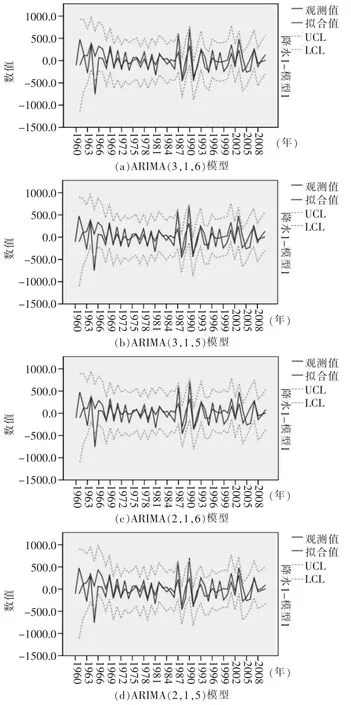
图5 4种模型拟合

表1 4种模型BIC比较
由于预测准确度分析的年份为2011~2015年,ARIMA(2,1,5)的预测趋势跟观察值的走势基本一致,而其他3个模型的预测趋势都偏离了观察值的走势,所以ARIMA (2,1,5)的拟合效果最好。同时,ARIMA(2,1,5)模型的BIC值最小,可选取此模型作为最后的预测模型。
对残差序列进行白噪声检验,根据SPSS中输出的模型统计量表来看,ARIMA(2,l,5)模型的Ljung-Box统计量Q=7.734。p值为0.737显著大于0.05的检验水平,即接受Ljung-Box的原假设:所有数据之间相互独立,可认为残差序列为白噪声序列[9]。
模型残差序列的自相关系数与偏自相关系数的分布在以0为中心的范围内,并且自相关系数与偏自相关系数的绝对值均小于0.3(如图6),认为此残差序列之间是相互独立的,意味着残差序列是白噪声的。模型涵盖了所有的信息,说明此模型效果较好。

图6 残差序列自相关和偏自相关
综上,ARIMA(2,1,5)符合BIC准则,通过了拟合度检验与白噪声检验,因此可以用ARIMA(2,1,5)对降雨量进行预测。表明济南市2010~2015年降雨量预测同样适用ARIMA(2,1,5)预测。
3 预测结果与分析
本次选择了ARIMA(2,1,5),利用济南市1959~2010年的降雨量数据,对该地区2011~2015年的降雨量进行预测,如表2、表3、表4。
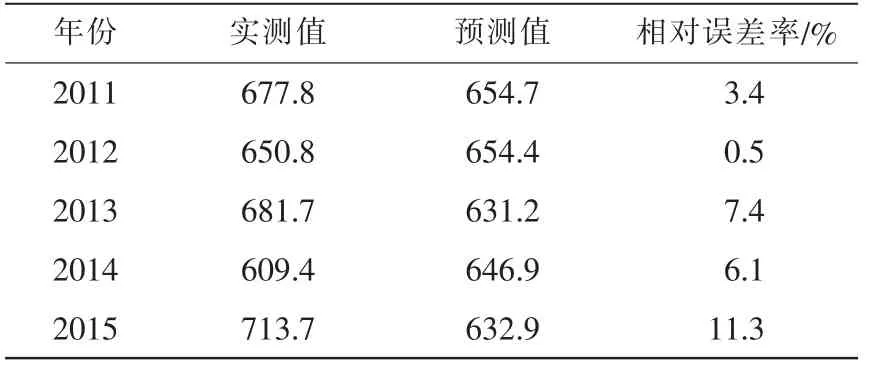
表2 ARIMA预测值与实际值统计 单位:mm

表3 ARIMA预测值与实际值统计 单位:mm

表4 ARIMA的预测值与实际值统计 单位:mm
从表2、表3和表4看出,ARIMA模型预测年限为4年。表2中2011~2015年的平均相对误差为5.74%,预测精度控制在10%以内;2014年以后,预测精度大于10%。表3中2010~2015年平均相对误差4.9%,预测精度控制在10%以内;2015年预测精度大于10%。表4中2010~2013年平均相对误差为2.2%,预测精度控制在10%以内,其中2010年和2013年的预测精度为1.0%,逼近实际观测值,预报准确。由此推测,ARIMA模型对降雨量的预测在连续的4~5年内对降雨量的预测非常准确。
同样方法,在SPSS软件分析预测选项中对2016~2020年降雨量进行预测,如表5。

表5 2016~2020年降雨量预测值 单位:mm
2016~2020年济南市的降雨量较平稳,波动较小,大多分布在济南市的平均降雨量672.8mm周围。预测结果看出,济南市2016~2020年不会发生较大洪水,但ARIMA模型预测降雨量不一定准确,因降雨量受较多因素影响,仅凭时间序列是不能完全准确的预测降雨量。
通过模型确定,综合1959~2015年的降雨量数据,时间序列,如图7。从图7可看出,1959~1991年30多年内,这段时期内降雨量波动较大,而1992~2015年,这段时期内降雨量波动较小;从大趋势来看,济南市降雨量逐渐减少。
2016~2020年降雨量进行预测,结果表明,这5年济南市降雨量波动较小,大多在650mm上下波动,预计接未来5年没有大的旱灾和洪灾。

图7 1959~2015年降雨量序列
从原理来看,ARIMA模型具有一定的数理统计意义,即ARIMA模型具有偶然性,且这种偶然性会随着预测时间长短变化而变化,可能会随着时限增加而这种偶然性出现的频率增加,同时也有可能随着预测时限的缩短而增长(预测时限越短,其预测准确度会有一定提高)。
4 结语
(1)用ARIMA模型对济南市未来5年的年降雨量进行预测,其结果显示未来5年的年平均降雨量为659.2mm,这 与1959~2015年的多年平均降雨量672.8mm较为接近,说明济南市未来5年出现干旱及洪涝灾害的可能性较小。
(2)济南市降雨量的变化呈现出一个逐渐减小的趋势,说明济南市地下水的大气降雨补给量将会出现下降趋势,需要更加合理地利用和分配水资源。
(3)由于影响一个地区降雨量的因素很多,诸如地区纬度的差异,气温变化、所处地理位置、生态环境的因素(植被的覆盖率,流域的分布状况)[10],以及人为影响因素等,所以只用时间序列分析方法来预测降雨量的效果较差,需考虑多方面的因素,综合现有的预测模型,建立适合当地的降雨量预测模型,从而使得降雨量预测更为可靠。
